人工神经网络（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：人工神经网络是一个互相连接的节点群，灵感来源于大脑中神经元的简化模型。在这里，每个圆形节点代表一个人工神经元，箭头代表从一个人工神经元的输出到另一个人工神经元输入的连接。

　　 在机器学习中，神经网络（也称为人工神经网络或神经网，缩写为 ANN 或 NN）是一种受到动物大脑生物神经网络结构和功能启发的模型。[1][2]

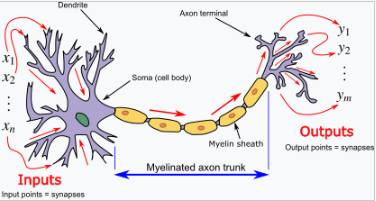
　　 一个人工神经网络由连接的单元或节点组成，这些节点被称为人工神经元，粗略地模拟大脑中的神经元。这些神经元通过边（连接）相互连接，模拟大脑中的突触。每个人工神经元接收来自连接神经元的信号，然后处理这些信号并将结果传送给其他连接的神经元。这个 “信号” 是一个实数，每个神经元的输出通过某个非线性函数计算，该函数作用于输入的和，这个过程被称为激活函数。每个连接的信号强度由一个权重决定，权重会在学习过程中调整。

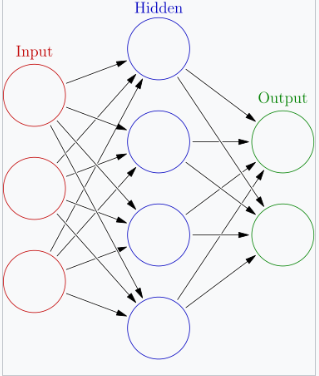
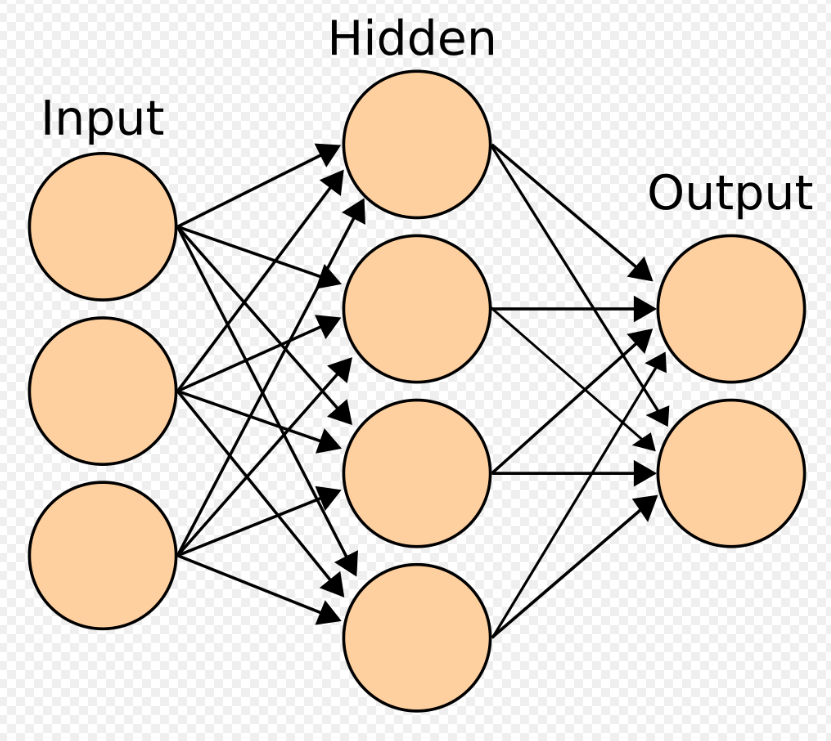
　　 通常，神经元会被聚合成层。不同的层可能对其输入执行不同的变换。信号从第一层（输入层）传输到最后一层（输出层），可能会经过多个中间层（隐藏层）。如果一个网络至少有两个隐藏层，通常称其为深度神经网络。[3]

　　 人工神经网络被用于各种任务，包括预测建模、自适应控制和解决人工智能中的问题。它们能够从经验中学习，并能够从复杂且看似不相关的信息集中推导结论。

1. 训练

　　 神经网络通常通过经验风险最小化进行训练。这种方法基于优化网络参数，以最小化预测输出与给定数据集中的实际目标值之间的差异或经验风险的理念。[4] 基于梯度的方法，如反向传播，通常用于估计网络的参数。[4] 在训练阶段，人工神经网络通过标记的训练数据进行学习，通过迭代更新参数以最小化定义的损失函数。[5] 这种方法使得网络能够对未见过的数据进行泛化。

2. 历史

早期工作

　　 今天的深度神经网络基于 200 多年前统计学的早期工作。最简单的前馈神经网络（FNN）是一个线性网络，它由一层输出节点组成，节点使用线性激活函数；输入通过一系列权重直接馈送到输出。在每个节点上，输入和权重的乘积之和会被计算出来。通过对这些计算的输出与给定目标值之间的均方误差进行最小化，调整权重。这种技术已经有两个多世纪的历史，被称为最小二乘法或线性回归。它由勒让德（1805 年）和高斯（1795 年）用于预测行星运动，通过找到一组点的最佳线性拟合。[7][8][9][10][11]

　　 历史上，像冯·诺依曼模型这样的数字计算机通过执行显式指令并通过多个处理器访问内存来操作。另一方面，一些神经网络起源于试图通过联结主义框架模拟生物系统中的信息处理。与冯·诺依曼模型不同，联结主义计算不将内存和处理分开。

　　 沃伦·麦卡洛克和沃尔特·皮茨（1943 年）考虑了一个非学习型的神经网络计算模型。[13] 这个模型为神经网络研究分裂成两种不同的方向奠定了基础。一种方向专注于生物过程，而另一种方向则专注于神经网络在人工智能中的应用。

　　 在 20 世纪 40 年代末，D.O. Hebb[14] 提出了一个基于神经可塑性机制的学习假设，这个假设后来被称为赫布学习（Hebbian learning）。它被用于许多早期的神经网络中，例如 Rosenblatt 的感知器和霍普菲尔德网络。Farley 和 Clark[15]（1954 年）使用计算机模拟了一个赫布网络。其他神经网络计算机器由 Rochester、Holland、Habit 和 Duda（1956 年）创建。[16]

　　 1958 年，心理学家 Frank Rosenblatt 描述了感知器，这是一种最早实现的人工神经网络之一，[17][18][19][20] 由美国海军研究办公室资助。[21] R.D. Joseph（1960 年）[22] 提到 Farley 和 Clark（1956 年）开发的早期感知器类设备：[10] "麻省理工学院林肯实验室的 Farley 和 Clark 实际上在感知器类设备的开发上先于 Rosenblatt。" 然而，他们 “放弃了这个课题。” 感知器引发了公众对人工神经网络研究的热情，促使美国政府大幅增加资金。这为计算机科学家对感知器能够模拟人类智能的乐观预期提供了支持，进一步推动了 “人工智能的黄金时代”。[23]

　　 最初的感知器没有自适应的隐藏单元。然而，Joseph（1960 年）[22] 也讨论了具有自适应隐藏层的多层感知器。Rosenblatt（1962 年）[24]: 第 16 节 引用并采纳了这些想法，同时也给出了 H.D. Block 和 B.W. Knight 的工作。然而，这些早期的努力并未导致隐藏单元的有效学习算法，也就是深度学习的实现未能成功。

1960 年代和 1970 年代的深度学习突破

　　 在 1960 年代和 1970 年代，人工神经网络（ANNs）进行了基础研究。第一个有效的深度学习算法是数据处理组方法（Group Method of Data Handling），这是一个用于训练任意深度神经网络的方法，由 Alexey Ivakhnenko 和 Lapa 于苏联（1965 年）提出。他们将其视为一种多项式回归方法，[25] 或者说是 Rosenblatt 感知器的推广。[26] 1971 年的一篇论文描述了一个由这种方法训练的八层深度网络，[27] 该方法基于通过回归分析逐层训练的方式。通过使用单独的验证集修剪冗余的隐藏单元。由于节点的激活函数是 Kolmogorov-Gabor 多项式，这些也成为了第一个具有乘法单元或 “门” 的深度网络。[10]

　　 第一个通过随机梯度下降（SGD）训练的深度学习多层感知器（MLP）由 Shun'ichi Amari 于 1967 年发布。[29] 在 Amari 的学生 Saito 进行的计算机实验中，一个具有五层的多层感知器（MLP）通过修改两层的方式学习了内部表示，用于对非线性可分模式类别进行分类。[10] 随着硬件和超参数调优的发展，端到端的随机梯度下降目前已成为主流的训练技术。

　　 1969 年，Kunihiko Fukushima 引入了 ReLU（修正线性单元）激活函数。[10][30][31] 修正器成为了深度学习中最流行的激活函数。[32]

　　 尽管如此，在美国的研究在 Minsky 和 Papert（1969 年）的工作之后停滞不前，[33] 他们强调基础感知器无法处理异或（exclusive-or）电路。这个洞察对 Ivakhnenko（1965 年）和 Amari（1967 年）的深度网络并不适用。

　　 1976 年，迁移学习在神经网络学习中被引入。[34][35]

　　 深度学习架构用于卷积神经网络（CNNs），包括卷积层、降采样层和权重复制，始于 Kunihiko Fukushima 于 1979 年引入的 Neocognitron，尽管该网络并未通过反向传播进行训练。[36][37][38]

反向传播

　　 反向传播是一种有效的链式法则应用，由戈特弗里德·威廉·莱布尼茨（Gottfried Wilhelm Leibniz）于 1673 年提出[39]，用于可微节点的网络。术语 “反向传播误差” 最早是由 Rosenblatt 在 1962 年提出的，[24] 但当时他并不知道如何实现这一过程，尽管亨利·J·凯利（Henry J. Kelley）在 1960 年在控制理论的背景下已经有了反向传播的连续先驱[40]。1970 年，塞波·林奈马（Seppo Linnainmaa）在他的硕士论文中发表了现代形式的反向传播（1970 年）[41][42][10]。G.M. 奥斯特罗夫斯基（G.M. Ostrovski）等人在 1971 年重新发表了这一工作[43][44]。保罗·韦尔博斯（Paul Werbos）在 1982 年将反向传播应用于神经网络[45][46]（他的 1974 年博士论文，1994 年再版的书籍[47]中并未描述该算法[44]）。1986 年，大卫·E·鲁梅哈特（David E. Rumelhart）等人普及了反向传播，但没有引用原始的工作[48]。

卷积神经网络

　　 1979 年，福岛邦彦（Kunihiko Fukushima）提出的卷积神经网络（CNN）架构[36]，同时引入了最大池化（max pooling）[49]，这一程序成为 CNN 中常用的下采样方法。卷积神经网络（CNN）已成为计算机视觉领域的重要工具。

　　 时延神经网络（TDNN）由亚历克斯·韦博尔（Alex Waibel）于 1987 年提出，旨在将 CNN 应用于音素识别。它使用了卷积、权重共享和反向传播技术[50][51]。1988 年，张伟（Wei Zhang）将一个经过反向传播训练的 CNN 应用于字母识别[52]。1989 年，扬·勒昆（Yann LeCun）等人创建了一个名为 LeNet 的 CNN，用于识别邮寄物品上的手写邮政编码。训练过程耗时 3 天[53]。1990 年，张伟将 CNN 实现于光学计算硬件上[54]。1991 年，CNN 被应用于医学影像中的物体分割[55]以及乳腺癌的乳腺 X 光检测[56]。LeNet-5（1998），由扬·勒昆等人提出的一个 7 层 CNN，用于对数字进行分类，被几家银行应用于识别支票上手写的数字，数字图像为 32×32 像素[57]。

　　 自 1988 年起[58][59]，神经网络的使用在蛋白质结构预测领域带来了变革，尤其是在第一个级联网络通过多重序列比对生成的轮廓（矩阵）进行训练时[60]。

循环神经网络

　　 RNN（循环神经网络）的一个起源是统计力学。1972 年，天野俊一（Shun'ichi Amari）提出通过 Hebbian 学习规则修改 Ising 模型的权重，作为联想记忆的模型，并加入了学习的成分[61]。这一概念由约翰·霍普菲尔德（John Hopfield）于 1982 年推广为霍普菲尔德网络[62]。RNN 的另一个起源是神经科学。术语 “recurrent”（循环）用于描述解剖学中的环路结构。1901 年，卡哈尔（Cajal）在小脑皮层观察到 “循环半圆形” 结构[63]。赫布（Hebb）则将 “回响电路” 作为短期记忆的解释[64]。麦卡洛克和皮茨（McCulloch and Pitts，1943）在论文中考虑了包含循环的神经网络，并指出此类网络的当前活动可以受到远古历史中活动的影响[12]。

　　 1982 年，提出了一种名为**Crossbar Adaptive Array**的循环神经网络（而非多层感知器结构），其使用了从输出到监督（教师）输入的直接递归连接。除了计算行动（决策），它还计算了结果情境的内部状态评估（情感）。通过消除外部监督，该网络引入了神经网络中的自我学习方法。

　　 在 1980 年代初期的认知心理学期刊《American Psychologist》中，开展了一场关于认知与情感之间关系的辩论。1980 年，扎琼茨（Zajonc）表示情感是首先计算的，并且独立于认知，而拉扎鲁斯（Lazarus）则在 1982 年指出，认知是首先计算的，并且与情感不可分离[67][68]。1982 年，Crossbar Adaptive Array 提出了一种神经网络模型来说明认知-情感关系[65][69]。这是人工智能系统——一种循环神经网络——在认知心理学领域所贡献的一个例子。

　　 两项早期有影响力的工作是乔丹网络（Jordan Network，1986）和埃尔曼网络（Elman Network，1990），它们应用 RNN 研究认知心理学。

　　 在 1980 年代，反向传播算法在深层 RNN 上表现不佳。为了克服这一问题，1991 年，Jürgen Schmidhuber 提出了 “神经序列分块器”（neural sequence chunker）或 “神经历史压缩器”（neural history compressor）[70][71]，该方法引入了自我监督预训练（ChatGPT 中的 “P”）和神经知识蒸馏的重要概念[10]。1993 年，一个神经历史压缩系统解决了一个需要超过 1000 层递归展开的 “非常深的学习” 任务[72]。

　　 1991 年，Sepp Hochreiter 的学位论文[73]识别并分析了梯度消失问题[73][74]，并提出了递归残差连接来解决该问题。他与 Schmidhuber 一起提出了长短期记忆（LSTM），在多个应用领域创造了准确度记录[75][76]。但这还不是现代版本的 LSTM，现代 LSTM 需要遗忘门（forget gate），该门在 1999 年被引入[77]。它成为了 RNN 架构的默认选择。

　　 在 1985 到 1995 年间，受到统计力学启发，Terry Sejnowski、Peter Dayan、Geoffrey Hinton 等人开发了多个架构和方法，包括 Boltzmann 机[78]、限制玻尔兹曼机[79]、赫尔姆霍兹机[80]和唤醒-睡眠算法[81]。这些方法设计用于深度生成模型的无监督学习。

深度学习

　　 在 2009 到 2012 年间，人工神经网络（ANN）开始在图像识别竞赛中获奖，并在各种任务上接近人类水平的表现，最初是在模式识别和手写识别方面[82][83]。2011 年，Dan Ciresan、Ueli Meier、Jonathan Masci、Luca Maria Gambardella 和 Jürgen Schmidhuber 团队提出的 CNN 模型 DanNet[84][85]首次在视觉模式识别竞赛中取得超人类表现，超越传统方法三倍[38]。随后它继续赢得了更多竞赛[86][87]。他们还展示了在 GPU 上使用最大池化 CNN 显著提高了性能[88]。

　　 2012 年 10 月，Alex Krizhevsky、Ilya Sutskever 和 Geoffrey Hinton 提出的 AlexNet[89]在 ImageNet 大型竞赛中以显著的优势战胜了浅层机器学习方法。随后的增量改进包括 Karen Simonyan 和 Andrew Zisserman 提出的 VGG-16 网络[90]以及 Google 的 Inceptionv3[91]。

　　 2012 年，吴恩达（Ng）和 Dean 创造了一个网络，仅通过观看无标签图像，便学习识别更高层次的概念，例如猫[92]。无监督预训练和来自 GPU 和分布式计算的计算能力提升，使得能够使用更大的网络，特别是在图像和视觉识别问题中，这被称为 “深度学习”[5]。

　　 2013 年，径向基函数和小波网络被引入。这些网络展示了最佳逼近性质，并已应用于非线性系统识别和分类问题[93]。

　　 生成对抗网络（GAN）（Ian Goodfellow 等人，2014）[94]在 2014 到 2018 年期间成为生成建模领域的技术前沿。GAN 原理最早由 Jürgen Schmidhuber 于 1991 年提出，他称之为 “人工好奇心”：两个神经网络通过零和博弈的形式相互竞争，其中一个网络的获益是另一个网络的损失[95][96]。第一个网络是生成模型，它建模输出模式的概率分布。第二个网络通过梯度下降学习预测环境对这些模式的反应。Nvidia 的 StyleGAN（2018）[97]基于 Tero Karras 等人提出的 Progressive GAN[98]，成功实现了优质图像生成。这里，GAN 生成器以金字塔的形式从小到大逐步增长。GAN 的图像生成取得了广泛成功，并引发了关于深度伪造（deepfakes）的讨论[99]。自此以来，扩散模型（2015）[100]在生成建模中超越了 GAN，出现了 DALL·E 2（2022）和 Stable Diffusion（2022）等系统。

　　 2014 年，技术前沿是训练具有 20 到 30 层的 “非常深的神经网络”[101]。堆叠过多的层导致训练准确度急剧下降[102]，即 “退化” 问题[103]。2015 年，提出了两种训练非常深网络的技术：高速公路网络（highway network）在 2015 年 5 月发布[104]，残差神经网络（ResNet）在 2015 年 12 月发布[105][106]。ResNet 类似于开门的高速公路网络。

　　 在 2010 年代，seq2seq 模型被开发出来，并加入了注意力机制。2017 年，这导致了现代 Transformer 架构的提出，详见论文《Attention Is All You Need》[107]。Transformer 的计算时间与上下文窗口的大小成二次方关系。Jürgen Schmidhuber 的快速权重控制器（1992）[108]是线性增长的，后来证明其等价于未经归一化的线性 Transformer[109][110][10]。Transformer 已逐渐成为自然语言处理的首选模型[111]。许多现代大型语言模型，如 ChatGPT、GPT-4 和 BERT，都采用了这一架构。

3. 模型

图
图 2：神经元和有髓轴突，信号从树突的输入流向轴突末端的输出

　　 人工神经网络（ANN）最初是试图利用人脑的结构来执行传统算法难以成功的任务。很快，它们开始重新定位，专注于提高经验结果，放弃了保持忠于生物学原型的尝试。人工神经网络能够学习并建模非线性和复杂的关系。这是通过神经元之间以各种模式连接实现的，允许某些神经元的输出成为其他神经元的输入。网络形成了一个有向加权图[112]。

　　 人工神经网络由模拟神经元组成。每个神经元通过类似生物轴突-突触-树突连接的链接与其他节点相连。所有通过链接连接的节点接收一些数据，并利用这些数据执行特定的操作和任务。每个链接都有一个权重，决定了一个节点对另一个节点的影响力[113]，通过调整权重来选择神经元之间的信号传递。

人工神经元

　　 人工神经网络（ANNs）由人工神经元组成，概念上源自生物神经元。每个人工神经元有输入并生成一个输出，这个输出可以传递给多个其他神经元。[114] 输入可以是外部数据样本的特征值，例如图像或文档，也可以是其他神经元的输出。神经网络的最终输出神经元的输出完成任务，例如识别图像中的物体。[citation needed]

　　 为了找到神经元的输出，我们将所有输入的加权和相加，加权由从输入到神经元的连接的权重决定。我们还会在这个和上加上一个偏置项。[115] 这个加权和有时称为激活值。然后，这个加权和通过一个（通常是非线性的）激活函数来生成输出。初始输入是外部数据，例如图像和文档。最终的输出完成任务，例如识别图像中的物体。[116]

组织结构

　　 神经元通常被组织成多个层次，特别是在深度学习中。一个层次的神经元只与紧接其前后层的神经元相连接。接收外部数据的层是输入层。产生最终结果的层是输出层。它们之间可能有零个或多个隐藏层。也有使用单层和无层网络的情况。在两层之间，可能有多种连接模式。它们可以是‘全连接’的，即一个层的每个神经元都与下一个层的每个神经元相连。也可以是池化层，其中一个层中的一组神经元连接到下一个层中的一个神经元，从而减少该层中神经元的数量。[117] 只有这种连接的神经元形成一个有向无环图（DAG），并且被称为前馈网络。[118] 另一种选择是，允许层内或前一层的神经元之间的连接的网络，称为递归网络。[119]

超参数

　　 超参数是一个常数参数，其值在学习过程开始之前就已设定。参数的值是通过学习过程得到的。超参数的例子包括学习率、隐藏层的数量和批量大小。[citation needed] 一些超参数的值可能依赖于其他超参数的值。例如，某些层的大小可能依赖于整体层数。

学习

　　 学习是通过考虑样本观察结果，使网络更好地处理任务的适应过程。学习涉及调整网络的权重（和可选的阈值），以提高结果的准确性。这是通过最小化观察到的错误来完成的。当额外观察结果无法有效减少错误率时，学习就完成了。即使在学习后，错误率通常也不会达到 0。如果学习后错误率过高，通常需要重新设计网络。实际操作中，通过定义一个在学习过程中定期评估的代价函数来完成这一过程。只要代价函数的输出继续下降，学习就会继续进行。代价通常定义为一个只能近似计算的统计量。输出实际上是数字，因此当错误较低时，输出（几乎可以确定是猫）与正确答案（猫）之间的差异很小。学习的目标是减少所有观察结果之间差异的总和。大多数学习模型可以看作是优化理论和统计估计的直接应用。[112][120]

　　 学习率

　　 学习率定义了模型在每次观察中调整错误时采取的修正步骤的大小。[121] 高学习率可以缩短训练时间，但会导致最终精度较低；而低学习率则需要更长时间，但可能带来更高的精度。优化方法如 Quickprop 主要旨在加速错误最小化，而其他改进则主要致力于提高可靠性。为了避免网络内的振荡（例如，连接权重交替变化），并改善收敛速度，改进的方法采用自适应学习率，根据需要调整学习率的增减。[122] 动量的概念使得梯度和之前变化之间的平衡得以加权，从而权重调整在某种程度上依赖于先前的变化。接近 0 的动量强调梯度，而接近 1 的动量则强调最后的变化。

　　 代价函数

　　 虽然可以随意定义代价函数，但通常选择是根据函数的理想属性（例如凸性）或因为它来自于模型本身（例如在概率模型中，模型的后验概率可以用作反向代价）来决定的。

　　 反向传播

　　 反向传播是一种方法，用于调整连接权重，以弥补在学习过程中发现的每个错误。错误量会在各个连接之间有效地分配。技术上，反向传播计算的是代价函数相对于给定状态的权重的梯度（导数）。权重更新可以通过随机梯度下降或其他方法来完成，例如极限学习机，[123] "no-prop" 网络，[124] 无回溯训练，[125] "无权重" 网络，[126][127] 和非连接主义神经网络。

4. 学习范式

　　 机器学习通常分为三种主要的学习范式：监督学习、无监督学习和强化学习。每种范式对应一种特定的学习任务。

　　 监督学习

　　 监督学习使用一组成对的输入和期望输出。学习任务是为每个输入产生期望的输出。在这种情况下，代价函数与消除错误推断有关。常用的代价函数是均方误差，它试图最小化网络输出与期望输出之间的平均平方误差。适合监督学习的任务包括模式识别（也称为分类）和回归（也称为函数逼近）。监督学习还适用于序列数据（例如，手写、语音和手势识别）。可以将其视为带有 “教师” 的学习形式，教师通过提供对目前得到的解决方案质量的持续反馈来指导学习。

　　 无监督学习

　　 在无监督学习中，输入数据与代价函数一起提供，代价函数是数据 \( x \) 和网络输出的某个函数。代价函数依赖于任务（模型领域）以及任何先验假设（模型的隐式属性、参数和观察变量）。举个简单的例子，考虑模型 \( f(x) = a \)，其中 \( a \) 是常数，代价为 \( C = E[(x - f(x))^2] \)。最小化这个代价函数会得到一个值 \( a \)，它等于数据的均值。代价函数可以更加复杂，其形式取决于应用。例如，在压缩中，代价函数可能与输入 \( x \) 和输出 \( f(x) \) 之间的互信息有关；而在统计建模中，它可能与给定数据的模型的后验概率有关（注意，在这两个例子中，这些量应当是最大化而非最小化）。无监督学习范式中的任务通常是估计问题；其应用包括聚类、统计分布估计、压缩和过滤。

　　 强化学习

　　 在一些应用中，如玩视频游戏，行动者（agent）执行一系列动作，每执行一个动作后，从环境中接收一个通常无法预测的反馈。目标是赢得游戏，即产生最积极（成本最低）的响应。在强化学习中，目标是通过加权网络（制定策略），执行能够最小化长期（预期累计）成本的动作。在每个时间点，代理执行一个动作，环境根据一些（通常是未知的）规则生成一个观察值和即时成本。规则和长期成本通常只能被估算。在任何时刻，代理需要决定是探索新的动作以发现其成本，还是利用之前的学习结果来更快地进行决策。

　　 形式上，环境被建模为一个马尔可夫决策过程（MDP），其中有状态 \( s_1, \dots, s_n \in S \) 和动作 \( a_1, \dots, a_m \in A \)。由于状态转移是未知的，因此使用概率分布来代替：即时成本分布 \( P(c_t | s_t) \)、观察分布 \( P(x_t | s_t) \) 和转移分布 \( P(s_{t+1} | s_t, a_t) \)，而策略被定义为给定观察结果下的条件动作分布。两者结合起来，定义了一个马尔可夫链（MC）。目标是发现成本最低的马尔可夫链。

　　 在这些应用中，人工神经网络（ANNs）作为学习组件。[132][133] 动态规划与 ANNs 结合（形成神经动态规划，Neurodynamic Programming）[134] 已被应用于解决如车辆调度[135]、视频游戏、自然资源管理[136][137]和医学[138]等问题，因为 ANNs 能够在减少离散化网格密度的情况下，仍然有效减轻准确性损失，这对于数值近似控制问题的解决尤为重要。强化学习范式下的任务通常是控制问题、游戏和其他顺序决策任务。

　　 自学习

　　 神经网络中的自学习概念在 1982 年被引入，同时提出了一种能够自学习的神经网络，称为交叉适应阵列（Crossbar Adaptive Array, CAA）。[139] 该系统仅有一个输入——情况 \( s \)，和一个输出——行为（或动作）\( a \)。它既没有来自外部的建议输入，也没有来自环境的外部强化输入。CAA 通过交叉方式计算关于动作的决策和对于遇到情况的情感（感受）。该系统由认知与情感之间的互动驱动。[140] 给定记忆矩阵 \( W = ||w(a, s)|| \)，每次迭代中的交叉自学习算法执行以下计算：

　　
在情况 \( s \) 下执行动作 \( a \)；
接受结果情况 \( s' \)；
计算在结果情况中的情感 \( v(s') \)；
更新交叉适应记忆：\( w'(a, s) = w(a, s) + v(s') \)。

　　 反向传播的值（次级强化）是对结果情况的情感。CAA 存在于两个环境中，一个是行为环境，系统在其中执行动作；另一个是遗传环境，CAA 在其中初次且唯一一次接收关于将要遇到的情况的初步情感。接收到来自遗传环境的基因组向量（物种向量）后，CAA 将在行为环境中学习目标寻求行为，这个环境包含了既有可取的情况也有不可取的情况。[141]

　　 神经进化 神经进化可以通过进化计算来创建神经网络的拓扑结构和权重。它与复杂的梯度下降方法具有竞争力。[142][143] 神经进化的一个优势是，它可能不容易陷入 “死胡同”。[144]

随机神经网络

　　 源自 Sherrington-Kirkpatrick 模型的随机神经网络是一种通过引入随机变化到网络中的人工神经网络，可以通过给网络的人工神经元提供随机传输函数[需要引用]，或通过赋予它们随机权重来实现。这使得它们成为优化问题的有用工具，因为随机波动帮助网络摆脱局部最小值。[145] 使用贝叶斯方法训练的随机神经网络被称为贝叶斯神经网络。[146]

其他

　　 在贝叶斯框架中，选择一个分布来对允许的模型集合进行建模，以最小化成本。进化方法[147]、基因表达编程[148]、模拟退火[149]、期望最大化、非参数方法和粒子群优化[150]是其他学习算法。收敛递归是一种用于小脑模型发音控制器（CMAC）神经网络的学习算法。[151][152]

　　 Modes

　　 有两种学习模式：随机学习和批量学习。在随机学习中，每个输入都会导致一次权重调整。在批量学习中，权重是基于一批输入进行调整的，错误会在批量中累积。随机学习通过使用从一个数据点计算出的局部梯度引入 “噪声”，这可以减少网络陷入局部最小值的概率。然而，批量学习通常会更快且更稳定地向局部最小值下降，因为每次更新都朝着批量的平均误差方向进行。一种常见的折衷方法是使用 “迷你批次”，即从整个数据集中随机选择的包含样本的小批次。

5. 类型

　　 人工神经网络（ANNs）已经发展成一个广泛的技术家族，推动了多个领域的技术进步。最简单的类型包括一个或多个静态组件，如单元数量、层数、单元权重和拓扑结构。动态类型允许通过学习使其中一个或多个组件发生变化。后者要复杂得多，但可以缩短学习周期并产生更好的结果。一些类型允许或要求学习由操作员 “监督”，而另一些则独立运作。有些类型完全在硬件上运行，而其他类型则纯软件实现，运行在通用计算机上。

　　 一些主要的突破包括：

6. 网络设计

　　 使用人工神经网络（ANNs）需要了解其特点。

　　 。

　　 神经架构搜索（NAS）：NAS 利用机器学习自动化 ANN 设计。各种 NAS 方法已经设计出与人工设计系统相媲美的网络。基本的搜索算法是提出一个候选模型，评估其在数据集上的表现，并利用结果作为反馈来指导 NAS 网络的学习。[164] 可用的系统包括 AutoML 和 AutoKeras。[165] scikit-learn 库提供了一些函数，帮助从零开始构建深度网络。然后可以使用 TensorFlow 或 Keras 来实现深度网络。

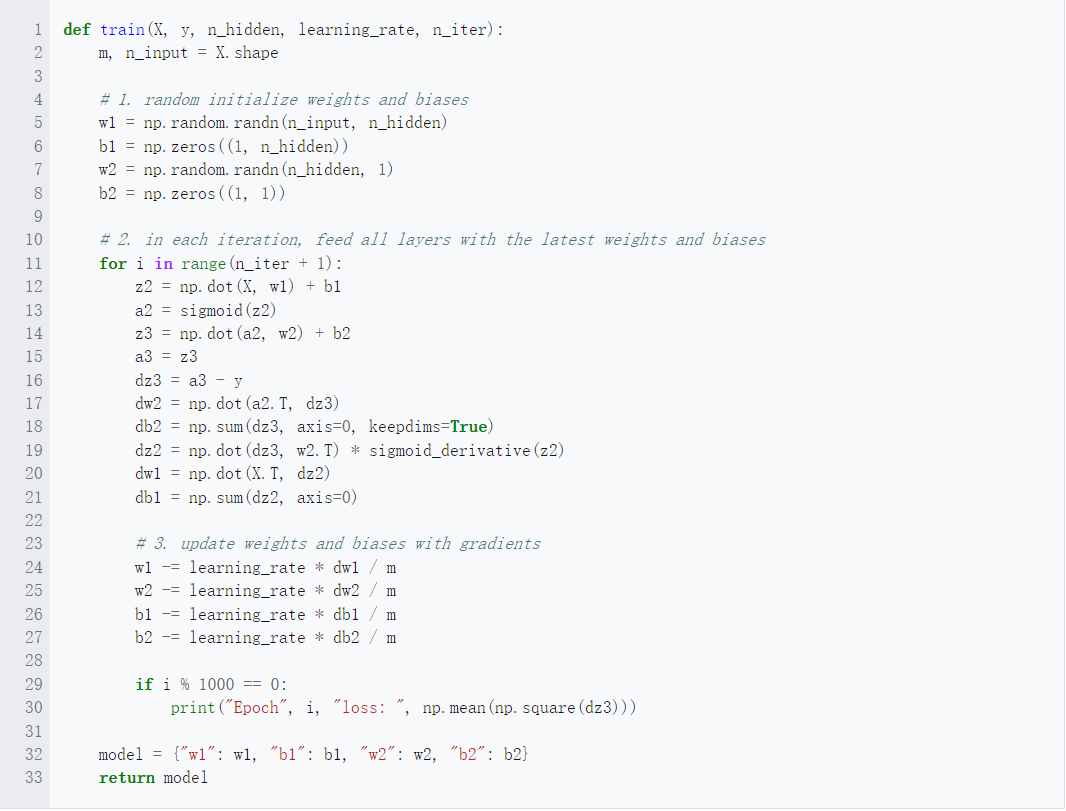
　　 超参数也需要在设计过程中定义（它们不是通过学习获得的），它们决定了每层有多少个神经元、学习率、步长、步伐、深度、感受野和填充（对于 CNN）等事项。[166]

　　 下面的 Python 代码片段概述了训练函数，它使用训练数据集、隐藏层单元的数量、学习率和迭代次数作为参数：

图
图 3

7. 应用

　　 由于人工神经网络能够重现和建模非线性过程，它们在许多学科中找到了应用。包括：

　　 人工神经网络（ANNs）已被用于诊断多种类型的癌症[184][185]，并通过仅使用细胞形状信息区分高度侵袭性的癌细胞系和低侵袭性的细胞系[186][187]。

　　 人工神经网络已被用于加速自然灾害对基础设施的可靠性分析[188][189]，并预测地基沉降[190]。它还可用于通过模拟降水-径流来缓解洪水[191]。ANNs 也已被用于在地球科学中构建黑箱模型，如水文学[192][193]、海洋建模和沿海工程[194][195]，以及地貌学[196]。ANNs 在网络安全中得到了应用，目标是区分合法活动和恶意活动。例如，机器学习已被用于分类 Android 恶意软件[197]，识别属于威胁行为者的域名，以及检测存在安全风险的 URL[198]。目前正在研究为渗透测试、检测僵尸网络[199]、信用卡欺诈[200]和网络入侵设计的 ANN 系统。

　　 人工神经网络已被提出作为解决物理学中偏微分方程的工具[201][202][203]，并模拟多体开放量子系统的性质[204][205][206][207]。在大脑研究中，ANNs 研究了单个神经元的短期行为[208]，神经回路的动态是由单个神经元之间的相互作用产生的，以及行为如何从表示完整子系统的抽象神经模块中产生。研究还考虑了神经系统的长期和短期可塑性以及它们与学习和记忆的关系，从单个神经元到系统层面。

　　 使用人工神经网络进行物体识别，可以从图片中创建用户兴趣的个人资料[209]。

　　 除了传统的应用领域，人工神经网络在跨学科研究中也越来越受到利用，例如材料科学。例如，图神经网络（GNNs）已经证明其在新稳定材料发现中的能力，通过高效预测晶体的总能量来扩展深度学习的应用。这一应用突显了 ANNs 在解决复杂问题方面的适应性和潜力，超越了预测建模和人工智能的领域，为科学发现和创新开辟了新路径[210]。

8. 理论属性

计算能力

　　 多层感知机（Multilayer Perceptron, MLP）是一个通用的函数逼近器，这一点已通过普遍逼近定理得到证明。然而，这一证明并没有对所需的神经元数量、网络拓扑、权重以及学习参数提供构造性的指导。

　　 具有有理数权重（而非全精度实数权重）的特定递归架构具有通用图灵机的能力[211]，只需有限数量的神经元和标准的线性连接。此外，使用无理数作为权重值会使得机器具有超图灵能力[212][213]（未验证）。

容量

　　 一个模型的 “容量” 属性对应于其对任何给定函数建模的能力。它与网络中可以存储的信息量以及复杂性的概念相关。社区已知有两种容量的概念：信息容量和 VC 维度（Vapnik-Chervonenkis Dimension）。感知机的信息容量在 Sir David MacKay 的书中得到了广泛讨论[214]，该书总结了 Thomas Cover 的工作[215]。标准神经元（非卷积神经元）网络的容量可以通过四条规则推导出来[216]，这些规则源于将神经元理解为电气元件的理论。信息容量捕捉了给定任何输入数据时，网络能够建模的函数。第二个概念是 VC 维度。VC 维度使用测度理论的原理，找出在最佳条件下的最大容量，即给定特定形式的输入数据。如在[214]中所述，任意输入的 VC 维度是感知机信息容量的一半。任意点的 VC 维度有时被称为 “记忆容量”[217]。

收敛性

　　 模型可能无法始终收敛到单一解，首先是因为存在局部最小值，这取决于代价函数和模型。其次，所使用的优化方法可能无法保证在距离任何局部最小值较远时就收敛。第三，对于足够大的数据或参数，一些方法变得不切实际。

　　 另一个值得提到的问题是，训练过程中可能会经过一些鞍点，从而导致收敛方向错误。

　　 某些类型的 ANN 架构的收敛行为比其他类型更为清楚。当网络的宽度趋近于无穷大时，ANN 在训练过程中可以通过其一阶泰勒展开式很好地描述，因此继承了仿射模型的收敛行为[218][219]。另一个例子是当参数较小时，观察到 ANN 通常从低频到高频拟合目标函数。这种行为被称为神经网络的频谱偏差或频率原理[220][221][222][223]。这一现象与一些著名的迭代数值方法（如雅可比法）行为相反。深层神经网络通常对低频函数有更强的偏好[224]。

泛化与统计学

　　 目标是创建一个能够很好地泛化到未见过的样本的系统的应用，面临着过度训练的可能性。这种问题出现在复杂或过度指定的系统中，当网络的容量远远超过所需的自由参数时，就会出现过度训练。解决过度训练的有两种方法。第一种方法是使用交叉验证和类似技术检查是否存在过度训练，并选择超参数以最小化泛化误差。

　　 第二种方法是使用某种形式的正则化。这个概念出现在概率（贝叶斯）框架中，在这种框架下，正则化可以通过选择对简单模型的更大先验概率来执行；它也出现在统计学习理论中，在该理论中，目标是最小化两个量：‘经验风险’和‘结构风险’，这大致对应于训练集上的误差以及由于过拟合导致在未见过的数据上的预测误差。

图
图 4：神经网络的置信度分析

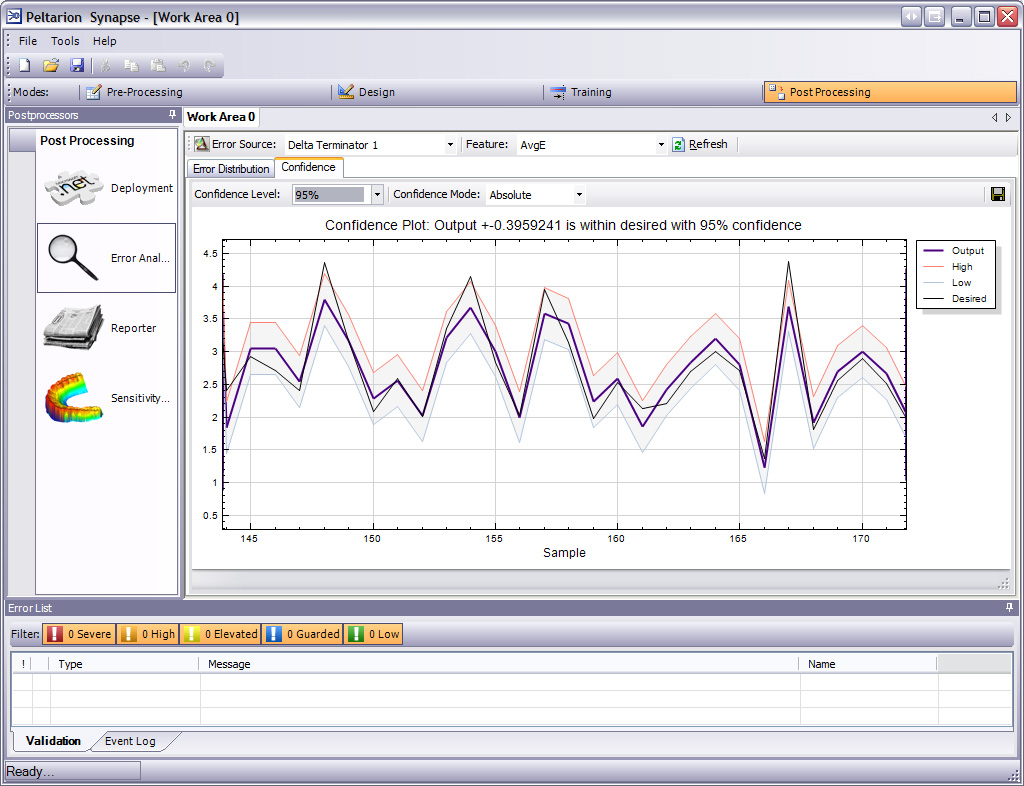
　　 使用均方误差（MSE）成本函数的监督神经网络可以使用正式的统计方法来确定训练模型的置信度。验证集上的 MSE 可以作为方差的估计值。然后，可以使用该值来计算网络输出的置信区间，假设输出符合正态分布。只要输出概率分布保持不变，并且网络没有被修改，这种置信度分析在统计学上是有效的。

　　 通过在神经网络的输出层（或在基于组件的网络中使用软最大化组件）上分配一个软最大化激活函数，这个函数是逻辑函数的广义形式，可以用于分类目标变量，输出值可以解释为后验概率。这在分类任务中非常有用，因为它提供了分类结果的确定性度量。

　　 软最大化激活函数为： \[ y_i = \frac{e^{x_i}}{\sum_{j=1}^{c} e^{x_j}}~ \]

9. 批评

训练

　　 神经网络，尤其是在机器人领域，常受到批评，因为它们需要大量的训练样本才能在现实世界中运行。任何学习机器都需要足够具代表性的示例，以便捕捉到能够使其泛化到新案例的潜在结构。潜在的解决方案包括：通过随机打乱训练示例，使用数值优化算法，在更改网络连接时不会采取过大的步骤，或者使用所谓的小批量训练，将示例分组，和/或为 CMAC 引入递归最小二乘算法。Dean Pomerleau 使用神经网络训练机器人车在多种道路类型上行驶（单车道、多车道、土路等），他的研究大部分致力于从单次训练经历中推断多个训练情景，并保持过去训练的多样性，以避免系统过度训练（例如，如果系统只被呈现连续的右转情景，它不应学会总是右转）。

理论

　　 人工神经网络（ANNs）的一个核心论点是，它们体现了处理信息的新型且强大的通用原则。然而，这些原则并没有明确的定义。通常有人声称[需要引用]，这些原则是从网络本身产生的。这使得简单的统计关联（人工神经网络的基本功能）能够被描述为学习或识别。1997 年，前《科学美国人》专栏作家亚历山大·杜德尼（Alexander Dewdney）评论道，人工神经网络具有 “只取不舍的特性，赋予其一种懒惰的气质，并且对这些计算系统的实际效果缺乏好奇心。没有人类的手（或头脑）干预；解决方案仿佛是魔法般自然而然地出现；似乎没有人学到什么。”[227] 对杜德尼的回应之一是，神经网络已成功地应用于许多复杂多样的任务，从自主飞行的飞机[228]到信用卡欺诈检测，再到精通围棋游戏。

　　 科技作家罗杰·布里奇曼评论道：

　　 “例如，神经网络之所以被批评，不仅因为它们被炒得天花乱坠（有什么不是？），还因为你可以在不了解其工作原理的情况下创建一个成功的网络：那些捕捉其行为的一堆数字很可能会是‘一个不透明、不可读的表格……作为科学资源毫无价值’。”

　　 尽管他强调科学与技术是不同的，杜德尼似乎在这里将神经网络批判为糟糕的科学，而实际上，大多数开发神经网络的人只是试图做出好的工程设计。即使是一个不可读的表格，如果有用的机器能够读取，仍然是非常值得拥有的。[229]

　　 虽然分析人工神经网络所学到的内容确实很困难，但比分析生物神经网络所学到的内容要容易得多。此外，近年来对人工智能可解释性的重视促成了基于注意力机制的可视化方法的发展，用于解释和理解已学到的神经网络。进一步的研究者正在逐渐揭示出一些通用的原则，这些原则使得学习机器能够成功。例如，Bengio 和 LeCun（2007）撰写了一篇关于局部学习与非局部学习、浅层架构与深层架构的文章。[230]

　　 生物大脑使用浅层和深层电路，如大脑解剖学所报告的那样，展现出各种各样的不变性。Weng[232]认为，大脑的自我连接主要是根据信号统计进行的，因此，序列级联无法捕捉所有主要的统计依赖关系。

硬件

　　 大型且高效的神经网络需要相当可观的计算资源。[233] 尽管大脑具有专门的硬件来处理通过神经元图进行信号处理，但即使在冯·诺依曼架构上模拟一个简化的神经元也可能消耗大量的内存和存储。此外，设计者通常需要通过许多连接及其相关的神经元传输信号，这需要巨大的 CPU 功率和时间。[需要引用]

　　 有人认为，神经网络在 21 世纪的复兴在很大程度上归功于硬件的进步：从 1991 年到 2015 年，计算能力，尤其是由 GPGPU（通用图形处理单元）提供的计算能力，已经增加了大约百万倍，使得标准的反向传播算法能够训练比以前深得多的多层网络。[38] 使用加速器，如 FPGA 和 GPU，可以将训练时间从几个月缩短到几天。[233][234]

　　 类脑工程（Neuromorphic engineering）或物理神经网络直接通过构建非冯·诺依曼芯片来解决硬件难题，从而在电路中直接实现神经网络。另一种为神经网络处理优化的芯片被称为张量处理单元（Tensor Processing Unit，TPU）。[235]

实际反例

　　 分析人工神经网络（ANN）所学到的内容比分析生物神经网络所学到的内容要容易得多。此外，致力于探索神经网络学习算法的研究人员正在逐渐揭示一些通用原则，这些原则使得学习机器能够成功。例如，局部学习与非局部学习以及浅层架构与深层架构的比较。[236]

混合方法

　　 混合模型（结合神经网络和符号方法）的支持者认为，这种混合能够更好地捕捉人类思维的机制。[237][238]

数据集偏差

　　 神经网络依赖于其训练数据的质量，因此低质量的数据或具有不平衡代表性的数据可能导致模型学习并延续社会偏见。[239][240] 当神经网络被应用于现实场景时，这些继承的偏见尤为关键，因为训练数据可能因某一特定种族、性别或其他属性的数据稀缺而不平衡。[239] 这种不平衡可能导致模型对代表性不足群体的理解和表现不充分，从而产生歧视性结果，进一步加剧社会不平等，尤其是在面部识别、招聘流程和执法等应用中。[240][241] 例如，2018 年，亚马逊不得不放弃一款招聘工具，因为该模型倾向于选择男性而非女性从事软件工程工作，这是因为该领域男性员工比例较高。[241] 该程序会惩罚任何带有 “woman” 一词或任何女性学院名称的简历。然而，使用合成数据可以帮助减少数据集偏差并增加数据集的代表性。[242]

10. 画廊

图
图 5

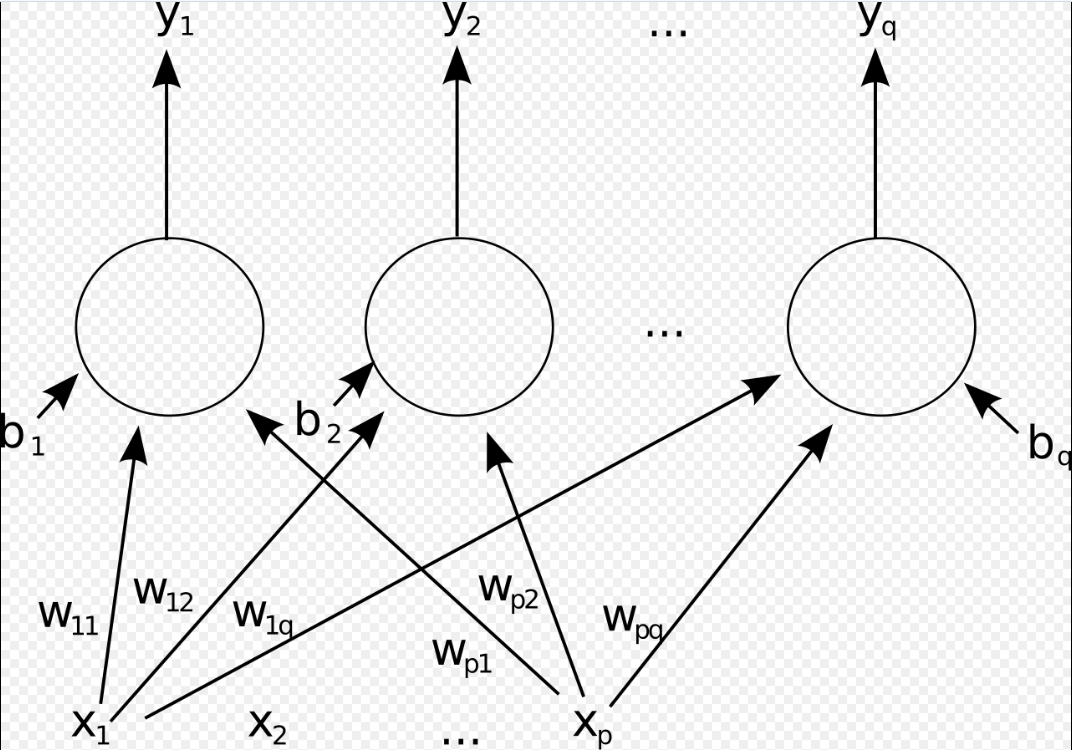
　　 一个单层前馈人工神经网络。为了清晰起见，箭头从 \( x_2 \) 出发的部分已省略。这个网络有 \( p \) 个输入和 \( q \) 个输出。在该系统中，第 \( q \) 个输出的值 \( y_q \) 计算公式为： \[ y_q = K \times \left( \sum_i (x_i \times w_{iq}) - b_q \right)~ \]

图
图 6：一个两层前馈人工神经网络
图
图 7：一个人工神经网络
图
图 8：一个人工神经网络依赖图
图
图 9：一个单层前馈人工神经网络，具有 4 个输入、6 个隐藏节点和 2 个输出。给定位置状态和方向，它输出基于轮子的控制值。
图
图 10：一个两层前馈人工神经网络，具有 8 个输入、2×8 个隐藏节点和 2 个输出。给定位置状态、方向和其他环境值，它输出基于推进器的控制值。
图
图 11：CMAC 神经网络的并行流水线结构。该学习算法可以在一步内收敛。

11. 最近的进展和未来方向

　　 人工神经网络（ANNs）已经取得了显著进展，特别是在建模复杂系统、处理大规模数据集以及适应各种应用领域的能力方面。过去几十年来，它们在图像处理、语音识别、自然语言处理、金融和医学等领域的广泛应用标志着其演变的一个重要阶段。

图像处理

　　 在图像处理领域，人工神经网络（ANNs）被广泛应用于图像分类、物体识别和图像分割等任务。例如，深度卷积神经网络（CNNs）在手写数字识别中发挥了重要作用，取得了最先进的表现。[243] 这展示了 ANNs 在有效处理和解读复杂视觉信息方面的能力，推动了从自动监控到医学影像等多个领域的进步。[243]

语音识别

　　 通过对语音信号的建模，ANNs 被用于诸如说话人识别和语音转文本转换等任务。深度神经网络架构在大词汇量连续语音识别中引入了显著的改进，超越了传统技术。[243][244] 这些进展使得更加精确和高效的语音激活系统得以开发，增强了技术产品中的用户界面。

自然语言处理

　　 在自然语言处理领域，人工神经网络（ANNs）被用于文本分类、情感分析和机器翻译等任务。它们使得开发出能够准确进行语言间翻译、理解文本数据中的上下文和情感、以及根据内容对文本进行分类的模型成为可能。[243][244] 这些进展对自动化客服、内容审核和语言理解技术具有重要意义。

控制系统

　　 在控制系统领域，ANNs 被用于建模动态系统，处理诸如系统识别、控制设计和优化等任务。例如，深度前馈神经网络在系统识别和控制应用中具有重要作用。

金融

　　 进一步信息：人工智能应用 § 交易与投资 ANNs（人工神经网络）被用于股市预测和信用评分：

　　 ANNs 需要高质量的数据和细致的调优，而其 “黑箱” 特性可能带来解释上的挑战。然而，持续的进展表明，ANNs 在金融领域仍然发挥着重要作用，提供有价值的洞察力，并增强风险管理策略。

医学

　　 ANNs 能够处理和分析庞大的医疗数据集。它们提高了诊断准确性，特别是在通过解读复杂的医学影像进行早期疾病检测以及预测患者的预后以进行个性化治疗计划方面。[244] 在药物发现中，ANNs 加速了潜在药物候选者的识别，并预测它们的疗效和安全性，从而显著减少了开发时间和成本。[243] 此外，它们在个性化医疗和医疗数据分析中的应用，促进了定制治疗和高效的患者护理管理。[244] 当前的研究旨在解决剩余的挑战，如数据隐私和模型可解释性问题，并扩展 ANNs 在医学中的应用范围。[citation needed]

　　 内容创作 ANNs，如生成对抗网络（GAN）和变压器（transformers），广泛应用于多个行业的内容创作。[245] 这是因为深度学习模型能够从大量数据集中学习艺术家或音乐家的风格，并创作出全新的艺术作品和音乐作品。例如，DALL-E 是一种深度神经网络，经过在互联网上 650 百万对图像和文本的训练，可以根据用户输入的文本创建艺术作品。[246] 在音乐领域，变压器被用于为广告和纪录片创作原创音乐，例如 AIVA 和 Jukedeck 等公司。[247] 在营销行业，生成模型被用于为消费者创建个性化广告。[245] 此外，主要电影公司正在与科技公司合作，分析电影的财务成功，例如 2020 年华纳兄弟与科技公司 Cinelytic 建立的合作伙伴关系。[248] 此外，神经网络还被用于视频游戏创作，在这些游戏中，非玩家角色（NPC）可以根据当前游戏中的所有角色作出决策。[249]

12. 参见

13. 参考文献

  1. Hardesty, L. (2017 年 4 月 14 日). "解释：神经网络". MIT 新闻办公室. 于 2024 年 3 月 18 日存档. 2022 年 6 月 2 日检索.
  2. Yang, Z., Yang, Z. (2014). 《综合生物医学物理学》. 卡罗林斯卡学院，瑞典斯德哥尔摩：Elsevier. 第 1 页. ISBN 978-0-444-53633-4. 于 2022 年 7 月 28 日存档. 2022 年 7 月 28 日检索.
  3. Bishop, C. M. (2006 年 8 月 17 日). 《模式识别与机器学习》. 纽约：Springer. ISBN 978-0-387-31073-2.
  4. Vapnik, V. N. (1998). 《统计学习理论的本质》 (修订版第 2 版). 纽约、柏林、海德堡：Springer. ISBN 978-0-387-94559-0.
  5. Ian Goodfellow, Yoshua Bengio, Aaron Courville (2016). 《深度学习》. MIT 出版社. 于 2016 年 4 月 16 日存档. 2016 年 6 月 1 日检索.
  6. Ferrie, C., Kaiser, S. (2019). 《神经网络给宝宝们》. Sourcebooks. ISBN 978-1-4926-7120-6.
  7. Mansfield Merriman, "最小二乘法相关文献列表"
  8. Stigler, S. M. (1981). "高斯与最小二乘法的发明". 《统计学年刊》. 9 (3): 465–474. doi:10.1214/aos/1176345451.
  9. Bretscher, O. (1995). 《线性代数与应用》 (第 3 版). 上萨德尔河，NJ：Prentice Hall.
  10. Schmidhuber, J. (2022). "现代人工智能与深度学习的注解历史". arXiv:2212.11279 [cs.NE].
  11. Stigler, S. M. (1986). 《统计学史：1900 年之前的不确定性度量》. 剑桥：哈佛大学. ISBN 0-674-40340-1.
  12. McCulloch, W. S., Pitts, W. (1943 年 12 月). "神经活动中固有思想的逻辑演算". 《数学生物物理学公报》. 5 (4): 115–133. doi:10.1007/BF02478259. ISSN 0007-4985.
  13. Kleene, S. (1956). "神经网络和有限自动机中的事件表示". 《数学研究年鉴》. 第 34 号. 普林斯顿大学出版社. 第 3–41 页. 2017 年 6 月 17 日检索.
  14. Hebb, D. (1949). 《行为的组织》. 纽约：Wiley. ISBN 978-1-135-63190-1.
  15. Farley, B., W. A. Clark (1954). "通过数字计算机模拟自组织系统". 《信息理论 IRE 交易》. 4 (4): 76–84. doi:10.1109/TIT.1954.1057468.
  16. Rochester N, J.H. Holland, L.H. Habit, W.L. Duda (1956). "使用大型数字计算机对大脑细胞组理论的作用进行测试". 《信息理论 IRE 交易》. 2 (3): 80–93. doi:10.1109/TIT.1956.1056810.
  17. Haykin (2008). 《神经网络与学习机器》，第 3 版.
  18. Rosenblatt, F. (1958). "感知器：大脑中信息存储与组织的概率模型". 《心理学评论》. 65 (6): 386–408. CiteSeerX 10.1.1.588.3775. doi:10.1037/h0042519. PMID 13602029. S2CID 12781225.
  19. Werbos, P. (1975). 《超越回归：行为科学预测与分析的新工具》。
  20. Rosenblatt, F. (1957). "感知器——一种感知和识别自动机". 报告 85-460-1. 康奈尔航空实验室.
  21. Olazaran, M. (1996). "感知器争议官方历史的社会学研究". 《社会科学研究》. 26 (3): 611–659. doi:10.1177/030631296026003005. JSTOR 285702. S2CID 16786738.
  22. Joseph, R.D. (1960). 《感知器理论贡献》，康奈尔航空实验室报告 No. VG-11 96--G-7, 布法罗。
  23. Russel, Stuart, Norvig, Peter (2010). 《人工智能：一种现代方法》 (PDF) (第 3 版). 美国：皮尔逊教育. 第 16-28 页. ISBN 978-0-13-604259-4.
  24. Rosenblatt F (1962). 《神经动力学原理》。斯巴达出版社，纽约。
  25. Ivakhnenko AG, Lapa VG (1967). 《控制论与预测技术》。美国 Elsevier 出版公司。ISBN 978-0-444-00020-0。
  26. Ivakhnenko A (1970 年 3 月). "工程控制论问题中的启发式自组织"。《自动化》。6 (2): 207–219. doi:10.1016/0005-1098(70)90092-0。
  27. Ivakhnenko A (1971). "复杂系统的多项式理论"（PDF）。《IEEE 系统、人类与控制论学报》。SMC-1 (4): 364–378. doi:10.1109/TSMC.1971.4308320. 已归档（PDF）于 2017 年 8 月 29 日。检索日期：2019 年 11 月 5 日。
  28. Robbins H, Monro S (1951). "随机逼近方法"。《数学统计年鉴》。22 (3): 400. doi:10.1214/aoms/1177729586。
  29. Amari S (1967). "自适应模式分类器理论"。《IEEE 学报》。EC (16): 279–307。
  30. Fukushima K (1969). "通过多层模拟阈值单元的网络提取视觉特征"。《IEEE 系统科学与控制论学报》。5 (4): 322–333. doi:10.1109/TSSC.1969.300225。
  31. Sonoda S, Murata N (2017). "具有无界激活函数的神经网络是通用近似器"。《应用与计算和声分析》。43 (2): 233–268. arXiv:1505.03654. doi:10.1016/j.acha.2015.12.005. S2CID 12149203。
  32. Ramachandran P, Barret Z, Quoc VL (2017 年 10 月 16 日). "寻找激活函数"。arXiv:1710.05941 [cs.NE]。
  33. Minsky M, Papert S (1969). 《感知器：计算几何学导论》。麻省理工学院出版社。ISBN 978-0-262-63022-1。
  34. Bozinovski S., Fulgosi A. (1976). "模式相似性与迁移学习对基础感知器训练的影响"（克罗地亚语原文）《信息学研讨会论文集》。3-121-5，布莱德。
  35. Bozinovski S. (2020). "回顾 1976 年关于神经网络迁移学习的第一篇论文"。《信息学》。44: 291–302。
  36. Fukushima K (1979). "一种不受位置偏移影响的模式识别机制的神经网络模型—Neocognitron"。《IECE 转录》。J62-A (10): 658–665. doi:10.1007/bf00344251. PMID 7370364. S2CID 206775608。
  37. Fukushima K (1980). "Neocognitron: 一种自组织神经网络模型，用于不受位置偏移影响的模式识别机制"。《生物控制论》。36 (4): 193–202. doi:10.1007/bf00344251. PMID 7370364. S2CID 206775608。
  38. Schmidhuber J (2015). "神经网络中的深度学习概述"。《神经网络》。61: 85–117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. PMID 25462637. S2CID 11715509.
  39. Leibniz GW (1920). 《莱布尼茨早期数学手稿：从卡尔·伊曼纽尔·格哈特出版的拉丁文文本翻译，并附有批判性和历史性注释》（莱布尼茨在 1676 年的论文中首次发布了链式法则）。开放法院出版社。ISBN 9780598818461。
  40. Kelley HJ (1960). "最优飞行路径的梯度理论"。《ARS 期刊》。30 (10): 947–954. doi:10.2514/8.5282。
  41. Linnainmaa S (1970). 《算法的累积舍入误差表示为局部舍入误差的泰勒展开》（硕士论文）（芬兰语）。赫尔辛基大学。第 6–7 页。
  42. Linnainmaa S (1976). "累积舍入误差的泰勒展开"。《BIT 数值数学》。16 (2): 146–160. doi:10.1007/bf01931367. S2CID 122357351。
  43. Ostrovski, G.M., Volin, Y.M., and Boris, W.W. (1971). "关于导数的计算"。《技术化学高等学校科学杂志》。13: 382–384。
  44. Schmidhuber J (2014 年 10 月 25 日). "谁发明了反向传播？"。《IDSIA》，瑞士。原文归档于 2024 年 7 月 30 日。检索日期：2024 年 9 月 14 日。
  45. Werbos P (1982). "非线性灵敏度分析进展的应用"（PDF）。《系统建模与优化》。斯普林格出版社。第 762–770 页。原文 PDF 归档于 2016 年 4 月 14 日。检索日期：2017 年 7 月 2 日。
  46. Anderson JA, Rosenfeld E, eds. (2000). 《Talking Nets: 神经网络的口述历史》。麻省理工学院出版社。doi:10.7551/mitpress/6626.003.0016. ISBN 978-0-262-26715-1。
  47. Werbos PJ (1994). 《反向传播的根源：从有序导数到神经网络与政治预测》。纽约：约翰·威立出版社。ISBN 0-471-59897-6。
  48. Rumelhart DE, Hinton GE, Williams RJ (1986 年 10 月). "通过反向传播误差学习表征"。《自然》。323 (6088): 533–536. Bibcode:1986Natur.323..533R. doi:10.1038/323533a0. ISSN 1476-4687。
  49. Fukushima K, Miyake S (1982 年 1 月 1 日). "Neocognitron: 一种新型的容忍变形和位置偏移的模式识别算法"。《模式识别》。15 (6): 455–469. Bibcode:1982PatRe..15..455F. doi:10.1016/0031-3203(82)90024-3. ISSN 0031-3203。
  50. Waibel A (1987 年 12 月). "使用时延神经网络进行音素识别"（PDF）。《电子信息与通信工程学会会议》。东京，日本。
  51. Alexander Waibel 等人, "使用时延神经网络进行音素识别"，《IEEE 声学、语音与信号处理汇刊》，第 37 卷，第 3 期，第 328–339 页，1989 年 3 月。
  52. Zhang W (1988). "位移不变模式识别神经网络及其光学架构"。《日本应用物理学会年会论文集》。
  53. LeCun 等人, "反向传播应用于手写邮政编码识别"，《神经计算》，第 1 期，第 541–551 页，1989 年。
  54. Zhang W (1990). "具有局部空间不变互联的并行分布处理模型及其光学架构"。《应用光学》。29 (32): 4790–7. Bibcode:1990ApOpt..29.4790Z. doi:10.1364/AO.29.004790. PMID 20577468。
  55. Zhang W (1991). "基于学习网络的人眼角膜内皮图像处理"。《应用光学》。30 (29): 4211–7. Bibcode:1991ApOpt..30.4211Z. doi:10.1364/AO.30.004211. PMID 20706526。
  56. Zhang W (1994). "使用位移不变人工神经网络在数字乳腺 X 光图像中计算聚集微钙化"。《医学物理》。21 (4): 517–24. Bibcode:1994MedPh..21..517Z. doi:10.1118/1.597177. PMID 8058017。
  57. LeCun Y, Léon Bottou, Yoshua Bengio, Patrick Haffner (1998). "基于梯度学习的文档识别"（PDF）。《IEEE 会议论文集》。86 (11): 2278–2324. CiteSeerX 10.1.1.32.9552. doi:10.1109/5.726791. S2CID 14542261. 检索日期：2016 年 10 月 7 日。
  58. Qian, Ning, 和 Terrence J. Sejnowski. "使用神经网络模型预测球状蛋白的二级结构。"《分子生物学杂志》, 第 202 卷，第 4 期（1988 年）：865–884。
  59. Bohr, Henrik, Jakob Bohr, Søren Brunak, Rodney MJ Cotterill, Benny Lautrup, Leif Nørskov, Ole H. Olsen, 和 Steffen B. Petersen. "通过神经网络预测蛋白质二级结构及同源性：视紫红质中的α-螺旋"。《FEBS 快报》, 第 241 期（1988 年）：223–228。
  60. Rost, Burkhard, 和 Chris Sander. "以超过 70%的准确度预测蛋白质二级结构。"《分子生物学杂志》, 第 232 卷，第 2 期（1993 年）：584–599。
  61. Amari SI (1972 年 11 月). "通过自组织网络学习模式和模式序列"。《IEEE 计算机汇刊》。C-21 (11): 1197–1206. doi:10.1109/T-C.1972.223477. ISSN 0018-9340。
  62. Hopfield JJ (1982). "神经网络与具有突现集体计算能力的物理系统"。《美国科学院院刊》。79 (8): 2554–2558. Bibcode:1982PNAS...79.2554H. doi:10.1073/pnas.79.8.2554. PMC 346238. PMID 6953413。
  63. Espinosa-Sanchez JM, Gomez-Marin A, de Castro F (2023 年 7 月 5 日). "Cajal 和 Lorente de Nó 神经科学对控制论诞生的重要性"。《神经科学家》。doi:10.1177/10738584231179932. hdl:10261/348372. ISSN 1073-8584. PMID 37403768。
  64. “reverberating circuit”。《牛津参考书》。检索日期：2024 年 7 月 27 日。
  65. Bozinovski, S. (1982). "使用二次强化的自学习系统"。在 Trappl, Robert (编)，《控制论与系统研究：第六届欧洲控制论与系统研究会议论文集》。North-Holland 出版社，第 397–402 页。ISBN 978-0-444-86488-8。
  66. Bozinovski S. (1995) "神经遗传体与自我强化学习系统的结构理论"。CMPSCI 技术报告 95-107，马萨诸塞大学阿默斯特分校。
  67. R. Zajonc (1980) "感觉与思维：偏好无需推理"。《美国心理学家》，35 (2)：151-175。
  68. Lazarus R. (1982) "情感与认知关系的思考"，《美国心理学家》，37 (9)：1019-1024。
  69. Bozinovski, S. (2014) "自 1981 年以来在人工神经网络中建模认知-情感交互机制"，《计算机科学学报》，第 255–263 页 (https://core.ac.uk/download/pdf/81973924.pdf)。
  70. Schmidhuber J (1991 年 4 月). "神经序列分块器"（PDF）。TR FKI-148，慕尼黑工业大学。
  71. Schmidhuber J (1992). "使用历史压缩原理学习复杂的扩展序列（基于 TR FKI-148，1991）"（PDF）。《神经计算》。4 (2)：234–242。doi:10.1162/neco.1992.4.2.234。S2CID 18271205。
  72. Schmidhuber J (1993). Habilitation 论文：系统建模与优化（PDF）。第 150 页及以后展示了在展开的 RNN 中跨越 1200 层的信用分配。
  73. S. Hochreiter. "动态神经网络的研究"，2015 年 3 月 6 日存档于 Wayback Machine，学位论文。慕尼黑工业大学计算机科学系。导师：J. Schmidhuber，1991 年。
  74. Hochreiter S 等人 (2001 年 1 月 15 日)。"循环网络中的梯度流：学习长期依赖性的困难"。在 Kolen JF, Kremer SC (编辑)。《动态递归网络的现场指南》。约翰·威利父子公司。ISBN 978-0-7803-5369-5。2017 年 6 月 26 日检索。
  75. Sepp Hochreiter, Jürgen Schmidhuber (1995 年 8 月 21 日)，《长短期记忆》，Wikidata Q98967430。
  76. Hochreiter S, Schmidhuber J (1997 年 11 月 1 日)。“长短期记忆”。《神经计算》。9 (8)：1735–1780。doi:10.1162/neco.1997.9.8.1735。PMID 9377276。S2CID 1915014。
  77. Gers F, Schmidhuber J, Cummins F (1999)。"学习遗忘：使用 LSTM 进行持续预测"。第 9 届国际人工神经网络会议：ICANN '99。第 1999 卷，第 850–855 页。doi:10.1049/cp:19991218。ISBN 0-85296-721-7。
  78. Ackley DH, Hinton GE, Sejnowski TJ (1985 年 1 月 1 日)。“玻尔兹曼机的学习算法”《认知科学》。9 (1)：147–169。doi:10.1016/S0364-0213(85)80012-4。ISSN 0364-0213。
  79. Smolensky P (1986)。“第 6 章：动态系统中的信息处理：和谐理论的基础” (PDF)。在 Rumelhart DE, McLelland JL (编辑)，《并行分布处理：认知微观结构的探索，第 1 卷：基础》。麻省理工学院出版社，第 194–281 页。ISBN 0-262-68053-X。
  80. Peter D, Hinton GE, Neal RM, Zemel RS (1995)。“赫尔姆霍兹机”。《神经计算》。7 (5)：889–904。doi:10.1162/neco.1995.7.5.889。hdl:21.11116/0000-0002-D6D3-E。PMID 7584891。S2CID 1890561。
  81. Hinton GE, Dayan P, Frey BJ, Neal R (1995 年 5 月 26 日)。“无监督神经网络的 wake-sleep 算法”。《科学》。268 (5214)：1158–1161。Bibcode:1995Sci...268.1158H。doi:10.1126/science.7761831。PMID 7761831。S2CID 871473。
  82. 2012 年 Kurzweil AI 采访，2018 年 8 月 31 日存档于 Wayback Machine，采访了 Juergen Schmidhuber，讨论了他的深度学习团队在 2009-2012 年间赢得的八个竞赛。
  83. "How bio-inspired deep learning keeps winning competitions | KurzweilAI"。kurzweilai.net。2018 年 8 月 31 日存档。2017 年 6 月 16 日检索。
  84. Cireşan DC, Meier U, Gambardella LM, Schmidhuber J (2010 年 9 月 21 日)。“深度、大型、简单的神经网络用于手写数字识别”。《神经计算》。22 (12)：3207–3220。arXiv:1003.0358。doi:10.1162/neco_a_00052。ISSN 0899-7667。PMID 20858131。S2CID 1918673。
  85. Ciresan DC, Meier U, Masci J, Gambardella L, Schmidhuber J (2011)。"灵活的高性能卷积神经网络用于图像分类"（PDF）。国际人工智能联合会议。doi:10.5591/978-1-57735-516-8/ijcai11-210。2014 年 9 月 29 日存档（PDF）。2017 年 6 月 13 日检索。
  86. Ciresan D, Giusti A, Gambardella LM, Schmidhuber J (2012)。Pereira F, Burges CJ, Bottou L, Weinberger KQ（编）。《神经信息处理系统进展 25》（PDF）。Curran Associates, Inc.第 2843–2851 页。2017 年 8 月 9 日存档（PDF）。2017 年 6 月 13 日检索。
  87. Ciresan D, Giusti A, Gambardella L, Schmidhuber J (2013)。"利用深度神经网络在乳腺癌组织学图像中检测有丝分裂"。医学图像计算与计算机辅助干预–MICCAI 2013。Lecture Notes in Computer Science。第 7908 卷，第 411–418 页。doi:10.1007/978-3-642-40763-5_51。ISBN 978-3-642-38708-1。PMID 24579167。
  88. Ciresan D, Meier U, Schmidhuber J (2012)。"用于图像分类的多列深度神经网络"。2012 IEEE 计算机视觉与模式识别会议。第 3642–3649 页。arXiv:1202.2745。doi:10.1109/cvpr.2012.6248110。ISBN 978-1-4673-1228-8。S2CID 2161592。
  89. Krizhevsky A, Sutskever I, Hinton G (2012)。"使用深度卷积神经网络进行 ImageNet 分类"（PDF）。NIPS 2012：神经信息处理系统，内华达州塔霍湖。2017 年 1 月 10 日存档（PDF）。2017 年 5 月 24 日检索。
  90. Simonyan K, Andrew Z (2014)。"用于大规模图像识别的非常深的卷积网络"。arXiv:1409.1556 [cs.CV]。
  91. Szegedy C (2015). "Going deeper with convolutions" (PDF). Cvpr2015. arXiv:1409.4842.
  92. Ng A, Dean J (2012). "Building High-level Features Using Large Scale Unsupervised Learning". arXiv:1112.6209 [cs.LG].
  93. Billings SA (2013). 非线性系统辨识：时间、频率和时空域中的 NARMAX 方法。Wiley。ISBN 978-1-119-94359-4。
  94. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, 等 (2014). 生成对抗网络（PDF）。《神经信息处理系统国际会议论文集》（NIPS 2014）。第 2672–2680 页。2019 年 11 月 22 日存档（PDF）。2019 年 8 月 20 日检索。
  95. Schmidhuber J (1991). "在模型构建神经控制器中实现好奇心和厌倦感的可能性"。《SAB'1991 会议论文集》。MIT Press/Bradford Books。第 222–227 页。
  96. Schmidhuber J (2020). "生成对抗网络是人工好奇心（1990）的特例，并且与可预测性最小化（1991）紧密相关"。《神经网络》。127：58–66。arXiv:1906.04493。doi:10.1016/j.neunet.2020.04.008。PMID 32334341。S2CID 216056336。
  97. "GAN 2.0: NVIDIA 的超现实人脸生成器"。SyncedReview.com。2018 年 12 月 14 日。2019 年 10 月 3 日检索。
  98. Karras T, Aila T, Laine S, Lehtinen J (2018 年 2 月 26 日)。"GAN 的渐进式增长：改善质量、稳定性和变化"。arXiv:1710.10196 [cs.NE]。
  99. "准备好，不要惊慌：合成媒体与深度伪造"。witness.org。2020 年 12 月 2 日存档。2020 年 11 月 25 日检索。
  100. Sohl-Dickstein J, Weiss E, Maheswaranathan N, Ganguli S (2015 年 6 月 1 日)。"使用非平衡热力学进行深度无监督学习"（PDF）。第 32 届国际机器学习会议论文集。37。PMLR：2256–2265。arXiv:1503.03585。
  101. Simonyan K, Zisserman A (2015 年 4 月 10 日)。"用于大规模图像识别的非常深的卷积网络"。arXiv:1409.1556。
  102. He K, Zhang X, Ren S, Sun J (2016). "深入探讨整流器：在 ImageNet 分类中超越人类级表现"。arXiv:1502.01852 [cs.CV]。
  103. He K, Zhang X, Ren S, Sun J (2015 年 12 月 10 日)。"深度残差学习用于图像识别"。arXiv:1512.03385。
  104. Srivastava RK, Greff K, Schmidhuber J (2015 年 5 月 2 日)。“高速公路网络”。arXiv:1505.00387 [cs.LG]。
  105. He K, Zhang X, Ren S, Sun J (2016). "深度残差学习用于图像识别"。2016 IEEE 计算机视觉与模式识别会议（CVPR）。拉斯维加斯，NV，美国：IEEE。第 770–778 页。arXiv:1512.03385。doi:10.1109/CVPR.2016.90。ISBN 978-1-4673-8851-1。
  106. Linn A (2015 年 12 月 10 日)。“微软研究人员赢得 ImageNet 计算机视觉挑战”。《AI 博客》。2024 年 6 月 29 日检索。
  107. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, 等 (2017 年 6 月 12 日)。“注意力是你所需要的一切”。arXiv:1706.03762 [cs.CL]。
  108. Schmidhuber J (1992)。"学习控制快速权重记忆：递归网络的替代方案"（PDF）。《神经计算》。4 (1)：131–139。doi:10.1162/neco.1992.4.1.131。S2CID 16683347。
  109. Katharopoulos A, Vyas A, Pappas N, Fleuret F (2020)。"变压器是 RNN：具有线性注意力的快速自回归变压器"。ICML 2020。PMLR。第 5156–5165 页。
  110. Schlag I, Irie K, Schmidhuber J (2021)。"线性变压器实际上是快速权重编程器"。ICML 2021。Springer。第 9355–9366 页。
  111. Wolf T, Debut L, Sanh V, Chaumond J, Delangue C, Moi A, 等 (2020)。"变压器：最先进的自然语言处理"。《2020 年自然语言处理经验方法会议：系统演示论文集》。第 38–45 页。doi:10.18653/v1/2020.emnlp-demos.6。S2CID 208117506。
  112. Zell A (2003)。"第 5.2 章"。《神经网络仿真》（德文版）（第 1 版）。Addison-Wesley。ISBN 978-3-89319-554-1。OCLC 249017987。
  113. 《人工智能》（第 3 版）。Addison-Wesley 出版公司。1992 年。ISBN 0-201-53377-4。
  114. Abbod MF (2007)。"人工智能在泌尿系统癌症管理中的应用"。《泌尿学杂志》。178 (4)：1150–1156。doi:10.1016/j.juro.2007.05.122。PMID 17698099。
  115. Dawson CW (1998)。"人工神经网络方法用于降水-径流建模"。《水文科学杂志》。43 (1)：47–66。Bibcode:1998HydSJ..43...47D。doi:10.1080/02626669809492102。
  116. 《机器学习词典》cse.unsw.edu.au。2018 年 8 月 26 日存档。2009 年 11 月 4 日检索。
  117. Ciresan D, Ueli Meier, Jonathan Masci, Luca M. Gambardella, Jurgen Schmidhuber (2011)。"灵活的高性能卷积神经网络用于图像分类"（PDF）。《第 22 届国际人工智能联合会议论文集—第二卷》。2：1237–1242。2022 年 4 月 5 日存档（PDF）。2022 年 7 月 7 日检索。
  118. Zell A (1994)。《神经网络仿真》（德文版）（第 1 版）。Addison-Wesley。第 73 页。ISBN 3-89319-554-8。
  119. Miljanovic M (2012 年 2 月至 3 月)。"递归神经网络与有限脉冲响应神经网络在时间序列预测中的比较分析"（PDF）。《印度计算机与工程杂志》。3 (1)。2024 年 5 月 19 日存档（PDF）。2019 年 8 月 21 日检索。
  120. Kelleher JD, Mac Namee B, D'Arcy A (2020)。"7-8"。《预测数据分析的机器学习基础：算法、实例与案例研究》（第 2 版）。剑桥，马萨诸塞：MIT 出版社。ISBN 978-0-262-36110-1。OCLC 1162184998。
  121. Wei J (2019 年 4 月 26 日)。"忘记学习率，衰减损失"。arXiv:1905.00094 [cs.LG]。
  122. Li Y, Fu Y, Li H, Zhang SW (2009 年 6 月 1 日)。"具有自适应学习率的反向传播神经网络改进训练算法"。2009 年国际计算智能与自然计算大会。第 1 卷。第 73–76 页。doi:10.1109/CINC.2009.111。ISBN 978-0-7695-3645-3。S2CID 10557754。
  123. Huang GB, Zhu QY, Siew CK (2006)。"极限学习机：理论与应用"。《神经计算》。70 (1)：489–501。CiteSeerX 10.1.1.217.3692。doi:10.1016/j.neucom.2005.12.126。S2CID 116858。
  124. Widrow B, 等（2013）。"无传播算法：一种新的多层神经网络学习算法"。《神经网络》。37：182–188。doi:10.1016/j.neunet.2012.09.020。PMID 23140797。
  125. Ollivier Y, Charpiat G (2015)。"无需回溯训练递归网络"。arXiv:1507.07680 [cs.NE]。
  126. Hinton GE (2010)。"限制玻尔兹曼机训练实用指南"。技术报告 UTML TR 2010-003。2021 年 5 月 9 日存档。2017 年 6 月 27 日检索。
  127. ESANN。2009 年。[完整引用待定]
  128. Bernard E (2021)。《机器学习导论》。香槟：Wolfram Media。第 9 页。ISBN 978-1-57955-048-6。2024 年 5 月 19 日存档。2023 年 3 月 22 日检索。
  129. Bernard E (2021)。《机器学习导论》。香槟：Wolfram Media。第 12 页。ISBN 978-1-57955-048-6。2024 年 5 月 19 日存档。2023 年 3 月 22 日检索。
  130. Bernard E (2021)。《机器学习导论》。Wolfram Media Inc. 第 9 页。ISBN 978-1-57955-048-6。2024 年 5 月 19 日存档。2022 年 7 月 28 日检索。
  131. Ojha VK, Abraham A, Snášel V (2017 年 4 月 1 日)。"前馈神经网络的元启发式设计：二十年研究回顾"。《人工智能工程应用》。60：97–116。arXiv:1705.05584。Bibcode:2017arXiv170505584O。doi:10.1016/j.engappai.2017.01.013。S2CID 27910748。
  132. Dominic, S., Das, R., Whitley, D., Anderson, C. (1991 年 7 月)。“神经网络的遗传强化学习”。IJCNN-91-西雅图国际神经网络联合会议。IJCNN-91-西雅图国际神经网络联合会议。美国华盛顿州西雅图：IEEE。第 71–76 页。doi:10.1109/IJCNN.1991.155315。ISBN 0-7803-0164-1。
  133. Hoskins J, Himmelblau, D.M. (1992)。"通过人工神经网络和强化学习进行过程控制"。《计算机与化学工程》。16 (4)：241–251。doi:10.1016/0098-1354(92)80045-B。
  134. Bertsekas D, Tsitsiklis J (1996)。《神经动态规划》。Athena 科学出版社。第 512 页。ISBN 978-1-886529-10-6。2021 年 6 月 29 日存档。2017 年 6 月 17 日检索。
  135. Secomandi N (2000)。"比较神经动态规划算法在具有随机需求的车辆调度问题中的应用"。《计算机与运筹学研究》。27 (11–12)：1201–1225。CiteSeerX 10.1.1.392.4034。doi:10.1016/S0305-0548(99)00146-X。
  136. de Rigo, D., Rizzoli, A. E., Soncini-Sessa, R., Weber, E., Zenesi, P. (2001)。"用于有效管理水库网络的神经动态规划"。《MODSIM 2001 会议论文集：国际建模与仿真大会》。MODSIM 2001，国际建模与仿真大会。澳大利亚堪培拉：澳大利亚与新西兰建模与仿真学会。doi:10.5281/zenodo.7481。ISBN 0-86740-525-2。2013 年 8 月 7 日存档。2013 年 7 月 29 日检索。
  137. Damas, M., Salmeron, M., Diaz, A., Ortega, J., Prieto, A., Olivares, G. (2000)。"遗传算法与神经动态规划：应用于供水网络"。《2000 年进化计算大会论文集》。2000 年进化计算大会。第 1 卷。美国加利福尼亚州 La Jolla：IEEE。第 7–14 页。doi:10.1109/CEC.2000.870269。ISBN 0-7803-6375-2。
  138. Deng G, Ferris, M.C. (2008)。"用于分段放射治疗规划的神经动态规划"。《医学优化》。斯普林格优化及其应用。第 12 卷。第 47–70 页。CiteSeerX 10.1.1.137.8288。doi:10.1007/978-0-387-73299-2_3。ISBN 978-0-387-73298-5。
  139. Bozinovski, S. (1982)。"使用次级强化学习的自学习系统"。在 R. Trappl（编）《控制论与系统研究：第六届欧洲控制论与系统研究会议论文集》中。北荷兰出版社。第 397–402 页。ISBN 978-0-444-86488-8。
  140. Bozinovski, S. (2014)。“自 1981 年以来在人工神经网络中建模认知与情感交互机制，存档于 2019 年 3 月 23 日。”《计算机科学学报》255-263 页。
  141. Bozinovski S, Bozinovska L (2001)。"自学习代理：基于交叉条值判断的情感联结主义理论"。《控制论与系统》。32 (6)：637–667。doi:10.1080/01969720118145。S2CID 8944741。
  142. Salimans T, Ho J, Chen X, Sidor S, Sutskever I (2017 年 9 月 7 日)。"进化策略作为强化学习的可扩展替代方案"。arXiv:1703.03864 [stat.ML]。
  143. Such FP, Madhavan V, Conti E, Lehman J, Stanley KO, Clune J (2018 年 4 月 20 日)。"深度神经进化：遗传算法是训练深度神经网络进行强化学习的有竞争力替代方案"。arXiv:1712.06567 [cs.NE]。
  144. "人工智能可以‘进化’解决问题"。《科学 | AAAS》。2018 年 1 月 10 日。2021 年 12 月 9 日存档。2018 年 2 月 7 日检索。
  145. Turchetti C (2004)。《神经网络的随机模型》，《人工智能前沿与应用：基于知识的智能工程系统》，第 102 卷，IOS 出版社，ISBN 978-1-58603-388-0。
  146. Jospin LV, Laga H, Boussaid F, Buntine W, Bennamoun M (2022)。"实践指南：贝叶斯神经网络教程——深度学习用户的学习手册"。《IEEE 计算智能杂志》。第 17 卷，第 2 期。第 29–48 页。arXiv:2007.06823。doi:10.1109/mci.2022.3155327。ISSN 1556-603X。S2CID 220514248。
  147. de Rigo, D., Castelletti, A., Rizzoli, A. E., Soncini-Sessa, R., Weber, E. (2005 年 1 月)。"一种选择性改进技术，用于加快水资源网络管理中的神经动态规划"。在 Pavel Zítek（编）《第 16 届 IFAC 世界大会论文集 – IFAC-PapersOnLine》中的论文。第 16 届 IFAC 世界大会。第 16 卷。捷克布拉格：IFAC。第 7–12 页。doi:10.3182/20050703-6-CZ-1902.02172。hdl:11311/255236。ISBN 978-3-902661-75-3。2012 年 4 月 26 日存档。2011 年 12 月 30 日检索。
  148. Ferreira C (2006)。"使用基因表达编程设计神经网络"。在 A. Abraham, B. de Baets, M. Köppen, B. Nickolay（编）《应用软计算技术：复杂性的挑战》（PDF）中。Springer-Verlag 出版社，第 517–536 页。2013 年 12 月 19 日存档。2012 年 10 月 8 日检索。
  149. Da, Y., Xiurun, G. (2005 年 7 月)。"基于粒子群优化技术与模拟退火的改进 PSO-ANN"。在 T. Villmann（编）《神经计算的新视角：第 11 届欧洲人工神经网络研讨会》中。第 63 卷。Elsevier 出版社，第 527–533 页。doi:10.1016/j.neucom.2004.07.002。2012 年 4 月 25 日存档。2011 年 12 月 30 日检索。
  150. Wu, J., Chen, E. (2009 年 5 月)。"基于粒子群优化技术与人工神经网络的降水预测的新型非参数回归集成方法"。在 Wang, H., Shen, Y., Huang, T., Zeng, Z.（编）《第 6 届国际神经网络研讨会 ISNN 2009》中的论文。Lecture Notes in Computer Science。第 5553 卷。Springer 出版社，第 49–58 页。doi:10.1007/978-3-642-01513-7_6。ISBN 978-3-642-01215-0。2014 年 12 月 31 日存档。2012 年 1 月 1 日检索。
  151. Ting Qin, Zonghai Chen, Haitao Zhang, Sifu Li, Wei Xiang, Ming Li (2004)。"基于 RLS 的 CMAC 学习算法"（PDF）。《神经处理通讯》。19 (1)：49–61。doi:10.1023/B:NEPL.0000016847.18175.60。S2CID 6233899。2021 年 4 月 14 日存档（PDF）。2019 年 1 月 30 日检索。
  152. Ting Qin, Haitao Zhang, Zonghai Chen, Wei Xiang (2005)。"连续 CMAC-QRLS 及其系统阵列"（PDF）。《神经处理通讯》。22 (1)：1–16。doi:10.1007/s11063-004-2694-0。S2CID 16095286。2018 年 11 月 18 日存档（PDF）。2019 年 1 月 30 日检索。
  153. LeCun Y, Boser B, Denker JS, Henderson D, Howard RE, Hubbard W, et al. (1989)。"反向传播应用于手写邮政编码识别"。《神经计算》。1 (4)：541–551。doi:10.1162/neco.1989.1.4.541。S2CID 41312633。
  154. Yann LeCun (2016)。"深度学习在线幻灯片"，2016 年 4 月 23 日存档于 Wayback Machine。
  155. Hochreiter S, Schmidhuber J (1997 年 11 月 1 日)。"长短时记忆"。《神经计算》。9 (8)：1735–1780。doi:10.1162/neco.1997.9.8.1735。ISSN 0899-7667。PMID 9377276。S2CID 1915014。
  156. Sak H, Senior A, Beaufays F (2014)。"用于大规模声学建模的长短时记忆递归神经网络架构"（PDF）。2018 年 4 月 24 日存档。
  157. Li X, Wu X (2014 年 10 月 15 日)。"构建基于长短时记忆的深度递归神经网络用于大词汇量语音识别"。arXiv:1410.4281 [cs.CL]。
  158. Fan Y, Qian Y, Xie F, Soong FK (2014)。"基于双向 LSTM 的递归神经网络的 TTS 合成"。《国际语音通信协会年会论文集，Interspeech》：1964–1968。2017 年 6 月 13 日检索。
  159. Schmidhuber J (2015)。"深度学习"。《学者百科全书》。10 (11)：85–117。Bibcode:2015SchpJ..1032832S。doi:10.4249/scholarpedia.32832。
  160. Zen H, Sak H (2015)。"单向长短时记忆递归神经网络与递归输出层用于低延迟语音合成"（PDF）。Google.com。ICASSP。第 4470–4474 页。2021 年 5 月 9 日存档（PDF）。2017 年 6 月 27 日检索。
  161. Bozinovski S, Bozinovska L (2001)。"自学习代理：基于交叉条值判断的情感联结主义理论"。《控制论与系统》。32 (6)：637–667。doi:10.1080/01969720118145。S2CID 8944741。
  162. Salimans T, Ho J, Chen X, Sidor S, Sutskever I (2017 年 9 月 7 日)。"进化策略作为强化学习的可扩展替代方案"。arXiv:1703.03864 [stat.ML]。
  163. Such FP, Madhavan V, Conti E, Lehman J, Stanley KO, Clune J (2018 年 4 月 20 日)。"深度神经进化：遗传算法是训练深度神经网络进行强化学习的有竞争力替代方案"。arXiv:1712.06567 [cs.NE]。
  164. "人工智能可以‘进化’解决问题"。《科学 | AAAS》。2018 年 1 月 10 日。2021 年 12 月 9 日存档。2018 年 2 月 7 日检索。
  165. Turchetti C (2004)。《神经网络的随机模型》，《人工智能前沿与应用：基于知识的智能工程系统》，第 102 卷，IOS 出版社，ISBN 978-1-58603-388-0。
  166. Jospin LV, Laga H, Boussaid F, Buntine W, Bennamoun M (2022)。"实践指南：贝叶斯神经网络教程——深度学习用户的学习手册"。《IEEE 计算智能杂志》。第 17 卷，第 2 期。第 29–48 页。arXiv:2007.06823。doi:10.1109/mci.2022.3155327。ISSN 1556-603X。S2CID 220514248。
  167. de Rigo, D., Castelletti, A., Rizzoli, A. E., Soncini-Sessa, R., Weber, E. (2005 年 1 月)。"一种选择性改进技术，用于加快水资源网络管理中的神经动态规划"。在 Pavel Zítek（编）《第 16 届 IFAC 世界大会论文集 – IFAC-PapersOnLine》中的论文。第 16 届 IFAC 世界大会。第 16 卷。捷克布拉格：IFAC。第 7–12 页。doi:10.3182/20050703-6-CZ-1902.02172。hdl:11311/255236。ISBN 978-3-902661-75-3。2012 年 4 月 26 日存档。2011 年 12 月 30 日检索。
  168. Ferreira C (2006)。"使用基因表达编程设计神经网络"。在 A. Abraham, B. de Baets, M. Köppen, B. Nickolay（编）《应用软计算技术：复杂性的挑战》（PDF）中。Springer-Verlag 出版社，第 517–536 页。2013 年 12 月 19 日存档。2012 年 10 月 8 日检索。
  169. Da, Y., Xiurun, G. (2005 年 7 月)。"基于粒子群优化技术与模拟退火的改进 PSO-ANN"。在 T. Villmann（编）《神经计算的新视角：第 11 届欧洲人工神经网络研讨会》中。第 63 卷。Elsevier 出版社，第 527–533 页。doi:10.1016/j.neucom.2004.07.002。2012 年 4 月 25 日存档。2011 年 12 月 30 日检索。
  170. Wu, J., Chen, E. (2009 年 5 月)。"基于粒子群优化技术与人工神经网络的降水预测的新型非参数回归集成方法"。在 Wang, H., Shen, Y., Huang, T., Zeng, Z.（编）《第 6 届国际神经网络研讨会 ISNN 2009》中的论文。Lecture Notes in Computer Science。第 5553 卷。Springer 出版社，第 49–58 页。doi:10.1007/978-3-642-01513-7_6。ISBN 978-3-642-01215-0。2014 年 12 月 31 日存档。2012 年 1 月 1 日检索。
  171. Ting Qin, Zonghai Chen, Haitao Zhang, Sifu Li, Wei Xiang, Ming Li (2004)。"基于 RLS 的 CMAC 学习算法"（PDF）。《神经处理通讯》。19 (1)：49–61。doi:10.1023/B:NEPL.0000016847.18175.60。S2CID 6233899。2021 年 4 月 14 日存档（PDF）。2019 年 1 月 30 日检索。
  172. Ting Qin, Haitao Zhang, Zonghai Chen, Wei Xiang (2005)。"连续 CMAC-QRLS 及其系统阵列"（PDF）。《神经处理通讯》。22 (1)：1–16。doi:10.1007/s11063-004-2694-0。S2CID 16095286。2018 年 11 月 18 日存档（PDF）。2019 年 1 月 30 日检索。
  173. LeCun Y, Boser B, Denker JS, Henderson D, Howard RE, Hubbard W, et al. (1989)。"反向传播应用于手写邮政编码识别"。《神经计算》。1 (4)：541–551。doi:10.1162/neco.1989.1.4.541。S2CID 41312633。
  174. Yann LeCun (2016)。"深度学习在线幻灯片"，2016 年 4 月 23 日存档于 Wayback Machine。
  175. Hochreiter S, Schmidhuber J (1997 年 11 月 1 日)。"长短时记忆"。《神经计算》。9 (8)：1735–1780。doi:10.1162/neco.1997.9.8.1735。ISSN 0899-7667。PMID 9377276。S2CID 1915014。
  176. Sak H, Senior A, Beaufays F (2014)。"用于大规模声学建模的长短时记忆递归神经网络架构"（PDF）。2018 年 4 月 24 日存档。
  177. Li X, Wu X (2014 年 10 月 15 日)。"构建基于长短时记忆的深度递归神经网络用于大词汇量语音识别"。arXiv:1410.4281 [cs.CL]。
  178. Fan Y, Qian Y, Xie F, Soong FK (2014)。"基于双向 LSTM 的递归神经网络的 TTS 合成"。《国际语音通信协会年会论文集，Interspeech》：1964–1968。2017 年 6 月 13 日检索。
  179. Schmidhuber J (2015)。"深度学习"。《学者百科全书》。10 (11)：85–117。Bibcode:2015SchpJ..1032832S。doi:10.4249/scholarpedia.32832。
  180. Zen H, Sak H (2015)。"单向长短时记忆递归神经网络与递归输出层用于低延迟语音合成"（PDF）。Google.com。ICASSP。第 4470–4474 页。2021 年 5 月 9 日存档（PDF）。2017 年 6 月 27 日检索。
  181. Pasick A (2023 年 3 月 27 日)。"人工智能词汇表：神经网络和其他术语解析"。《纽约时报》。ISSN 0362-4331。2023 年 9 月 1 日存档。2023 年 4 月 22 日检索。
  182. Schechner S (2017 年 6 月 15 日)。"Facebook 加强人工智能技术以封锁恐怖分子宣传"。《华尔街日报》。ISSN 0099-9660。2024 年 5 月 19 日存档。2017 年 6 月 16 日检索。
  183. Ciaramella A, Ciaramella M (2024)。《人工智能导论：从数据分析到生成式 AI》。Intellisemantic 出版社。ISBN 978-8-8947-8760-3。
  184. Ganesan N (2010)。"神经网络在使用人口数据诊断癌症中的应用"。《国际计算机应用杂志》。1 (26)：81–97。Bibcode:2010IJCA....1z..81G。doi:10.5120/476-783。
  185. Bottaci L (1997)。"应用人工神经网络预测结直肠癌患者在不同机构中的预后"（PDF）。《柳叶刀》。350 (9076)。柳叶刀：469–472。doi:10.1016/S0140-6736(96)11196-X。PMID 9274582。S2CID 18182063。2018 年 11 月 23 日存档（PDF）。2012 年 5 月 2 日检索。
  186. Alizadeh E, Lyons SM, Castle JM, Prasad A (2016)。"使用 Zernike 矩测量侵袭性癌细胞形状的系统变化"。《综合生物学》。8 (11)：1183–1193。doi:10.1039/C6IB00100A。PMID 27735002。2024 年 5 月 19 日存档。2017 年 3 月 28 日检索。
  187. Lyons S (2016)。"细胞形状变化与小鼠转移潜力的相关性"。《生物学开放》。5 (3)：289–299。doi:10.1242/bio.013409。PMC 4810736。PMID 26873952。
  188. Nabian MA, Meidani H (2017 年 8 月 28 日)。"深度学习在基础设施网络可靠性分析加速中的应用"。《计算机辅助土木与基础设施工程》。33 (6)：443–458。arXiv:1708.08551。Bibcode:2017arXiv170808551N。doi:10.1111/mice.12359。S2CID 36661983。
  189. Nabian MA, Meidani H (2018)。"通过基于机器学习的代理加速地震后交通网络连通性的随机评估"。《交通研究委员会第 97 届年会》。2018 年 3 月 9 日存档。2018 年 3 月 14 日检索。
  190. Díaz E, Brotons V, Tomás R (2018 年 9 月)。"利用人工神经网络预测斜坡岩床上基础的三维弹性沉降"。《土壤与基础》。58 (6)：1414–1422。Bibcode:2018SoFou..58.1414D。doi:10.1016/j.sandf.2018.08.001。hdl:10045/81208。ISSN 0038-0806。
  191. Tayebiyan A, Mohammad TA, Ghazali AH, Mashohor S. "基于人工神经网络的降雨径流建模"。《Pertanika 科学与技术期刊》。24 (2)：319–330。2023 年 5 月 17 日存档。2023 年 5 月 17 日检索。
  192. Govindaraju RS (2000 年 4 月 1 日)。"水文学中的人工神经网络 I：初步概念"。《水文工程学杂志》。5 (2)：115–123。doi:10.1061/(ASCE)1084-0699(2000)5:2(115)。
  193. Govindaraju RS (2000 年 4 月 1 日)。"水文学中的人工神经网络 II：水文学应用"。《水文工程学杂志》。5 (2)：124–137。doi:10.1061/(ASCE)1084-0699(2000)5:2(124)。
  194. Peres DJ, Iuppa C, Cavallaro L, Cancelliere A, Foti E (2015 年 10 月 1 日)。"通过神经网络和重分析风数据扩展显著波高记录"。《海洋建模》。94：128–140。Bibcode:2015OcMod..94..128P。doi:10.1016/j.ocemod.2015.08.002。
  195. Dwarakish GS, Rakshith S, Natesan U (2013)。"神经网络在海岸工程中的应用综述"。《人工智能系统与机器学习》。5 (7)：324–331。2017 年 8 月 15 日存档。2017 年 7 月 5 日检索。
  196. Ermini L, Catani F, Casagli N (2005 年 3 月 1 日)。"应用人工神经网络进行滑坡易发性评估"。《地貌学》。山区环境中的地貌灾害与人类影响。66 (1)：327–343。Bibcode:2005Geomo..66..327E。doi:10.1016/j.geomorph.2004.09.025。
  197. Nix R, Zhang J (2017 年 5 月)。"使用深度神经网络对 Android 应用程序和恶意软件进行分类"。2017 年国际联合神经网络会议（IJCNN）。第 1871–1878 页。doi:10.1109/IJCNN.2017.7966078。ISBN 978-1-5090-6182-2。S2CID 8838479。
  198. "检测恶意网址"。加州大学圣地亚哥分校系统与网络组。2019 年 7 月 14 日存档。2019 年 2 月 15 日检索。
  199. Homayoun S, Ahmadzadeh M, Hashemi S, Dehghantanha A, Khayami R (2018)，Dehghantanha A, Conti M, Dargahi T（编），"BoTShark：一种深度学习方法用于检测僵尸网络流量"，《网络威胁情报》，《信息安全进展》，第 70 卷，Springer 国际出版，第 137–153 页，doi:10.1007/978-3-319-73951-9_7，ISBN 978-3-319-73951-9
  200. Ghosh, Reilly (1994 年 1 月)。"信用卡欺诈检测与神经网络"。《第二十七届夏威夷国际系统科学会议 HICSS-94》。第 3 卷，第 621–630 页。doi:10.1109/HICSS.1994.323314。ISBN 978-0-8186-5090-1。S2CID 13260377。
  201. Ananthaswamy A (2021 年 4 月 19 日)。"最新的神经网络比以往更快地解决世界上最难的方程式"。《量子杂志》。2024 年 5 月 19 日存档。2021 年 5 月 12 日检索。
  202. "人工智能破解了理解我们世界的关键数学难题"。《MIT 技术评论》。2024 年 5 月 19 日存档。2020 年 11 月 19 日检索。
  203. "加州理工学院开源用于求解偏微分方程的人工智能"。《InfoQ》。2021 年 1 月 25 日存档。2021 年 1 月 20 日检索。
  204. Nagy A (2019 年 6 月 28 日)。"具有神经网络假设的变分量子蒙特卡洛方法用于开放量子系统"。《物理评论快报》。122 (25)：250501。arXiv:1902.09483。Bibcode:2019PhRvL.122y0501N。doi:10.1103/PhysRevLett.122.250501。PMID 31347886。S2CID 119074378。
  205. Yoshioka N, Hamazaki R (2019 年 6 月 28 日)。"为开放量子多体系统构建神经站态"。《物理评论 B》。99 (21)：214306。arXiv:1902.07006。Bibcode:2019PhRvB..99u4306Y。doi:10.1103/PhysRevB.99.214306。S2CID 119470636。
  206. Hartmann MJ, Carleo G (2019 年 6 月 28 日)。"神经网络方法用于耗散量子多体动力学"。《物理评论快报》。122 (25)：250502。arXiv:1902.05131。Bibcode:2019PhRvL.122y0502H。doi:10.1103/PhysRevLett.122.250502。PMID 31347862。S2CID 119357494。
  207. Vicentini F, Biella A, Regnault N, Ciuti C (2019 年 6 月 28 日)。"用于开放量子系统稳态的变分神经网络假设"。《物理评论快报》。122 (25)：250503。arXiv:1902.10104。Bibcode:2019PhRvL.122y0503V。doi:10.1103/PhysRevLett.122.250503。PMID 31347877。S2CID 119504484。
  208. Forrest MD (2015 年 4 月)。"基于详细的 Purkinje 神经元模型和一个运行速度超过 400 倍更快的简化代理模型的酒精作用模拟"。《BMC 神经科学》。16 (27)：27。doi:10.1186/s12868-015-0162-6。PMC 4417229。PMID 25928094。
  209. Wieczorek S, Filipiak D, Filipowska A (2018)。"基于神经网络的用户兴趣语义图像分析"。《语义网络研究》。36（语义技术的前沿话题）。doi:10.3233/978-1-61499-894-5-179。2024 年 5 月 19 日存档。2024 年 1 月 20 日检索。
  210. Merchant A, Batzner S, Schoenholz SS, Aykol M, Cheon G, Cubuk ED (2023 年 12 月)。"大规模深度学习用于材料发现"。《自然》。624 (7990)：80–85。Bibcode:2023Natur.624...80M。doi:10.1038/s41586-023-06735-9。ISSN 1476-4687。PMC 10700131。PMID 38030720。
  211. Siegelmann H, Sontag E (1991)。"神经网络中的图灵可计算性"（PDF）。《应用数学快报》。4 (6)：77–80。doi:10.1016/0893-9659(91)90080-F。2024 年 5 月 19 日存档。2017 年 1 月 10 日检索。
  212. Bains S (1998 年 11 月 3 日)。"模拟计算机超越图灵模型"。《EE Times》。2023 年 5 月 11 日存档。2023 年 5 月 11 日检索。
  213. Balcázar J (1997 年 7 月)。"神经网络的计算能力：Kolmogorov 复杂度表征"。《IEEE 信息理论汇刊》。43 (4)：1175–1183。CiteSeerX 10.1.1.411.7782。doi:10.1109/18.605580。
  214. MacKay DJ (2003)。《信息理论、推断与学习算法》 (PDF)。剑桥大学出版社。ISBN 978-0-521-64298-9。2016 年 10 月 19 日存档 (PDF)。2016 年 6 月 11 日检索。
  215. Cover T (1965)。"线性不等式系统的几何和统计特性及其在模式识别中的应用"（PDF）。《IEEE 电子计算机汇刊》。EC-14 (3)。IEEE：326–334。doi:10.1109/PGEC.1965.264137。2016 年 3 月 5 日存档 (PDF)。2020 年 3 月 10 日检索。
  216. Gerald F (2019)。"音频和多媒体数据机器学习的可重复性与实验设计"。《第 27 届 ACM 国际多媒体会议论文集》。ACM。第 2709–2710 页。doi:10.1145/3343031.3350545。ISBN 978-1-4503-6889-6。S2CID 204837170。
  217. "停止摆弄，开始测量！神经网络实验的可预测实验设计"。《Tensorflow Meter》。2022 年 4 月 18 日存档。2020 年 3 月 10 日检索。
  218. Lee J, Xiao L, Schoenholz SS, Bahri Y, Novak R, Sohl-Dickstein J, 等人 (2020)。"任何深度的宽神经网络在梯度下降下演化为线性模型"。《统计力学杂志：理论与实验》。2020 (12)：124002。arXiv:1902.06720。Bibcode:2020JSMTE2020l4002L。doi:10.1088/1742-5468/abc62b。S2CID 62841516。
  219. Arthur Jacot, Franck Gabriel, Clement Hongler (2018)。《神经切线核：神经网络中的收敛性与泛化》 (PDF)。第 32 届神经信息处理系统会议（NeurIPS 2018），蒙特利尔，加拿大。2022 年 6 月 22 日存档 (PDF)。2022 年 6 月 4 日检索。
  220. Xu ZJ, Zhang Y, Xiao Y (2019)。"深度神经网络在频域中的训练行为"。在 Gedeon T, Wong K, Lee M（编）《神经信息处理》一书中。计算机科学讲义笔记。第 11953 卷。Springer，Cham。第 264–274 页。arXiv:1807.01251。doi:10.1007/978-3-030-36708-4_22。ISBN 978-3-030-36707-7。S2CID 49562099。
  221. Nasim Rahaman, Aristide Baratin, Devansh Arpit, Felix Draxler, Min Lin, Fred Hamprecht, 等人 (2019)。"神经网络的频谱偏差"（PDF）。《第 36 届国际机器学习会议论文集》。97：5301–5310。arXiv:1806.08734。2022 年 10 月 22 日存档 (PDF)。2022 年 6 月 4 日检索。
  222. Zhi-Qin John Xu, Yaoyu Zhang, Tao Luo, Yanyang Xiao, Zheng Ma (2020)。"频率原理：傅里叶分析揭示深度神经网络"。《计算物理通讯》。28 (5)：1746–1767。arXiv:1901.06523。Bibcode:2020CCoPh..28.1746X。doi:10.4208/cicp.OA-2020-0085。S2CID 58981616。
  223. Tao Luo, Zheng Ma, Zhi-Qin John Xu, Yaoyu Zhang (2019)。"一般深度神经网络的频率原理理论"。arXiv:1906.09235 [cs.LG]。
  224. Xu ZJ, Zhou H (2021 年 5 月 18 日)。"深度频率原理：理解为什么更深的学习更快"。《AAAI 人工智能会议论文集》。35 (12)：10541–10550。arXiv:2007.14313。doi:10.1609/aaai.v35i12.17261。ISSN 2374-3468。S2CID 220831156。2021 年 10 月 5 日存档。2021 年 10 月 5 日检索。
  225. Parisi GI, Kemker R, Part JL, Kanan C, Wermter S (2019
  226. Dean Pomerleau, "基于知识的人工神经网络训练用于自主机器人驾驶"
  227. Dewdney AK (1997 年 4 月 1 日). *Yes, we have no neutrons: an eye-opening tour through the twists and turns of bad science*. Wiley. 第 82 页. ISBN 978-0-471-10806-1.
  228. NASA – Dryden Flight Research Center – 新闻室: *新闻发布：NASA 神经网络项目通过了里程碑*。2010 年 4 月 2 日通过 Wayback Machine 存档。Nasa.gov. 2013 年 11 月 20 日检索。 "Roger Bridgman 对神经网络的辩护"。2012 年 3 月 19 日存档。2010 年 7 月 12 日检索。 "Scaling Learning Algorithms towards AI – LISA – Publications – Aigaion 2.0"。iro.umontreal.ca。
  229. D. J. Felleman 和 D. C. Van Essen，“灵长类动物大脑皮层中的分布式层次处理”，*Cerebral Cortex*, 1, 第 1–47 页，1991 年。
  230. J. Weng，“自然与人工智能：计算大脑-心智导论”（2012 年 5 月 19 日存档），BMI 出版社，ISBN 978-0-9858757-2-5，2012 年。
  231. Edwards C (2015 年 6 月 25 日). "深度学习的成长烦恼"。*ACM 通讯*，58 (7): 14–16。doi:10.1145/2771283. S2CID 11026540。 "苦涩的教训"。incompleteideas.net. 2024 年 8 月 7 日检索。
  232. Cade Metz (2016 年 5 月 18 日). "谷歌为其 AI 机器人打造了自己的芯片"。*Wired*。2018 年 1 月 13 日存档。2017 年 3 月 5 日检索。 "Scaling Learning Algorithms towards AI"（PDF）。2022 年 8 月 12 日存档。2022 年 7 月 6 日检索。
  233. Tahmasebi, Hezarkhani (2012). "一种用于等级估算的混合神经网络-模糊逻辑-遗传算法"。*Computers & Geosciences*，42: 18–27。Bibcode:2012CG.....42...18T。doi:10.1016/j.cageo.2012.02.004。PMC 4268588。PMID 25540468。
  234. Sun 和 Bookman，1990 年。
  235. Norori N, Hu Q, Aellen FM, Faraci FD, Tzovara A (2021 年 10 月). "解决大数据和人工智能在医疗中的偏见问题：呼吁开放科学"。*Patterns*，2 (10): 100347。doi:10.1016/j.patter.2021.100347。PMC 8515002。PMID 34693373。
  236. Carina W (2022 年 10 月 27 日). "面部识别技术的偏见对刑事司法中的种族歧视的影响"。*Scientific and Social Research*，4 (10): 29–40。doi:10.26689/ssr.v4i10.4402。ISSN 2661-4332。
  237. Chang X (2023 年 9 月 13 日). "招聘中的性别偏见：对亚马逊招聘算法影响的分析"。*Advances in Economics, Management and Political Sciences*，23 (1): 134–140。doi:10.54254/2754-1169/23/20230367。ISSN 2754-1169。2023 年 12 月 9 日存档，2023 年 12 月 9 日检索。
  238. Kortylewski A, Egger B, Schneider A, Gerig T, Morel-Forster A, Vetter T (2019 年 6 月). "通过合成数据分析和减少数据集偏见对面部识别的损害"。2019 年 IEEE/CVF 计算机视觉与模式识别研讨会（CVPRW）(PDF)，IEEE，第 2261–2268 页。doi:10.1109/cvprw.2019.00279。ISBN 978-1-7281-2506-0。S2CID 198183828。2024 年 5 月 19 日存档，2023 年 12 月 30 日检索。
  239. Huang Y (2009). "人工神经网络的进展——方法学发展与应用"。*Algorithms*，2 (3): 973–1007。doi:10.3390/algor2030973。ISSN 1999-4893。
  240. Kariri E, Louati H, Louati A, Masmoudi F (2023). "探索人工神经网络的进展与未来研究方向：一种文本挖掘方法"。*Applied Sciences*，13 (5): 3186。doi:10.3390/app13053186。ISSN 2076-3417。
  241. Fui-Hoon Nah F, Zheng R, Cai J, Siau K, Chen L (2023 年 7 月 3 日). "生成性 AI 与 ChatGPT：应用、挑战与 AI-人类合作"。*Journal of Information Technology Case and Application Research*，25 (3): 277–304。doi:10.1080/15228053.2023.2233814。ISSN 1522-8053。 "DALL-E 2 的失败是它最有趣的部分 – IEEE Spectrum"。IEEE。2022 年 7 月 15 日存档，2023 年 12 月 9 日检索。
  242. Briot JP (2021 年 1 月). "从人工神经网络到深度学习在音乐生成中的应用：历史、概念与趋势"。*Neural Computing and Applications*，33 (1): 39–65。doi:10.1007/s00521-020-05399-0。ISSN 0941-0643。
  243. Chow PS (2020 年 7 月 6 日). "机器中的鬼魂（好莱坞机器）：人工智能在电影行业的出现性应用"。*NECSUS_European Journal of Media Studies*。doi:10.25969/MEDIAREP/14307。ISSN 2213-0217。
  244. Yu X, He S, Gao Y, Yang J, Sha L, Zhang Y, 等人 (2010 年 6 月). "为视频游戏《Dead-End》动态调整游戏 AI 难度"。第三届国际信息科学与交互科学会议，IEEE，第 583–587 页。doi:10.1109/icicis.2010.5534761。ISBN 978-1-4244-7384-7。S2CID 17555595。

14. 参考文献

15. 外部链接

                     

© 小时科技 保留一切权利