切比雪夫多项式（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：第一类切比雪夫多项式 $T_n$ 的前五项绘图

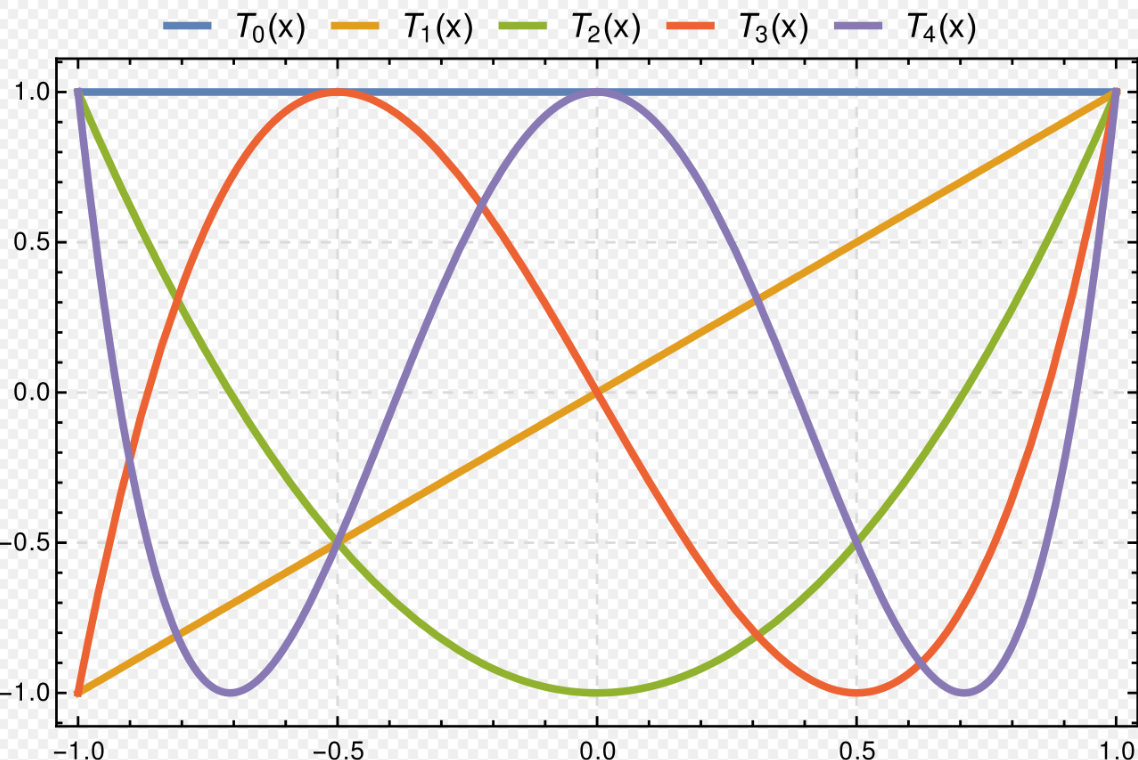
　　 切比雪夫多项式是两组与余弦函数和正弦函数相关的正交多项式，分别记作 $T_n(x)$ 和 $U_n(x)$。它们有多种等价定义方式，其中一种起始于三角函数的表示：

　　 第一类切比雪夫多项式 $T_n$ 定义为： $$ T_n(\cos \theta) = \cos\left(n\theta\right) ~ $$ 类似地，第二类切比雪夫多项式 $U_n$ 定义为： $$ U_n(\cos \theta)\sin \theta = \sin\left((n+1)\theta\right) ~ $$ 乍一看，这些表达式是否真的定义了关于 $\cos \theta$ 的多项式并不明显，但可以通过莫阿弗公式（de Moivre’s formula）来证明这一点（见下文）。

图
图 2：第二类切比雪夫多项式 $U_n$ 的前五个多项式图像

　　 切比雪夫多项式 $T_n$ 是在区间 $[-1, 1]$ 上绝对值被限制在 1 以内、且首项系数最大的多项式。它们也是满足许多其他性质的 “极值” 多项式之一 \(^\text{[1]}\)。

　　 1952 年，科尔内利乌斯·兰齐奥斯指出，切比雪夫多项式在线性系统求解的逼近理论中具有重要作用 \(^\text{[2]}\)；$T_n(x)$ 的根，也称为切比雪夫节点，被用作多项式插值中的匹配点，从而优化插值过程。由此得到的插值多项式能够减小龙格现象的问题，并在最大范数意义下提供接近最佳的函数逼近，这也称为 “极小极大” 准则。这种逼近直接引出了克伦肖–柯蒂斯求积法的方法。

　　 这些多项式以帕夫努季·切比雪夫的名字命名 \(^\text{[3]}\)。使用字母 $T$ 是因为该名字的其他音译方式，如法语的 Tchebycheff、Tchebyshev，或德语的 Tschebyschow。

1. 定义

递推定义

　　 第一类切比雪夫多项式 $T_n(x)$ 可由以下递推关系定义： $$ \begin{aligned} T_0(x) &= 1, \\ T_1(x) &= x, \\ T_{n+1}(x) &= 2x \, T_n(x) - T_{n-1}(x). \end{aligned}~ $$ 第二类切比雪夫多项式 $U_n(x)$ 可由以下递推关系定义： $$ \begin{aligned} U_0(x) &= 1, \\ U_1(x) &= 2x, \\ U_{n+1}(x) &= 2x \, U_n(x) - U_{n-1}(x), \end{aligned}~ $$ 这个递推关系与第一类切比雪夫多项式的定义几乎相同，仅在 $n = 1$ 时的初始值规则上有所不同。

三角定义

　　 第一类与第二类切比雪夫多项式可以定义为满足以下关系的唯一多项式： $$ T_n(\cos \theta) = \cos\left(n\theta\right) ~ $$ 以及 $$ U_n(\cos \theta) = \frac{ \sin\left((n+1)\theta\right) }{\sin \theta},~ $$ 其中 $n = 0, 1, 2, 3, \ldots$。

　　 另一种等价的表述方式是利用复数的幂形式：设复数 $z = a + bi$，其模为 1，则有 $$ z^n = T_n(a) + i b U_{n-1}(a)~ $$ 当研究三角多项式时，切比雪夫多项式可以采用这种形式定义 \(^\text{[4]}\)。

　　 可以通过以下观察说明 $ \cos\left(nx\right) $ 是 $ \cos\left(x\right) $ 的 $n$ 次多项式：$ \cos\left(nx\right) $ 是下式左边的实部，这是德·莫弗公式（de Moivre’s formula）： $$ \cos\left(n\theta\right) + i \sin\left(n\theta\right) = (\cos \theta + i \sin \theta)^n~ $$ 该等式右边的实部是 $ \cos\left(x\right) $ 与 $ \sin\left(x\right) $ 的多项式，其中 $ \sin\left(x\right) $ 的幂次均为偶数，因此可利用恒等式 $$ \cos^2(x) + \sin^2(x) = 1~ $$ 将所有 $ \sin\left(x\right) $ 的幂次项替换为 $ \cos\left(x\right) $ 的表达式。类似地，$ \sin\left(nx\right) $ 是该多项式的虚部，虚部中的 $ \sin\left(x\right) $ 的幂次均为奇数，若提取出一个 $ \sin\left(x\right) $ 因子，则其余部分就可以转换为一个关于 $ \cos\left(x\right) $ 的 $n-1$ 次多项式。

　　 对于 $x$ 在区间 $[-1, 1]$ 之外的情况，上述定义意味着： $$ T_n(x) = \begin{cases} \cos\left(n \arccos x\right) & \text{如果 } |x| \leq 1, \\ \cosh\left(n \, \mathrm{arcosh}\, x\right) & \text{如果 } x \geq 1, \\ (-1)^n \cosh\left(n \, \mathrm{arcosh}(-x)\right) & \text{如果 } x \leq -1 \end{cases}~ $$

可交换多项式定义

　　 切比雪夫多项式还可以通过以下定理来刻画：\(^\text{[5]}\)

　　 若 $F_n(x)$ 是一族在特征为 0 的域上的一元首一多项式族，满足：$\deg F_n(x) = n$，以及对所有 $m$ 和 $n$ 都有 $F_m(F_n(x)) = F_n(F_m(x))$，

　　 那么，经过一个简单的变量变换之后，要么 $$ F_n(x) = x^n \quad \text{对所有 } n~ $$ 要么 $$ F_n(x) = 2 \cdot T_n(x/2) \quad \text{对所有 } n~ $$

Pell 方程定义

　　 切比雪夫多项式还可以定义为以下 Pell 方程在环 $R[x]$ \(^\text{[6]}\) 中的解： $$ T_n(x)^2 - (x^2 - 1) U_{n-1}(x)^2 = 1~ $$ 因此，它们也可以通过 Pell 方程的标准解法生成，即从基本解出发取幂： $$ T_n(x) + U_{n-1}(x) \sqrt{x^2 - 1} = \left(x + \sqrt{x^2 - 1}\right)^n~ $$

生成函数

　　 切比雪夫多项式 $T_n$ 的普通生成函数为： $$ \sum_{n=0}^{\infty} T_n(x)\, t^n = \frac{1 - t x}{1 - 2 t x + t^2}~ $$ 切比雪夫多项式还有多个其他形式的生成函数。其中，指数生成函数为： $$ \begin{aligned} \sum_{n=0}^{\infty} T_n(x)\, \frac{t^n}{n!} &= \frac{1}{2} \left( \exp\left(t \left(x - \sqrt{x^2 - 1} \right)\right)+ \exp\left(t \left(x + \sqrt{x^2 - 1} \right)\right) \right)\\ &= e^{t x} \cosh\left(t \sqrt{x^2 - 1}\right)\\ \end{aligned}~ $$ 在二维势场理论和多极展开中，相关的生成函数为： $$ \sum_{n=1}^{\infty} T_n(x)\, \frac{t^n}{n} = \ln \left( \frac{1}{\sqrt{1 - 2 t x + t^2}} \right)~ $$ 切比雪夫第二类多项式 $U_n$ 的**普通生成函数**为： $$ \sum_{n=0}^{\infty} U_n(x)\, t^n = \frac{1}{1 - 2 t x + t^2}~ $$ 其指数生成函数为： $$ \sum_{n=0}^{\infty} U_n(x)\, \frac{t^n}{n!} = e^{t x} \left( \cosh\left(t \sqrt{x^2 - 1}\right) + \frac{x}{\sqrt{x^2 - 1}} \sinh\left(t \sqrt{x^2 - 1}\right) \right)~ $$

2. 第一类与第二类切比雪夫多项式之间的关系

　　 第一类和第二类切比雪夫多项式分别对应于参数为 $P = 2x$、$Q = 1$ 的一对互补的 Lucas 数列 $\tilde{V}_n(P, Q)$ 和 $\tilde{U}_n(P, Q)$： $$ \begin{aligned} \tilde{U}_n(2x, 1) &= U_{n-1}(x), \\ \tilde{V}_n(2x, 1) &= 2 T_n(x). \end{aligned}~ $$ 由此可推出它们还满足一组互相关联的递推关系式：\(^\text{[7]}\) $$ \begin{aligned} T_{n+1}(x) &= x\, T_n(x) - (1 - x^2)\, U_{n-1}(x), \\ U_{n+1}(x) &= x\, U_n(x) + T_{n+1}(x) \end{aligned}~ $$ 第二个式子可以通过第二类切比雪夫多项式的递推定义重新整理为： $$ T_n(x) = \frac{1}{2} \left( U_n(x) - U_{n-2}(x) \right)~ $$ 利用该公式迭代展开，可以得到以下求和公式： $$ U_n(x) = \begin{cases} 2 \sum\limits_{\substack{j > 0 \\ j \text{ 奇数}}}^{n} T_j(x) & \text{当 } n \text{ 为奇数时}, \\ 2 \sum\limits_{\substack{j \geq 0 \\ j \text{ 偶数}}}^{n} T_j(x) - 1 & \text{当 } n \text{ 为偶数时} \end{cases}~ $$ 这表明第二类切比雪夫多项式可以表示为第一类切比雪夫多项式的加权和。

　　 通过使用 $T_n(x)$ 的导数公式替换 $U_n(x)$  和 $U_{n-2}(x)$，可以得到 $T_n(x)$ 导数的递推关系式： $$ 2\,T_n(x) = \frac{1}{n+1} \frac{d}{dx} T_{n+1}(x) - \frac{1}{n-1} \frac{d}{dx} T_{n-1}(x), \quad n = 2, 3, \ldots~ $$ 这个关系式被用于切比雪夫谱方法中以求解微分方程。

　　 图兰不等式对于切比雪夫多项式为：\(^\text{[8]}\) $$ \begin{aligned} T_n(x)^2 - T_{n-1}(x)\,T_{n+1}(x) &= 1 - x^2 > 0, & \text{当 } -1 < x < 1, \\ U_n(x)^2 - U_{n-1}(x)\,U_{n+1}(x) &= 1 > 0 \end{aligned}~ $$ 积分关系式如下所示：\(^\text{[9][10]}\) $$ \begin{aligned} \int_{-1}^{1} \frac{T_n(y)}{y - x} \cdot \frac{dy}{\sqrt{1 - y^2}} &= \pi\, U_{n-1}(x), \\ \int_{-1}^{1} \frac{U_{n-1}(y)}{y - x} \cdot \sqrt{1 - y^2}\,dy &= -\pi\, T_n(x), \end{aligned}~ $$ 其中积分以主值积分的方式计算。

3. 显式表达式

　　 使用复数幂定义的切比雪夫多项式，可以推导出以下在任意实数 $x$ 上成立的表达式：\ $$ \begin{aligned} T_n(x) &= \frac{1}{2} \left( \left(x - \sqrt{x^2 - 1} \right)^n + \left(x + \sqrt{x^2 - 1} \right)^n \right) \\ &= \frac{1}{2} \left( \left(x - \sqrt{x^2 - 1} \right)^n + \left(x - \sqrt{x^2 - 1} \right)^{-n} \right) \end{aligned}~ $$ 这两个公式是等价的，因为 $$ \left(x + \sqrt{x^2 - 1} \right)\left(x - \sqrt{x^2 - 1} \right) = 1~ $$ 根据 de Moivre 公式，可以得到切比雪夫多项式的一个按幂次 $x^k$ 展开的显式形式： $$ T_n(\cos \theta) = \operatorname{Re}(\cos n\theta + i\sin n\theta) = \operatorname{Re}((\cos \theta + i \sin \theta)^n)~ $$ 其中 $\operatorname{Re}$ 表示复数的实部。展开这个公式得到： $$ (\cos \theta + i \sin \theta)^n = \sum_{j=0}^{n} \binom{n}{j} i^j \sin^j \theta \cos^{n-j} \theta~ $$ 该表达式的实部来自于偶数下标项。注意到 $i^{2j} = (-1)^j$，以及 $\sin^{2j} \theta = (1 - \cos^2 \theta)^j$，可以得到如下显式公式： $$ \cos\left(n\theta\right) = \sum_{j = 0}^{\lfloor n/2 \rfloor} \binom{n}{2j} (\cos^2 \theta - 1)^j \cos^{n - 2j} \theta~ $$ 这进一步意味着： $$ T_n(x) = \sum_{j = 0}^{\lfloor n/2 \rfloor} \binom{n}{2j} (x^2 - 1)^j x^{n - 2j}~ $$ 这可以表示为一个 ${}_2F_1$ 超几何函数： $$ \begin{aligned} T_n(x) &= \sum_{k=0}^{\left\lfloor \frac{n}{2} \right\rfloor}\binom{n}{2k}(x^2 - 1)^k x^{n - 2k}\\ &= x^n \sum_{k=0}^{\left\lfloor \frac{n}{2} \right\rfloor} \binom{n}{2k}(1 - x^{-2})^k\\ &= \frac{n}{2} \sum_{k=0}^{\left\lfloor \frac{n}{2} \right\rfloor} (-1)^k \frac{(n-k-1)!}{k!(n-2k)!}(2x)^{n - 2k} \quad \text{（当 } n > 0 \text{ 时）}\\ &= n \sum_{k=0}^{n} (-2)^k \frac{(n+k-1)!}{(n-k)!(2k)!} (1 - x)^k \quad \text{（当 } n > 0 \text{ 时）}\\ &= {}_2F_1 \left( -n, n; \frac{1}{2}; \frac{1}{2}(1 - x) \right) \end{aligned}~ $$ 带有反函数 \(^\text{[11][12]}\)： $$ x^n = 2^{1 - n} \mathop{\sum_{\substack{j = 0 \\ j \equiv n \bmod 2}}^{n}}' \binom{n}{\tfrac{n - j}{2}} T_j(x)~ $$ 其中，求和符号上的撇号（′）表示：若求和中出现 $j = 0$，其对应的项需要减半处理。

　　 一个关于 $T_n$ 的相关表达式，可将其表示为带有二项式系数和 2 的幂次的单项式之和： $$ T_n(x) = \sum_{m = 0}^{\left\lfloor \frac{n}{2} \right\rfloor} (-1)^m \left( \binom{n - m}{m} + \binom{n - m - 1}{n - 2m} \right) \cdot 2^{n - 2m - 1} \cdot x^{n - 2m}~ $$ 同样地，$U_n$ 也可以用超几何函数表示为： $$ U_n(x) = \frac{(x + \sqrt{x^2 - 1})^{n+1} - (x - \sqrt{x^2 - 1})^{n+1}}{2\sqrt{x^2 - 1}}~ $$ 它还可以展开为多种等价形式：

　　 二项式展开形式： $$ = \sum_{k=0}^{\left\lfloor n/2 \right\rfloor} \binom{n+1}{2k+1} (x^2 - 1)^k x^{n - 2k}~ $$ 提取 $x^n$ 的因子： $$ = x^n \sum_{k=0}^{\left\lfloor n/2 \right\rfloor} \binom{n+1}{2k+1} \left(1 - x^{-2}\right)^k~ $$ 用带负上下标的组合数写成： $$ = \sum_{k=0}^{\left\lfloor n/2 \right\rfloor} \binom{2k - (n + 1)}{k} (2x)^{n - 2k}, \quad \text{当 } n > 0~ $$ 用交错符号的组合数写成： $$ = \sum_{k=0}^{\left\lfloor n/2 \right\rfloor} (-1)^k \binom{n - k}{k} (2x)^{n - 2k}, \quad \text{当 } n > 0~ $$ 用阶乘和幂级数形式表示： $$ = \sum_{k=0}^{n} (-2)^k \cdot \frac{(n + k + 1)!}{(n - k)! (2k + 1)!} (1 - x)^k, \quad \text{当 } n > 0~ $$ 最后可化为超几何函数表达式： $$ = (n + 1) \cdot {}_2F_1\left(-n,\, n + 2;\, \tfrac{3}{2};\, \tfrac{1}{2}(1 - x)\right)~ $$ 其中，${}_2F_1$ 是高斯超几何函数。

4. 性质

对称性

　　 $$ \begin{aligned} T_n(-x) &= (-1)^n\, T_n(x), \\ U_n(-x) &= (-1)^n\, U_n(x). \end{aligned}~ $$ 也就是说，奇偶阶的切比雪夫多项式具有相应的对称性：偶数阶的切比雪夫多项式是偶函数，因此只包含 $x$ 的偶次幂；奇数阶的切比雪夫多项式是奇函数，因此只包含 $x$ 的奇次幂。

零点与极值

　　 任意一种类型、次数为 $n$ 的切比雪夫多项式在区间 $[-1,1]$ 上都有 $n$ 个不同的单根，这些根称为切比雪夫根。其中，第一类切比雪夫多项式（$T_n$）的根有时被称为切比雪夫节点，因为它们常用于多项式插值中的节点选择。

　　 利用三角函数定义以及恒等式： $$ \cos\left((2k + 1)\frac{\pi}{2}\right) = 0,~ $$ 可以得出第一类切比雪夫多项式 $T_n$ 的根为： $$ x_k = \cos\left(\frac{\pi(k + 1/2)}{n}\right),\quad k = 0, 1, \dots, n - 1.~ $$ 类似地，第二类切比雪夫多项式 $U_n$ 的根为： $$ x_k = \cos\left(\frac{k\pi}{n + 1}\right),\quad k = 1, 2, \dots, n.~ $$ 第一类切比雪夫多项式 $T_n$ 在区间 $-1 \leq x \leq 1$ 上的极值点位于： $$ x_k = \cos\left(\frac{k\pi}{n}\right),\quad k = 0, 1, \dots, n.~ $$ 第一类切比雪夫多项式的一个独特性质是：在区间 $-1 \leq x \leq 1$ 上，它的所有极值点的函数值都严格等于 $-1$ 或 $1$。因此，这些多项式仅有两个有限的临界值，这也是 Shabat 多项式的定义性特征。

　　 第一类和第二类切比雪夫多项式在端点处的极值分别为： $$ \begin{aligned} T_n(1) &= 1 \\ T_n(-1) &= (-1)^n \\ U_n(1) &= n + 1 \\ U_n(-1) &= (-1)^n(n + 1) \end{aligned}~ $$ 对于 $n > 0$，第一类切比雪夫多项式 $T_n(x)$ 在区间 $-1 \leq x \leq 1$ 上有 $n + 1$ 个极值点。这些极值点出现在：$\pm1$，或者形如 $\cos\left(\frac{2\pi k}{d}\right)$ 的位置，其中满足条件：$d > 2$，$d$ 整除 $2n$（即 $d \mid 2n$），$0 < k < d/2$，$k$ 与 $d$ 互质（即 $\gcd(k, d) = 1$）。换句话说，极值点的横坐标来自于单位圆上的余弦值，其角度对应的是以 $2\pi \frac{k}{d}$ 分布的点，且这些 $k$ 是与 $d$ 互质的小于 $d/2$ 的整数。

　　 特别地（关于 $2\cos\left(2\pi/n\right)$ 的最小多项式 [13][14]），当 $n$ 为偶数时：

　　 当 $n$ 为奇数时：

导数与积分

　　 切比雪夫多项式的导数形式并不总是直观易得。但通过对其三角形式求导，可以得到以下结果： $$ \begin{aligned} \frac{dT_n}{dx} &= n U_{n-1}, \\ \frac{dU_n}{dx} &= \frac{(n+1)T_{n+1} - xU_n}{x^2 - 1}, \\ \frac{d^2 T_n}{dx^2} &= n \cdot \frac{n T_n - x U_{n-1}}{x^2 - 1} = n \cdot \frac{(n + 1)T_n - U_n}{x^2 - 1}. \end{aligned}~ $$ 上述后两个公式在数值计算中可能存在问题，因为在 $x = \pm 1$ 处会出现 0/0 的不定形式。应用洛必达法则可以得到在边界点的极限值： $$ \begin{aligned} \left.\frac{d^2 T_n}{dx^2}\right|_{x = 1} &= \frac{n^4 - n^2}{3}, \\ \left.\frac{d^2 T_n}{dx^2}\right|_{x = -1} &= (-1)^n \frac{n^4 - n^2}{3}. \end{aligned}~ $$ 更一般地，有： $$ \left.\frac{d^p T_n}{dx^p}\right|_{x = \pm 1} = (\pm 1)^{n + p} \prod_{k = 0}^{p - 1} \frac{n^2 - k^2}{2k + 1},~ $$ 这个公式在数值解特征值问题中非常有用。

　　 此外，还有更一般的导数展开式： $$ \frac{d^p}{dx^p} T_n(x) = 2^p n \sum\nolimits^{\prime}_{\substack{0 \leq k \leq n - p \\ k \equiv n - p \!\!\!\! \pmod{2}}} \binom{\frac{n + p - k}{2} - 1}{\frac{n - p - k}{2}} \frac{\left( \frac{n + p + k}{2} - 1 \right)!}{\left( \frac{n - p + k}{2} \right)!} T_k(x) ,\quad p \geq 1~ $$ 其中：求和中带有撇号（$\sum'$）表示：当 $k = 0$ 项存在时，其系数应当减半；求和变量 $k$ 的取值需满足 $k \equiv n - p \mod 2$，即与 $n - p$ 同奇偶性； 该表达式给出了任意阶导数 $T_n^{(p)}(x)$ 用较低次切比雪夫多项式表示的展开式，常用于解析递推与数值计算。

　　 关于积分：由 $T_n$ 的一阶导数可知： $$ \int U_n\, dx = \frac{T_{n+1}}{n+1}~ $$ 此外，通过涉及导数的第一类切比雪夫多项式的递推关系，可以推导出当 $n \geq 2$ 时： $$ \int T_n\, dx = \frac{1}{2} \left( \frac{T_{n+1}}{n+1} - \frac{T_{n-1}}{n-1} \right) = \frac{n\,T_{n+1}}{n^2 - 1} - \frac{x\,T_n}{n - 1}~ $$ 这个公式还可以进一步化简，只用第一类切比雪夫多项式表示 $T_n$ 的积分： $$ \begin{aligned} \int T_n\, dx &= \frac{n}{n^2 - 1} T_{n+1} - \frac{1}{n - 1} T_1 T_n \\ &= \frac{n}{n^2 - 1} T_{n+1} - \frac{1}{2(n - 1)} (T_{n+1} + T_{n-1}) \\ &= \frac{1}{2(n + 1)} T_{n+1} - \frac{1}{2(n - 1)} T_{n-1} \end{aligned}~ $$ 这些公式在解析计算积分、谱方法与正交展开中具有实际应用价值。

　　 此外，还有： $$ \int_{-1}^{1} T_n(x)\, dx = \begin{cases} \displaystyle \frac{(-1)^n + 1}{1 - n^2}, & \text{如果 } n \neq 1 \\ 0, & \text{如果 } n = 1 \end{cases}~ $$

切比雪夫多项式的乘积

　　 第一类切比雪夫多项式满足如下关系式： $$ T_m(x)\,T_n(x) = \frac{1}{2} \left( T_{m+n}(x) + T_{|m-n|}(x) \right), \quad \forall\, m, n \geq 0~ $$ 这个恒等式可以直接由余弦的积化和公式推导得出： $$ 2\cos \alpha \cos \beta = \cos\left(\alpha + \beta\right) + \cos\left(\alpha - \beta\right) ~ $$ 当 $n = 1$ 时，该公式就等价于我们已知的递推公式，只是排列方式不同；而当 $n = 2$ 时，它就构成了对所有偶数阶或奇数阶切比雪夫多项式的递推关系（取决于较小的 $m$ 的奇偶性），这进一步体现了这些多项式的偶函数或奇函数特性。

　　 由上述乘积展开公式还可推导出三条非常有用的计算公式： $$ \begin{aligned} T_{2n}(x) &= 2T_n^2(x) - T_0(x) = 2T_n^2(x) - 1, \\ T_{2n+1}(x) &= 2T_{n+1}(x) T_n(x) - T_1(x) = 2T_{n+1}(x) T_n(x) - x, \\ T_{2n-1}(x) &= 2T_{n-1}(x) T_n(x) - T_1(x) = 2T_{n-1}(x) T_n(x) - x. \end{aligned}~ $$ 第二类切比雪夫多项式满足类似的乘积关系： $$ T_m(x)\, U_n(x) = \begin{cases} \frac{1}{2} \left( U_{m+n}(x) + U_{n - m}(x) \right), & \text{若 } n \geq m - 1 \\ \frac{1}{2} \left( U_{m+n}(x) - U_{m - n - 2}(x) \right), & \text{若 } n \leq m - 2 \end{cases}~ $$ （按照约定，定义 $U_{-1} \equiv 0$）。

　　 此外还满足以下乘积公式： $$ U_m(x)\, U_n(x) = \sum_{k = 0}^{n} U_{m - n + 2k}(x) = \sum_{\substack{p = m - n \\ \text{步长为 2}}}^{m + n} U_p(x)~ $$ 适用于 $m \geq n$ 的情况。当 $n = 2$ 时，这一递推公式简化为： $$ \begin{aligned} U_{m+2}(x) &= U_2(x) \cdot U_m(x) - U_m(x) - U_{m-2}(x) \\ &= U_m(x) \cdot \left( U_2(x) - 1 \right) - U_{m-2}(x) \end{aligned}~ $$ 这个关系说明了第二类切比雪夫多项式中，偶数或奇数下标的多项式的奇偶性特征，具体取决于 $m$ 是从 2 还是从 3 开始。

复合与可除性性质

　　 第一类和第二类切比雪夫多项式的三角函数定义蕴含了它们的复合（嵌套）性质 \(^\text{[15]}\)： $$ \begin{aligned} T_{mn}(x) &= T_m(T_n(x)), \\ U_{mn - 1}(x) &= U_{m - 1}(T_n(x))U_{n - 1}(x) \end{aligned}~ $$ 对于 $T_{mn}$，复合的顺序是可以交换的，这使得 $T_n$ 构成了一个在复合运算下的交换半群。

　　 由于当 $m$ 为奇数时，$T_m(x)$ 可被 $x$ 整除，因此可以推出：若 $m$ 是奇数，则 $T_{mn}(x)$ 可被 $T_n(x)$ 整除；此外，无论 $m$ 为奇偶，$U_{mn - 1}(x)$ 总是可被 $U_{n - 1}(x)$ 整除；若 $m$ 为偶数，$U_{mn - 1}(x)$ 还可被 $T_n(x) U_{n - 1}(x)$ 整除。

正交性

　　 第一类切比雪夫多项式 $T_n$ 和第二类切比雪夫多项式 $U_n$ 都构成一列正交多项式序列。

　　 其中，第一类多项式 $T_n$ 在区间 $[-1,1]$ 上关于权函数： $$ \frac{1}{\sqrt{1 - x^2}}~ $$ 是正交的，即满足： $$ \int_{-1}^{1} T_n(x) \, T_m(x) \, \frac{dx}{\sqrt{1 - x^2}} = \begin{cases} 0 & \text{若 } n \ne m \\ \pi & \text{若 } n = m = 0 \\ \frac{\pi}{2} & \text{若 } n = m \ne 0 \end{cases}~ $$ 这个正交性可以通过代换 $x = \cos\left(\theta\right) $，并利用定义恒等式：$T_n( \cos\left(\theta\right) ) = \cos\left(n\theta\right) $ 来加以证明。

　　 类似地，第二类切比雪夫多项式 $U_n$ 在区间 $[-1,1]$ 上关于权函数： $$ \sqrt{1 - x^2}~ $$ 也是正交的，即满足： $$ \int_{-1}^{1} U_n(x) \, U_m(x) \, \sqrt{1 - x^2} \, dx = \begin{cases} 0 & \text{若 } n \ne m \\ \frac{\pi}{2} & \text{若 } n = m \end{cases}~ $$ （这个测度 $\sqrt{1 - x^2} \, dx$ 除了一个归一化常数外，就是著名的 Wigner 半圆分布。）

　　 这些正交性源于这样一个事实：切比雪夫多项式是以下切比雪夫微分方程的解： $$ \begin{aligned} (1 - x^2) T_n'' - x T_n' + n^2 T_n &= 0, \\ (1 - x^2) U_n'' - 3x U_n' + n(n + 2) U_n &= 0, \end{aligned}~ $$ 这些都是 Sturm–Liouville 型微分方程，而这类方程的一般性质之一就是它们拥有一组正交归一的解函数组。（事实上，切比雪夫多项式也可以被定义为这些方程的特解。）

　　 第一类切比雪夫多项式 $T_n$ 还满足一个离散正交性条件： $$ \sum_{k = 0}^{N - 1} T_i(x_k) \, T_j(x_k) = \begin{cases} 0 & \text{若 } i \ne j \\ N & \text{若 } i = j = 0 \\ \frac{N}{2} & \text{若 } i = j \ne 0 \end{cases}~ $$ 其中：$N$ 是一个整数，满足 $N > \max(i, j)$；$x_k$ 是 $T_N(x)$ 的 $N$ 个切比雪夫节点，定义为： $$ x_k = \cos\left( \pi\frac{2k + 1}{2N} \right), \quad k = 0, 1, \dots, N - 1~ $$ 对于第二类切比雪夫多项式 $U_n$，若 $N > i + j$，并采用相同的节点 $x_k$，则也存在类似的离散正交关系：

　　 带权函数 $(1 - x_k^2)$ 的情况： $$ \sum_{k = 0}^{N - 1} U_i(x_k) \, U_j(x_k) \, (1 - x_k^2) = \begin{cases} 0 & \text{若 } i \ne j \\ \frac{N}{2} & \text{若 } i = j \end{cases}~ $$ 不带权函数的情况： $$ \sum_{k = 0}^{N - 1} U_i(x_k) \, U_j(x_k) = \begin{cases} 0 & \text{若 } i \not\equiv j \pmod{2} \\ N \cdot (1 + \min\{i, j\}) & \text{若 } i \equiv j \pmod{2} \end{cases}~ $$ 这些离散正交关系在数值分析、傅里叶–切比雪夫级数展开、谱方法以及高效的数值积分（如 Clenshaw–Curtis 积分）中具有重要意义。

　　 对于任意整数 $N > i + j$，基于第二类切比雪夫多项式 $U_N(x)$ 的 $N$ 个零点： $$ y_k = \cos\left( \pi \cdot \frac{k + 1}{N + 1} \right),\quad k = 0, 1, \dots, N - 1,~ $$ 可以得到以下求和公式：

　　 带权函数 $(1 - y_k^2)$ 的情况： $$ \sum_{k = 0}^{N - 1} U_i(y_k)\, U_j(y_k)\, (1 - y_k^2) = \begin{cases} 0 & \text{若 } i \ne j \\ \frac{N + 1}{2} & \text{若 } i = j \end{cases}~ $$ 再看不带权函数的情况： $$ \sum_{k = 0}^{N - 1} U_i(y_k)\, U_j(y_k) = \begin{cases} 0 & \text{若 } i \not\equiv j \pmod{2} \\ (\min\{i, j\} + 1) (N - \max\{i, j\}) & \text{若 } i \equiv j \pmod{2} \end{cases}~ $$

最小无穷范数（∞-范数最小）

　　 对于任意给定的 $n \geq 1$，在所有次数为 $n$、首项系数为 1 的多项式（即一式多项式）中： $$ f(x) = \frac{1}{2^{n - 1}} T_n(x)~ $$ 是在区间 $[-1,1]$ 上最大绝对值最小的那一个。

　　 该多项式在区间 $[-1,1]$ 上的最大绝对值为： $$ \frac{1}{2^{n - 1}}~ $$ 并且其绝对值 $|f(x)|$ 在以下 $n + 1$ 个点上达到该最大值： $$ x = \cos\left( \frac{k\pi}{n} \right), \quad 0 \leq k \leq n~ $$

　　 证明

　　 我们设 $w_n(x)$ 是一个次数为 $n$、首项系数为 1 的多项式，且它在区间 $[-1,1]$ 上的最大绝对值小于 $1/2^{n-1}$。

　　 定义函数： $$ f_n(x) = \frac{1}{2^{n-1}} T_n(x) - w_n(x)~ $$ 由于在 $T_n$ 的极值点处有： $$ |w_n(x)| < \left| \frac{1}{2^{n-1}} T_n(x) \right|~ $$ 所以：

　　 当 $x = \cos\left(\frac{2k\pi}{n}\right)$，且 $0 \leq 2k \leq n$ 时， $$ f_n(x) > 0~ $$ 当 $x = \cos\left(\frac{(2k + 1)\pi}{n}\right)$，且 $0 \leq 2k + 1 \leq n$ 时， $$ f_n(x) < 0~ $$ 根据介值定理，函数 $f_n(x)$ 在 $[-1,1]$ 上至少有 $n$ 个零点。但这是不可能的，因为 $f_n(x)$ 是一个次数为 $n - 1$ 的多项式。根据代数学基本定理，次数为 $n - 1$ 的多项式至多只有 $n - 1$ 个实根，因此产生矛盾。因此，原假设不成立。即：在所有次数为 $n$、首项系数为 1 的多项式中， $$ f(x) = \frac{1}{2^{n-1}} T_n(x)~ $$ 确实是使其在 $[-1,1]$ 区间上最大绝对值最小的那个。证毕。

备注

　　 根据等振定理，在所有次数不超过 $n$ 的多项式中，若某个多项式 $f$ 在区间 $[-1,1]$ 上的无穷范数 $\|f\|_\infty$ 取得最小值，当且仅当存在 $n + 2$ 个点 $-1 \leq x_0 < x_1 < \cdots < x_{n+1} \leq 1$，使得：$|f(x_i)| = \|f\|_\infty$

　　 当然，区间 $[-1,1]$ 上的零多项式自身就是对自己的最佳逼近，其 $\infty$-范数也是最小的。

　　 然而，在上面的讨论中，$|f|$ 仅在 $n + 1$ 个点上达到最大值，这是因为我们寻找的是次数正好为 $n$（且 $n \geq 1$）的最佳多项式。因此，前述等振定理在此情形下并不适用。

切比雪夫多项式作为更一般多项式族的特例

　　 切比雪夫多项式是超球多项式（ultraspherical 或 Gegenbauer 多项式）$C_n^{(\lambda)}(x)$ 的特例，而超球多项式又是 Jacobi 多项式 $P_n^{(\alpha, \beta)}(x)$ 的特例：

　　 对于第一类切比雪夫多项式 $T_n(x)$： $$ \begin{aligned} T_n(x) &= \frac{n}{2} \lim_{q \to 0} \frac{1}{q} \, C_n^{(q)}(x) \quad \text{（当 } n \geq 1\text{）}\\ &= \frac{1}{\binom{n - \frac{1}{2}}{n}} P_n^{(-\frac{1}{2}, -\frac{1}{2})}(x) = \frac{2^{2n}}{\binom{2n}{n}} P_n^{(-\frac{1}{2}, -\frac{1}{2})}(x) \end{aligned}~ $$ 对于第二类切比雪夫多项式 $U_n(x)$： $$ \begin{aligned} U_n(x) &= C_n^{(1)}(x)\\ &= \frac{n+1}{\binom{n + \frac{1}{2}}{n}} P_n^{(\frac{1}{2}, \frac{1}{2})}(x) = \frac{2^{2n + 1}}{\binom{2n + 2}{n + 1}} P_n^{(\frac{1}{2}, \frac{1}{2})}(x)\\ \end{aligned}~ $$ 此外，切比雪夫多项式也是 Dickson 多项式的特例： $$ D_n(2x\alpha, \alpha^2) = 2\alpha^n T_n(x)~ $$ $$ E_n(2x\alpha, \alpha^2) = \alpha^n U_n(x)~ $$ 特别地，当 $\alpha = \frac{1}{2}$ 时，它们之间的关系为：$D_n(x, \tfrac{1}{4}) = 2^{1 - n} T_n(x)$ 和 $E_n(x, \tfrac{1}{4}) = 2^{-n} U_n(x)$

其他性质

　　 由 $y = T_n(x)$ 所描绘的曲线，或者等价地，由参数方程 $$ y = T_n(\cos \theta) = \cos\left(n\theta\right) , \quad x = \cos \theta~ $$ 所表示的曲线，是 Lissajous 曲线（李萨如曲线）的一个特例，其频率比为 $n$。

　　 类似于公式： $$ T_n(\cos \theta) = \cos\left(n\theta\right) ~ $$ 我们还有如下类似公式： $$ T_{2n+1}(\sin \theta) = (-1)^n \sin\left((2n + 1)\theta\right) ~ $$ 对于 $x \ne 0$，有： $$ T_n\left( \frac{x + x^{-1}}{2} \right) = \frac{x^n + x^{-n}}{2}~ $$ 以及： $$ x^n = T_n\left( \frac{x + x^{-1}}{2} \right) + \frac{x - x^{-1}}{2} \cdot U_{n-1}\left( \frac{x + x^{-1}}{2} \right)~ $$ 这些恒等式可由 $x = e^{i\theta}$ 情形下的定义直接推出。

　　 此外，勒让德多项式与切比雪夫多项式之间也存在如下关系： $$ \sum_{k=0}^{n} P_k(x)\, T_{n-k}(x) = (n + 1) P_n(x)~ $$ $$ \sum_{k=0}^{n} P_k(x)\, P_{n-k}(x) = U_n(x)~ $$ 这些恒等式可以通过生成函数与离散卷积方法加以证明。

切比雪夫多项式作为行列式的表示

　　 根据其递推定义，切比雪夫多项式可以表示为某些特殊三对角矩阵的行列式，矩阵大小为 $k \times k$： $$ T_k(x) = \det \begin{bmatrix} x & 1 & 0 & \cdots & 0 \\ 1 & 2x & 1 & \ddots & \vdots \\ 0 & 1 & 2x & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & 1 & 2x \end{bmatrix}~ $$ 第二类切比雪夫多项式 $U_k$ 也有类似的三对角矩阵行列式表示形式。

5. 示例

第一类

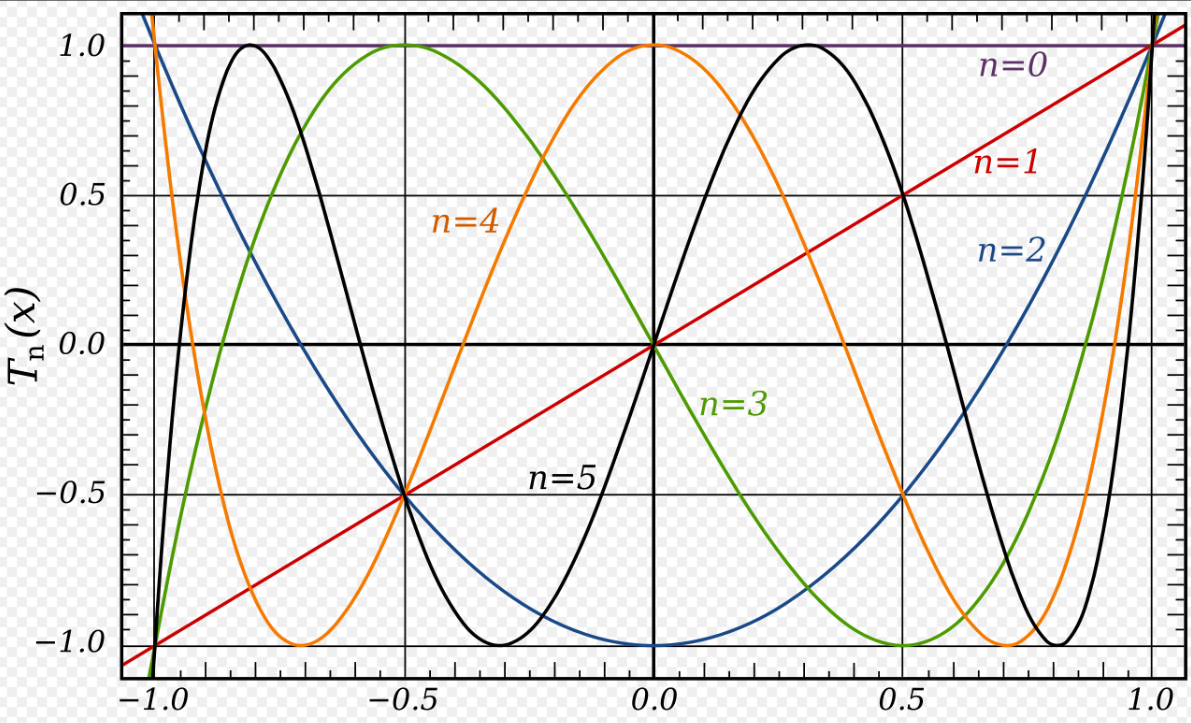
　　 前几项第一类切比雪夫多项式（参见 OEIS: A028297）为：

图
图 3：在定义域 $-1 < x < 1$ 内，前几项第一类切比雪夫多项式如下：平滑变化的 $T_0, T_1, T_2, T_3, T_4$ 和 $T_5$。

　　 $$ \begin{aligned} T_{0}(x)&=1,\\[1ex] T_{1}(x)&=x,\\[1ex] T_{2}(x)&=2x^{2}-1,\\[1ex] T_{3}(x)&=4x^{3}-3x,\\[1ex] T_{4}(x)&=8x^{4}-8x^{2}+1,\\[1ex] T_{5}(x)&=16x^{5}-20x^{3}+5x,\\[1ex] T_{6}(x)&=32x^{6}-48x^{4}+18x^{2}-1,\\[1ex] T_{7}(x)&=64x^{7}-112x^{5}+56x^{3}-7x,\\[1ex] T_{8}(x)&=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1,\\[1ex] T_{9}(x)&=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x,\\[1ex] T_{10}(x)&=512x^{10}-1280x^{8}+1120x^{6}-400x^{4}+50x^{2}-1. \end{aligned}~ $$

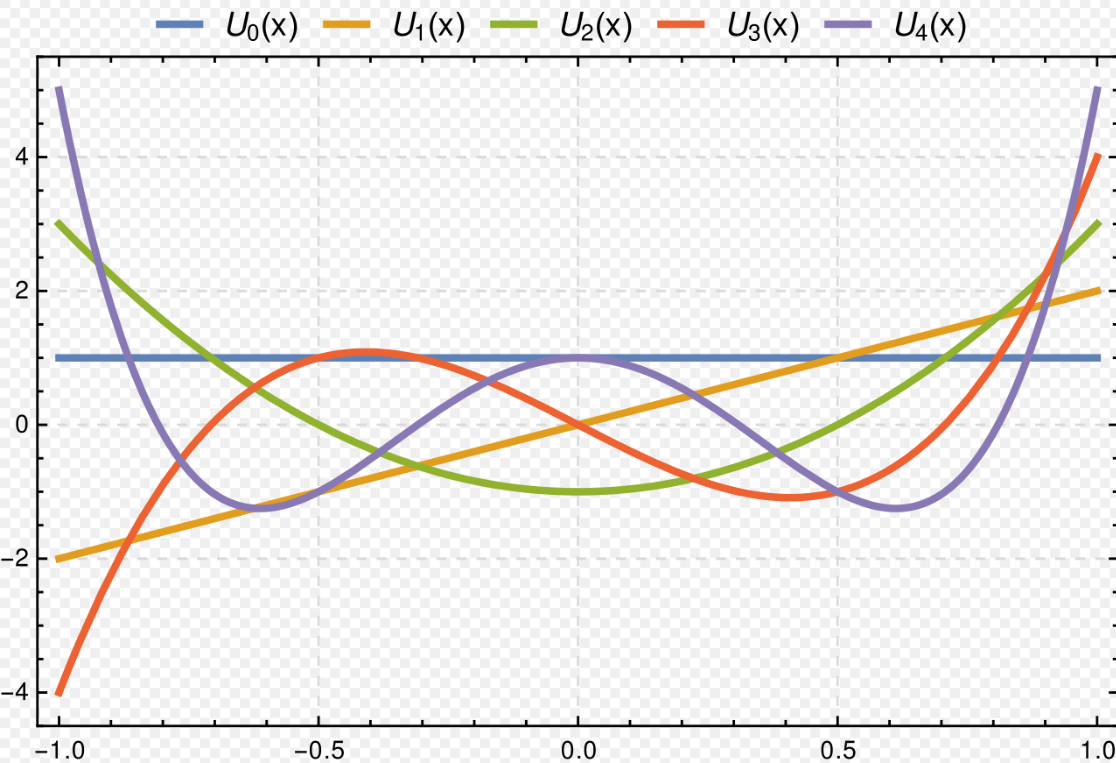
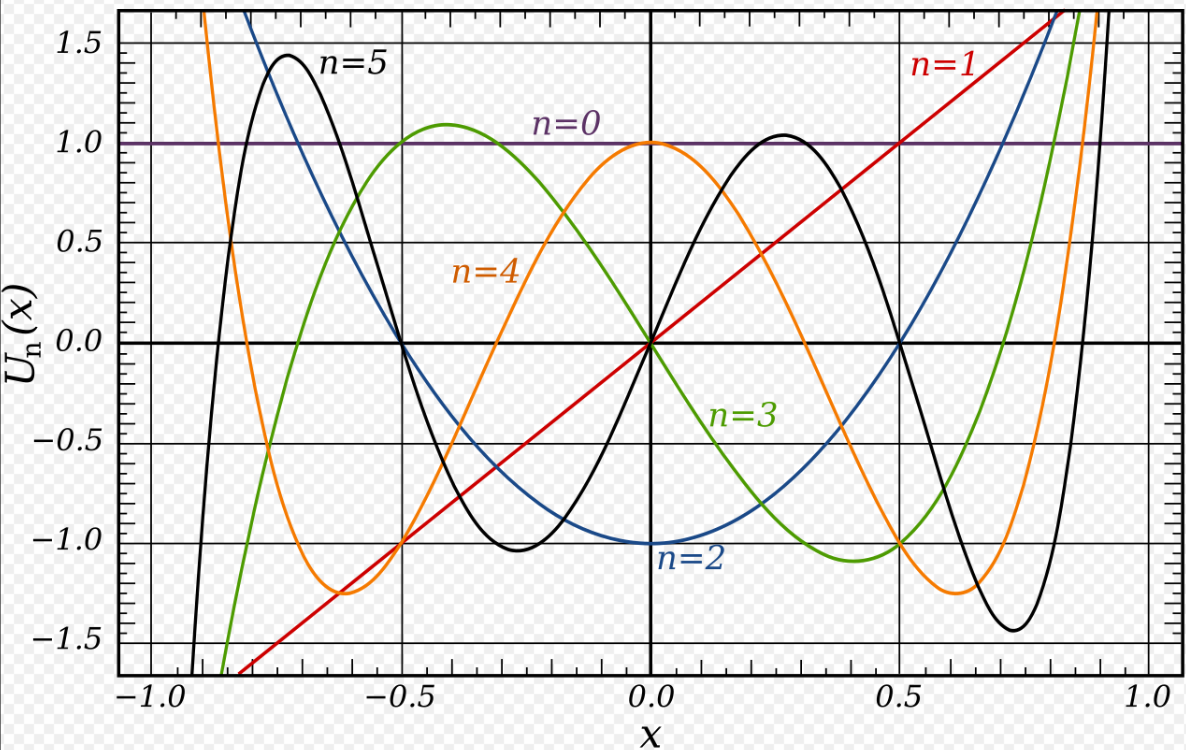
第二类（Second kind）

图
图 4：在定义域 $-1 < x < 1$ 内，前几项第二类切比雪夫多项式为：平滑变化的 $U_0, U_1, U_2, U_3, U_4$ 和 $U_5$。尽管图像中不可见，但实际上：$U_n(1) = n + 1,\quad U_n(-1) = (n + 1)(-1)^n$

　　 前几项第二类切比雪夫多项式（参见 OEIS: A053117）为： $$ \begin{aligned} U_0(x) &= 1 \\ U_1(x) &= 2x \\ U_2(x) &= 4x^2 - 1 \\ U_3(x) &= 8x^3 - 4x \\ U_4(x) &= 16x^4 - 12x^2 + 1 \\ U_5(x) &= 32x^5 - 32x^3 + 6x \\ U_6(x) &= 64x^6 - 80x^4 + 24x^2 - 1 \\ U_7(x) &= 128x^7 - 192x^5 + 80x^3 - 8x \\ U_8(x) &= 256x^8 - 448x^6 + 240x^4 - 40x^2 + 1 \\ U_9(x) &= 512x^9 - 1024x^7 + 672x^5 - 160x^3 + 10x \\ U_{10}(x) &= 1024x^{10} - 2304x^8 + 1792x^6 - 560x^4 + 60x^2 - 1 \end{aligned}~ $$

6. 作为一组基函数

图
图 5：上图为非光滑函数 $y = -x^3 H(-x)$，其中 $H$ 是 Heaviside 阶跃函数；下图为其切比雪夫展开的第 5 阶部分和。在图像分辨率下，第 7 阶部分和与原函数几乎无法区分。

　　 在适当的 Sobolev 空间中，切比雪夫多项式构成了一组正交归一基。因此，同属该空间的函数在区间 $-1 \leq x \leq 1$ 上可以表示为如下形式的展开式：\(^\text{[16]}\) $$ f(x) = \sum_{n=0}^{\infty} a_n T_n(x)~ $$ 此外，如前所述，切比雪夫多项式构成一组正交基，这意味着系数 $a_n$ 可以通过内积的方式方便地求得。这个展开式称为切比雪夫级数，或切比雪夫展开。

　　 由于切比雪夫级数可以通过变量变换与傅里叶余弦级数建立对应关系，因此适用于傅里叶级数的所有定理、恒等式等，也都有相应的切比雪夫形式。\(^\text{[16]}\) 这些性质包括：

　　 Chebfun 软件包支持基于切比雪夫展开的函数操作，是这类方法在实际计算中的一个重要实现工具。

示例 1

　　 考虑对函数 $ \log\left(1 + x\right) $ 进行切比雪夫展开。我们可以将其表示为： $$ \log\left(1 + x\right) = \sum_{n=0}^{\infty} a_n T_n(x)~ $$ 系数 $a_n$ 可以通过内积计算，或者使用离散正交性条件求得。对于内积，有如下公式： $$ \int_{-1}^{+1} \frac{T_m(x)\, \log\left(1+x\right) }{\sqrt{1 - x^2}}\, dx = \sum_{n=0}^{\infty} a_n \int_{-1}^{+1} \frac{T_m(x) T_n(x)}{\sqrt{1 - x^2}}\, dx~ $$ 由此可以推得： $$ a_n = \begin{cases} - \log 2, & \text{当 } n = 0 \\ \displaystyle \frac{-2 (-1)^n}{n}, & \text{当 } n > 0 \end{cases}~ $$ 当无法解析地计算内积时，可使用离散正交性条件来近似求得系数： $$ a_n \approx \frac{2 - \delta_{0n}}{N} \sum_{k=0}^{N-1} T_n(x_k)\, \log\left(1 + x_k\right) ~ $$ 其中：$\delta_{ij}$ 是克罗内克 δ 函数；$x_k$ 是 $T_N(x)$ 的 N 个 Gauss–Chebyshev 零点，即： $$ x_k = \cos\left( \frac{\pi(k + \tfrac{1}{2})}{N} \right)~ $$ 对于任意 $N$，这些近似系数在节点 $x_k$ 处给出函数的精确逼近，在节点之间的误差是可控的。当 $N \to \infty$ 时，获得的是函数在区间 $[-1,1]$ 上的精确展开。 收敛速度取决于函数的性质及其光滑性。

　　 此外，这还允许我们通过离散余弦变换非常高效地计算近似系数 $a_n$： $$ a_n \approx \frac{2 - \delta_{0n}}{N} \sum_{k=0}^{N-1} \cos\left( \frac{n\pi(k + \tfrac{1}{2})}{N} \right) \log\left(1 + x_k\right) ~ $$

示例 2

　　 再看一个例子： $$ \begin{aligned} (1 - x^2)^{\alpha} &= -\frac{1}{\sqrt{\pi}}\,\frac{\Gamma\left(\tfrac{1}{2} + \alpha\right)}{\Gamma(\alpha + 1)} + 2^{1 - 2\alpha} \sum_{n=0}^{\infty} (-1)^n \binom{2\alpha}{\alpha - n} T_{2n}(x)\\ &= 2^{-2\alpha} \sum_{n=0}^{\infty} (-1)^n \binom{2\alpha + 1}{\alpha - n} U_{2n}(x) \end{aligned}~ $$

部分和

　　 函数： $$ f(x) = \sum_{n=0}^{\infty} a_n T_n(x)~ $$ 的部分和在函数逼近与微分方程求解中非常有用（参见谱方法）。确定系数 $a_n$ 的两种常见方法是：使用内积法，如 Galerkin 方法；使用配点法，它与插值密切相关。

　　 作为插值形式，$N$ 项部分和的 $N$ 个系数通常是在切比雪夫–高斯–洛巴托点（Chebyshev–Gauss–Lobatto 点，又称 Lobatto 网格）上获得的。这种取点方式可以最小化误差，并避免在均匀网格中常见的龙格现象。这些节点由所用最高阶切比雪夫多项式的极值点加上区间端点构成，表达式为： $$ x_k = -\cos\left( \frac{k\pi}{N - 1} \right),\quad k = 0, 1, \dots, N - 1~ $$

切比雪夫形式的多项式

　　 任意一个次数为 $N$ 的多项式都可以用第一类切比雪夫多项式表示出来。\(^\text{[10]}\) 这样的多项式 $p(x)$ 具有如下形式： $$ p(x) = \sum_{n=0}^{N} a_n T_n(x)~ $$ 以切比雪夫形式表示的多项式可以通过 Clenshaw 算法进行高效计算。

7. 与切比雪夫多项式相关的多项式族

　　 有时会使用一些与切比雪夫多项式密切相关的多项式，记作 $C_n(x)$ 和 $S_n(x)$。它们的定义如下：\(^\text{[18]}\) $$ C_n(x) = 2T_n\left(\frac{x}{2}\right), \qquad S_n(x) = U_n\left(\frac{x}{2}\right)~ $$ 它们满足以下关系式： $$ C_n(x) = S_n(x) - S_{n-2}(x)~ $$ A. F. Horadam 将多项式 $C_n(x)$ 称为 Vieta–Lucas 多项式，记作 $v_n(x)$，将多项式 $S_n(x)$ 称为 Vieta–Fibonacci 多项式，记作 $V_n(x)$。\(^\text{[19]}\) 这两类多项式的列表可以在维耶特的《数学著作集》第九章第六和第七定理中找到。\(^\text{[20]}\) 实变量下的 Vieta–Lucas 多项式和 Vieta–Fibonacci 多项式（后者在指标上略有平移，并涉及 $i$ 的幂）分别等价于虚数变量下的 Lucas 多项式 $L_n$ 和 Fibonacci 多项式 $F_n$。

　　 平移切比雪夫多项式第一类和平移第二类切比雪夫多项式与标准切比雪夫多项式之间的关系如下：\(^\text{[18]}\) $$ T_n^*(x) = T_n(2x - 1),\qquad U_n^*(x) = U_n(2x - 1)~ $$ 当切比雪夫多项式的自变量满足 $2x - 1 \in [-1, 1]$ 时，平移后的自变量满足 $x \in [0, 1]$。类似地，也可以为任意区间 $[a, b]$ 定义平移的切比雪夫多项式。

　　 大约在 1990 年，术语 “第三类” 和 “第四类” 切比雪夫多项式开始使用，尽管这些多项式在此之前已经以 “翼型多项式” 的名称被研究。根据 J. C. Mason 和 G. H. Elliott 的说法，这些术语由 Walter Gautschi 在与正交多项式领域的同事讨论后提出。\(^\text{[21]}\) 第三类切比雪夫多项式定义为： $$ V_n(x) = \frac{\cos\left(\left(n + \tfrac{1}{2}\right)\theta\right)}{\cos\left(\tfrac{\theta}{2}\right)} = \sqrt{\frac{2}{1 + x}}\, T_{2n+1}\left(\sqrt{\frac{x + 1}{2}}\right)~ $$ 第四类切比雪夫多项式定义为： $$ W_n(x) = \frac{\sin\left(\left(n + \tfrac{1}{2}\right)\theta\right)}{\sin\left(\tfrac{\theta}{2}\right)} = U_{2n}\left(\sqrt{\frac{x + 1}{2}}\right)~ $$ 其中 $\theta = \arccos x$。\(^\text{[21][22]}\) 它们与狄利克雷核是一致的。

　　 在翼型文献中，$V_n(x)$ 和 $W_n(x)$ 分别被记作 $t_n(x)$ 和 $u_n(x)$。

　　 多项式族 $T_n(x)$、$U_n(x)$、$V_n(x)$ 和 $W_n(x)$ 在以下权重函数下是正交的： $$ (1 - x^2)^{-1/2}, \quad (1 - x^2)^{1/2}, \quad (1 - x)^{-1/2}(1 + x)^{1/2}, \quad (1 + x)^{-1/2}(1 - x)^{1/2}~ $$ 它们分别与下列参数的雅可比多项式 $P_n^{(\alpha,\beta)}(x)$ 成正比：\(^\text{[22]}\)

　　 $(\alpha, \beta) = \left(-\tfrac{1}{2}, -\tfrac{1}{2} \right)$, $(\alpha, \beta) = \left( \tfrac{1}{2}, \tfrac{1}{2} \right)$, $(\alpha, \beta) = \left( -\tfrac{1}{2}, \tfrac{1}{2} \right)$, $(\alpha, \beta) = \left( \tfrac{1}{2}, -\tfrac{1}{2} \right)$

　　 这四类多项式族都满足以下递推关系：$p_n(x) = 2x\,p_{n-1}(x) - p_{n-2}(x)$ 其中 $p_0(x) = 1$ 其中 $p_n$ 可以是 $T_n$、$U_n$、$V_n$ 或 $W_n$，但它们的不同在于 $p_1(x)$ 的初始值分别是：$x$，$2x$，$2x - 1$，$2x + 1$\(^\text{[21]}\)

偶数阶修正切比雪夫多项式

　　 某些应用依赖于切比雪夫多项式，但又无法接受其在零点没有根的特性，这使得标准切比雪夫多项式无法用于这类应用。例如，使用等端接无源网络的偶数阶切比雪夫滤波器设计就是一个典型案例 \(^\text{[23]}\)。不过，我们可以通过修改偶数阶切比雪夫多项式，使其最低的根移动到零点，同时仍保持切比雪夫多项式特有的等波纹（equi-ripple）特性。这样修改后的多项式包含两个在零点的根，通常称为偶数阶修正切比雪夫多项式。

　　 偶数阶修正切比雪夫多项式可以使用类似于标准切比雪夫多项式的构造方法，只是使用了修正后的切比雪夫节点。

　　 定义如下： $$ P_N = \prod_{i=1}^N (x - C_i)~ $$ 其中：

　　 而偶数阶修正切比雪夫多项式的构造方式为： $$ Pe_N = \prod_{i=1}^N (x - Ce_i)~ $$ 其中：

　　 例如，上述例子中的 4 阶标准切比雪夫多项式为：$X^4 - X^2 + 0.125$ 通过观察可知，该多项式在零点没有根。而如果使用偶数阶修正切比雪夫节点构造所得的 4 阶偶数阶修正切比雪夫多项式为：$X^4 - 0.828427X^2$ 可以看到，该多项式包含两个在零点的根，因此可以用于那些需要在零点有根的应用场景中。

8. 参见

9. 参考文献

  1. Rivlin, Theodore J. (1974). 《第 2 章，极值性质》，《切比雪夫多项式》，纯粹与应用数学系列（第一版），纽约-伦敦-悉尼：Wiley-Interscience（John Wiley & Sons），第 56–123 页。ISBN 978-047172470-4。
  2. Lanczos, C. (1952). “通过最小迭代法求解线性方程组”。《美国国家标准局研究期刊》，49(1): 33。doi:10.6028/jres.049.006。
  3. 切比雪夫最早于 1853 年在圣彼得堡科学院宣读论文中提出以其命名的多项式：
    Chebyshev, P. L. (1854). “被称为平行四边形的机构理论”。《圣彼得堡科学院外国学者文集》（法语）7: 539–586。
    另见独立出版版：Chebyshev, P. L. (1853). 《被称为平行四边形的机构理论》，圣彼得堡：帝国科学院印刷所。doi:10.3931/E-RARA-120037。
  4. Schaeffer, A. C. (1941). “A. Markoff 和 S. Bernstein 关于多项式及相关函数的不等式”。《美国数学会通报》47(8): 565–579。doi:10.1090/S0002-9904-1941-07510-5。
  5. Ritt, J. F. (1922). “素多项式与合成多项式”。《美国数学会会刊》23: 51–66。doi:10.1090/S0002-9947-1922-1501189-9。
  6. Demeyer, Jeroen (2007).《多项式环上的丢番图集合与函数域上的希尔伯特第十问题》（PDF，博士论文），第 70 页。2007 年 7 月 2 日存档。
  7. Bateman & Bateman Manuscript Project 1953，第 184 页，等式 3–4。
  8. Beckenbach, E. F.; Seidel, W.; Szász, Otto (1951). “勒让德和超球面多项式的递归行列式”，《杜克数学杂志》，18: 1–10。doi:10.1215/S0012-7094-51-01801-7。
  9. Bateman & Bateman Manuscript Project 1953，第 187 页，等式 47–48。
  10. Mason & Handscomb 2002。
  11. Cody, W. J. (1970). “关于函数的实用有理与多项式逼近的综述”，《SIAM 评论》，12(3): 400–423。doi:10.1137/1012082。
  12. Mathar, Richard J. (2006). “逆多项式的切比雪夫级数展开”。《计算与应用数学杂志》，196(2): 596–607。arXiv\:math/0403344。doi:10.1016/j.cam.2005.10.013。
  13. Gürtaş, Y. Z. (2017). “切比雪夫多项式与 cos(2π/n) 的最小多项式”，《美国数学月刊》，124(1): 74–78。doi:10.4169/amer.math.monthly.124.1.74。
  14. Wolfram, D. A. (2022). “将第一类与第二类切比雪夫多项式因式分解为 cos(2π/d) 的最小多项式”。《美国数学月刊》，129(2): 172–176。doi:10.1080/00029890.2022.2005391。
  15. Rayes, M. O.; Trevisan, V.; Wang, P. S. (2005). “切比雪夫多项式的因式分解性质”，《计算与数学应用》50(8–9): 1231–1240。doi:10.1016/j.camwa.2005.07.003。
  16. Boyd, John P. (2001). 《切比雪夫与傅里叶谱方法》（PDF，第二版），Dover 出版社。ISBN 0-486-41183-4。2010 年 3 月 31 日存档。2009 年 3 月 19 日访问。
  17. “切比雪夫插值：一个交互式导览”。2017 年 3 月 18 日存档。2016 年 6 月 2 日访问。
  18. Hochstrasser 1972，第 778 页。
  19. Horadam, A. F. (2002). “Viète 多项式”（PDF），《斐波那契季刊》，40(3): 223–232。
  20. Viète, François (1646). 《弗朗西斯·维耶特数学全集》，由 Francisci a Schooten 整理（PDF），法国国家图书馆藏。
  21. Mason, J. C.; Elliott, G. H. (1993). “通过四类切比雪夫多项式展开实现的近极小复数逼近”，《计算与应用数学杂志》，46(1–2): 291–300。doi:10.1016/0377-0427(93)90303-S。
  22. Desmarais, Robert N.; Bland, Samuel R. (1995). “翼型多项式性质表”，《NASA 参考出版物 1343》，美国国家航空航天局。
  23. Saal, Rudolf (1979 年 1 月). 《滤波器设计手册》（英德文对照，第一版），德国慕尼黑：通用电气公司出版社，第 25, 26, 56–61, 116, 117 页。ISBN 3-87087-070-2。

10. 进一步阅读

11. 外部链接

                     

© 保留一切权利