2010 年考研数学试题(数学一)
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 选择题
- 极限 $\displaystyle \lim_{n\to\infty}[\frac{x^2}{(x-a)+(x+b)}]^x$=$(\quad )$
(A) $1$
(B) $e$
(C) $e^{a-b}$
(D) $e^{b-a}$ - 设函数 $z=z(x,y)$ 由方程 $\displaystyle F(\frac{y}{x},\frac{z}{x}=0)$ 确定,其中 $F$ 为可微函数,且 $F'_2 \neq0$,则 $\displaystyle x \frac{\partial z}{\partial x} +y \frac{\partial z}{\partial y} $=$(\quad )$
(A) $x$
(B) $z$
(C) $-x$
(D) $-z$ - 设 $m,n$ 均是正整数,则反常积分 $\displaystyle \int_0^1 \frac{\sqrt[m]{\ln^2(1-x)}}{\sqrt[n]{x}} \,\mathrm{d}{x} $ 的收敛性 $(\quad )$
(A) 仅与 $m$ 的取值有关
(B) 仅与 $n$ 的取值有关
(C) 与 $m,n$ 的取值都有关
(D) 与 $m,n$ 的取值都无关 - $\displaystyle \lim_{n\to\infty} \sum_{i=1}^n \sum_{j=1}^n \frac{n}{(n+i)(n^2+j^2)}$= $(\quad )$
(A) $\displaystyle \int_{0}^{1} \,\mathrm{d}{x} \int_{0}^{x} \frac{1}{(1+x)(1+y^2)} \,\mathrm{d}{y} $
(B)$\displaystyle \int_{0}^{1} \,\mathrm{d}{x} \int_{0}^{x} \frac{1}{(1+x)(1+y)} \,\mathrm{d}{y} $
(C)$\displaystyle \int_{0}^{1} \,\mathrm{d}{x} \int_{0}^{1} \frac{1}{(1+x)(1+y)} \,\mathrm{d}{y} $
(D)$\displaystyle \int_{0}^{1} \,\mathrm{d}{x} \int_{0}^{1} \frac{1}{(1+x)(1+y^2)} \,\mathrm{d}{y} $ - 设 $ \boldsymbol{\mathbf{A}} $ 为 $m$x$n$ 矩阵,$ \boldsymbol{\mathbf{B}} $ 为 $n$x$m$ 矩阵,$ \boldsymbol{\mathbf{E}} $ 为 $m$ 阶单位矩阵,若 $ \boldsymbol{\mathbf{AB=E}} $,则 $(\quad )$
(A) 秩 $r( \boldsymbol{\mathbf{A}} )=m$,秩 $r( \boldsymbol{\mathbf{B}} )=m$
(B) 秩 $r( \boldsymbol{\mathbf{A}} )=m$,秩 $r( \boldsymbol{\mathbf{B}} )=n$
(C) 秩 $r( \boldsymbol{\mathbf{A}} )=n$,秩 $r( \boldsymbol{\mathbf{B}} )=m$
(D) 秩 $r( \boldsymbol{\mathbf{A}} )=n$,秩 $r( \boldsymbol{\mathbf{B}} )=n$
- 设 $ \boldsymbol{\mathbf{A}} $ 为 4 阶实对称矩阵,且 $ \boldsymbol{\mathbf{A^2+A=O}} $ 。若 $ \boldsymbol{\mathbf{A}} $ 的秩为 3,则 $ \boldsymbol{\mathbf{A}} $ 相似于 $(\quad )$
(A) $ \begin{pmatrix}1& & & \\ &1& & &\\ & &1&\\& & &1\end{pmatrix} $
(B) $ \begin{pmatrix}1& & & \\ &1& & &\\ & &-1&\\& & &0\end{pmatrix} $
(C) $ \begin{pmatrix}1& & & \\ &-1& & &\\ & &-1&\\& & &0\end{pmatrix} $
(D) $ \begin{pmatrix}-1& & & \\ &-1& & &\\ & &-1& \\& & &0\end{pmatrix} $ - 设随机变量 $X$ 的分布函数 $F(x)= \left\{\begin{aligned} &0,& x<0,\\ &\frac{1}{2},& 0\le x<1\\ &1-e^{-x},& x \ge 1 \end{aligned}\right. $ ,则 $P\{X=1\}$=$(\quad )$
(A) $0$
(B) $\frac{1}{2}$
(C) $\frac{1}{2}-e^{-1}$
(D) $1-e^{-1}$ - 设 $f_1(x)$ 为标准正态分布的概率密度,$f_2(x)$ 为 $[-1,3]$ 上均匀分布的概率密度,若 $f(x)= \left\{\begin{aligned} af_1(x),\quad x\le0\\bf_2(x),\quad x>0 \end{aligned}\right. \quad $ $(a>0,b>0)$ 为概率密度,则 $a,b$ 应满足 $(\quad )$
(A) $2a+3b=4$
(B) $3a+2b=4$
(C) $a+b=1$
(D) $a+b=2$
2. 填空题
- 设 $ \left\{\begin{aligned} & x=e^{-t}\\& y=\int_0^1 \ln\left(1+u^2\right) \,\mathrm{d}{u} \end{aligned}\right. $ ,则 $\displaystyle \left. \frac{\mathrm{d}^{2}{y}}{\mathrm{d}{x}^{2}} \right\rvert _{t=0}$=$(\quad )$
- $\displaystyle \int_0^{\pi^2}\sqrt{x}\cos \sqrt{x} \,\mathrm{d}{x} $=$(\quad )$
- 已知曲线 $L$ 的方程为 $y=1- \left\lvert x \right\rvert \quad (x \in [-1,1])$,起点是 $(-1,0)$,终点为 $(1,0)$,则曲线积分 $\displaystyle \int_L xy \,\mathrm{d}{x} +x^2 \,\mathrm{d}{y} $=$(\quad )$
- 设 $\Omega=\{(x,y,z)|x^2+y^2\le z \le1\}$,则 $\Omega$ 的形心的竖坐标 $\bar z$= $(\quad )$
- 设 $\alpha_1=(1,2,-1,0) ^{\mathrm{T}} ,\alpha_2=(1,1,0,2) ^{\mathrm{T}} ,\alpha_3=(2,1,1,a) ^{\mathrm{T}} $ 。若由 $\alpha_1,\alpha_2,\alpha_3$ 生成的向量空间的维数为 2,则 $a$=$(\quad )$
- 设随机变量 $X$ 的概率分布为 $P\{X=k\}=\frac{C}{K!},k=0,1,2\dots$,则 $E(X^2)$=$(\quad )$
3. 解答题
- 求微分方程 $y''-3y'+2y=2xe^x$ 的通解。
- 求函数 $\displaystyle f(x)=\int_{1}^{x^2}(x^2-t)e^{-t^2} \,\mathrm{d}{t} $ 的单调区间与极值。
- (1) 比较 $\displaystyle \int_0^1 \left\lvert \ln t \right\rvert [ \ln\left(1+t\right) ]^n \,\mathrm{d}{t} $ 与 $\displaystyle \int_0^1 t^n \left\lvert \ln t \right\rvert \,\mathrm{d}{t} (n=1,2,\dots)$ 的大小,说明理由;
(2)记 $\displaystyle u_n= \int_0^1 \left\lvert \ln t \right\rvert [ \ln\left(1+t\right) ]^n \,\mathrm{d}{t} (n=1,2,\dots)$,求极限 $\displaystyle \lim_{n\to\infty} u_n$。 - 求幂级数 $\displaystyle \sum_{n=1}^\infty \frac{(-1)^{n-1}}{2n-1}x^{2n}$ 的收敛域及和函数。
- 设 $P$ 为椭球面 $S$:$x^2+y^2+z^2-yz=1$ 上的动点,若 $S$ 在点 $ P$ 处的切平面与 $xOy$ 面垂直,求点 $P$ 的轨迹 $C$,并计算曲面积分 $\displaystyle I=\iint_\Sigma \frac{(x+\sqrt{3}) \left\lvert y-2z \right\rvert }{\sqrt{4+y^2+z^2-4yz}} \,\mathrm{d}{S} $ ,其中 $\Sigma$ 是椭球面 $S$ 位于曲线 $ C$ 上方的部分。
- 设 $ \boldsymbol{\mathbf{A}} = \begin{pmatrix}\lambda &1&1\\0&\lambda-1&0\\1&1&\lambda\end{pmatrix} , \boldsymbol{\mathbf{b}} = \begin{pmatrix}a\\1\\1\end{pmatrix} $ 。已知线性方程组 $ \boldsymbol{\mathbf{Ax=b}} $ 存在 2 个不同的解。
(1)求 $\lambda,a$;
(2)求方程组 $ \boldsymbol{\mathbf{Ax=b}} $ 的通解。 - 已知二次型 $f(x_1,x_2,x_3)= \boldsymbol{\mathbf{x ^{\mathrm{T}} Ax}} $ 在正交变换 $ \boldsymbol{\mathbf{x=Qy}} $ 下的标准型为 $y_1^2+y_2^2$ ,且 $Q$ 的第三列为 $\displaystyle (\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2}) ^{\mathrm{T}} $。
(1)求矩阵 $ \boldsymbol{\mathbf{A}} $;
(2)证明 $ \boldsymbol{\mathbf{A+E}} $ 为正定矩阵,其中 $ \boldsymbol{\mathbf{E}} $ 为 3 阶单位矩阵。 - 设二维随机变量 $(X,Y)$ 的概率密度为 $\displaystyle f(x,y)=Ae^{-2x^2+2xy-y^2},-\infty< x<+\infty,-\infty< y<+\infty$,求常数 $A$ 及条件概率密度 $f_{Y|X}(y|x)$
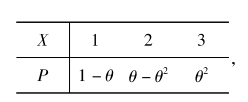
- 设总体 $X$ 的概率分布为
图 1其中参数 $\theta \in (0,1)$ 未知,以 $N_i$ 表示来自总体 $X $ 的简单随机样本(样本容量为 $n$)中等于 $i$ 的个数 $(i=1,2,3)$ ,试求常数 $a_1,a_2,a_3$ ,使 $\displaystyle T=\sum_{n=1}^3 a_iN_i$ 为 $\theta$ 的无偏估计量,并求 $T$ 的方差。