前缀和

贡献者：有机物

　　前缀和算法分为一维和二维，一维前缀和可以很快速的求序列中某一段的和。而二维前缀和可以快速求一个矩阵中某个子矩阵的和（以下讲的是以 $x_1, y_1$ 为左上角，$x_2, y_2$ 为右下角的子矩阵）。

1. 一维前缀和

　　一维前缀和的朴素做法是一个 for 循环求和，时间复杂度为：$\mathcal{O}(n \times m)$。$m$ 为询问次数。

　　而前缀和的时间复杂度为：预处理 $\mathcal{O}(n)$，查询 $\mathcal{O}(m)$。

　　一维前缀和：

\begin{equation} \sum^{r}_{i=l}a_i~, \end{equation}

　　预处理：

\begin{equation} S_i=\sum^{i}_{k=1}a_k~. \end{equation}

　　如何预处理？

\begin{equation} \because \sum^{i}_{k=1}a_k-\sum^{i-1}_{k=1}a_{k}=a_k \\ \therefore \sum^{i}_{k=1}a_k=\sum^{i-1}_{k=1}a_{k}+a_k ~,\\ \end{equation}

　　即：

\begin{equation} \\S_k-S_{k-1}=a_k\\ \\S_k=S_{k-1}+a_k~.\\ \end{equation}

　　如何求答案？

\begin{equation} \sum^{r}_{i=l}a_i=\sum^{r}_{i=1}a_i-\sum^{l-1}_{i=1}a_i=S_r-S_{l-1}~. \end{equation}

　　还有要注意的是 $S_0 = 0$，因为如果想求 $1 \sim n$ 一段数的和可以直接输出 $S_{10} - S_0 = S_{10} $。因此可以从下标为 $1$ 开始存数，这样就不需要做复杂的处理。

　　 朴素代码

const int N = 100010;
int a[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    
    while (m -- )
    {
        int l, r;
        cin >> l >> r;
        
        int res = 0;
        for (int i = l; i <= r; i ++ ) res += a[i];
        cout << res << endl;
    }
    
    return 0;
}

　　 前缀和

const int N = 100010;
int n, m, a[N], s[N];

int main() 
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
    
    while (m -- )
    {
        int l, r;
        cin >> l >> r;
        cout << s[r] - s[l - 1] << endl;    // 前缀和公式，O(1)
    }
    
    return 0;
}

2. 二维前缀和

　　二维前缀和的朴素做法是两重循环暴力求和。时间复杂度为：$\mathcal{O}(q \times nm)$。$q$ 为询问次数，$n$、$m$ 为矩阵大小。

　　而二维前缀和的时间复杂度为 $\mathcal{O}(n \times m)$

　　二维前缀和：

\begin{equation} \sum^{x2}_{i = x1}\sum^{y2}_{j = y1} a_{ij}~, \end{equation}

　　预处理：

\begin{equation} S_{ij} = \sum^{i}_{k_1 = 1} \sum^{j}_{k_2 = 1} a_{k_1 k_2}~. \end{equation}

　　如何预处理？

　　在预处理 $S_{ij}$ 时，要注意 $S_{i - 1, m}$ 和 $S_{i, j - 1}$ 都已经被算过了，因为预处理是逐行逐列来计算的（重复地方不重复计算）。

\begin{equation} S_{ij} = \sum^{i}_{k_1 = 1} \sum^{j}_{k_2 = 1} a_{k_1 k_2} = \sum^{i - 1}_{k_1 = 1} \sum^{j}_{k_2 = 1} + \sum^{i}_{k_1 = 1} \sum^{j - 1}_{k_2 = 1} - \sum^{i- 1}_{k_1 = 1} \sum^{j - 1}_{k_2 = 1} + a_{i, j}~, \end{equation}

　　即：

\begin{equation} S_{i, j} = S_{i - 1, j} + S_{i, j - 1} - S_{i - 1, j - 1} + a_{i, j}~. \end{equation}

　　如何求答案？

\begin{equation} \sum^{x_2}_{i = x_1}\sum^{y_2}_{j = y_1} a_{ij} = \sum^{x_2}_{k_1 = 1} \sum^{y_2}_{k_2 = 1} a_{k_1 k_2} - \sum^{x_1 - 1}_{k_1 = 1} \sum^{y_2}_{k_2 = 1} a_{k_1 k_2} - \sum^{x_2}_{k_1 = 1} \sum^{y_1 - 1}_{k_2 = 1} a_{k_1 k_2} + \sum^{x_1 - 1}_{k_1 = 1} \sum^{y_1 - 1}_{k_2 = 1} a_{k_1 k_2}~, \end{equation}

　　即：

\begin{equation} S_{x_2, y_2} - S_{x_1 - 1, y_2} - S_{x_2, y_1 - 1} + S_{x_1 - 1, y_1 - 1}~. \end{equation}

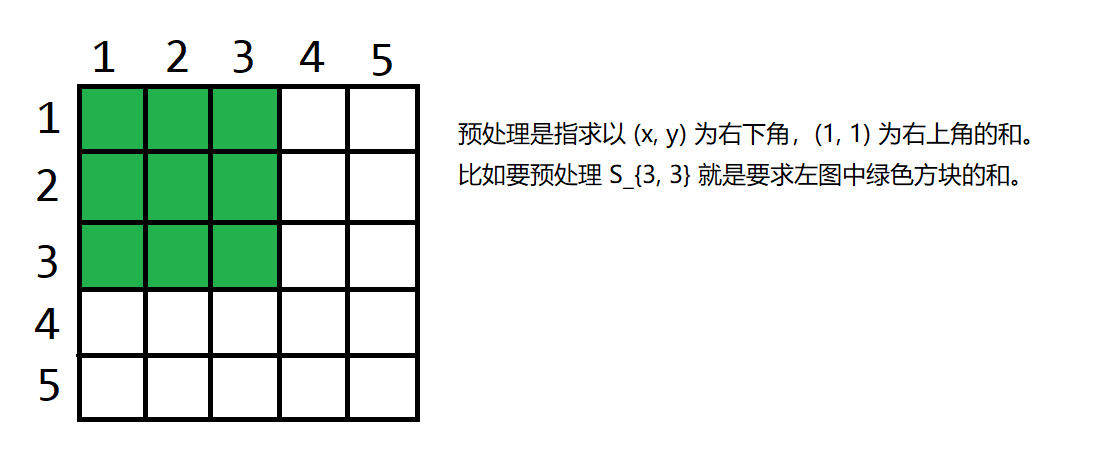
　　二维前缀和可能有点抽象，可以根据几张图片来对二维前缀和有个更好的理解。

图 1：预处理 $1$

图 2：预处理 $2$

图 3：预处理 $3$

图 4：预处理 $4$

图 5：预处理 $5$

图 6：预处理 $6$

　　求前缀和的公式类似推导预处理的过程。

　　 朴素代码

const int N = 1010;
int n, m, q, a[N][N], s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);
    
    while (q -- ) 
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        
        int res = 0;
        for (int i = x1; i <= x2; i ++ )
            for (int j = y1; j <= y2; j ++ )
                res += a[i][j];
        
        cout << res << endl;
    }
    
    return 0;
}

　　二维前缀和代码：

const int N = 1010;
int n, m, q, a[N][N], s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            scanf("%d", &a[i][j]);
            s[i][j] = s[i - 1][j] + s[i][j - 1] 
            - s[i - 1][j - 1] + a[i][j];    // 预处理公式
        }
        
    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", 
        s[x2][y2] - s[x1 - 1][y2] 
        - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);  // 前缀和公式
    }
    
    return 0;
}