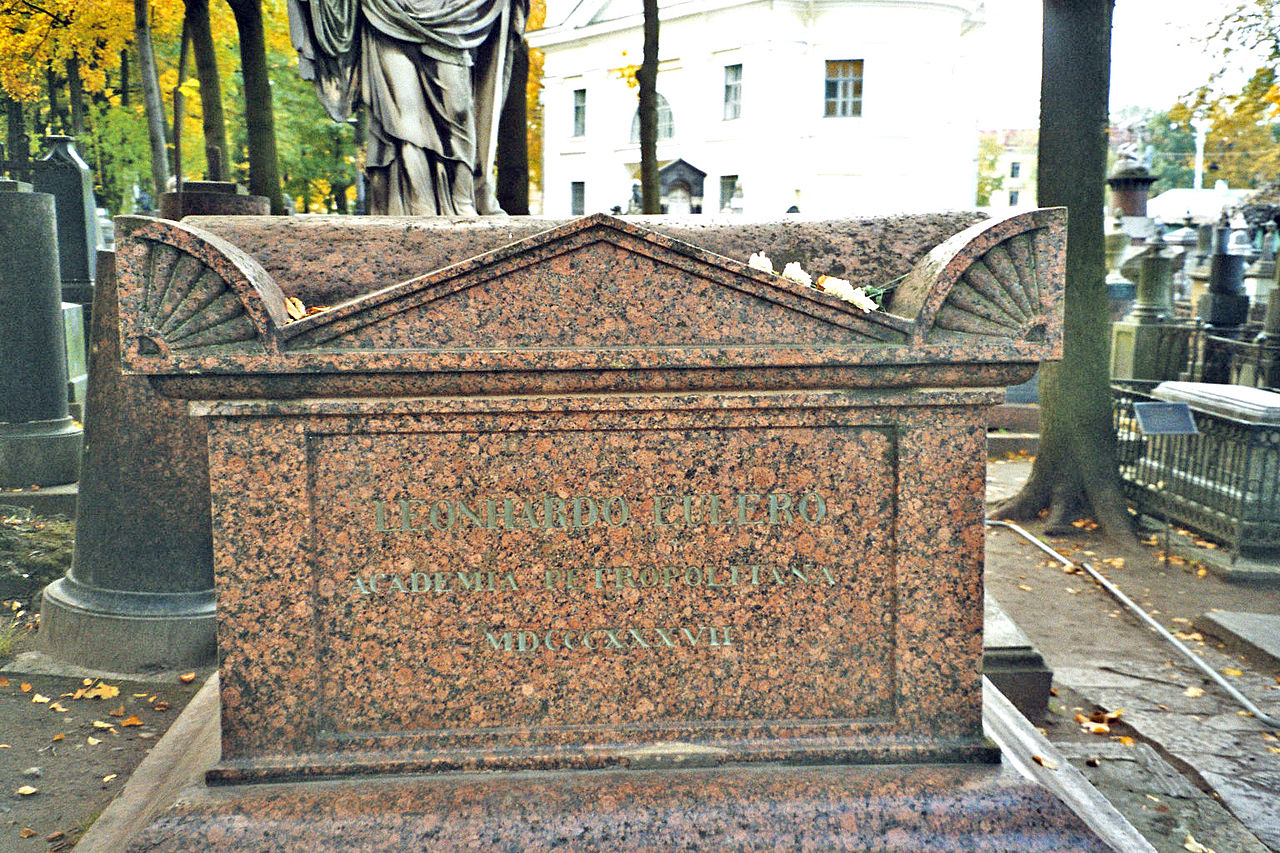莱昂哈德·欧拉（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 莱昂哈德·欧拉（Leonhard Euler，发音：/ˈɔɪlər/ OY-lər；[b] 德语：[ˈleːɔnhaʁt ˈʔɔʏlɐ] ⓘ，瑞士标准德语：[ˈleɔnhard ˈɔʏlər]；1707 年 4 月 15 日 – 1783 年 9 月 18 日）是瑞士数学家、物理学家、天文学家、地理学家、逻辑学家和工程师。他是图论和拓扑学的创始人，并在其他多个数学分支（如解析数论、复分析和微积分）中做出了开创性和深远的发现。他引入了许多现代数学术语和符号，包括数学函数的概念。他还以在力学、流体动力学、光学、天文学和音乐理论等领域的贡献而闻名。

　　 欧拉被认为是历史上最伟大、最多产的数学家之一，也是 18 世纪最伟大的数学家。许多在欧拉去世后才产生的伟大数学家都承认他在这一领域的重要性，正如他们的名言所示：皮埃尔-西蒙·拉普拉斯曾通过一句话表达欧拉对数学的影响：“读欧拉，读欧拉，他是我们的导师。” 卡尔·弗里德里希·高斯写道：“研究欧拉的作品将是学习数学各个领域的最佳学校，其他任何东西都无法替代它。” 欧拉的 866 篇论文和他的信件正在被收集成《欧拉全集》（Opera Omnia Leonhard Euler），完成后将包含 81 卷四开本。欧拉大部分成年生活都在俄罗斯圣彼得堡和普鲁士首都柏林度过。

　　 欧拉还被认为是第一个推广使用希腊字母π（小写 pi）来表示圆的周长与直径的比率的人，以及第一个使用符号 f(x)来表示函数值的人。他还使用字母 i 表示虚数单位√(-1)，使用希腊字母Σ（大写 sigma）表示求和，使用希腊字母Δ（大写 delta）表示有限差分，使用小写字母表示三角形的边，使用大写字母表示角度。他给出了常数 e 的定义，它是自然对数的底数，现在被称为欧拉数。

　　 欧拉还被认为是第一个发展图论的人（部分因为他解决了 “柯尼斯堡七桥问题”，这也被认为是拓扑学的第一个实际应用）。他还因解决多个未解的数论和分析学问题而声名远播，包括著名的巴塞尔问题。欧拉还被誉为发现了多面体的顶点和面数之和减去边数等于 2，这个数字现在被称为欧拉示性数。在物理学领域，欧拉将牛顿的物理定律重新表述为新的定律，并在他的两卷本著作《力学》中更好地解释了刚体的运动。他还为固体物体的弹性变形研究做出了重大贡献。

1. 早期生活

　　 莱昂哈德·欧拉于 1707 年 4 月 15 日出生在巴塞尔，父亲保罗三世·欧拉是改革宗教会的牧师，母亲玛格丽特（娘家姓布鲁克尔），她的祖先包括许多著名的古典学者。[16] 欧拉是家中的长子，下面有两个妹妹，安娜·玛利亚和玛利亚·玛格达莱娜，以及一个弟弟约翰·海因里希。[17][16] 在欧拉出生后不久，欧拉一家从巴塞尔搬到瑞士的里恩镇，父亲成为当地教堂的牧师，而欧拉则在这里度过了大部分童年。[16]

　　 从小，欧拉就接受了父亲的数学教育，父亲曾在巴塞尔大学向雅各布·伯努利学习过一些课程。大约在八岁时，欧拉被送到外祖母家生活，并在巴塞尔的拉丁学校就读。此外，他还接受了年轻神学家约翰内斯·布尔卡特的私人辅导，布尔卡特对数学有浓厚的兴趣。[16]

　　 1720 年，欧拉 13 岁时进入巴塞尔大学。[7] 在当时，年轻就读大学并不罕见。[16] 数学基础课程由已故的雅各布·伯努利的弟弟约翰·伯努利教授（雅各布·伯努利曾是欧拉父亲的老师）讲授。约翰·伯努利和欧拉很快熟识。欧拉在自传中描述了伯努利的教导：[18]

　　 “著名教授约翰·伯努利……特别乐意帮助我在数学科学上取得进展。然而，他由于日程繁忙，拒绝了私人的授课请求。然而，他给了我一个更为有益的建议，就是让我自己去掌握一些更为艰深的数学书籍，并以极大的勤奋把它们研读一遍，如果遇到疑难或困难，他每周六下午都会开放时间免费为我解答，他如此慷慨地评论我的问题，以至于当他解答我一个疑问时，十个疑问随之消失，这无疑是数学科学进步的最佳方法。”

　　 正是在这段时间里，在伯努利的支持下，欧拉得到了父亲的同意，决定成为一名数学家，而不是继续成为牧师。[19][20]

　　 1723 年，欧拉获得哲学硕士学位，并撰写了一篇论文，比较了笛卡尔和牛顿的哲学。[16] 此后，他又进入了巴塞尔大学的神学系。[20]

　　 1726 年，欧拉完成了一篇关于声音传播的论文《De Sono》[21][22]，试图通过这篇论文获得巴塞尔大学的职位，但未成功。[23] 1727 年，欧拉第一次参加了巴黎科学院的奖学金竞赛（该竞赛自 1720 年起每年举办，后来改为每两年一次）[24]。当年题目是寻找在船上最好的桅杆安放方式。皮埃尔·布盖，后被称为 “海军建筑学之父”，获得了第一名，欧拉则获得了第二名。[25] 在接下来的几年里，欧拉共参加了 15 次该竞赛，赢得了其中的 12 次。[24][25]

2. 职业生涯

圣彼得堡

图
图 1：1957 年苏联邮票，纪念欧拉 250 周年诞辰。邮票上的文字写道：“伟大数学家、院士莱昂哈德·欧拉诞辰 250 周年”。

　　 约翰·伯努利的两个儿子，丹尼尔和尼古劳斯，于 1725 年进入圣彼得堡的帝国俄罗斯科学院工作，并向欧拉保证，一旦有职位空缺，他们会推荐他。1726 年 7 月 31 日，尼古劳斯在俄罗斯逗留不到一年便因阑尾炎去世。当丹尼尔接替弟弟的位置，担任数学/物理学部门的职务时，他建议将他空出的生理学职位提供给他的朋友欧拉。1726 年 11 月，欧拉热切接受了这个提议，但他推迟了前往圣彼得堡的行程，因为他在未成功申请巴塞尔大学的物理学教授职位时，仍想争取机会。

　　 欧拉于 1727 年 5 月抵达圣彼得堡。他从科学院医务部门的初级职务晋升为数学部门的职位。他与丹尼尔·伯努利同住，并与其紧密合作。欧拉学会了俄语，适应了圣彼得堡的生活，并在俄罗斯海军担任医务职务。

　　 圣彼得堡的科学院由彼得大帝建立，旨在改善俄罗斯的教育水平，并弥补与西欧的科学差距。因此，它对外国学者，如欧拉，具有特别的吸引力。学院的赞助人凯瑟琳一世继续执行她已故丈夫的进步政策，但在欧拉到达圣彼得堡之前去世。随后，俄罗斯的保守派贵族在 12 岁彼得二世登基后获得了权力。贵族们对学院的外国科学家心存疑虑，削减了欧拉和他的同事们的资助，并禁止外国和非贵族学生进入中学和大学。

　　 1730 年彼得二世去世后，情况略有改善，受到德国影响的安娜·伊凡诺夫娜掌权。欧拉迅速在科学院中晋升，并于 1731 年被任命为物理学教授。他还离开了俄罗斯海军，拒绝了晋升为中尉的提议。两年后，丹尼尔·伯努利因受不了在圣彼得堡的审查和敌意，离开了巴塞尔。欧拉继任了数学系主任的职务。1734 年 1 月，他与乔治·格塞尔的女儿卡塔里娜·格塞尔结婚。

　　 1740 年，弗雷德里希二世曾试图招募欧拉加入他新成立的柏林科学院，但欧拉最初更愿意留在圣彼得堡。然而，在安娜皇后去世后，弗雷德里希二世同意支付他 1600 枚埃库（与欧拉在俄罗斯的薪水相同），欧拉同意前往柏林。1741 年，他请求离开圣彼得堡，前往柏林，理由是他的视力需要更温和的气候。俄罗斯科学院同意了他的请求，并将每年支付他 200 卢布，作为其积极成员之一。

柏林

　　 由于担心俄罗斯的持续动荡，欧拉于 1741 年 6 月离开圣彼得堡，接受了腓特烈大帝提供的柏林科学院职位。他在柏林生活了 25 年，期间写了数百篇文章。1748 年，他的《无穷分析引论》一书出版，1755 年，关于微分学的《微积分学原理》也出版了。1755 年，他被选为瑞典皇家科学院和法国科学院的外籍成员。欧拉在柏林的著名学生包括后来被认为是第一位俄罗斯天文学家的斯捷潘·鲁莫夫斯基。1748 年，欧拉拒绝了巴塞尔大学提供的继承已故约翰·伯努利的职位。1753 年，他在查尔滕堡购买了一座房子，与家人和寡母一起居住。

　　 欧拉成为了勃兰登堡-施韦德的弗里德里克·夏洛特的导师，这位公主是安哈尔特-德绍的弗雷德里克的侄女。1760 年代初，他向她写了超过 200 封信，这些信后来被编成《欧拉给德国公主的自然哲学信件》一书。该书内容涉及欧拉对物理学和数学的各种阐述，并为我们提供了对欧拉个性和宗教信仰的宝贵见解。此书被翻译成多种语言，在欧洲和美国出版，并且比他的任何数学著作更广为流传。《信件》的受欢迎程度证明了欧拉能够有效地向普通读者传达科学问题，这对一位专注于研究的科学家来说是一项罕见的能力。

　　 尽管欧拉为学会的声望做出了巨大贡献，并且曾被让·勒·朗·达朗贝尔推荐为学会会长候选人，但腓特烈二世最终自任会长。普鲁士国王在宫廷内有着庞大的知识分子圈子，他认为欧拉在数字和图形之外的事务上知识有限且不够精明。欧拉是一个简单、虔诚的宗教信徒，他从未质疑现有的社会秩序或传统信仰。在许多方面，他与伏尔泰截然相反，伏尔泰在腓特烈的宫廷中享有崇高的声望。欧拉不是一个擅长辩论的人，经常坚持讨论自己并不擅长的主题，这使得他成为伏尔泰讽刺的常客。腓特烈二世也曾对欧拉的工程实践能力感到失望，他曾说：

　　 “我曾想在我的花园里建一个喷水池：欧拉计算了将水泵送到水库所需的轮子力量，从水库通过渠道将水喷出到无忧宫。我的水轮是按几何学原理设计的，结果连水池附近五十步以内都无法扬起一口水。虚荣啊！几何的虚荣！”

　　 然而，从技术角度来看，这种失望几乎是没有根据的。欧拉的计算看起来是正确的，尽管他与腓特烈及建造喷泉的人们之间的互动可能存在问题。

　　 在柏林的这些年里，欧拉始终与圣彼得堡的科学院保持密切联系，并且在俄罗斯发表了 109 篇论文。他还帮助了圣彼得堡科学院的学生，并在他位于柏林的家中接待过俄罗斯的学生。1760 年，七年战争爆发，欧拉在查尔滕堡的农场被俄罗斯军队洗劫。得知此事后，伊凡·彼得罗维奇·萨尔季科夫将赔偿费用支付给欧拉，俄罗斯女皇伊丽莎白还额外支付了 4000 卢布——这在当时是巨额赔偿。欧拉决定于 1766 年离开柏林，返回俄罗斯。

　　 在柏林的这些年（1741-1766），欧拉处于生产力的巅峰时期。他写了 380 篇作品，其中 275 篇发表。这包括 125 篇柏林科学院的论文和超过 100 篇发送给圣彼得堡科学院的论文，后者仍然保留着他作为成员，并支付给他年薪。欧拉的《无穷分析引论》在 1748 年分两部分出版。除了个人研究，欧拉还管理着科学院的图书馆、天文台、植物园，并参与日历和地图的出版，这些都为科学院提供了收入。他甚至参与了无忧宫喷泉的设计工作。

返回俄罗斯

　　 在叶卡捷琳娜大帝即位后，俄罗斯的政治局势趋于稳定，因此在 1766 年，欧拉接受了邀请，返回圣彼得堡科学院。他的条件相当苛刻——年薪 3000 卢布、为妻子提供养老金，以及为他的儿子们提供高职保证。在大学里，他得到了学生安德斯·约翰·莱克塞尔的帮助。1771 年，欧拉在圣彼得堡的家被一场火灾摧毁。

3. 个人生活

　　 1734 年 1 月 7 日，欧拉与凯瑟琳娜·格塞尔（Katharina Gsell，1707-1773）结婚，她是圣彼得堡科学院画家乔治·格塞尔（Georg Gsell）的女儿。[33] 这对年轻夫妻在涅瓦河边购买了一栋房子。

　　 他们共有十三个孩子，其中只有五个活到了童年，[55] 包括三子两女。[56] 他们的第一个儿子是约翰·阿尔布雷希特·欧拉（Johann Albrecht Euler），他的教父是克里斯蒂安·戈尔巴赫（Christian Goldbach）。[56]

　　 在妻子于 1773 年去世三年后，[54] 欧拉与她的同母异父妹妹萨洛梅·阿比盖尔·格塞尔（Salome Abigail Gsell，1723-1794）结婚。[57] 这段婚姻持续到欧拉去世（1783 年）。

　　 他的兄弟约翰·海因里希于 1735 年定居圣彼得堡，并在学院担任画家。[34]

　　 欧拉年轻时背诵了维吉尔的《埃涅阿斯纪》全诗，年老时他能够完整地背诵整首诗，并且能够准确说出他所学版本中每一页的第一句和最后一句。[58][59]

视力恶化

　　 欧拉的视力在他的数学生涯中逐渐恶化。1738 年，在几乎因高热而去世三年后，[60] 他几乎失去了右眼的视力。欧拉将自己视力受损的原因归咎于他为圣彼得堡科学院绘制的地图，[61] 但导致他失明的具体原因仍然是一个猜测的问题。[62][63] 在德国期间，欧拉右眼的视力持续恶化，以至于弗雷德里克称他为 “独眼巨人”（Cyclops）。欧拉对于视力丧失作出评论时表示：“现在我将有更少的干扰。”[61] 1766 年，他的左眼被发现有白内障。虽然通过治疗暂时改善了他的视力，但并发症最终使他左眼几乎完全失明。[39] 然而，这一状况似乎对他的工作产出几乎没有影响。在抄写员的帮助下，欧拉在多个学科的工作产出反而有所增加；[64] 到 1775 年，他平均每周就能完成一篇数学论文。[39]

去世

　　 1783 年 9 月 18 日，在圣彼得堡，欧拉与家人共进午餐后，正与安德烈·约翰·莱克塞尔讨论新发现的天王星及其轨道时，突然倒下并因脑溢血去世。[62] 雅各布·冯·斯泰林为俄罗斯科学院写了一篇简短的讣告，而欧拉的弟子之一，俄罗斯数学家尼古拉·福斯，则写了一篇更为详细的悼词，并在纪念会中发表了这篇悼词。[55] 法国数学家和哲学家马尔基·德·孔多塞尔在为法国科学院所写的悼文中说道：

图
图 2：欧拉的墓位于亚历山大·涅夫斯基修道院

　　 他停止了计算，也停止了生活—— ... he ceased to calculate and to live.[65]

　　 欧拉被埋葬在斯莫尔南斯克路德教墓地，位于瓦西里岛，与卡塔琳娜同葬。1837 年，俄罗斯科学院为他安装了新的纪念碑，替换了那块已被植物覆盖的墓碑。为了纪念欧拉诞辰 250 周年，1957 年，他的墓被迁移至亚历山大·涅夫斯基修道院的拉扎列夫墓地。[66]

4. 数学和物理学的贡献

　　 欧拉几乎涉及了数学的所有领域，包括几何学、微积分、三角学、代数学和数论，以及连续介质物理学、月球理论和其他物理学领域。他是数学史上的奠基人物；如果将他的著作全部印刷出来，这些作品（其中许多是基础性的重要著作）将占据 60 到 80 卷四开本的篇幅。[39] 欧拉的名字与大量的课题相关联。从 1725 年到 1783 年，欧拉的工作年均达到 800 页。他还写了超过 4500 封信件和数百篇手稿。据估计，欧拉是 18 世纪数学、物理学、力学、天文学和航海学的四分之一著作的作者。[14]

数学符号

　　 欧拉通过他大量的教材引入并推广了几种符号惯例。最著名的是，他引入了函数的概念，并首次使用 \( f(x) \) 来表示函数 \( f \) 作用于自变量 \( x \)。他还引入了现代三角函数的符号、自然对数的底数 \( e \)（现在也称为欧拉数）、希腊字母 \( \Sigma \) 来表示求和以及字母 \( i \) 来表示虚数单位。[67] 希腊字母 \( \pi \) 用来表示圆的周长与直径的比值，也是欧拉所推广的，尽管最初是由威尔士数学家威廉·琼斯提出的。[68]

分析

　　 无穷小微积分的发展是 18 世纪数学研究的前沿，伯努利家族——欧拉的家庭朋友——为该领域的早期进展做出了许多贡献。由于他们的影响，学习微积分成为欧拉工作的主要焦点。尽管欧拉的一些证明在现代数学严谨性标准下无法接受[69]（特别是他对代数普遍性的依赖），但他的思想促成了许多重大进展。欧拉在分析学中以频繁使用并发展幂级数而著名，幂级数是将函数表示为无限项之和，[70] 如： \[ e^{x}=\sum_{n=0}^{\infty} \frac{x^n}{n!} = \lim_{n \to \infty} \left( \frac{1}{0!} + \frac{x}{1!} + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!} \right)~ \] 欧拉使用幂级数使他能够解决巴塞尔问题，即求所有自然数平方倒数的和，这一问题他在 1735 年解决（并在 1741 年给出了更为详尽的证明）。巴塞尔问题最初由皮耶特罗·门戈利在 1644 年提出，到了 1730 年代已成为一个著名的开放问题，被雅各布·伯努利推崇，并被当时许多顶尖数学家尝试解决但未成功。欧拉发现： \[ \sum_{n=1}^{\infty} \frac{1}{n^2} = \lim_{n \to \infty} \left( \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots + \frac{1}{n^2} \right) = \frac{\pi^2}{6}~ \] 欧拉还引入了常数： \[ \gamma = \lim_{n \to \infty} \left( 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{n} - \ln\left(n\right) \right) \approx 0.5772~ \] 这个常数现在被称为欧拉常数或欧拉-马谢罗尼常数，并研究了它与调和级数、伽玛函数和黎曼ζ函数值之间的关系。[73]

图
图 3：欧拉公式的几何解释

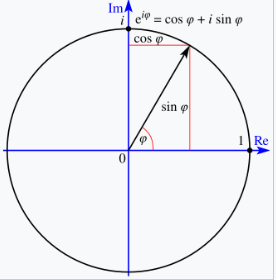
　　 欧拉引入了指数函数和对数在解析证明中的使用。他发现了用幂级数表示各种对数函数的方法，并成功地定义了负数和复数的对数，从而极大地扩展了对数在数学应用中的范围。[67] 他还为复数定义了指数函数，并发现它与三角函数之间的关系。对于任何实数 φ（取弧度），欧拉公式表明复指数函数满足： \[ e^{i\varphi} = \cos \varphi + i \sin \varphi~ \] 理查德·费曼称这公式为 “数学中最著名的公式”。[74]

　　 上述公式的一个特例被称为欧拉恒等式： \[ e^{i\pi} + 1 = 0~ \] 欧拉通过引入伽玛函数[75][76]，阐述了高阶超越函数的理论，并为解决四次方程引入了一种新方法。[77] 他找到了一种计算具有复数极限的积分的方法，预示着现代复分析的发展。他发明了变分法，并为在这一领域中将优化问题转化为微分方程的解，提出了欧拉-拉格朗日方程。

　　 欧拉率先使用解析方法来解决数论问题。通过这一工作，他将数学的两个不同分支结合在一起，创造了一个新的研究领域——解析数论。在为这一新领域奠定基础时，欧拉创建了超几何级数、q 级数、双曲三角函数和连分数的解析理论。例如，他利用调和级数的发散性证明了素数的无限性，并使用解析方法对素数的分布规律进行了初步探索。欧拉在这一领域的工作促成了素数定理的发展。[78]

数论

　　 欧拉对数论的兴趣可以追溯到他在圣彼得堡科学院的朋友克里斯蒂安·高尔巴赫的影响。[79] 欧拉在数论方面的早期工作主要基于皮埃尔·德·费尔马的研究。欧拉发展了费尔马的一些思想，并驳斥了他的一些猜想，例如费尔马猜想的形式为 \(2^{2^{n}} + 1\)（费尔马数）是素数的猜想。[80]

　　 欧拉将素数分布的性质与分析中的一些思想联系起来。他证明了素数的倒数之和是发散的。通过这一过程，他发现了黎曼ζ函数与素数之间的关系，这被称为黎曼ζ函数的欧拉积公式。[81]

　　 欧拉发明了欧拉φ函数 \( \phi(n) \)，表示小于或等于整数 n 且与 n 互质的正整数的个数。利用这个函数的性质，他将费尔马小定理推广为现在所称的欧拉定理。[82] 他对完美数的理论作出了重要贡献，完美数自欧几里得以来就吸引着数学家的关注。他证明了偶完美数与梅森素数之间的关系是一一对应的，这一结果被称为欧几里得-欧拉定理。[83] 欧拉还猜想了二次互反律。这一概念被视为数论中的基本定理，他的思想为卡尔·弗里德里希·高斯的工作，特别是《算术研究》奠定了基础。[84] 到 1772 年，欧拉已证明 \( 2^{31} - 1 = 2,147,483,647 \) 是一个梅森素数，这可能是直到 1867 年为止已知的最大素数。[85]

　　 欧拉还对整数划分理论作出了重要贡献。[86]

图论

图
图 4：欧拉时代柯尼斯堡的地图，展示了七座桥的实际布局，突出显示了普雷格尔河及其桥梁。

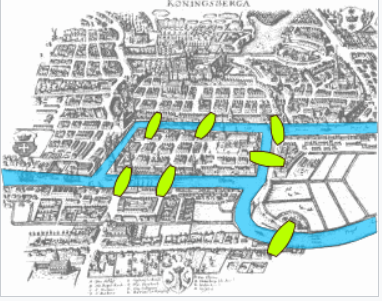
　　 在 1735 年，欧拉提出了解决 “柯尼斯堡七桥问题” 的方案。[87] 这座普鲁士的柯尼斯堡市位于普雷格尔河上，市区包括两个大岛，这些岛屿通过七座桥梁与彼此及大陆连接。问题是要决定是否有可能找到一条路径，使得每座桥都被正好跨越一次，并最终回到起点。答案是否定的：没有欧拉回路。这个解法被认为是图论的第一个定理。[87]

　　 欧拉还发现了一个公式 \( V - E + F = 2 \) 它描述了一个凸多面体的顶点数、边数和面数之间的关系，[88] 因此也适用于平面图。这个公式中的常数现在被称为图（或其他数学对象）的欧拉示性数，它与该对象的属（genus）有关。[89] 这一公式的研究和推广，特别是由柯西[90] 和吕伊耶[91] 完成，标志着拓扑学的诞生。[88]

物理学、天文学和工程学

　　 欧拉的伟大成就之一是在分析解决现实世界问题方面，以及描述伯努利数、傅里叶级数、欧拉数、常数 e 和π、连分数和积分的众多应用。他将莱布尼茨的微分学与牛顿的流量法结合起来，并开发了使微积分能够更容易地应用于物理问题的工具。他在提高积分的数值近似方面取得了巨大进展，发明了如今被称为欧拉近似法的工具。最著名的这些近似方法包括欧拉法[92]和欧拉-麦克劳林公式[93][94][95]。

　　 欧拉帮助发展了欧拉-伯努利梁方程，这成为工程学的基石之一。[96] 除了成功地将他的分析工具应用于经典力学问题外，欧拉还将这些技术应用于天文学问题。他在天文学方面的成就通过多次巴黎科学院奖项得到了认可。他的贡献包括非常准确地确定彗星和其他天体的轨道、理解彗星的性质以及计算太阳的视差。他的计算为精确的经度表的发展做出了贡献。[97]

　　 欧拉在光学方面也做出了重要贡献。[98] 他与牛顿的光的粒子说理论[99]（当时的主流理论）有分歧。他在 1740 年代关于光学的论文帮助确保了克里斯蒂安·惠更斯提出的光的波动理论成为主流思维模式，至少在量子光学理论发展之前是如此。[100]

　　 在流体动力学方面，欧拉是第一个预测空化现象的人，发生在 1754 年，比 19 世纪末首次观测到空化现象还要早，并且用于流体流动计算的欧拉数源自他关于涡轮效率的相关研究。[101] 1757 年，他发布了一套关于无粘流动的方程，现在被称为欧拉方程。[102]

　　 欧拉在结构工程学中以给出欧拉临界荷载公式而闻名，这个公式计算理想支撑物的临界屈曲荷载，它仅依赖于支撑物的长度和弯曲刚度。[103]

逻辑

图
图 5：欧拉图

　　 欧拉被认为是第一个使用闭合曲线来说明三段论推理的人（1768 年）。这些图示后来被称为欧拉图。[104]

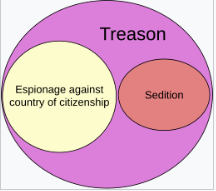
　　 欧拉图是一种用来表示集合及其关系的图示方法。欧拉图由平面上的简单闭合曲线（通常是圆形）组成，这些曲线表示集合。每条欧拉曲线将平面划分为两个区域或 “区域”：内部区域象征性地代表集合的元素，外部区域代表所有不属于该集合的元素。曲线的大小或形状并不重要；图示的意义在于它们的重叠方式。每条曲线所界定的区域之间的空间关系（重叠、包含或都不是）对应于集合论中的关系（交集、子集和互斥性）。如果两条曲线的内部区域没有交集，则表示这两个集合是互斥的；如果两条曲线的内部区域有交集，则表示这两个集合有共同的元素；位于两条曲线内部的区域表示这两个集合的交集。如果一条曲线完全包含在另一条曲线的内部区域中，则表示它是另一个集合的子集。

　　 欧拉图（及其改进版维恩图）作为集合论教学的一部分，在 1960 年代的 “新数学” 运动中被纳入课程教学。从那时起，它们作为一种可视化特征组合的方式被广泛应用。[105][106]

音乐

　　 欧拉的一大非凡兴趣是将数学思想应用于音乐。1739 年，他撰写了《音乐新理论的尝试》（*Tentamen novae theoriae musicae*），希望将音乐理论最终纳入数学的一部分。然而，这部分工作未获得广泛关注，有人评价其 “对音乐家来说过于数学化，对数学家来说又过于音乐化”。[107] 即使在处理音乐时，欧拉的方式主要是数学化的，例如他通过二进制对数来描述八度音程划分为分数部分的方式。[109] 欧拉在音乐方面的著作并不算多（几百页，在他总共约三万页的作品中占较小比例），但它们反映了他早期的关注，并贯穿了他的一生。[108]

　　 欧拉音乐理论的一个起点是对 “体裁”（*genres*）的定义，即使用素数 3 和 5 划分八度音程的可能方式。他描述了 18 种这样的体裁，其一般定义为 \( 2^m A \)，其中 \( A \) 是体裁的 “指数”（即 3 和 5 的指数之和），而 \( 2^m \)（“\( m \)” 可以是任意大小的数，只要声音可以感知”[110]）表示这种关系独立于涉及的八度数量。第一个体裁，\( A = 1 \)，是八度本身（或其重复）；第二个体裁，\( 2^m \cdot 3 \)，是八度按五度分割（五度加四度，C–G–C）；第三个体裁是 \( 2^m \cdot 5 \)，即大三度加小六度（C–E–C）；第四个体裁是 \( 2^m \cdot 3^2 \)，即两个四度和一个全音（C–F–B♭–C）；第五个体裁是 \( 2^m \cdot 3 \cdot 5 \)（C–E–G–B–C）等等。第 12 种体裁（\( 2^m \cdot 3^3 \cdot 5 \)）、第 13 种体裁（\( 2^m \cdot 3^2 \cdot 5^2 \)）和第 14 种体裁（\( 2^m \cdot 3 \cdot 5^3 \)）分别是古代调式中的自然音阶、半音阶和等音程的修正版本。第 18 种体裁（\( 2^m \cdot 3^3 \cdot 5^2 \)）被称为 “自然-半音阶”（*diatonico-chromatic*），“一般用于所有作品中”，并被发现与约翰·马特森（Johann Mattheson）描述的体系相同。[111][112] 后来，欧拉设想了包含素数 7 的体裁描述的可能性。[113]

　　 欧拉设计了一种特定的图示，称为 *Speculum musicum*，用于展示自然-半音阶体裁，并讨论了该图中表示特定音程的路径，这与他对柯尼斯堡七桥问题的兴趣相呼应（见上文）。这种工具在新黎曼理论中作为 *Tonnetz* 再次引起了兴趣（另见音乐中的晶格结构）。[116]

　　 欧拉进一步利用 “指数” 原理，提出了一种从素因数推导音程和和弦的 “和谐度”（*gradus suavitatis*，即愉悦度）的方法——需要注意的是，他只考虑纯律（即 1 以及素数 3 和 5）。[117] 这一系统已被推广为适用于任意素数的公式，例如以下形式： \[ ds = \sum_{i} (k_i p_i - k_i) + 1~ \] 其中 \( p_i \) 是素数，\( k_i \) 是其指数。[118]

5. 个人哲学与宗教信仰

　　 欧拉终其一生是一个虔诚的宗教信徒。[20] 关于欧拉宗教信仰的很多内容，可以通过他的《致一位德国公主的信》和他的早期作品《救赎神圣启示，反对自由思想者的异议》（*Rettung der Göttlichen Offenbahrung gegen die Einwürfe der Freygeister*）来推断。这些作品表明，欧拉是一个虔诚的基督徒，相信《圣经》是神所启示的；《救赎》主要是论证圣经的神圣启示。[119][120]

　　 欧拉反对莱布尼茨的单子论和克里斯蒂安·沃尔夫的哲学。[121] 欧拉坚信，知识一部分是基于精确的定量法则，而单子论和沃尔夫学说无法提供这种基础。欧拉还将沃尔夫的观点标记为 “异教和无神论的”。[122]

　　 有一个著名的传说[123]，源自欧拉与世俗哲学家在宗教问题上的争论，故事发生在欧拉第二次担任圣彼得堡科学院期间。法国哲学家丹尼斯·狄德罗应叶卡捷琳娜大帝的邀请访问俄罗斯。然而，皇后担心哲学家提出的无神论论点正在影响宫廷成员，于是请欧拉与这位法国人对话。狄德罗被告知，一位博学的数学家已提供了一种证明上帝存在的证明：他同意在宫廷上观看这一证明。欧拉出现，走向狄德罗，以充满信念的语气宣布了这句话： “先生， \[ \frac{a+b^n}{n} = x, \text{因此上帝存在——回答！}~ \]” 传说中，狄德罗（故事称）认为所有数学都是胡言乱语，他站在那儿愣住了，宫廷中爆发出阵阵笑声。狄德罗感到尴尬，要求离开俄罗斯，叶卡捷琳娜皇后优雅地同意了他的请求。尽管这个轶事很有趣，但它是虚构的，因为狄德罗本人也做过数学研究。[124] 这个传说似乎最早由迪厄多内·提博（Dieudonné Thiébault）讲述，并由奥古斯图斯·德·摩根（Augustus De Morgan）进行了润色。[123]

6. 纪念活动

图
图 6：欧拉肖像出现在瑞士第六系列 10 法郎纸币上

　　 欧拉曾出现在瑞士 10 法郎纸币的第六[125]和第七[126]系列上，并且还出现在多枚瑞士、德国和俄罗斯的邮票上。1782 年，他被选为美国艺术与科学院的外籍荣誉会员。[127] 小行星 2002 Euler 以他的名字命名。[128]

7. 精选书目

图
图 7：欧拉肖像出现在瑞士 10 法郎纸币第七系列上

　　 欧拉的著作非常丰富，以下是其中一些书籍：

　　 直到 1830 年，欧拉的绝大部分遗作才开始单独出版，[135] 之后，保罗·海因里希·冯·弗斯（欧拉的曾孙、尼古拉斯·弗斯的儿子）发现了另外 61 篇未出版的作品，并于 1862 年作为合集出版。[135][136] 瑞典数学家古斯塔夫·恩斯特朗于 1910 至 1913 年间编制了欧拉作品的编年目录。[137] 该目录称为 “恩斯特朗索引”，将欧拉的作品编号从 E1 到 E866。[138] 欧拉档案馆最初设立于达特茅斯学院[139]，之后转移到美国数学协会[140]，最新则位于太平洋大学，成立于 2017 年。[141]

　　 1907 年，瑞士科学院成立了欧拉委员会，负责出版欧拉全集。经过 19 世纪的多次延迟，[135]《欧拉全集》第一卷终于于 1911 年出版。[142] 然而，新手稿的发现不断增加了这一项目的规模。幸运的是，《欧拉全集》的出版稳步推进，截至 2006 年，已出版超过 70 卷（每卷平均 426 页），到 2022 年已出版 80 卷。[143][12][14] 这些卷分为四个系列。第一系列汇集了关于分析、代数和数论的作品，共 29 卷，超过 14,000 页。第二系列 31 卷，约 10,660 页，包含了力学、天文学和工程学的作品。第三系列包含了 12 卷关于物理学的作品。第四系列包含了大量的欧拉通信、未出版手稿和笔记，该系列的编纂始于 1967 年。经过 8 卷的出版后，该项目决定从 2022 年起，将第四系列剩余的预计卷册以在线格式出版。[12][142][14]

8. 注释

  1. 欧拉被列为拉格朗日的博士导师等同人物。[1]
  2. 发音/ˈjuːlər/（YOO-lər）被认为是错误的。[2][3][4][5]
  3. 这句话出现在古列尔莫·利布里的评论中，评论的是一部关于 18 世纪数学家通信的最新出版合集：“…我们会回忆起拉普拉斯本人，…他不断地对年轻数学家重复这些我们从他自己口中听到的名言：‘读欧拉，读欧拉，他是我们所有人的大师。’”[144]
  4. 这句话出现在高斯写给保罗·福斯的信中，信件日期为 1849 年 9 月 11 日：[10] “小欧拉论文的特别出版无疑是非常值得称赞的，[…] 而对所有欧拉作品的学习，永远是各数学领域中最好的学校，任何其他方式无法替代。”

9. 参考文献

  1. Leonhard Euler 在数学家谱项目中，检索日期：2021 年 7 月 2 日；已存档
  2. "Euler". 《牛津英语词典》（第二版）。牛津大学出版社，1989 年。
  3. "Euler". Merriam–Webster's Online Dictionary，2009 年。2009 年 4 月 25 日原文存档，检索日期：2009 年 6 月 5 日。
  4. "Euler, Leonhard". 《美国传统英语词典》（第五版）。波士顿：霍顿·米夫林公司，2011 年。2013 年 10 月 4 日原文存档，检索日期：2013 年 5 月 30 日。
  5. Higgins, Peter M. (2007)。*Nets, Puzzles, and Postmen: An Exploration of Mathematical Connections*。牛津大学出版社，第 43 页。ISBN 978-0-19-921842-4。
  6. Dunham, William (1999)，第 17 页。
  7. Debnath, Lokenath (2010)。*The Legacy of Leonhard Euler: A Tricentennial Tribute*。伦敦：帝国理工大学出版社，第 vii 页。ISBN 978-1-84816-525-0。
  8. Dunham, William (1999)，第 xiii 页。"Lisez Euler, lisez Euler, c'est notre maître à tous."
  9. Grinstein, Louise; Lipsey, Sally I. (2001)。"Euler, Leonhard (1707–1783)"。*数学教育百科全书*。劳特利奇出版社，第 235 页。ISBN 978-0-415-76368-4。
  10. Fuß, Paul Heinrich; Gauß, Carl Friedrich (1849 年 9 月 11 日)。"Carl Friedrich Gauß → Paul Heinrich Fuß, Göttingen, 1849 年 9 月 11 日"。
  11. "Leonhardi Euleri Opera Omnia (LEOO)"。Bernoulli Euler Center。原文存档于 2022 年 9 月 11 日，检索日期：2022 年 9 月 11 日。
  12. "The works"。Bernoulli-Euler Society。原文存档于 2022 年 9 月 11 日，检索日期：2022 年 9 月 11 日。
  13. Gautschi, Walter (2008)，第 3 页。
  14. Assad, Arjang A. (2007)。"Leonhard Euler: A brief appreciation"。*Networks*，49(3): 190–198。doi:10.1002/net.20158。S2CID 11298706。
  15. Boyer, Carl B. (2021 年 6 月 1 日)。"Leonhard Euler"。*大英百科全书*。原文存档于 2021 年 5 月 3 日，检索日期：2021 年 5 月 27 日。
  16. Gautschi, Walter (2008)，第 4 页。
  17. Calinger, Ronald (2016)，第 11 页。
  18. Gautschi, Walter (2008)，第 5 页。
  19. Calinger, Ronald (1996)，第 124 页。
  20. Knobloch, Eberhard; Louhivaara, I. S.; Winkler, J.（主编）（1983 年 5 月）。*Zum Werk Leonhard Eulers: Vorträge des Euler-Kolloquiums im Mai 1983 in Berlin*（PDF）。Birkhäuser Verlag。doi:10.1007/978-3-0348-7121-1。ISBN 978-3-0348-7122-8。
  21. Calinger, Ronald (2016)，第 32 页。
  22. Euler, Leonhard (1727)。*Dissertatio physica de sono* [《关于声音的物理学论文》]（拉丁文）。巴塞尔：E. 和 J. R. Thurnisiorum。原文存档于 2021 年 6 月 6 日，检索日期：2021 年 6 月 6 日 – 通过 Euler 档案。 英文翻译：Bruce, Ian。"Euler's Dissertation De Sono : E002"（PDF）。*Some Mathematical Works of the 17th & 18th Centuries, including Newton's Principia, Euler's Mechanica, Introductio in Analysin, etc.*, 主要从拉丁文翻译成英文。原文存档（PDF）于 2016 年 6 月 10 日，检索日期：2021 年 6 月 12 日。
  23. Calinger, Ronald (1996)，第 125 页。
  24. Calinger, Ronald (1996)，第 125 页。 "The Paris Academy"。Euler 档案。美国数学协会。原文存档于 2021 年 7 月 30 日，检索日期：2021 年 7 月 29 日。
  25. Calinger, Ronald (1996)，第 156 页。
  26. Calinger, Ronald (1996)，第 121–166 页。
  27. O'Connor, John J.; Robertson, Edmund F. "Nicolaus (II) Bernoulli"。*MacTutor Mathematics History Archive*。圣安德鲁斯大学。检索日期：2021 年 7 月 2 日。
  28. Calinger, Ronald (1996)，第 126–127 页。
  29. Calinger, Ronald (1996)，第 127 页。
  30. Calinger, Ronald (1996)，第 126 页。
  31. Calinger, Ronald (1996)，第 128 页。
  32. Calinger, Ronald (1996)，第 128–129 页。
  33. Gekker & Euler (2007)，第 402 页。
  34. Calinger, Ronald (1996)，第 157–158 页。
  35. Gautschi, Walter (2008)，第 7 页。
  36. Euler, Leonhard (1787)。*"Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum"* [《微积分基础，及其在有限分析和级数中的应用》]。圣彼得堡帝国科学院（拉丁文）。第 1 卷。Petri Galeatii：1–880。原文存档于 2021 年 5 月 6 日，检索日期：2021 年 6 月 8 日 – 通过 Euler 档案。
  37. Dunham, William (1999)，第 xxiv–xxv 页。
  38. Stén, Johan C.-E. (2014)。*"Academic events in Saint Petersburg"*。*A Comet of the Enlightenment*。*Vita Mathematica*，第 17 卷。Birkhäuser 出版社，第 119–135 页。doi:10.1007/978-3-319-00618-5_7。ISBN 978-3-319-00617-8。特别请参见第 37 脚注，第 131 页。
  39. Finkel, B. F. (1897)。*"Biography – Leonhard Euler"*。*The American Mathematical Monthly*，第 4 卷，第 12 期，297–302 页。doi:10.2307/2968971。JSTOR 2968971。MR 1514436。
  40. Trimble, Virginia；Williams, Thomas；Bracher, Katherine；Jarrell, Richard；Marché, Jordan D.；Ragep, F. Jamil, 编 (2007)。*Biographical Encyclopedia of Astronomers*。Springer Science+Business Media，第 992 页。ISBN 978-0-387-30400-7。可在 Archive.org 查看。
  41. Clark, William; Golinski, Jan; Schaffer, Simon (1999)。*The Sciences in Enlightened Europe*。芝加哥大学出版社，第 395 页。ISBN 978-0-226-10940-4。原文存档于 2021 年 4 月 22 日，检索日期：2021 年 6 月 15 日。
  42. Knobloch, Eberhard (2007)。*"Leonhard Euler 1707–1783. Zum 300. Geburtstag eines langjährigen Wahlberliners"*。*Mitteilungen der Deutschen Mathematiker-Vereinigung*，第 15 卷，第 4 期，276–288 页。doi:10.1515/dmvm-2007-0092。S2CID 122271644。
  43. Gautschi, Walter (2008)，第 8–9 页。
  44. Euler, Leonhard (1802)。*Letters of Euler on Different Subjects of Physics and Philosophy, Addressed to a German Princess*。由 Hunter, Henry 翻译（第 2 版）。伦敦：Murray and Highley。通过互联网档案存档。
  45. Frederick II of Prussia (1927)。*Letters of Voltaire and Frederick the Great*，信件 H 7434，1778 年 1 月 25 日。Richard Aldington 编。纽约：Brentano's。
  46. Lynch, Peter (2017 年 9 月)。*"Euler and the failed fountain of Sanssouci — that's maths: Frederick the Great ignored the advice of a genius in maths and physics"*。*Irish Times*。检索日期：2023 年 12 月 26 日。
  47. Vucinich, Alexander (1960)。*"Mathematics in Russian Culture"*。*Journal of the History of Ideas*，第 21 卷，第 2 期，164–165 页。doi:10.2307/2708192。ISSN 0022-5037。JSTOR 2708192。原文存档于 2021 年 8 月 3 日，检索日期：2021 年 8 月 3 日。
  48. Gindikin, Simon (2007)。*"Leonhard Euler"*。*Tales of Mathematicians and Physicists*。Springer 出版社，第 171–212 页。doi:10.1007/978-0-387-48811-0_7。ISBN 978-0-387-48811-0。特别请参见第 182 页，原文存档于 2021 年 6 月 10 日，通过 Wayback Machine 查看。
  49. Gautschi, Walter (2008)，第 9 页。
  50. Knobloch, Eberhard (1998)。*"Mathematics at the Prussian Academy of Sciences 1700–1810"*。收录于 Begehr, Heinrich; Koch, Helmut; Kramer, Jürg; Schappacher, Norbert; Thiele, Ernst-Jochen（编）*Mathematics in Berlin*。巴塞尔：Birkhäuser Basel，第 1–8 页。doi:10.1007/978-3-0348-8787-8_1。ISBN 978-3-7643-5943-0。
  51. Thiele, Rüdiger (2005)。*"The Mathematics and Science of Leonhard Euler (1707–1783)"*。收录于*Mathematics and the Historian's Craft*。CMS 数学书籍系列。纽约：Springer Publishing，第 81–140 页。doi:10.1007/0-387-28272-6_6。ISBN 978-0-387-25284-1。
  52. Eckert, Michael (2002)。*"Euler and the Fountains of Sanssouci"*。*Archive for History of Exact Sciences*，56(6)：451–468 页。doi:10.1007/s004070200054。ISSN 0003-9519。S2CID 121790508。
  53. Maehara, Hiroshi; Martini, Horst (2017)。*"On Lexell's Theorem"*。*The American Mathematical Monthly*，124(4)：337–344 页。doi:10.4169/amer.math.monthly.124.4.337。ISSN 0002-9890。JSTOR 10.4169/amer.math.monthly.124.4.337。S2CID 125175471。原文存档于 2021 年 8 月 20 日，检索日期：2021 年 6 月 16 日。
  54. Thiele, Rüdiger (2005)。*"The mathematics and science of Leonhard Euler"*。收录于 Kinyon, Michael; van Brummelen, Glen（编）*Mathematics and the Historian's Craft: The Kenneth O. May Lectures*。Springer Publishing，第 81–140 页。ISBN 978-0-387-25284-1。
  55. Fuss, Nicolas (1783)。*"Éloge de M. Léonhard Euler"* [为莱昂哈德·欧拉的颂词]。*Nova Acta Academiae Scientiarum Imperialis Petropolitanae*（法语），1：159–212 页。原文存档于 2021 年 8 月 20 日，检索日期：2018 年 5 月 19 日，来自 *Bioheritage Diversity Library*。该文的英文翻译为 *"Eulogy of Leonhard Euler by Nicolas Fuss"*，出自 *MacTutor History of Mathematics archive*。翻译者：John S. D. Glaus，圣安德鲁斯大学。原文存档于 2018 年 12 月 26 日，检索日期：2006 年 8 月 30 日。
  56. Calinger 1996，第 129 页。
  57. Gekker & Euler 2007，第 405 页。
  58. Meade, Phil (1999 年 11 月 27 日)。*"Letter: Uncommon talent"*，www.newscientist.com。检索日期：2024 年 9 月 22 日。
  59. Nahin, Paul J. (2017)。*Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills*。普林斯顿科学文库。普林斯顿牛津：普林斯顿大学出版社，第 326 页。ISBN 978-0-691-17591-1。
  60. Gautschi 2008，第 6 页。
  61. Eves, Howard W. (1969)。*"Euler's blindness"*，收录于 *Mathematical Circles: A Selection of Mathematical Stories and Anecdotes, Quadrants III and IV*。Prindle, Weber, & Schmidt，第 48 页。OCLC 260534353。该引用也出现在 Richeson（2012 年），第 17 页，原文存档于 2021 年 6 月 16 日，来自 Eves。
  62. Asensi, Victor; Asensi, Jose M. (2013 年 3 月)。*"Euler's right eye: the dark side of a bright scientist"*。*Clinical Infectious Diseases*，57(1)：158–159 页。doi:10.1093/cid/cit170。PMID 23487386。
  63. Bullock, John D.; Warwar, Ronald E.; Hawley, H. Bradford (2022 年 4 月)。*"Why was Leonhard Euler blind?"*。*British Journal for the History of Mathematics*，37：24–42 页。doi:10.1080/26375451.2022.2052493。S2CID 247868159。
  64. Gautschi 2008，第 9-10 页。
  65. Marquis de Condorcet。*“Eulogy of Euler – Condorcet”*。原文存档于 2006 年 9 月 16 日，检索日期：2006 年 8 月 30 日。
  66. Calinger 2016，第 530-536 页。
  67. Boyer, Carl B.; Merzbach, Uta C. (1991)。*A History of Mathematics*。约翰·威利父子公司，第 439-445 页。ISBN 978-0-471-54397-8。
  68. Arndt, Jörg; Haenel, Christoph (2006)。*Pi Unleashed*。施普林格出版社，第 166 页。ISBN 978-3-540-66572-4。原文存档于 2021 年 6 月 17 日，检索日期：2021 年 6 月 8 日。
  69. Wanner, Gerhard; Hairer, Ernst (2005)。*Analysis by its history*（第 1 版）。施普林格出版社，第 63 页。ISBN 978-0-387-77036-9。
  70. Ferraro 2008，第 155 页。
  71. Morris, Imogen I. (2023 年 10 月 24 日)。*Mechanising Euler's use of Infinitesimals in the Proof of the Basel Problem*（博士论文）。爱丁堡大学。doi
  72. Dunham 1999。
  73. Lagarias, Jeffrey C. (2013 年 10 月)。*“Euler's constant: Euler's work and modern developments”*。*Bulletin of the American Mathematical Society*，50(4)：556 页。arXiv:1303.1856。doi:10.1090/s0273-0979-2013-01423-x。MR 3090422。S2CID 119612431。
  74. Feynman, Richard (1970)。*“Chapter 22: Algebra”*，*The Feynman Lectures on Physics*，第 1 卷，第 10 页。
  75. Ferraro 2008，第 159 页。
  76. Davis, Philip J. (1959). "Leonhard Euler's integral: A historical profile of the gamma function". *The American Mathematical Monthly*. 66: 849–869. doi:10.2307/2309786. JSTOR 2309786. MR 0106810.
  77. Nickalls, R. W. D. (March 2009). "The quartic equation: invariants and Euler's solution revealed". *The Mathematical Gazette*. 93 (526): 66–75. doi:10.1017/S0025557200184190. JSTOR 40378672. S2CID 16741834.
  78. Dunham 1999, Ch. 3, Ch. 4.
  79. Calinger 1996, p. 130.
  80. Dunham 1999, p. 7.
  81. Patterson, S. J. (1988). *An introduction to the theory of the Riemann zeta-function*. Cambridge Studies in Advanced Mathematics. Vol. 14. Cambridge: Cambridge University Press. p. 1. doi:10.1017/CBO9780511623707. ISBN 978-0-521-33535-5. MR 0933558. Archived from the original on 18 June 2021. Retrieved 6 June 2021.
  82. Shiu, Peter (November 2007). "Euler's contribution to number theory". *The Mathematical Gazette*. 91 (522): 453–461. doi:10.1017/S0025557200182099. JSTOR 40378418. S2CID 125064003.
  83. Stillwell, John (2010). *Mathematics and Its History*. Undergraduate Texts in Mathematics. Springer. p. 40. ISBN 978-1-4419-6052-8. Archived from the original on 27 July 2021. Retrieved 6 June 2021.
  84. Dunham 1999, Ch. 1, Ch. 4.
  85. Caldwell, Chris. "The largest known prime by year". *PrimePages*. University of Tennessee at Martin. Archived from the original on 8 August 2013. Retrieved 9 June 2021.
  86. Hopkins, Brian; Wilson, Robin (2007). "Euler's science of combinations". *Leonhard Euler: Life, Work and Legacy*. Stud. Hist. Philos. Math. Vol. 5. Amsterdam: Elsevier. pp. 395–408. MR 3890500.
  87. Alexanderson, Gerald (July 2006). "Euler and Königsberg's bridges: a historical view". *Bulletin of the American Mathematical Society*. 43 (4): 567. doi:10.1090/S0273-0979-06-01130-X.
  88. Richeson 2012.
  89. Gibbons, Alan (1985). *Algorithmic Graph Theory*. Cambridge University Press. p. 72. ISBN 978-0-521-28881-1. Archived from the original on 20 August 2021. Retrieved 12 November 2015.
  90. Cauchy, A. L. (1813). "Recherche sur les polyèdres – premier mémoire". *Journal de l'École polytechnique* (in French). 9 (Cahier 16): 66–86. Archived from the original on 10 June 2021. Retrieved 10 June 2021.
  91. L'Huillier, S.-A.-J. (1812–1813). "Mémoire sur la polyèdrométrie". *Annales de mathématiques pures et appliquées*. 3: 169–189. Archived from the original on 10 June 2021. Retrieved 10 June 2021.
  92. Butcher, John C. (2003). *Numerical Methods for Ordinary Differential Equations*. New York: John Wiley & Sons. p. 45. ISBN 978-0-471-96758-3. Archived from the original on 19 June 2021. Retrieved 8 June 2021.
  93. Calinger 2016, pp. 96, 137.
  94. Ferraro 2008, pp. 171–180, Chapter 14: Euler's derivation of the Euler–Maclaurin summation formula.
  95. Mills, Stella (1985). "The independent derivations by Leonhard Euler and Colin Maclaurin of the Euler–Maclaurin summation formula". *Archive for History of Exact Sciences*. 33 (1–3): 1–13. doi:10.1007/BF00328047. MR 0795457. S2CID 122119093.
  96. Ojalvo, Morris (December 2007). "Three hundred years of bar theory". *Journal of Structural Engineering*. 133 (12): 1686–1689. doi:10.1061/(asce)0733-9445(2007)133:12(1686).
  97. Youschkevitch, A. P. (1971). "Euler, Leonhard". In Gillispie, Charles Coulston (ed.). *Dictionary of Scientific Biography*. Vol. 4: Richard Dedekind – Firmicus Maternus. New York: Charles Scribner's Sons. pp. 467–484. ISBN 978-0-684-16964-4.
  98. Davidson, Michael W. (February 2011). "Pioneers in Optics: Leonhard Euler and Étienne-Louis Malus". *Microscopy Today*. 19 (2): 52–54. doi:10.1017/s1551929511000046. S2CID 122853454.
  99. Calinger 1996, pp. 152–153.
  100. Home, R. W. (1988). "Leonhard Euler's 'anti-Newtonian' theory of light". *Annals of Science*. 45 (5): 521–533. doi:10.1080/00033798800200371. MR 0962700.
  101. Li, Shengcai (October 2015). "Tiny bubbles challenge giant turbines: Three Gorges puzzle". *Interface Focus*. 5 (5). Royal Society: 20150020. doi:10.1098/rsfs.2015.0020. PMC 4549846. PMID 26442144.
  102. Euler, Leonhard (1757). "Principes généraux de l'état d'équilibre d'un fluide" [General principles of the state of equilibrium of a fluid]. *Académie Royale des Sciences et des Belles-Lettres de Berlin, Mémoires* (in French). 11: 217–273. Archived from the original on 6 May 2021. Retrieved 12 June 2021. Translated into English as Frisch, Uriel (2008). "Translation of Leonhard Euler's: General Principles of the Motion of Fluids". arXiv:0802.2383 [nlin.CD].
  103. Gautschi 2008, p. 22.
  104. Baron, Margaret E. (May 1969). "A note on the historical development of logic diagrams". *The Mathematical Gazette*. 53 (383): 113–125. doi:10.2307/3614533. JSTOR 3614533. S2CID 125364002.
  105. Lemanski, Jens (2016). "Means or end? On the valuation of logic diagrams". *Logic-Philosophical Studies*. 14: 98–122.
  106. Rodgers, Peter (June 2014). "A survey of Euler diagrams" (PDF). *Journal of Visual Languages & Computing*. 25 (3): 134–155. doi:10.1016/j.jvlc.2013.08.006. S2CID 2571971. Archived (PDF) from the original on 20 August 2021. Retrieved 23 July 2021.
  107. Calinger 1996, pp. 144–145.
  108. Pesic, Peter (2014). "Euler: the mathematics of musical sadness; Euler: from sound to light". *Music and the Making of Modern Science*. MIT Press. pp. 133–160. ISBN 978-0-262-02727-4. Archived from the original on 10 June 2021. Retrieved 10 June 2021.
  109. Tegg, Thomas (1829). "Binary logarithms". *London Encyclopaedia; or, Universal Dictionary of Science, Art, Literature and Practical Mechanics: comprising a popular view of the present state of knowledge*, Volume 4. pp. 142–143. Archived from the original on 23 May 2021. Retrieved 13 June 2021.
  110. Euler 1739, p. 115.
  111. Emery, Eric (2000). *Temps et musique*. Lausanne: L'Âge d'homme. pp. 344–345.
  112. Mattheson, Johannes (1731). *Grosse General-Baß-Schule*. Vol. I. Hamburg. pp. 104–106. OCLC 30006387. Mentioned by Euler. Also: Mattheson, Johannes (1719). *Exemplarische Organisten-Probe*. Hamburg. pp. 57–59.
  113. See:
    • Perret, Wilfrid (1926). *Some Questions of Musical Theory*. Cambridge: W. Heffer & Sons. pp. 60–62. OCLC 3212114.
    • "What is an Euler-Fokker genus?". *Microtonality*. Huygens-Fokker Foundation. Archived from the original on 21 May 2015. Retrieved 12 June 2015.
  114. Euler 1739, p. 147.
  115. Euler, Leonhard (1774). "De harmoniae veris principiis per speculum musicum repraesentatis". *Novi Commentarii Academiae Scientiarum Petropolitanae*. 18. Eneström index 457: 330–353. Retrieved 12 September 2022.
  116. Gollin, Edward (2009). "Combinatorial and transformational aspects of Euler's *Speculum Musicum*". In Klouche, T.; Noll, Th. (eds.). *Mathematics and Computation in Music: First International Conference, MCM 2007 Berlin, Germany, May 18–20, 2007, Revised Selected Papers*. Communications in Computer and Information Science. Vol. 37. Springer. pp. 406–411. doi:10.1007/978-3-642-04579-0_40. ISBN 978-3-642-04578-3.
  117. Lindley, Mark; Turner-Smith, Ronald (1993). *Mathematical Models of Musical Scales: A New Approach*. Bonn: Verlag für Systematische Musikwissenschaft. pp. 234–239. ISBN 9783922626664. OCLC 27789639. See also Nolan, Catherine (2002). "Music Theory and Mathematics". In Christensen, Th. (ed.). *The Cambridge History of Western Music Theory*. New York: Cambridge University Press. pp. 278–279. ISBN 9781139053471. OCLC 828741887.
  118. Bailhache, Patrice (17 January 1997). "La Musique traduite en Mathématiques: Leonhard Euler". *Communication au colloque du Centre François Viète, "Problèmes de traduction au XVIIIe siècle"*, Nantes (in French). Archived from the original on 28 November 2015. Retrieved 12 June 2015.
  119. Euler, Leonhard (1747). *Rettung der Göttlichen Offenbahrung gegen die Einwürfe der Freygeister* [Defense of divine revelation against the objections of the freethinkers] (in German). Eneström index 92. Berlin: Ambrosius Haude and Johann Carl Spener. Archived from the original on 12 June 2021. Retrieved 12 June 2021 – via Euler Archive.
  120. Marquis de Condorcet (1805). *Comparison to the Last Edition of Euler's Letters Published by de Condorcet, with the Original Edition: A Defense of the Revelation Against the Objections of Freethinkers, by Mr. Euler Followed by Thoughts by the Author on Religion, Omitted From the Last Edition of his Letters to a Princess of Germany* (PDF). Translated by Ho, Andie. Archived (PDF) from the original on 28 April 2015. Retrieved 26 July 2021.
  121. Calinger 1996, p. 123.
  122. Calinger 1996, pp. 153–154.
  123. See:
    • Brown, B. H. (May 1942). "The Euler–Diderot anecdote". *The American Mathematical Monthly*. 49 (5): 302–303. doi:10.2307/2303096. JSTOR 2303096.
    • Gillings, R. J. (February 1954). "The so-called Euler–Diderot incident". *The American Mathematical Monthly*. 61 (2): 77–80. doi:10.2307/2307789. JSTOR 2307789.
    • Struik, Dirk J. (1967). *A Concise History of Mathematics* (3rd revised ed.). Dover Books. p. 129. ISBN 978-0-486-60255-4.
  124. Marty, Jacques (1988). "Quelques aspects des travaux de Diderot en 'mathématiques mixtes'" [Some aspects of Diderot's work in general mathematics]. *Recherches sur Diderot et sur l'Encyclopédie* (in French). 4 (1): 145–147. Archived from the original on 24 September 2015. Retrieved 20 April 2012.
  125. "Schweizerische Nationalbank (SNB) – Sechste Banknotenserie (1976)". *Swiss National Bank*. Archived from the original on 3 May 2021. Retrieved 15 June 2021.
  126. "Schweizerische Nationalbank (SNB) – Siebte Banknotenserie (1984)". *Swiss National Bank*. Archived from the original on 23 April 2021. Retrieved 15 June 2021.
  127. "E" (PDF). *Members of the American Academy of Arts & Sciences, 1780–2017*. *American Academy of Arts and Sciences*. pp. 164–179. Archived (PDF) from the original on 18 February 2019. Retrieved 17 February 2019. Entry for Euler is on p. 177.
  128. Schmadel, Lutz D., ed. (2007). "(2002) Euler". *Dictionary of Minor Planet Names*. Berlin, Heidelberg: Springer Publishing. p. 162. doi:10.1007/978-3-540-29925-7_2003. ISBN 978-3-540-29925-7.
  129. Fraser, Craig G. (11 February 2005). *Leonhard Euler's 1744 book on the calculus of variations*. Elsevier. ISBN 978-0-08-045744-4. In Grattan-Guinness 2005, pp. 168–180.
  130. Euler, Leonhard (1744). *Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti* [A method for finding curved lines enjoying properties of maximum or minimum, or solution of isoperimetric problems in the broadest accepted sense] (in Latin). Bosquet. Archived from the original on 8 June 2021. Retrieved 8 June 2021 – via Euler Archive.
  131. Reich, Karin (11 February 2005). *'Introduction' to analysis*. Elsevier. ISBN 978-0-08-045744-4. In Grattan-Guinness 2005, pp. 181–190.
  132. Ferraro, Giovanni (2007). "Euler's treatises on infinitesimal analysis: *Introductio in analysin infinitorum*, *institutiones calculi differentialis*, *institutionum calculi integralis*". In Baker, Roger (ed.). *Euler Reconsidered: Tercentenary Essays* (PDF). Heber City, UT: Kendrick Press. pp. 39–101. MR 2384378. Archived from the original (PDF) on 12 September 2022.
  133. Reviews of *Introduction to Analysis of the Infinite*:
    • Aiton, E. J. "Introduction to analysis of the infinite. Book I. Translated by John D. Blanton. (English)". zbMATH. Zbl 0657.01013.
    • Shiu, P. (December 1990). "Introduction to analysis of the infinite (Book II), by Leonard Euler (translated by John D. Blanton)". *The Mathematical Gazette*. 74 (470): 392–393. doi:10.2307/3618156. JSTOR 3618156.
    • Ştefănescu, Doru. "Euler, Leonhard *Introduction to analysis of the infinite. Book I*. Translated from the Latin and with an introduction by John D. Blanton". *Mathematical Reviews*. MR 1025504.
  134. Demidov, S. S. (2005). *Treatise on the differential calculus*. Elsevier. ISBN 978-0080457444. Archived from the original on 18 June 2021. Retrieved 12 November 2015. In Grattan-Guinness 2005, pp. 191–198.
  135. Kleinert, Andreas (2015). "Leonhardi Euleri *Opera omnia*: Editing the works and correspondence of Leonhard Euler". *Prace Komisji Historii Nauki PAU*. 14. Jagiellonian University: 13–35. doi:10.4467/23921749pkhn_pau.16.002.5258.
  136. Euler, Leonhard; Fuss, Nikola Ivanovich; Fuss, Paul (1862). *Opera postuma mathematica et physica anno 1844 detecta quae Academiae scientiarum petropolitanae obtulerunt ejusque auspicus ediderunt auctoris pronepotes Paulus Henricus Fuss et Nicolaus Fuss*. Imperatorskaia akademīia nauk (Russia). OCLC 9094558695.
  137. Calinger 2016, pp. ix–x.
  138. "The Eneström Index". *Euler Archive*. Archived from the original on 9 August 2021. Retrieved 27 May 2021.
  139. Knapp, Susan (19 February 2007). "Dartmouth students build online archive of historic mathematician". *Vox of Dartmouth*. Dartmouth College. Archived from the original on 28 May 2010.
  140. Klyve, Dominic (June–July 2011). "Euler Archive Moves To MAA Website". *MAA FOCUS*. Mathematical Association of America. Retrieved 9 January 2020.
  141. "The Euler Archive". University of the Pacific. Archived from the original on 7 June 2021.
  142. Plüss, Matthias. "Der Goethe der Mathematik". Swiss National Science Foundation. Archived from the original on 24 June 2021. Retrieved 16 June 2021.
  143. Varadarajan, V. S. (2006). *Euler through time: A new look at old themes*. American Mathematical Society. ISBN 978-0-8218-3580-7. OCLC 803144928.
  144. Libri, Gugliemo (January 1846). "Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIe siècle, ...". *Journal des Savants* (in French): 51. Archived from the original on 9 August 2018. Retrieved 7 April 2014.

来源

10. 进一步阅读

11. 外部链接

                     

© 小时科技 保留一切权利