南京理工大学 2006 量子真题
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 填空题(每题 6 分)
1.德布罗意关系为_________。
2.写出量子力学五个基本假设中的两个_________。
3.波函数的标准条件为_________。
4.能量算符表达式为_________;栋梁算符表达式为_________。
5.坐标和动量的对易关系为 $[x, p_x] = \underline{\quad\quad}$; 测不准关系是 $(\Delta x)^2 \cdot (\Delta p_x)^2 \geq \underline{\quad\quad}$。
6.对氢原子,不考虑电子的自旋,能级的简并度_________;考虑自旋但不考虑自旋与轨道角动量的耦合时,能级的简并度为_________。
7.费米子和玻色子所组成的全同粒子体系的波函数分别具有性_________和_________性。
8.原子跃迁的选择定则中角量子数应满足 $\Delta l = \underline{\quad\quad}$。磁量子数应满足 $\Delta m = \underline{\quad\quad}$。
9.考虑自旋后,波函数在自旋空间表示为 $\psi_s = \begin{pmatrix} \psi_1(x, y, z) \\ \psi_2(x, y, z) \end{pmatrix}$(已归一化),则在态 $\psi$ 下,自旋算符_________。对自旋的平均可表示为 $G = \begin{pmatrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{pmatrix}$ 对自旋的平均可表示为 $\underline{\quad\quad}$;对坐标和自旋同时求平均的结果可表示为_________。
10.算符 $\hat{Q}\text{的本征矢}|n\rangle \text{组成完备系,则}|n\rangle \text{的封闭性为} \underline{\hspace{2cm}} |n\rangle \text{在以}|x\rangle \text{为基矢的} x \text{表象中的分量}\Psi(x,t)=\underline{\hspace{2cm}}$
2. 计算题(每题 15 分)请考生在下列 7 题中任选 6 题
1. 一粒子在一维势场 $U(x)$ 中运动,求粒子的能级和对应的波函数。 $[ U(x) = \begin{cases} \infty, & x < 0 \\0, & 0 \le x \le a \\\infty, & x > a \end{cases}$
2. 氢原子处在基态 $\psi (r, \theta, \varphi) = \frac{1}{\sqrt{\pi a_0^3}} e^{-\frac{r}{a_0}}$,求在此态中:$r$ 的平均值;势能 $( -\frac{e^2}{r} )$ 的平均值;动量几率分布函数。附: $\int_0^\infty x^n e^{-\alpha x} \, dx = \frac{n!}{\alpha^{n+1}}$
3. 已知氢原子的电子波函数为 $\psi(r, \theta, \varphi, s_z) = \sqrt{\frac{1}{4}} R_{31}(r) Y_{11}(\theta, \varphi) \chi_{1/2}(s_z) + \sqrt{\frac{3}{4}} R_{32}(r) Y_{20}(\theta, \varphi) \chi_{-1/2}(s_z)$ 求在 $\psi$ 态中测量氢原子能量 $E$、$l^2$、$l_z$、$ S^2 $、$s_z$ 的可能值和这些力学量的平均值。
4. 一体系未受微扰时有三个能级 $E_1^{(0)}$, $E_2^{(0)}$, $E_3^{(0)}$, 现受一微扰 $\hat{H}'$ 作用, 在 $\hat{H}^{(0)}$ 表象中, $\hat{H} = \hat{H}^{(0)} + \hat{H}'$ 的矩阵表示为 $\begin{pmatrix}E_1^{(0)} & 0 & a \\0 & E_2^{(0)} & b \\a^* & b^* & E_3^{(0)}\end{pmatrix}$ 试用微扰论求能级至二级修正。
5. 一电子的哈密顿算符为
$\hat{H} = \frac{eB}{\mu c} \hat{S}_x$
其中 $e, B$, $\mu, c$ 为常量。
(1) 写出电子自旋 $\hat{S}_x $, $\hat{S}_y$ , $\hat{S}_z$ 在 $S_z$ 表象中的矩阵形式;并写出 $\hat{S}_x$ 的本征值和本征矢。
(2) 求电子的定态薛定谔方程的解(取 $S_x$ 表象),
(3) 若 $t = 0$ 时,电子处于 $S_z = \hbar/2$ 的本征态 $\chi(t=0) = \chi_{1/2}(S_z)$,写出 $t$ 时刻的状态 $\chi(t)$。
6. 有有均匀电场作用在电荷为 $q$ 的线性谐振子上,这个电场可以看作是微扰,它与时间的关系为 $\epsilon(t) = \frac{A}{\pi \tau^2} e^{-\left(\frac{t}{\tau}\right)^2}$, 其中 $A$ 为常数,$\tau > 0$。微扰哈密顿算符为 $\hat{H}_i = -q\epsilon(t)x$。设在加上电场之前(即 $t = \infty$),线性谐振子处于基态 $\phi_0$,求电场作用结束时(即 $t = \infty$)线性谐振子被激发到第一激发态 $\phi_1$ 的几率,准确到一级近似。附: $\int_{0}^{\infty} e^{-\alpha x^2} dx = \frac{1}{2} \sqrt{\frac{\pi}{\alpha}};$
逆推公式:$x \phi_n(x) = \sqrt{\hbar / (\mu \omega)} \left[ \sqrt{(n+1)/2} \\ \phi_{n+1}(x) + \sqrt{n/2} \\ \phi_{n-1}(x) \right]$
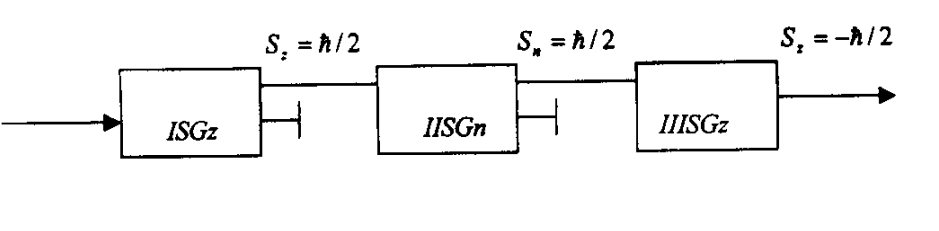
7. 一束自旋为 $1/2$ 的粒子,相继穿过三个斯特恩-革拉赫实验装置(如图三个装置分别为 $ISG_z$, $IISG_n$, $IIISG_z$)。$ISG_z$ 可使自旋 $S_z = \hbar/2$ 的粒子通过而选择 $S_z = -\hbar/2$ 的粒子。$IISG_n$ 可使自旋 $S_n = \hbar/2$ 的粒子通过而选择 $S_n = \mathbf{n} \cdot \mathbf{S} = \hbar/2$ 的粒子,$\mathbf{n}$ 为 $xz$ 平面内与 $z$ 轴成 $\theta$ 角方向的单位矢量。而 $IIISG_z$ 可使自旋 $S_z = \hbar/2$ 的粒子通过而选择 $S_z = -\hbar/2$ 的粒子。
- 求自旋算符 $S_n = \mathbf{n} \cdot \mathbf{S}$ 的本征态。
- 求穿过 $IISG_n$ 后的粒子有多大概率可以从 $IIISG_z$ 穿过。
- 如何调整 $IISG_n$ 的方向(即 $\theta$ 角)使穿过 $IIISG_z$ 的粒子数最多?