南京理工大学 普通物理 B(845)模拟五套卷 第五套
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 一、填空题 I(24 分,每空 2 分)
1.一质点沿半径为 $1m$ 的圆周运动,运动方程为 $\theta=2+3t^2$,式中 以弧度计,$t$ 以秒计,则 $t=2s$ 时,质点的切向加速度是__________,法向加速度是__________。
2. 一定滑轮质量为 $M$,半径为 $R$,对水平轴的转动惯量 $J=\frac{1}{2}MR^2$,在滑轮的边缘绕一细绳,绳的下端挂一物体,绳的质量可以忽略且不能伸长,滑轮与轴承间无摩擦,物体下落的加速度为 $a$,则绳中的张力 $T=$_________。
3. 如图所示,一静止的均匀细棒,长为 $L$,质量为 $M$,可绕通过棒的端点且垂直于棒长的光滑固定轴 $O$ 在水平面内转动,转动惯量为 $\frac{1}{3}ML^2$,一质量为 $m$、速率为 $v$ 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后 的子弹速率为 $\frac{1}{2}v$,则此时棒的角速度应为 ______________。
4. 一弹簧振子沿 $x$ 轴作简谐振动,已知振动物体最大位移为 $x_m=0.4m$,最大恢复 力为 $F_m=0.8N$,最大速度为 $v_m=0.8\pi m/s$,又知 t=0 的初位移为 $+0.2m$,且初速度与所选 $x$ 轴方向相反,则振动能量为_____________,此振动的表达式为___________。
5. 若入射波方程为 $y_1=A \cos\left(\omega t+\frac{2\pi x}{\lambda}\right) $,在 $x=0$ 处反射,若反射端为固定端,则反射波的方程为 $y_2=$_________(假设振幅不变),合成波方程为__________,波节点的位置为____________。
6. 产生动生电动势的非静电力是__________力,产生感生电动势的非静电力是________力。
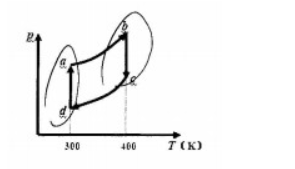
7. 以一定量的理想气体作为工作物质,在 $P-T$ 图中经图示的循环过程。图中 $a\to b$ 及 $c\to d$ 为两个绝热方程,则循环过程为__________循环,其效率为______
2. 二、填空题 II(18 分,每空 2 分)
1 单色平行光束垂直照射在宽为 $1.0mm$ 的单缝上,在缝后放一焦距为 $20m$ 的会聚透镜,已知位于透镜焦面处的屏幕上的中央明条纹宽度为 $2.5mm$,则入射光波长为_____________。
2.均匀带电的半径为 $R$ 的金属球,带电 $Q$,在距球心为 $a(a< R)$ 的一点 $P$ 处的电场强度大小 $E=$____________,电势大小 $U=$____________。
3.有一单缝,宽 $a=0.10mm$,在缝后放一焦距为 $50cm$ 的会聚透镜,用平行绿光 $(\lambda=546.0nm)$ 垂直照射单缝,则位于透明焦面处的屏幕上的中央明条纹及第二级明条纹宽_____________。
4. 两根无限长的均匀带电直线相互平行,相距为 $2a$,线电荷密度分别为 $+\lambda$ 和 $-\lambda$,则每单位长度的带电直线所受的作用力为______________。
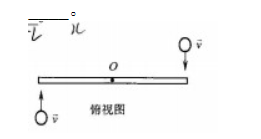
5.光滑的水平桌面上有一长为 $2L$、质量为 $m$ 的匀质细杆,可绕过其重点且垂直于杆的竖直光滑固定轴 $O$ 自由转动,其转动惯量为 $\frac{1}{3}mL^2$,起初杆静止,桌面上有两个质量均为 $m$ 的小球,各自在垂直于杆的方向上,正对着杆的一端,以相同速率 $v$ 相向运动,如图所示,当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起运动,则这一系统碰撞后的转动角速度应为 _____________。
6. $S'$ 系相对 $S$ 系以速度 $0.8c$ 沿 $X$ 轴正向运动。两参考系的原点在 $t'=t=0$ 时重合,一事件在 $S'$ 系中发生在 $x'=300 m$. $(y'=z'=0), t'=2\times10^{-7} s$,则该事件在 $S$ 系中发生的空间位置为________,时间为 _______。
7. 某一宇宙射线中 $\pi$ 介子的动能 $E_k = 7 m_0 c^2,m_0$ 为 $\pi$ 介子的静止质量, 则实验室中观察到它的寿命是它的固有寿命的 _______ 倍。
3. 三、(14 分)
一链条总长为 $l$,质量为 $m$,放在桌面上,并使其下垂,下垂一端的长度为 $a$,设链条与桌面之间的滑动摩擦系数为,令链条由静止开始运动,则:
(1)链条离开桌面的过程中,摩擦力对链条作了多少功?(2)链条离开桌面时的速率是多少?
4. 四、(14 分)
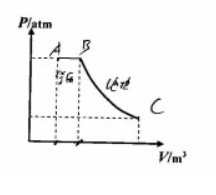
一定量的单原子分子理想气体,从 $A$ 态出发经过等压过程膨胀到 $B$ 态,又经过绝热过程膨胀到 $C$ 态,如图所示。试求这全过程中,该气体对外所做的功、内能的增量以及吸收的热量。
5. 五、(14 分)
两个半径分别为 $R_1$ 和 $R_2$ 的同心球壳,中间是空气,构成一球形电容器,设所带电量分别为 $+Q$ 和 $-Q$ 且均匀分布,求:
(1)两球壳之间的电场强度;
(2)两球壳之间的电势差;
(3)电容器的电容。
6. 六、(12 分
) 一半径为 $R$ 的均匀带电 $q$ 的介质球,介电常数为,球外为真空,求距离球心为 $r$ 处的电势。
7. 七、(14 分)
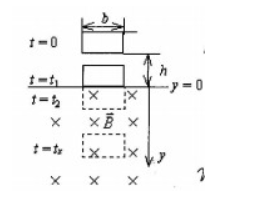
由质量为 $m$、电阻为 $R$ 的均匀导线做成的矩形线框,宽为 $b$,在 $t=0$ 时由静止下落,这时线框的下底边在 $y=0$ 平面上方高度为 $h$ 处(如图所示),$y=0$ 平面以上没有磁场;$y=0$ 平面以下则由匀强磁场 $B$,其方向在图中垂直纸面向里。现已知在时刻 $t=t_1$ 和 $t=t_2$,线框位置如图所示,求线框速度 $v$ 与时间 $t$ 的函数关系(不计空气阻力,且忽略线框自感)。
8. 八、(14 分)
有一轻弹簧,下端悬挂一质量为 $0.1kg$ 的砝码,砝码静止时,弹簧伸长 $0..05m$,如果我们再把砝码竖直拉下 $0.02m$,求放手后砝码的振动频率和振幅
9. 九、(13 分)
一玻璃劈尖的末端的厚度为 $0.05mm$,折射率为 1.50,今用波长为 $700nm$ 的平行单色光以 30°的入射角射到劈尖的上表面,试求:
(1)在玻璃劈尖的上表面所形成的干涉条纹数目;
(2)若以尺寸完全相同的由两玻璃片形成的空气劈尖代替上述的玻璃劈尖,则所产生的条纹数目又为多少?
10. 十、(13 分)
当钠黄光 $\lambda=589.3nm$ 照射某光电池时,为遏止所有电子到达阳极,需加 $0.30V$ 的反向电压。如果波长 $\lambda' =400nm$ 的光照射这个光电池,问要遏止电子, 需加多大的反向电压?