南京理工大学 普通物理 B（845）模拟五套卷 第二套

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 填空题（30 分，每空 2 分）

　　 1. 已知一质点的运动方程为 $r=\left[(5\sin2\pi t)i+(4\cos2\pi t)j\right]$（单位为米），则该质点在 $0.25s$ 末的位置是__________，从 $0.25s$ 末到 $1s$ 末的位移是___ ______。

　　 2. 一质量为 $m$ 的质点在指向圆心的平方反比力的作用下，作半径为 r 的圆 周运动，此质点的速度 $v=$__________。若取距圆心无穷远处为势能零点， 它的机械能 $E$=____________。

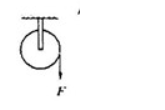
　　 3. 一轻绳绕于 $r=0.2m$ 的飞轮边缘，以恒力 $F=98N$ 拉绳，如图所示，已知 飞轮的转动惯量 $J=0.5kg\cdot m2$，轴承无摩擦。则飞轮的角加速度为______ _____；绳子拉下 $5m$ 时，飞轮的角速度为___________，动能为_______

　　 4. 已知一平面简谐波沿 $x$ 轴负向传播，振动周期 $T=0.5s$，波长 $l=10m$，振 幅 $A=0.1m$。当 $t=0$ 时波源振动的位移恰好为正的最大值。若波源处为原 点，则沿波传播方向距离波源为 $l/2$ 处的振动方程为 $y=$____________； 当 $t=T/2$ 时，$x=l/4$ 处质点的振动速度为____________。

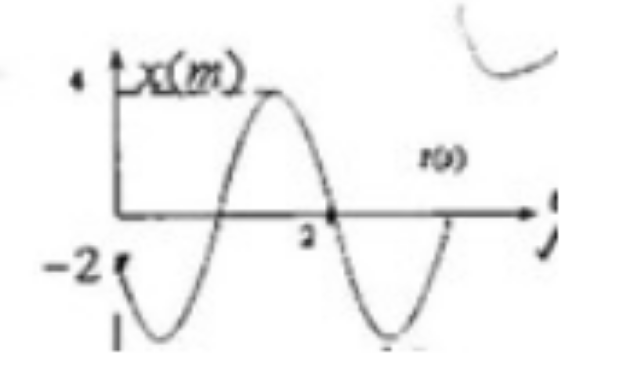
　　 5. 一 簧振子作简谐振动，其振动曲线图所示。则它的周期 $T=$________，其余弦函数描述时初相位为 _________。

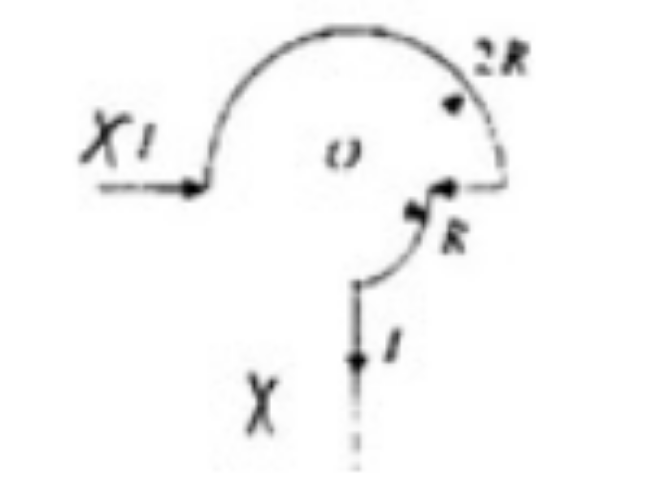
　　 6. 如图，电流在 $O$ 点的磁感应强度的大小___________，方向__________。

　　 7. 气缸内有 $2mol$ 的氦气，初始温度为 27°C，体积为 $20L$。先将氦气定压膨胀直到体积加倍，然后绝热膨胀直到恢复到初温为止，若视氦气为理想气体，则氦气的内能变化量_________，氦气所作总功为_________。

2. 填空题（16 分，每空 2 分）

　　 1. 用很薄的云母片 $(n=1.58)$ 覆盖在双缝实验中的一条缝上，这时屏幕上的零级明条纹移到原来的第七级明条纹的位置上，如果入射光波长为 $\lambda=550nm$，则问此云母片的厚度为__________。

　　 2. 若电荷以相同的面密度均匀分布在半径分别为 $r_1=10cm$ 和 $r_2=20cm$ 的两个同心球面上，设无穷远处电势为零，已知球心电势为 $300V$，则两球面的电荷面密度为__________。

　　 3. 波长为 $600nm$ 的平行光垂直照射 $12cm$ 长的两玻璃片上，两玻璃片一端相互接触，另一端夹一直径为 $d$ 的金属丝。若测得这 $12cm$ 内由 141 条明纹，则金属丝的直径为___________。

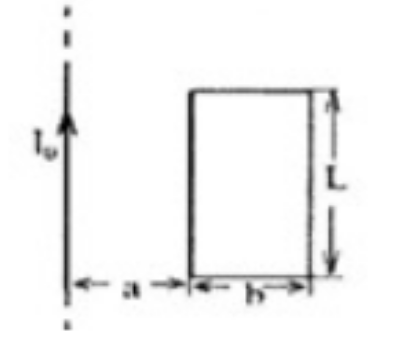
　　 4. 如图所示，一无限长直电流 $I_0$ 一侧一有其共面的矩形线圈，则通过此线圈的磁通量为____________。

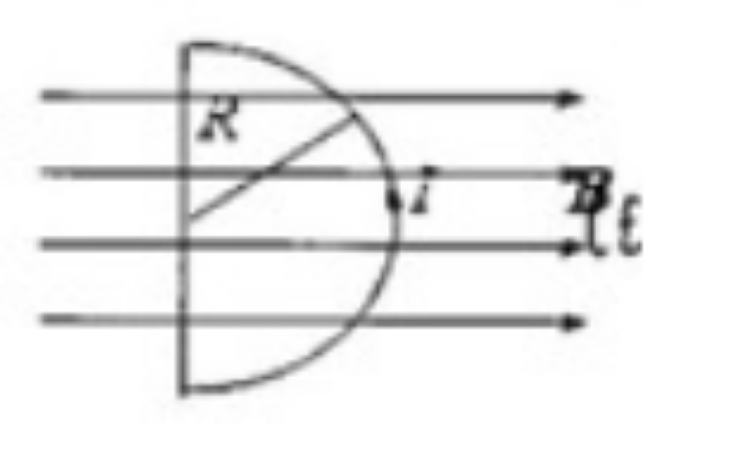
　　 5. 一半圆形闭合线圈，半径 $R=0.2m$，通过电流 $I=5A$，放在均匀磁场中，磁场方向与线圈平面平行，如图所示，磁感应强度 $B=0.5T$，则线圈所受到磁力矩为_________。若此线圈受磁力矩的作用从上述位置转到线圈平面与磁场方向成 30°的位置，则此过程中磁力矩做功为________。_______。

　　 6. 粒子在加速器中被加速到动能为静止能量的 4 倍，其质量 $m=$_______。（$m_0$ 为静止质量）

　　 7. 一体积为 $V_0$，质量为 $m_0$ 的立方体沿某一棱方向相对观察者 $A$ 以速度 $v$ 运动，则观察者 $A$ 测得密度为__________。

3. 三、（13 分）

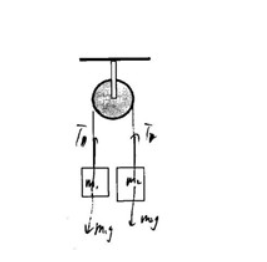
　　 一根细绳跨过一光滑的定滑轮，绳两端分别悬挂着质量为 $m1$ 和 $m2$ 的物体，$m1>m2$。求物体的加速度及绳对物体的拉力。绳与滑轮间的摩擦力可以略去不计。绳不伸长，滑轮和绳的质量也可略去不计。

4. 四、（13 分）

　　 如果一定量的理想气体，其体积和压强按照 $V=a/\sqrt{p}$ 的规律变化，其中 $a$ 为已知常数。试求：
（1）气体从体积 $V1$ 膨胀到 $V2$ 所做的功。
（2）体积为 $V1$ 时的温度 $T1$ 与体积为 $V2$ 时的温度 $T2$ 之比。

5. 五、（12 分）

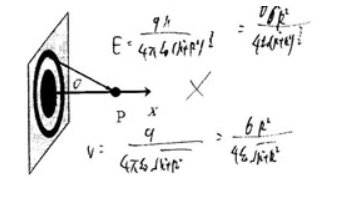
　　 一 “无限大” 平面，中部有一半径为 $R$ 的圆孔，设平面上均匀带电，电荷面密度为，式求通过小孔中心 $O$ 并与平面垂直的直线上各点的场强和电势（选 $O$ 点的电势为零）。

6. 六、（12 分）

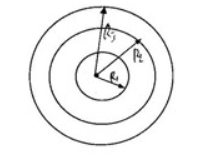
　　 一根很长的同轴电缆，由半径为 $R_1$ 的导体圆柱和套在它外面的内半径为 $R_2$，外半径为 $R_3$ 的同轴导体圆筒组成，如图所示。电流 $I$ 沿导体圆柱流去，由导体圆筒流回，设电流都均匀分布在它们的横截面上。设导体的磁导率均为 $\mu_0$。求：电缆内外磁感应强度随距轴线距离的分布。

7. 七、（14 分）

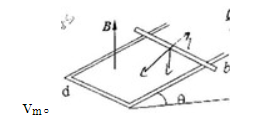
　　 一很长的长方形的 $U$ 形导轨，与水平面成角，裸导线可在导轨上无摩擦地下滑，导轨位于磁感强度 $B$ 垂直向上的均匀磁场中。设导线 $ab$ 的质量为 $m$，电阻为 $R$，长度为 l，导轨的电阻略去不计，$abcd$ 形成电流 $x=0$ 时，$v=0$。 求：（1）导线 $ab$ 下滑的速度 $v$ 与时间 $t$ 的函数关系；（2）导线 $ab$ 的最大速度

8. 八、（14 分）

　　 某质点作简谐振动，周期为 $2s$，振幅为 $0.02m$，开始计时 $(t=0)$ 时，质点恰好在负向最大位移处，求：
（1）该质点的振动方程；
（2）此振动以速度 $u=2m/s$ 沿 $x$ 轴正方向传播时，形成的一维简谐波的波 动方程；
（3）该波的波长。

9. 九、（13 分）

　　 把折射率 $n=1.4$ 的薄膜插入迈克尔逊干涉仪的一臂时，发现干涉条纹移动了 7 条，求薄膜厚度（设入射光波长 $\lambda=632.8nm$）。

10. 十、（13 分）

　　 一个电子用静电场加速后，其动能为 $0.25MeV$，求：（1）运动电子的质量； （2）电子的运动速度；（3）电子的德布罗意物质波波长。