分子轨道理论（综述）

                     

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 在化学中，分子轨道理论是一种用量子力学描述分子电子结构的方法。电子没有被分配到原子间的单个键上，而是被看作在整个分子中原子核的影响下运动的。[1] 量子力学将电子的空间和能量特性描述为分子轨道围绕分子中的两个或多个原子，并包含原子间的价电子。20 世纪初提出的分子轨道理论通过将成键电子的状态——分子轨道近似为原子轨道的线性组合(LCAO)，彻底改变了成键的研究。这些近似现在是通过将密度泛函理论(DFT)或哈特利-福克模型(Hartree–Fock models)应用于薛定谔方程而得到的。

　　 量子化学的另一个基础理论是价键理论。

1. 原子轨道的线性组合(LCAO)方法

　　 在 LCAO 方法中，每个分子都有一组分子轨道。假设分子轨道波函数 $\psi_j$ 可以写成 n 个原子轨道 $\chi_i$ 的简单加权和，如下式所示：[2]

　　 $\psi_j = \sum_{i=1}^{n} c_{ij} \chi_i$

　　 可以通过将该方程代入薛定谔方程并应用变分原理来确定 cij 系数的数值。变分原理是量子力学中用来建立每个原子轨道基系数的一种数学方法。较大的系数意味着轨道基由更多的有特定贡献的原子轨道组成——因此，分子轨道最适合用这种类型来表征。这种将轨道贡献量化为原子轨道线性组合的方法在计算化学中得到了应用。在某些计算方案中，可以在系统上应用额外的酉变换来加速收敛。在 20 世纪 30 年代，分子轨道理论被认为是价键理论的竞争对手，后来人们才认识到这两种方法是密切相关的，并且在延伸后，它们是等价的。

2. 历史

　　 分子轨道理论是在价键理论建立(1927 年)的几年后发展起来的，主要贡献者是弗里德里希·洪特、罗伯特·穆利肯、约翰·斯莱特和约翰·伦纳德·琼斯。[3] 分子轨道理论最初被称为洪德-穆利肯理论。[4] 根据德国物理学家和物理化学家埃里希·休克尔的说法，分子轨道理论的第一次定量应用是在 1929 年伦纳德·琼斯的论文中。[5][6] 这篇论文在价键理论之前预测并解释了双氧分子的三重基态的顺磁性[7] (见分子轨道图§双氧)，价键理论在 1931 年对此进行了解释。[8] 轨道这个词是穆利肯在 1932 年提出的。[4] 到 1933 年，分子轨道理论已经被公认是一个有效和有用的理论。[9]

　　 埃里希·休克尔从 1931 年开始将分子轨道理论应用于不饱和烃分子，用他的胡克尔分子轨道(HMO)方法测定π电子的分子轨道能量，并将其应用于共轭烃和芳烃。[10][11] 该方法解释了苯等六π电子分子的稳定性。

　　 1938 年，查尔斯·库尔森首次对氢分子轨道波函数进行了精确计算。[12] 到 1950 年，分子轨道完全被定义为自洽场哈密顿量的本征函数(波函数)，此时分子轨道理论才变得完全严格和一致。[13] 这种严格的方法被称为分子的哈特利-福克(Hartree-Fock)方法，尽管它起源于对原子的计算。在分子的计算中，分子轨道以原子轨道基组的形式展开，从而得到 Roothaan 方程。[14] 这导致了许多量子化学从头计算方法的发展。与此同时，在现在被称为半经验量子化学方法中使用一些经验推导出的参数，以更近似的方式应用分子轨道理论。[14]

　　 分子轨道理论的成功也催生了配体场理论，配体场理论是在 20 世纪 30 年代和 40 年代作为晶体场理论的替代而发展起来的。

3. 轨道类型

图
图 1：分子轨道图显示了从两个 H 原子的原子轨道形成 H2（中心）的分子轨道。较低能量的分子轨道是成键轨道，电子密度集中在两个 H 核之间。较高能量的分子轨道是反键轨道，电子密度集中在每个 H 核的后面。

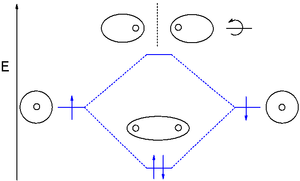
　　 分子轨道理论使用原子轨道(LCAO)的线性组合来表示原子间键产生的分子轨道。这些通常分为三种类型，成键轨道、反键轨道和非成键轨道。成键轨道将电子密度集中在给定的一对原子之间的区域，因此它的电子密度往往会使两个原子核相互吸引，并使两个原子结合在一起。[15] 反键轨道将电子密度集中在每个核的 “后面”(即每个原子离另一个原子最远的一侧)，因此往往会使两个原子核相互排斥，实际上削弱了两个核之间的键。非成键轨道中的电子往往与原子轨道相关联，而原子轨道之间不存在正或负的相互作用，这些轨道中的电子既不会增加键的强度，也不会减弱键的强度。[15]

　　 分子轨道根据它们形成的原子轨道的类型被进一步划分。如果化学物质的轨道相互作用时能量变低，它们就会形成成键相互作用。不同的成键轨道因电子构型(电子云形状)和能级的不同而不同。

　　 分子的分子轨道可以用分子轨道图来描述。

4. 概观

　　 分子轨道理论为化学键提供了一个全局的、非局域的视角。在分子运动理论中，分子中的任何电子都可以在分子中的任何地方找到，因为量子条件允许电子在任意数量原子核的影响下运动，只要它们处于某些量子规则允许的本征态。因此，当通过高频光或其他方式得到所需量的能量激发时，电子可以跃迁到高能量的分子轨道上。例如，在氢双原子分子的简单情况下，单个电子从成键轨道到反键轨道的跃迁可以在紫外辐射下发生。这种跃迁作用削弱了两个氢原子之间的键，并可能导致光解离——由于光的吸收而导致化学键的断裂。

　　 尽管在分子轨道理论中，一些分子轨道可能包含了在特定分子原子对之间的电子，但另一些轨道可能包含在分子上分布更均匀的电子。但总的来说，在分子轨道理论中键的离域性要大得多，这使得它比价键理论更适用于具有等效非整数键序的共振分子。这使得分子轨道理论在描述拓展系统的时候更加有用。

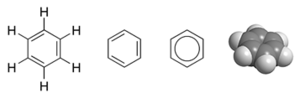
　　 一个例子是苯的分子轨道描述 $C_6H_6$。它是一个六个碳原子和三个双键组成的芳族六边形环。在这个分子中，30 个总价电子中的 24 个来自碳原子，6 个来自氢原子—位于 $12\sigma$ 成键轨道中，这些电子主要位于成对原子（碳-碳或碳-氢）之间，类似于价键理论中描述的电子。然而，剩余的六个成键电子位于三个 $\pi$ 成键分子轨道中，这些轨道是在环周围离域的。这六个电子，有两个电子在一个分子轨道中，对所有六个原子的轨道贡献相等。其他四个电子轨道相互垂直重叠。根据 VB 理论，这六个离域电子都存在于环平面之上和之下的更大空间中。苯中所有的碳碳键在化学上是等价的。在分子轨道理论中，这是三个分子轨道结合，并在六个碳原子上均匀分布额外六个电子的直接结果。

图
图 2：苯的结构

　　 在甲烷分子中，$CH_4$，分布在所有五个原子上的四个分子轨道中有八个价电子。然而，可以将四个分子轨道转换成四个定域 $sp^3$ 轨道。莱纳斯·鲍林(Linus Pauling)在 1931 年杂化了碳的 2s 和 2p 轨道，使它们直接指向氢 1s 的基函数并具有最大重叠。然而，离域分子轨道描述更适合用于预测电离能和光谱吸收带的位置。甲烷电离时，从价电子分子轨道中取出一个电子，它可以来自 s 键或三重简并 p 键能级，产生两个电离能。相比之下，VB 理论的解释更加复杂。当从 $sp^3$ 轨道移除一个电子时，在四个价键结构之间引起共振，每个价键结构有一个单电子键和三个双电子键。三重简并 $T_2$ 和 $A_1$ 电离态($CH4^+$)由这四种结构的不同线性组合产生。电离态和基态之间的能量差产生了两种电离能。

　　 像苯一样，在β胡萝卜素、叶绿素或血红素等物质中，π轨道中的一些电子在分子轨道中长距离分布，导致较低能量(可见光谱)的光吸收，产生了这些物质的特征颜色。[16] 分子的许多光谱数据在分子轨道理论中得到了很好的解释，重点是与多中心轨道相关的电子态，包括基于轨道对称匹配原理的轨道混合。[15] 同样，分子轨道原理也自然地解释了一些电学现象，例如石墨中存在的六边形原子片在平面方向上的高电导率。这是由于半填充 p 轨道的连续带重叠造成的，并解释了石墨的导电现象。分子轨道理论认为，石墨原子层中的一些电子在任意距离上都是完全离域的，并且存在于覆盖整个石墨层的非常大的分子轨道中，因此一些电子可以自由移动，从而在层平面中导电，就像它们存在于金属中一样。

5. 参考文献

  1. Daintith, J. (2004). Oxford Dictionary of Chemistry. New York: Oxford University Press. ISBN 978-0-19-860918-6..
  2. Licker, Mark, J. (2004). McGraw-Hill Concise Encyclopedia of Chemistry. New York: McGraw-Hill. ISBN 978-0-07-143953-4.CS1 maint: Multiple names: authors list (link).
  3. Coulson, Charles, A. (1952). Valence. Oxford at the Clarendon Press..
  4. Mulliken, Robert S. (1972) [1966]. "Spectroscopy, Molecular Orbitals, and Chemical Bonding" (pdf) (Press release). Nobel Lectures, Chemistry 1963–1970. Amsterdam: Elsevier Publishing Company..
  5. Hückel, Erich (1934). "Theory of free radicals of organic chemistry". Trans. Faraday Soc. 30: 40–52. doi:10.1039/TF9343000040..
  6. Lennard-Jones, J.E. (1929). "The electronic structure of some diatomic molecules". Trans. Faraday Soc. 25: 668–686. doi:10.1039/TF9292500668..
  7. Coulson, C.A. Valence (2nd ed., Oxford University Press 1961), p.103.
  8. Pauling, Linus (1931). "The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond". J. Am. Chem. Soc. 53 (9): 3225–3237. doi:10.1021/ja01360a004..
  9. Hall, George G (1991). Lennard-Jones Paper of 1929 "Foundations of Molecular Orbital Theory" Check |url= value (help). Advances in Quantum Chemistry. 22: 1–6. Bibcode:1991AdQC...22....1H. doi:10.1016/S0065-3276(08)60361-5. ISBN 978-0-12-034822-0. ISSN 0065-3276..
  10. E. Hückel, Zeitschrift für Physik, 70, 204 (1931); 72, 310 (1931); 76, 628 (1932); 83, 632 (1933)..
  11. Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978..
  12. Coulson, C.A. (1938), "Self-consistent field for molecular hydrogen", Mathematical Proceedings of the Cambridge Philosophical Society, 34 (2): 204–212, Bibcode:1938PCPS...34..204C, doi:10.1017/S0305004100020089.
  13. Hall, G.G. (7 August 1950). "The Molecular Orbital Theory of Chemical Valency. VI. Properties of Equivalent Orbitals" (pdf). Proc. Roy. Soc. A. 202 (1070): 336–344. Bibcode:1950RSPSA.202..336H. doi:10.1098/rspa.1950.0104..
  14. Jensen, Frank (1999). Introduction to Computational Chemistry. John Wiley and Sons. ISBN 978-0-471-98425-2.. vMiessler and Tarr (2013), Inorganic Chemistry, 5th ed, 117-165, 475-534..
  15. Griffith, J.S. and L.E. Orgel. "Ligand Field Theory". Q. Rev. Chem. Soc. 1957, 11, 381-383.

                     

© 小时科技 保留一切权利