莫雷拉定理（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

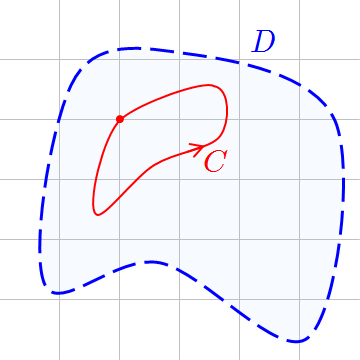
　　 在复分析中，莫雷拉定理（Morera's theorem，以贾钦托·莫雷拉 Giacinto Morera 命名）给出了一个判断函数是否为全纯函数的判据。设 $f$ 是定义在复平面开集 $D$ 上的连续复值函数，如果它对 $D$ 中的每一条分段 $C^1$ 的闭曲线 $\gamma$ 都满足 $$ \oint_{\gamma} f(z)\,dz = 0,~ $$ 那么 $f$ 必定在 $D$ 上是全纯函数。这个条件等价于 $f$ 在 $D$ 上存在一个原函数（反导函数）。不过该定理的逆命题一般并不成立：一个全纯函数并不一定在其定义域上都有原函数，除非附加额外条件。如果定义域 $D$ 是单连通的，那么逆命题成立，这正是柯西积分定理的内容，即全纯函数沿闭合曲线的积分为零。

　　 一个典型的反例是函数 $f(z) = 1/z$，它在 $\mathbf{C} - \{0\}$ 上是全纯的。在 $\mathbf{C} - \{0\}$ 中任意一个单连通邻域 $U$ 上，$1/z$ 都有一个原函数，可以写为 $L(z) = \ln\left(r\right) + i\theta, \quad z = re^{i\theta}$. 由于 $\theta$ 的取值可以相差任意整数倍的 $2\pi$，所以在区域 $U$ 中，只要能连续地选取 $\theta$ 的分支，就可以在该 $U$ 上定义出 $1/z$ 的一个原函数。（无法在包含原点的闭合曲线上连续地定义 $\theta$，正是 $1/z$ 在整个定义域 $\mathbf{C} - \{0\}$ 上没有原函数的根本原因。）此外，由于常数的导数为 0，原函数中加上任意常数仍然是 $1/z$ 的一个原函数。

　　 从某种意义上说，$1/z$ 这个反例具有普遍性：对于任何在其定义域上没有原函数的解析函数，其根本原因都可以追溯到 $1/z$ 在 $\mathbf{C} - \{0\}$ 上没有原函数这一事实。

1. 证明

图
图 1：如果沿任意闭合曲线 $C$ 的积分都为零，那么函数 $f$ 在区域 $D$ 上是全纯的。
图
图 2：从点 $a$ 到点 $b$ 的两条路径上的积分是相等的，因为它们的差值等于沿一条闭合回路的积分。

　　 该定理有一个相对初等的证明方法，即通过显式构造一个 $f$ 的原函数来完成。

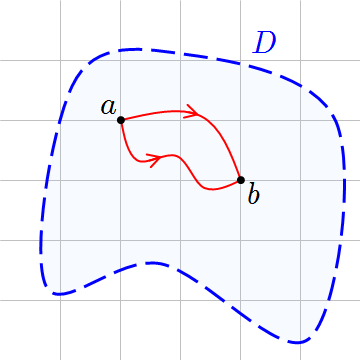
　　 不失一般性，假设区域 $D$ 是连通的。选定 $D$ 中的一个点 $z_0$，对任意 $z \in D$，令 $\gamma: [0,1] \to D$ 是一条分段 $C^1$ 的曲线，满足 $\gamma(0) = z_0, \quad \gamma(1) = z$.定义函数 $$ F(z) = \int_{\gamma} f(\zeta)\,d\zeta~ $$ 为了说明这个定义是良好的，假设有另一条分段 $C^1$ 曲线 $\tau: [0,1] \to D$，同样满足 $\tau(0) = z_0, \quad \tau(1) = z$.考虑曲线 $\gamma \tau^{-1}$（即先沿着 $\gamma$ 然后反向沿着 $\tau$ 的组合曲线），它是一条闭合的分段 $C^1$ 曲线。于是有 $$ \int_{\gamma} f(\zeta)\,d\zeta + \int_{\tau^{-1}} f(\zeta)\,d\zeta = \oint_{\gamma \tau^{-1}} f(\zeta)\,d\zeta = 0~ $$ 由此可得 $$ \int_{\gamma} f(\zeta)\,d\zeta = \int_{\tau} f(\zeta)\,d\zeta~ $$ 证明了 $F(z)$ 的定义与所选路径无关。利用 $f$ 的连续性估计差商，可以得出 $ F'(z) = f(z)$.如果选择不同的 $z_0$，函数 $F$ 只会相差一个常数，即在新旧 $z_0$ 之间沿任意分段光滑曲线积分 $f$ 的结果，但这不会改变导数。

　　 由于 $f$ 是全纯函数 $F$ 的导数，因此 $f$ 也是全纯的。全纯函数的导数仍然全纯，可以通过以下事实来证明：全纯函数是解析的，即可以表示为收敛幂级数，而幂级数可以逐项求导。这就完成了证明。

2. 应用

　　 莫雷拉定理是复分析中的标准工具，几乎所有涉及以非代数方式构造全纯函数的论证中都会用到它。

一致收敛

　　 例如，假设 $f_1, f_2, \dots$ 是一列全纯函数，它们在某个开圆盘上一致收敛于一个连续函数 $f$。根据柯西定理，对于圆盘内的任意闭合曲线 $C$，都有 $$ \oint_{C} f_n(z)\,dz = 0~ $$ 对每个 $n$ 都成立。由于一致收敛，可以得到 $$ \oint_{C} f(z)\,dz = \oint_{C} \lim_{n \to \infty} f_n(z)\,dz = \lim_{n \to \infty} \oint_{C} f_n(z)\,dz = 0~ $$ 对任意闭合曲线 $C$ 都成立。由莫雷拉定理可知，$f$ 必然是全纯的。这个结论还可以用来证明，对于任意开集 $\Omega \subseteq \mathbf{C}$，所有有界解析函数 $u: \Omega \to \mathbf{C}$ 组成的集合 $A(\Omega)$，在取上确界范数的意义下是一个巴拿赫空间。

无穷和与积分

　　 莫雷拉定理还可以结合 Fubini 定理和 Weierstrass M-检验，用于证明由无穷和或积分定义的函数是解析的，例如黎曼 $\zeta$ 函数 $$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}~ $$ 或 Gamma 函数 $$ \Gamma(\alpha) = \int_0^{\infty} x^{\alpha - 1} e^{-x} \, dx~ $$ 具体来说，可以通过写成 $$ \oint_C \Gamma(\alpha) \, d\alpha = \oint_C \int_0^{\infty} x^{\alpha - 1} e^{-x} \, dx \, d\alpha~ $$ 来处理合适闭曲线 $C$ 上的积分，然后利用 Fubini 定理交换积分次序，得到 $$ \int_0^{\infty} \oint_C x^{\alpha - 1} e^{-x} \, d\alpha \, dx = \int_0^{\infty} e^{-x} \oint_C x^{\alpha - 1} \, d\alpha \, dx~ $$ 由于映射 $\alpha \mapsto x^{\alpha - 1}$ 是解析的，有 $$ \oint_C x^{\alpha - 1} \, d\alpha = 0~ $$ 因此上式的双重积分为 0。

　　 类似地，在处理 $\zeta$ 函数的情形下，利用 M-检验可以证明在闭曲线上的积分与无穷求和可以互换，从而证明 $\zeta$ 函数在适当区域内的解析性。

3. 假设的弱化

　　 莫雷拉定理中的假设条件可以大幅放宽。特别是，只要区域 $D$ 中的任意一个闭合（实心）三角形 $T$ 都满足 $$ \oint_{\partial T} f(z)\,dz = 0~ $$ 那么这个条件就足以刻画全纯性：即 $f$ 在 $D$ 上全纯，当且仅当上述条件成立。这一结果还带来了前述 “全纯函数一致收敛极限仍然全纯” 结论的推广：如果 $f_1, f_2, \dots$ 是定义在开集 $\Omega \subseteq \mathbb{C}$ 上的一列全纯函数，并且在 $\Omega$ 的每一个紧子集上一致收敛于某个函数 $f$，那么 $f$ 也是全纯的。

4. 参见

5. 参考文献

6. 外部链接

                     

© 保留一切权利