马尔可夫链蒙特卡洛

贡献者： lrqlrqlrq

　　 马尔可夫链蒙特卡洛（Markov Chain Monte Carlo，简称 MCMC）是一种用于从概率分布中抽样的统计方法。这种方法结合了马尔可夫链和蒙特卡洛模拟的思想，被广泛应用于贝叶斯统计、统计物理学、天文学、机器学习等领域。

1. 动机

贝叶斯推断 Bayesian Inference

　　贝叶斯推断的主要目标是通过结合先验分布和观测数据，利用贝叶斯定理推导参数的后验分布。在观测到数据 $D$ 后，更新我们对参数 $\theta$ 的信念。这一过程通过贝叶斯定理实现，其中先验概率分布 $P(\theta)$ 表达了我们在看到数据之前对参数的信念，似然函数 $P(D|\theta)$ 表达了在给定参数情况下观测到实际数据的可能性，而后验概率分布 $P(\theta|D)$ 则是我们在看到数据后对参数的更新信念。该定理建立了先验概率 $P(\theta)$、似然函数 $P(D|\theta)$ 和得到的后验概率 $P(\theta|D)$ 之间的关系。

\begin{equation} P(\theta|D) = \frac{P(D|\theta) \times P(\theta)}{P(D)} = \frac{P(D|\theta) \times P(\theta)}{\int P(D|\hat{\theta}) \times P(\hat{\theta}) \, d\hat{\theta}}~. \end{equation}

　　然而，在计算分母中的证据 $P(D)$ 时可能具有挑战性，特别是在涉及高维空间或复杂的多峰模型的情况下。这种计算需要在整个参数空间上进行积分，这可能非常耗费资源。因此，当面临没有解析解或共轭先验不可用的情况时，使用蒙特卡洛积分等数值积分方法变得至关重要。

蒙特卡罗积分 Monte Carlo Integration

　　蒙特卡罗积分是一种通过随机抽样来估计复杂积分的数值近似方法。均值估计法包括通过随机抽样在定义域内生成大量均匀分布的随机点。随后，它计算这些随机点对应的函数值的平均值，并乘以定义域的总体积，以得到函数积分的估计值。对于利用均值估计方法计算 $I = \int_a^b h(x) \,dx$，其中 $X \sim \text{D}(a,b)$，

\begin{align} E [h(X)] =& \ \frac{1}{b-a} \int_a^b h(x) \ dx = \frac{I}{b-a}~. \end{align}

　　考虑到 $\{ X_i\} \ \text{i.i.d.} \sim \text{D}(a,b), \ i=1,\ldots,N $，使得 $Y_i = h(X_i)$ 表示一组独立同分布的随机变量，大数定律使我们能够推断：

\begin{align} \frac{1}{N} \sum_{i=1}^N h(X_i) & \to E [h(X)] = \frac{I}{b-a}, \ (N \to \infty)\\ \tilde I &= \frac{b-a}{N} \sum_{i=1}^N h(X_i)~. \end{align}

　　该方法的误差可以使用中心极限定理确定：

\begin{align} \sqrt{N}(\tilde I - I) \stackrel{\mbox{d}}{\longrightarrow} N\big(0, (b-a)^2 \ \text{Var}(h(X)) \big)~.\end{align}

因此，我们得到 $\tilde I - I = O(1/\sqrt{N})$，这意味着每增加一位小数的精度计算，所需的样本数需要增加 $100$ 倍。

　　该方法的实现非常直接简单。例如，要使用 $1000$ 个样本计算 $I = E [|X|^{3/2}]$，给定 $X \sim N(0,1)$，只需一行 Python 代码即可完成：

np.mean(np.abs(np.random.normal(size=1000)) ** 1.5)

然而，显而易见的是，我们认为这种方法简单是因为在 numpy 中有针对正态分布的内置随机抽样函数。但实际上，从分布中抽样存在相当大的复杂性并遇到许多挑战。这种复杂性凸显了我们即将介绍的抽样方法。

抽样方法 Sampling Method

　　 逆变换抽样 Inverse transform sampling 利用累积分布函数（CDF）依赖于从均匀分布中抽取的随机数来产生符合期望概率分布的随机变量。

　　本质上，给定累积分布函数 $\Phi(X) $，如果 $ Y \sim \text{Uniform}(0, 1) $，使用逆变换 $ X = \Phi^{-1}(Y) $ 将产生一个随机变量 $ X $，它符合概率分布 $\Phi(x)$，其中 $ \Phi^{-1} $ 表示 $\Phi$ 的逆函数。为了表明 $Y$ 在 $[0, 1]$ 上均匀分布，我们需要证明对于任意 $0 \leq u \leq 1$，$P(Y \leq u) = u$。

\begin{align} P(Y \leq u) &= P(\Phi(X) \leq u) \\ &= P(X \leq \Phi^{-1}(u)) \quad \text{(使用 } \Phi \text{ 的逆函数)} \\ &= \Phi(\Phi^{-1}(u)) \quad \text{(根据 CDF 的定义)} \\ &= u ~. \end{align}

　　然而，这种方法存在显著的局限性。计算概率密度函数的积分通常是非常困难的，这也是我们需要使用蒙特卡洛积分方法的原因。此外，需要注意的是 $ \Phi(x) $ 可能没有逆函数。

　　 拒绝抽样 Rejection sampling 通过使用简单的提议分布生成样本，根据接受或拒绝的标准保留符合目标分布的样本。考虑到生成概率密度函数 $f(x)$ 的样本的目标，令 $g(x)$ 表示一个易于抽样的已知分布，并假设存在一个常数 $M$，使得对所有 $x$，都有 $M \cdot g(x) \geq f(x)$。

　　该过程从提议分布 $g(x)$ 中抽取样本 $x$ 开始，随后从区间 $[0, M \cdot g(x)]$ 中选择一个随机数 $u$。如果 $u \leq f(x)$，则接受样本 $x$；否则拒绝样本，并重新开始抽样过程。通过这个迭代过程，最终获得符合目标分布 $f(x)$ 的一组随机样本。重要的是，拒绝抽样的有效性取决于选择一个适当的提议分布 $g(x)$，该分布紧密围绕目标分布，并最小化被拒绝的样本数量，从而提高抽样效率。

　　 重要性抽样 Importance sampling 为了计算 $I = \int_\Omega h(x) \,dx$，在域 $\Omega$ 内 $h(x)$ 值的变异性可能很大，导致采用直接的均值估计方法会导致许多样本点聚集在零附近。因此，可以通过非均匀抽样的方法进行改进：在 $|h(x)|$ 较大的地方密集分配点，在 $|h(x)|$ 较小的地方稀疏分布点。令 $g(x)$ 与 $|h(x)|$ 的形状相似，当 $g(x) = 0$ 时，$h(x) = 0$，且当 $|x| \to \infty$ 时，$h(x)$ 行为类似于 $o$-阶无穷小相比于 $g(x)$。令 $ X_i \ \text{i.i.d.} \sim g(x), \ i=1,\ldots,N $，使得 $\eta_i = h(X_i)/g(X_i)$，因此，

\begin{align} E[\eta] = \int_\Omega \frac{h(x)}{g(x)} g(x) \,d x = \int_\Omega h( x) \,d x = I~. \end{align}

　　因此，$\{\eta_i\}$ 的样本均值可用于估计 $I$，即，

\begin{align} \hat I = \frac{1}{N} \sum_{i=1}^N \frac{h(X_i)}{g(X_i)}~. \end{align}

重要性抽样的核心在于将积分 $I$ 重新定义为期望，

\begin{align} I &= \int h(x) f(x) \, dx = \mathbb{E}_{f}[h(X)]\\ I &= \int h(x) \frac{f(x)}{g(x)} g(x) \, dx = \mathbb{E}_{g}\left[\frac{h(X)f(X)}{g(X)}\right]~. \end{align}

表达式 $\frac{h(X)f(X)}{g(X)}$ 包含了重要性抽样权重。积分 $I$ 可以使用以下方式估计，

\begin{align} \hat I = \frac{1}{N} \sum_{i=1}^{N} \frac{h(x_i)f(x_i)}{g(x_i)}~. \end{align}

然而，当重要性分布 $g(x)$ 在 $h(x)$ 对积分贡献较大的区域与 $f(x)$ 显著偏离时，估计器可能表现出较高的方差，导致不准确性。

　　因此，我们希望确定一个最优的重要性分布 $g(x)$ 来最小化方差或增强收敛性。理论上，以方差为标准的最优重要性分布具有以下形式：

\begin{align} g^{*}(x)=\frac{|h(x)|f(x)}{\int|h(s)f(s)d s|}~. \end{align}

最优重要性的证明：

\begin{align} \text{Var}\left[\frac{f(x)h(x)}{g^{*}(x)}\right]&=\int\frac{h(x)^{2}f(x)^{2}}{g^{*}(x)}d x+\left(\int h(x) f(x)\right)^{2} \\ \text{Var}\left[\frac{f(x)h(x)}{g^{*}(x)}\right]&-\left(\int h(x) f(x)\right)^{2}=\int\frac{h(x)^{2}f(x)^{2}}{\frac{|h(x)|f(x)}{\int|h(x)f(x)dx|}}d x \\ &=\int|h(x)f(x)d x|\int|h(x)|f(x)d x\\ &=\left(\frac{\int|h(x)|f(x)}{g(x)} g(x) d x\right)^2\\ &\leq \frac{\int h(x)^2f(x)^2}{g(x)^2} g(x) d x \text{, Cauchy Schwarz inequality }\\ &=\int\frac{h(x)^{2}f(x)^{2}}{g(x)}d x\\~. \end{align}

　　这个结果在实践中并不十分实用，因为我们首先不知道 $\int h(x) f(x)$，大多数情况下我们需要找到 $\int|h(x)f(x)dx|$。此外，在分布密度 $h(x)$ 是多峰的情况下，很难确定一个合适的 $g(x)$。

高维局限性

　　在拒绝抽样中的接受概率由以下公式确定：

\begin{align} p(\text{接受}) &= \int\frac{f(x)}{M \ g(x)} \ g(x) \ d x \\ &=\frac{1}{M}\int f(x) \ d x~. \end{align}

　　考虑分布 $f(x) \sim N(0, I)$ 和 $g(x)\sim N(0, \sigma^2 I)$，注意 $\sigma \geq 1$ 以确保 $g(x)$ 足够涵盖 $f(x)$，记得 $f(x) \leq Mg(x)$，在 $d$ 维空间中有，

\begin{align} g(0) = \frac{1}{(\sqrt{2\pi}\sigma)^d}, \ \ f(0) = \frac{1}{(2\pi)^{d/2}}~. \end{align}

因此，常数 $M$ 需要满足，

\begin{align} M \geq \frac{f(0)}{g(0)} = \frac{(\sqrt{2\pi}\sigma)^d}{(2\pi)^{d/2}} = \sigma^d~. \end{align}

因此，当 $d \to \infty$ 时，$p(\text{接受})\to 0$。在高维场景中，拒绝抽样的接受率显著降低。因此，在 $N$ 个样本中，找到一个落在 $f(x)$ 内的点变得极为困难。以下是一个使用拒绝抽样计算超球体体积的 Python 代码，使用了 $10000$ 个样本。偶尔在第 $13$ 维时失败，无法找到落在超球体内的点。

def hypersphere_volume(dimensions, samples):
    count_inside = 0
    for _ in range(samples):
        point = np.random.uniform(low=-1, high=1, size=dimensions)
        if np.linalg.norm(point) <= 1:
            count_inside += 1
    volume = (count_inside / samples) * (2 ** dimensions)
    return volume
print('dim = n estimated volume = '+ str(hypersphere_volume(n, 10000)))
dim = 3 estimated volume = 4.1568,   dim = 13 estimated volume = 0.0

2. 马尔可夫链蒙特卡洛 (MCMC)

　　 MCMC 是一种高维随机抽样方法，解决了先前的抽样方法在处理高维和复杂分布时的困难。该方法模拟了一个马尔可夫链，使马尔可夫链的稳定分布成为目标分布，从而生成大量大致符合目标分布的样本，但这些样本彼此之间并不独立。

马尔可夫链 Markov Chain

　　随机过程 $\{X_t, t=0, 1, \dots \}$ 在有限状态空间 $S=\{1,2, \dots,m\}$ 中运行，其中 $X_t\in S$ 表示时间 $t$ 系统的状态。如果 $\{X_t\}$ 遵循仅依赖于其前一状态的概率转移，表示为，

\begin{align} & P(X_{t+1} = j | X_0=k_0, \dots X_{t-1}=k_{t-1}, X_t=i) \nonumber\\ =& P(X_{t+1} = j | X_t=i) = p_{ij}, \quad t=0,1,\dots, \ k_0, \dots, k_{t-1}, \ i, j \in S~. \end{align}

　　那么 $\{X_t\}$ 构成一个马尔可夫链，其中 $p_{ij}$ 表示转移概率。值得注意的是，$\sum_{j=1}^m p_{ij}=1$。转移概率矩阵 $P = (p_{ij})_{m\times m}$ 记录了系统中任意两个状态之间的转移可能性。

　　以下是一个 Python 代码示例，展示了状态转移矩阵对初始状态的影响。此外，在 $t_{30}$ 处不同的初始概率分布最终收敛到相同的稳定概率分布。

transfer_matrix = np.array([[0.5, 0.3, 0.2], [0.2, 0.5, 0.3],
                                             [0.1, 0.2, 0.7]])
start_matrixs = [np.array([[0.7, 0.1, 0.2]]), np.array([[0.4, 0.2, 0.4]])]
for start_matrix in start_matrixs:
  values = [[] for _ in range(start_matrix.shape[1])]
  num_iterations = 30
  for i in range(num_iterations):
      start_matrix = np.dot(start_matrix, transfer_matrix)
      for j in range(start_matrix.shape[1]):
          values[j].append(start_matrix[0][j])

　　然后，本文将从数学角度进行探讨。对于任意的 $i,j\in S$，其中 $i \neq j$，如果存在 $k\geq 1$ 使得 $p_{ij}^k > 0$，则 $\{X_t\}$ 是一个不可约链 (irreducible chain)。在这样的链中，所有状态都是相互连接的，在多个步骤后可以进行状态之间的转移。如果 $\{X_t\}$ 中的状态 $i$ 被称为 非周期性 aperiodic，如果存在 $k\geq 0$ 使得 $p_{ii}^{(k)} > 0$ 并且 $p_{ii}^{(k+1) } > 0$。如果一个马尔可夫链的所有状态都具有这个特性，则称其为非周期性。如果不可约马尔可夫链中的一个状态是非周期性，则该链中的所有状态都是非周期性。

　　对于具有有限状态空间的非周期性不可约马尔可夫链，存在以下极限：

\begin{align} \lim_{n\to\infty} P(X_n = j | X_0=i) = \pi_j~. \end{align}

在这里，$\{\pi_j\}$ 表示 $\{X_t\}$ 的极限分布。要使 $\{\pi_j\}$ 成为极限分布，必须满足 $\sum_{j=1}^m \pi_j=1$。如果在具有有限状态空间的非周期性不可约马尔可夫链中，极限分布和稳态分布是存在且相等的。这种等价性来源于方程：

\begin{equation} P(X_{t+1}=j)=\sum_{i=1}^{m}P(X_{t}=i)P(X_{t+1}=j|X_ {t}=i)=\sum_{i=1}^{m}P(X_{t}=i)p_{i j}~. \end{equation}

　　对两边取极限，可得到关系式 $\sum_{i=1}^m \pi_i p_{ij} = \pi_j$。

　　 为什么在蒙特卡洛积分中我们可以模拟一个马尔科夫链来进行采样？该马尔科夫链需要满足那些性质？在马尔可夫链中，状态的性质包括常返和正常返。

　　状态 $i$ 若从该状态出发总能再次返回，则称其为常返。对于常返状态 $i$，若从 $i$ 出发首次返回 $i$ 的时间的期望是有限的，则称其为正常返。在不可约的马尔可夫链中，只要存在正常返状态，所有状态都是正常返的。此时，存在唯一的平稳分布 $\pi$。

　　对于非周期且正常返的不可约马尔可夫链，它具有极限分布，即当 $n$ 趋向于无穷时，状态转移概率矩阵的 $n$ 次幂趋近于平稳分布 $\pi$：

\begin{align} \lim_{n\to\infty} p_{ij}^{(n)} = \pi_j, \ \forall i, j \in S ~. \end{align}

　　假设不可约马尔可夫链的平稳分布为 $\pi$，并且 $h$ 是状态空间 $S$ 上的有界函数，那么当模拟马尔可夫链并从某个初始分布出发时，函数 $h$ 关于马尔可夫链样本路径的平均值将趋近于 $\sum_{x \in S} \pi_x h(x)$：

\begin{align} P\left( \lim_{n\to\infty} \frac{1}{n} \sum_{k=0}^n h(X_k) = \sum_{x \in S} \pi_x h(x) \right) = 1~. \end{align}

　　这类似于独立同分布随机变量平均值的强大数律。当马尔可夫链按照平稳分布 $\pi$ 的转移概率模拟时，上述极限等同于 $E[h(Y)]$，其中 $Y$ 服从平稳分布 $\pi$。

　　因此，可以通过设计满足不可约、非周期、正常返性质的马尔可夫链，并使用其模拟平稳分布 $\pi$，从而估计关于 $Y \sim \pi$ 的随机变量的函数期望 $E[h(Y)]$。

　　 如何得到有平稳分布的转移概率矩阵？

　　一个充分条件是转移概率满足细致平衡条件。如果存在 $\{ \pi_j, j \in S \}, \ \pi_j\geq 0, \ \sum_{j\in S} \pi_j = 1$，使得：

\begin{align} \pi_i p_{ij} = \pi_j p_{ji}, \ \forall i \neq j ~. \end{align}

　　那么这些马尔可夫链被称为满足细致平衡条件，如果 $P(X_{t+1} = j) = \pi_i$，那么

\begin{align} P(X_{t+1} = j) = \sum_i \pi_i p_{ij} = \sum_i \pi_j p_{ji} = \pi_j \sum_i p_{ji} = \pi_j, \ \forall j \in S. ~. \end{align}

　　因此 $\{\pi_j\}$ 是 $\{X_t\}$ 的稳态分布。

3. 马尔可夫链抽样算法

　　通过马尔可夫链抽样进行蒙特卡洛模拟，需要具有稳态分布样本的转移概率矩阵。然而，通常情况下，目标稳态分布 $\{\pi_j\}$ 和状态转移矩阵 $P$ 不满足详细平衡条件：

\begin{align} \pi_i p_{ij} \neq \pi_j p_{ji}, \ \forall i \neq j ~. \end{align}

　　令 $\alpha$ 表示接受概率，使得：

\begin{align} \pi_i p_{ij}\alpha(i, j) = \pi_j p_{ji} \alpha(j, i), \ \forall i \neq j ~. \end{align}

　　因此，如果 $\alpha(i, j) = \pi_j p_{ji}$ 且 $\alpha(j, i) = \pi_j p_{ij}$，则可以获得满足详细平衡条件的转移矩阵 $P_d = P \alpha(i,j)$。然而，在这个抽样算法中，$\alpha(i, j)$ 的值可能会非常小，导致拒绝的样本值较多，并且抽样效率大幅降低。

Metropolis–Hastings 算法

　　 Metropolis–Hastings 算法通过将 $\alpha(i, j)$ 缩放到 $ C\alpha(i, j) = 1$ 来解决抽样接受率低的问题。因此，可以定义：

\begin{equation} \alpha(i, j) = \min \left\{ 1, \frac{\pi(j)P(j, i)}{\pi(i)P(i, j)} \right\}~. \end{equation}

　　这种调整加速了收敛速度。假设随机变量 $X$ 服从分布 $\pi(x), x\in \mathcal{X}$。该算法需要一个提议转移概率函数 $T(y, x),\ x,y \in \mathcal {X}$，满足 $0 \leq T(y, x) \leq 1$，$\sum_y T(y, x) = 1$，且 $ T(y, x)>0 \Leftrightarrow T(x, y) >0 $。

　　从 $\mathcal{X}$ 中选择任意初始值 $X^0$。在当前状态 $X^t$ 经过 $t$ 步之后，下一步涉及从提议转移分布 $T(y, X^t)$ 中提取 $Y$ 并生成 $u\sim U (0,1)$。随后是非常关键的步骤：

　　随后的关键步骤是基于以下规则更新 $X^{t+1}$：

\begin{align} X^{(t+1)} = \begin{cases} Y & \text{若 } u \leq \alpha(X^{(t)}, Y) \\ X^{(t)} & \text{其他情况} \end{cases} ~. \end{align}

　　 证明：MH 抽样的转移概率 $A(x,y) = P(X^{(t+1)} = y | X^{(t)} = x)$ 满足详细平衡条件。当 $x\neq y$ 时，我们有

\begin{align} \pi(x) A(x,y) =& \pi(x) T(y , x) \min \left\{ 1, \frac{\pi(y)T(x , y)}{\pi(x)T(y , x)} \right\}\\ =& \min \left\{ \pi(x)T(y , x), \pi(y)T(x , y) \right\}\\ =&\pi(y) T(x, y) \min \left\{ 1, \frac{\pi(x)T(y , x)}{\pi(y)T(x, y)} \right\}\\ =& \pi(y) A(y,x)~. \end{align}

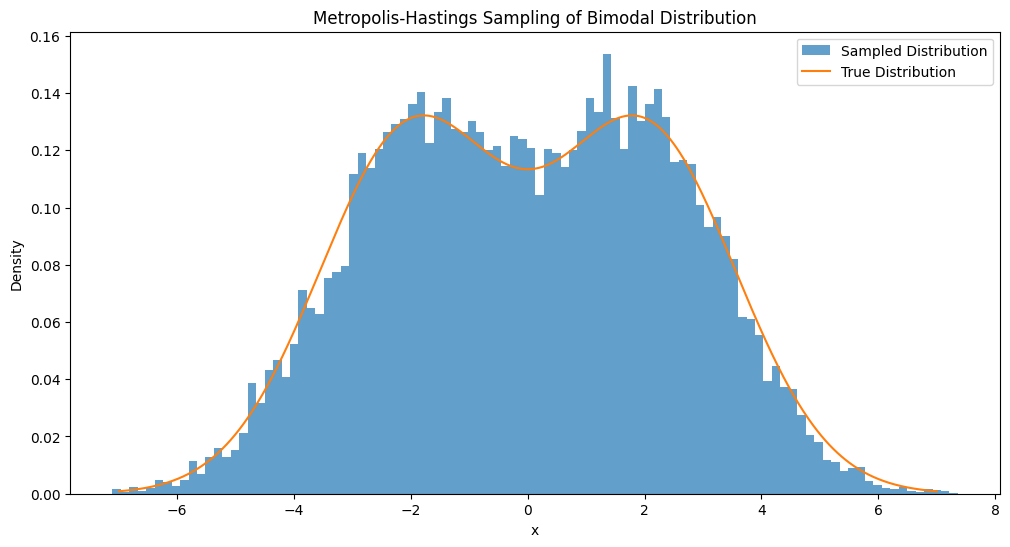
　　下面的 Python 代码演示了 MH 算法的实现，包括示例和绘制双峰分布的抽样图。这个例子双峰比较靠近彼此，实际上若是双峰分开的比较远，那么有时该算法就不能很好的进行抽样，也就是抽样集中在一个峰上而忽略了另一个，这时就需要我们选择一个方差大的提议分布。

from scipy.integrate import quad
def target_distribution(x):
    return 0.5 * np.exp(-0.2 * (x + 2)**2) + 0.5 * np.exp(-0.2 * (x - 2)**2)
def normalized_target_distribution(x):
    normalization_factor, _ = quad(target_distribution, -np.inf, np.inf)
    return target_distribution(x) / normalization_factor
def gaussian_proposal(current_state, std_dev=1.0):
    return np.random.normal(current_state, std_dev)
def metropolis_hastings_sampling(target, proposal, 
                                num_samples, initial_state=0):
    samples = [initial_state]
    current_state = initial_state
    for i in range(num_samples):
        proposed_state = proposal(current_state)
        acceptance_ratio = min(1, 
                    target(proposed_state) / target(current_state))
        if np.random.rand() < acceptance_ratio:
            current_state = proposed_state
        samples.append(current_state)
    return samples
    
num_samples = 20000
samples = metropolis_hastings_sampling(target_distribution, 
    gaussian_proposal, num_samples)

plt.hist(samples, bins=100, density=True,
         alpha=0.7, label='Sampled Distribution')
x = np.linspace(-7, 7, 1000)
plt.plot(x, normalized_target_distribution(x),
        label='True Distribution')

图 1：Metropolis-Hastings Sampling of Bimodal Distribution

Gibbs 采样

　　 MH 采样方法包括多个步骤，尝试从先前状态转移到新状态。随后，根据样本提议与目标分布的接近程度接受或拒绝提议样本。拒绝导致保留先前状态，从而增强了效率。相比之下，Gibbs 采样仅致力于沿着坐标轴移动，并利用当前点的条件分布确定后续的试验抽样分布。该方法接受所有试验样本，无需拒绝，从而可能提高效率。具体而言，在 Gibbs 采样中，指定 $T(y, x)$ 确保了 $A(x,y) = 1$ 的恒定真值，促进了加速收敛和抽样率。

　　 Gibbs 采样器通过在每个步骤中仅抽样一个变量（坐标轴）来更新完整的变量集，并利用条件分布从联合分布中抽样。在数学上，假设一个多维概率分布 $p(x_1, x_2, ..., x_n)$，Gibbs 采样算法的操作如下：首先，从当前状态 $(x_1^{(t)}, x_2^{(t)}, ..., x_n^{(t)})$ 中随机选择一个变量 $x_i$。随后，基于其他变量的当前值，从条件概率分布 $p(x_i | x_1^{(t)}, x_2^{(t)}, ..., x_{i-1}^{(t)}, x_{i+1}^{( t)}, ..., x_n^{(t)})$ 中提取新值 $x_i^{(t+1)}$。这个迭代过程持续进行，直到满足收敛条件的样本被获得。

　　 Gibbs 采样通过在每个步骤中基于条件概率进行迭代抽样，逐渐使样本序列朝向目标分布收敛。类似于前述解释，证明 Gibbs 采样满足详细平衡条件涉及考虑 $\boldsymbol x = (x_1, x_2, \dots, x_n)$ 和选择 $x_i$ 的概率作为 $q(i)$。如果 $\boldsymbol x$ 和 $\boldsymbol y$ 仅在恰好一个变量 $x_i$ 的状态上不同，其中 $y_j = x_j$ 对于 $j\neq i$，$y_i\neq x_i$，则有：

\begin{align} \pi(\boldsymbol x) A(\boldsymbol x,\boldsymbol y) =& \pi(\boldsymbol x ) q(i) p(y_i, \boldsymbol x_{j\neq i})\\ =& p(x_i, \boldsymbol x_{j\neq i})q(i)\frac{p(y_i, \boldsymbol x_{j\neq i})}{p(\boldsymbol x_{j\neq i})}\\ =&p(y_i, \boldsymbol x_{j\neq i})q(i)\frac{p(x_i, \boldsymbol x_{j\neq i})}{p(\boldsymbol x_{j\neq i})}\\ =& \pi(\boldsymbol y ) q(i) p(x_i, \boldsymbol x_{j\neq i}) = \pi(\boldsymbol x) A(\boldsymbol y,\boldsymbol x) ~. \end{align}

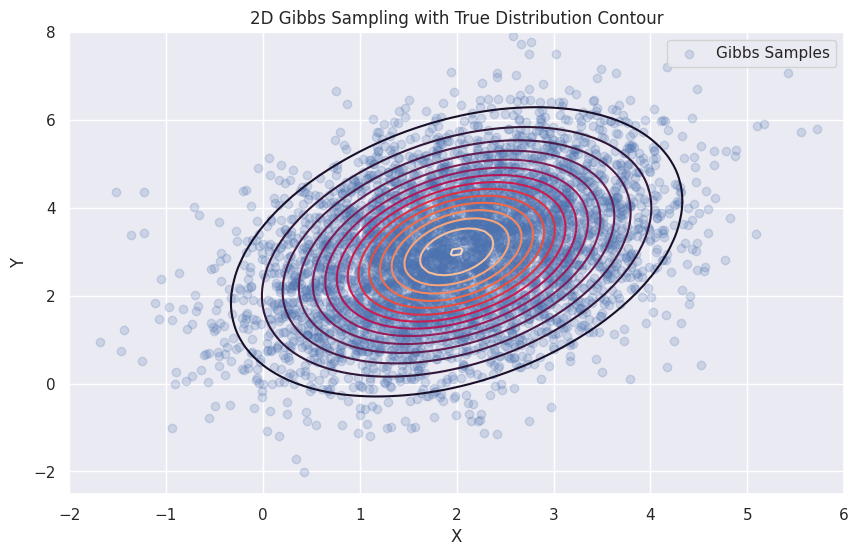
　　以下 Python 代码演示了 Gibbs 算法的实现，包括用于对二维正态分布进行抽样的示例和绘图：

图 2：2D Gibbs Sampling with True Distribution Contour

from scipy.stats import multivariate_normal

mean = [2, 3]
cov = [[1, 0.5], [0.5, 2]]
rv = multivariate_normal(mean, cov)

def gibbs_sampling(num_samples, init=(0, 0)):
    samples = np.zeros((num_samples, 2))
    samples[0] = init
    for i in range(1, num_samples):
        x = samples[i - 1, 0]
        y = samples[i - 1, 1]
        x = np.random.normal(mean[0] + cov[0][1] * 
        (y - mean[1]) / cov[1][1], 
        np.sqrt(cov[0][0] - (cov[0][1] ** 2) / cov[1][1]))
        y = np.random.normal(mean[1] + 
        cov[0][1] * (x - mean[0]) / cov[0][0],
        np.sqrt(cov[1][1] - (cov[0][1] ** 2) / cov[0][0]))
        samples[i] = [x, y]
    return samples

num_samples = 5000
samples = gibbs_sampling(num_samples)

x = np.linspace(-2, 6, 100)
y = np.linspace(-2, 8, 100)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
Z = rv.pdf(pos)

plt.figure(figsize=(10, 6))
plt.contour(X, Y, Z, levels=15)
plt.scatter(samples[:, 0], samples[:, 1], alpha=0.2, label='Gibbs Samples')