洛伦兹群（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在物理学和数学中，洛伦兹群是指闵可夫斯基时空上的所有洛伦兹变换所构成的群。闵可夫斯基时空是所有（非引力）物理现象的经典与量子背景。洛伦兹群的名字来源于荷兰物理学家亨德里克·洛伦兹。

　　 例如，以下定律、方程和理论都遵循洛伦兹对称性：

　　 洛伦兹群体现了自然界所有已知基本规律中时空的基本对称性。在时空区域足够小、引力差异可以忽略的情况下，物理规律与狭义相对论一样，保持洛伦兹不变性。

1. 基本性质

　　 洛伦兹群是庞加莱群（即闵可夫斯基时空所有等距变换所成的群）的一个子群。洛伦兹变换严格来说就是那些保持原点不变的等距变换。因此，洛伦兹群是闵可夫斯基时空等距群关于原点的各向同性子群。出于这个原因，洛伦兹群有时被称为齐次洛伦兹群，而庞加莱群则被称为非齐次洛伦兹群。洛伦兹变换是线性变换的一个例子；而闵可夫斯基时空的一般等距变换则是仿射变换。

物理学定义

图
图 1：亨德里克·安东·洛伦兹（Hendrik Antoon Lorentz, 1853–1928），洛伦兹群即以他的名字命名。

　　 假设有两个惯性参考系 $(t, x, y, z)$ 与 $(t', x', y', z')$，以及两个点 $P_1, P_2$。洛伦兹群是所有在这两个参考系之间的变换集合，这些变换保持光在两点之间传播的速度不变： \[ c^{2}(\Delta t')^{2}-(\Delta x')^{2}-(\Delta y')^{2}-(\Delta z')^{2} = c^{2}(\Delta t)^{2}-(\Delta x)^{2}-(\Delta y)^{2}-(\Delta z)^{2}.~ \] 用矩阵形式表示，这些变换是所有满足下式的线性变换 $\Lambda$： \[ \Lambda^{\mathsf{T}} \eta \Lambda = \eta, \qquad \eta = \operatorname{diag}(1,-1,-1,-1).~ \]

数学定义

　　 在数学上，洛伦兹群可以描述为不定正交群 $O(1,3)$，即保持如下二次型的不变的矩阵李群： \[ (t,x,y,z)\;\mapsto\; t^{2}-x^{2}-y^{2}-z^{2}~ \] 作用在 $\mathbb{R}^4$ 上（赋予这一二次型的向量空间有时记作 $\mathbb{R}^{1,3}$）。当写成矩阵形式时（参见经典正交群），这一二次型在物理学中被解释为闵可夫斯基时空的度规张量。

符号说明

　　 在表示洛伦兹群时，$O(1,3)$ 与 $O(3,1)$ 两种记号都被广泛使用。前者指保持一个符号型为 $(+,-,-,-)$ 的度规的矩阵，后者则对应符号型为 $(-,+,+,+)$ 的度规。由于度规整体符号在定义方程中无关紧要，因此这两类矩阵群是相同的。

　　 在当代，有部分领域倾向采用 $(1,3)$ 的记号，而 $(3,1)$ 的记号在现今实践和历史文献中依然大量存在。本文所描述的一切内容，对 $O(3,1)$ 的记号同样成立，只需作相应的符号替换。类似的考虑同样适用于相关定义（例如 $SO^{+}(1,3)$ 与 $SO^{+}(3,1)$）。

数学性质

　　 洛伦兹群是一个六维的、非紧致的、非阿贝尔的实李群，并且它不是连通的。其四个连通分支都不是单连通的。\(^\text{[1]}\) 洛伦兹群的单位元所在的连通分支本身构成一个群，通常称为受限洛伦兹群，记作 $SO^{+}(1,3)$。受限洛伦兹群由那些同时保持空间取向与时间方向的洛伦兹变换组成。其基本群的阶为 2，而它的普适覆盖群——不定自旋群 $Spin(1,3)$——同构于特殊线性群 $SL(2,\mathbf{C})$ 和辛群 $Sp(2,\mathbf{C})$。这些同构使得洛伦兹群可以作用于大量对物理学非常重要的数学结构，最典型的就是旋量。因此，在相对论性量子力学和量子场论中，通常把 $SL(2,\mathbf{C})$ 称作洛伦兹群，并理解为 $SO^{+}(1,3)$ 是它的一个特定表示（即矢量表示）。

　　 洛伦兹群在闵可夫斯基空间上的一种常见表示使用了双四元数，它们构成一个合成代数。洛伦兹变换的等距性来源于这种合成性质： \[ |pq| = |p| \times |q|.~ \] 洛伦兹群的另一性质是共形性，即角度保持。洛伦兹推动作用为时空平面上的双曲旋转，而这种 “旋转” 保持双曲角，即相对论中使用的快度的度量。因此，洛伦兹群是时空共形群的一个子群。

　　 需要注意的是，本文称 $O(1,3)$ 为 “洛伦兹群”，$SO(1,3)$ 为 “正规洛伦兹群”，而 $SO^{+}(1,3)$ 为 “受限洛伦兹群”。许多作者（尤其在物理学中）使用 “Lorentz group” 一词指代 $SO(1,3)$（甚至有时是 $SO^{+}(1,3)$）而不是 $O(1,3)$。在阅读此类文献时，需要明确辨清他们所指的具体是哪一个群。

连通分支

图
图 2：二维空间加一个时间维度中的光锥

　　 因为洛伦兹群 $O(1,3)$ 是一个李群，所以它既是一个群，同时也可以在拓扑学上描述为一个光滑流形。作为流形，它有四个连通分支。直观上，这意味着它由四个在拓扑上彼此分离的部分组成。

　　 这四个连通分支可以通过其元素的两类变换性质来分类：

　　 保持时间方向的洛伦兹变换称为正时。正时变换的子群通常记作 $O^{+}(1,3)$。保持空间取向的称为正规变换，作为线性变换，它们的行列式为 $+1$。（而非正规洛伦兹变换的行列式为 $-1$。）正规洛伦兹变换的子群记作 $SO(1,3)$。\(^\text{[a]}\)

　　 保持空间取向与时间方向的所有洛伦兹变换所构成的子群称为正规正时洛伦兹群，或称为受限洛伦兹群，记作 $SO^{+}(1,3)$。

　　 这四个连通分支的集合可以通过商群 $O(1,3)\,/\,SO^{+}(1,3)$ 赋予群结构，该商群同构于克莱因四元群。$O(1,3)$ 中的任意元素都可以表示为一个正规正时变换与离散群元素的半直积： \[ \{1,\, P,\, T,\, PT\},~ \] 其中 $P$ 和 $T$ 分别是宇称与时间反演算子： \[ P = \operatorname{diag}(1,-1,-1,-1), \quad T = \operatorname{diag}(-1,1,1,1).~ \] 因此，一个任意的洛伦兹变换可以由一个正规正时洛伦兹变换，加上两个额外的比特信息来唯一确定，这两个比特信息决定了四个连通分支中的哪一个。这一模式是有限维李群的典型特征。

2. 受限洛伦兹群

　　 受限洛伦兹群 $SO^{+}(1,3)$ 是洛伦兹群的单位元分支，这意味着它包含了所有可以通过一条连续曲线与单位元相连的洛伦兹变换。受限洛伦兹群是完整洛伦兹群的一个连通正规子群，并且具有相同的维数，在此情形下为六维。

　　 受限洛伦兹群由普通的空间旋转和洛伦兹推动生成（洛伦兹推动是包含类时方向的双曲空间中的 “旋转”\(^\text{[2]}\)）。由于每一个正规正时洛伦兹变换都可以写作一次旋转（由三个实参数指定）与一次推动（也由三个实参数指定）的乘积，因此需要六个实参数来唯一确定一个任意的正规正时洛伦兹变换。这也是理解受限洛伦兹群为何是六维的一种方式。（另见洛伦兹群的李代数。）

　　 所有旋转构成的集合形成一个李子群，与普通旋转群 $SO(3)$ 同构。而所有推动构成的集合并不构成子群，因为两个推动相乘一般并不再是一个推动。（相反，两个非共线推动等价于一次推动加一次旋转，这与托马斯旋转相关。）沿某个方向的推动，或绕某个轴的旋转，生成一个一参数子群。

传递性曲面

图
图 3

　　 如果一个群 $G$ 作用在空间 $V$ 上，那么一个曲面 $S \subset V$ 称为传递性曲面，如果 $S$ 在 $G$ 下是不变的（即 $\forall g \in G,\, \forall s \in S:\, gs \in S$），并且对于任意两点 $s_{1}, s_{2} \in S$，存在某个 $g \in G$ 使得 $g s_{1} = s_{2}$。

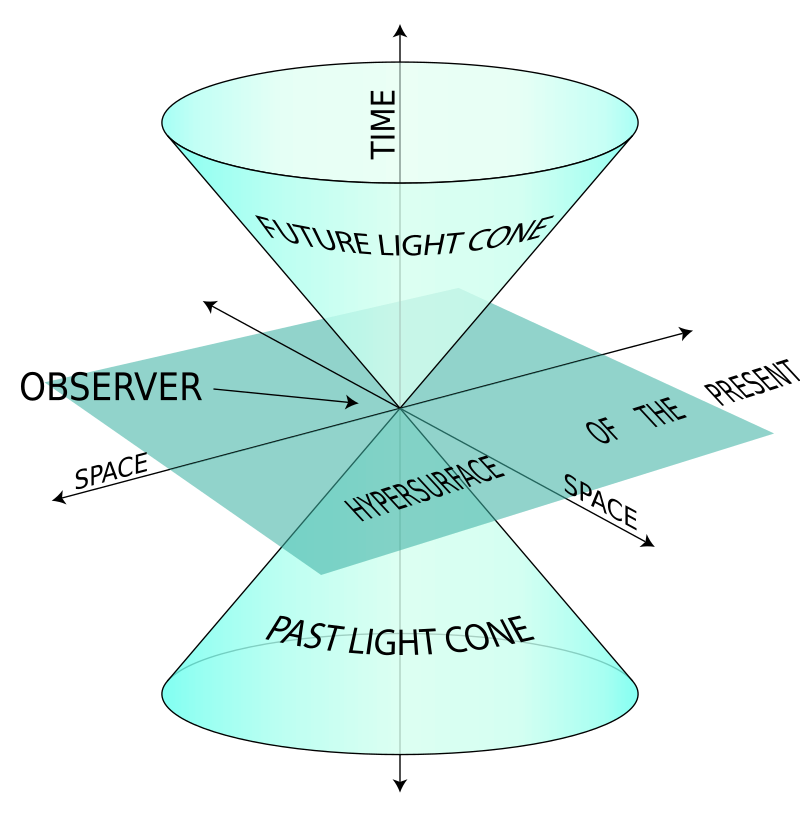
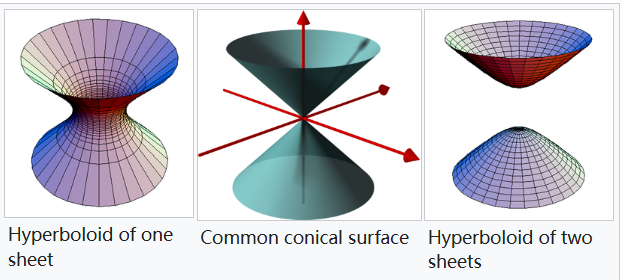
　　 根据洛伦兹群的定义，它保持如下二次型： \[ Q(x) = x_{0}^{2} - x_{1}^{2} - x_{2}^{2} - x_{3}^{2}.~ \] 在平直时空 $\mathbf{R}^{1,3}$ 上，正时洛伦兹群 $O^{+}(1,3)$ 的传递性曲面 $Q(x)=\text{const.}$ 如下所示：\(^\text{[3]}\)

　　 这些曲面都是三维的，因此相应的图像并不完全忠实，但对于 $O^{+}(1,2)$ 的对应情形则是忠实的。对于完整的洛伦兹群而言，传递性曲面只有四类，因为变换 $T$ 会将双曲面（或光锥）的上支映射到下支，反之亦然。

　　 对称空间的视角

　　 对上述传递性曲面的另一种等价表述方式是将其看作李理论意义下的对称空间。例如，根据轨道–稳定子定理，双叶双曲面的上支可以写作商空间 $SO^{+}(1,3) \,/\, SO(3)$.此外，这一上支还可以作为三维双曲空间的一个模型。

洛伦兹群的表示

　　 这些观察为寻找洛伦兹群、事实上是庞加莱群的所有无限维酉表示提供了一个良好的起点，所使用的方法是诱导表示\(^\text{[4]}\)。 具体做法是：首先在每一个传递性曲面上选取一个 “标准向量”，然后考察哪些子群保持这些向量。物理学家称这些子群为小群。问题于是基本上被化简为寻找小群的表示这一相对容易的问题。例如，在某个双叶双曲面上，可以恰当地选取一个标准向量为 $(m,\, 0,\, 0,\, 0)$. 对于每一个 $m \neq 0$，该向量恰好位于双曲面的一支。在这种情况下，小群就是旋转群 $SO(3)$，而它的所有表示都是已知的。粒子在何种精确的无限维酉表示下变换，是其分类的一部分。并不是所有的表示都能对应到物理粒子（就目前所知而言）。单叶双曲面上的标准向量对应于快子；光锥上的对应于光子，以及更具假设性的引力子；而与原点对应的 “粒子” 则是真空。

3. 同态与同构

　　 有若干其他群与受限洛伦兹群 $SO^{+}(1,3)$ 同态或同构。这些同态在解释物理学中的各种现象时发挥了关键作用。

外尔表象

　　 外尔表象，或称为旋量映射，是从 $SL(2,\mathbb{C})$ 到 $SO^{+}(1,3)$ 的一对满同态。它们在宇称变换下形成一对匹配对，分别对应于左、右手手性旋量。

　　 可以通过如下方式定义 $SL(2,\mathbb{C})$ 在闵可夫斯基时空上的作用：将时空中的一点表示为一个 $2\times 2$ 厄米矩阵，形式为 \[ \overline{X} = \begin{bmatrix} ct+z & x - i y \\ x + i y & ct - z \end{bmatrix} = ct\,1\!\!1 + x\sigma_{x} + y\sigma_{y} + z\sigma_{z} = ct\,1\!\!1 + \vec{x}\cdot\vec{\sigma},~ \] 其中 $\sigma_{x}, \sigma_{y}, \sigma_{z}$ 是泡利矩阵。

　　 这种表述，即外尔表象，满足 \[ \det \overline{X} = (ct)^{2} - x^{2} - y^{2} - z^{2}.~ \] 因此，可以将厄米矩阵的空间（作为实向量空间是四维的）与闵可夫斯基时空对应起来，使得一个厄米矩阵的行列式正好等于闵可夫斯基时空中相应向量的平方长度。一个元素 $S \in SL(2,\mathbb{C})$ 在厄米矩阵空间上的作用为 \[ \overline{X} \;\mapsto\; S \,\overline{X}\, S^{\dagger},~ \] 其中 $S^{\dagger}$ 是 $S$ 的厄米共轭转置。此作用保持行列式不变，因此 $SL(2,\mathbb{C})$ 通过（线性）等距变换作用于闵可夫斯基时空。

　　 其宇称反演形式为 \[ X = ct\,1\!\!1 - \vec{x}\cdot\vec{\sigma},~ \] 其变换规律为 \[ X \;\mapsto\; \bigl(S^{-1}\bigr)^{\dagger}\, X \, S^{-1}.~ \] 该变换是正确的，可以通过以下事实加以验证： \[ \overline{X}\,X = \left(c^{2}t^{2} - \vec{x}\cdot \vec{x}\right)1\!\!1 = \left(c^{2}t^{2} - x^{2} - y^{2} - z^{2}\right)1\!\!1,~ \] 在上述一对变换下保持不变。

　　 这些映射都是满射，其核都是二元子群 $\{\pm I\}$。根据第一同构定理，商群 $PSL(2,\mathbf{C}) = SL(2,\mathbf{C}) / \{\pm I\}$ 同构于 $SO^{+}(1,3)$。

　　 宇称映射交换这两个覆盖，它对应于厄米共轭是 $SL(2,\mathbf{C})$ 的一个自同构。这两个不同的覆盖对应于洛伦兹群在旋量上的两种不同的手性作用。无上划线的形式对应于右手旋量的变换：$\psi_{R} \;\mapsto\; S \psi_{R}$,而带上划线的形式对应于左手旋量的变换：$\psi_{L} \;\mapsto\; (S^{\dagger})^{-1}\,\psi_{L}$.

　　 需要注意的是，这一对覆盖在量子化之后不再保持；当进行量子化时，这会导致一种特殊的现象，即手征反常。洛伦兹群的经典对称性（即非量子化时的对称性）在量子化过程中被破坏；这正是 Atiyah–Singer 指数定理的内容。

符号约定

　　 在物理学中，通常用 $\Lambda \in SO^{+}(1,3)$ 表示一个洛伦兹变换，并写作 ${\Lambda^{\mu}}_{\nu}$,从而显式展示带有时空指标 $\mu,\nu = 0,1,2,3$ 的矩阵。

　　 一个四矢量可以通过泡利矩阵以两种方式构造： \[ \sigma^{\mu} = (I,\, \vec{\sigma}), \qquad \overline{\sigma}^{\mu} = (I,\, -\vec{\sigma}).~ \] 这两种形式通过宇称变换相联系。需要注意的是，$\overline{\sigma}_{\mu} = \sigma^{\mu}$.给定一个洛伦兹变换 $x^{\mu} \;\mapsto\; x^{\prime \mu} = {\Lambda^{\mu}}_{\nu}\, x^{\nu}$,上文所给的由 $S \in SL(2,\mathbf{C})$ 对正时洛伦兹群的二重覆盖可以写作 \[ x^{\prime \mu}\,\overline{\sigma}_{\mu} = \overline{\sigma}_{\mu}\,{\Lambda^{\mu}}_{\nu}\,x^{\nu} = S \, x^{\nu}\,\overline{\sigma}_{\nu}\, S^{\dagger}.~ \] 去掉 $x^{\mu}$ 后，这一关系可以写作 \[ \overline{\sigma}_{\mu}\,{\Lambda^{\mu}}_{\nu} = S \,\overline{\sigma}_{\nu}\, S^{\dagger}.~ \] 其宇称共轭形式为 \[ \sigma_{\mu}\,{\Lambda^{\mu}}_{\nu} = \left(S^{-1}\right)^{\dagger}\,\sigma_{\nu}\,S^{-1}.~ \] 证明

　　 上述带指标的记号形式确实是正确的，这一点并非立即显而易见。部分原因是，在使用指标记号时，很容易将一个洛伦兹变换与它的逆，或其转置相混淆。这种混淆源于以下恒等式在指标形式下难以识别：$\eta \Lambda^{\textsf{T}} \eta = \Lambda^{-1}$.

　　 需要强调的是，洛伦兹变换本身并不是在洛伦兹变换下的张量！因此，对这一恒等式给出一个直接证明是有用的，以确立其正确性。

　　 证明可以从如下恒等式出发： \[ \omega \sigma^{k} \omega^{-1} = -(\sigma^{k})^{\textsf{T}} = -(\sigma^{k})^{*}, \qquad k = 1,2,3,~ \] 其中 $\sigma^{k}$ 是通常的泡利矩阵，$(\cdot)^{\textsf{T}}$ 表示矩阵转置，$(\cdot)^{*}$ 表示复共轭。矩阵 $\omega$ 定义为 \[ \omega = i\sigma_{2} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}.~ \] 写成四矢量形式，上述关系为 \[ \sigma_{\mu}^{\textsf{T}} = \sigma_{\mu}^{*} = \omega \,\overline{\sigma}_{\mu}\, \omega^{-1}.~ \] 其变换规律为 \[ \begin{aligned} \sigma_{\mu}^{\textsf{T}} {\Lambda^{\mu}}_{\nu} &= \omega \,\overline{\sigma}_{\mu}\, \omega^{-1} {\Lambda^{\mu}}_{\nu} \\ &= \omega S \,\overline{\sigma}_{\nu}\, S^{\dagger} \omega^{-1} \\ &= \bigl(\omega S \omega^{-1}\bigr)\, \bigl(\omega \overline{\sigma}_{\nu} \omega^{-1}\bigr)\, \bigl(\omega S^{\dagger} \omega^{-1}\bigr) \\ &= \bigl(S^{-1}\bigr)^{\textsf{T}} \,\sigma_{\nu}^{\textsf{T}}\, \bigl(S^{-1}\bigr)^{*}. \end{aligned}~ \] 再取一次转置，得到 \[ \sigma_{\mu}\,{\Lambda^{\mu}}_{\nu} = \bigl(S^{-1}\bigr)^{\dagger}\,\sigma_{\nu}\,S^{-1}.~ \]

辛群

　　 辛群 $Sp(2,\mathbf{C})$ 与 $SL(2,\mathbf{C})$ 同构。该同构的构造方式是保持 $\mathbf{C}^{2}$ 上的一个辛双线性型不变，即要求该形式在洛伦兹变换下保持不变。其表述如下： \[ \operatorname{Sp}(2,\mathbf{C}) = \{\, S \in \operatorname{GL}(2,\mathbf{C}) : S^{\textsf{T}} \,\omega\, S = \omega \,\},~ \] 其中 \[ \omega = i\sigma_{2} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}.~ \] 对该矩阵的其他常见记号是 $\omega = \epsilon$；有时也写作 $J$，但这容易引起混淆，因为 “几乎复结构” 与之并不相同，它们的变换方式也不同。

　　 辛群 $Sp(2,\mathbb{C})$ 与 $SL(2,\mathbb{C})$ 同构。该同构的构造方式是保持 $\mathbb{C}^{2}$ 上的一个辛双线性型不变，即要求该形式在洛伦兹变换下保持不变。其表述如下： \[ \operatorname{Sp}(2,\mathbf{C}) = \{\, S \in \operatorname{GL}(2,\mathbb{C}) : S^{\textsf{T}} \,\omega\, S = \omega \,\},~ \] 其中 \[ \omega = i\sigma_{2} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}.~ \] 对该矩阵的其他常见记号是 $\omega = \epsilon$；有时也写作 $J$，但这容易引起混淆，因为 “几乎复结构” 与之并不相同，它们的变换方式也不同。

　　 给定一对外尔旋量（即二维旋量） \[ u = \begin{bmatrix} u_{1} \\ u_{2} \end{bmatrix}, \quad v = \begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix},~ \] 其不变双线性型通常写作 \[ \langle u, v \rangle = -\langle v, u \rangle = u_{1}v_{2} - u_{2}v_{1} = u^{\textsf{T}} \omega v.~ \] 这一形式在洛伦兹群作用下保持不变，即对于任意 $S \in SL(2,\mathbb{C})$，有 \[ \langle Su, Sv \rangle = \langle u, v \rangle.~ \] 该形式定义了一种旋量的 “标量积”，并且常用于在拉格朗日量中定义洛伦兹不变的质量项。它具有若干对物理学非常重要的性质，其中之一是 \[ \omega^{2} = -1, \qquad \omega^{-1} = \omega^{\textsf{T}} = \omega^{\dagger} = -\omega.~ \] 其定义关系可写作 \[ \omega S^{\textsf{T}} \omega^{-1} = S^{-1},~ \] 这与洛伦兹群的定义关系十分相似： \[ \eta \Lambda^{\textsf{T}} \eta^{-1} = \Lambda^{-1},~ \] 其中 $\eta = \operatorname{diag}(+1, -1, -1, -1)$ 是闵可夫斯基空间的度规张量，且 $\Lambda \in SO(1,3)$。

4. 覆盖群

　　 由于 $SL(2,\mathbb{C})$ 是单连通的，它是受限洛伦兹群 $SO^{+}(1,3)$ 的普适覆盖群。通过限制，可以得到一个同态 $SU(2) \to SO(3)$。这里，特殊酉群 $SU(2)$ 与单位范数四元数群同构，并且也是单连通的，因此它是旋转群 $SO(3)$ 的覆盖群。

　　 这些覆盖映射都是二重覆盖，其意义是覆盖群中的恰好两个元素映射到商群的同一个元素。通常会说，受限洛伦兹群和旋转群都是 “双重连通的”。这意味着每个群的基本群都同构于二元循环群 $\mathbb{Z}_{2}$。

　　 二重覆盖是自旋群的特征。实际上，除了以下二重覆盖 \[ \operatorname{Spin}^{+}(1,3) = SL(2,\mathbf{C}) \;\longrightarrow\; SO^{+}(1,3),~ \] \[ \operatorname{Spin}(3) = SU(2) \;\longrightarrow\; SO(3),~ \] 之外，还有 \[ \operatorname{Pin}(1,3) \;\longrightarrow\; O(1,3),~ \] \[ \operatorname{Spin}(1,3) \;\longrightarrow\; SO(1,3),~ \] \[ \operatorname{Spin}^{+}(1,2) = SU(1,1) \;\longrightarrow\; SO(1,2).~ \] 这些自旋的二重覆盖是通过克利福德代数构造出来的。

5. 拓扑

　　 在二重覆盖 \[ SU(2) \;\longrightarrow\; SO(3)~ \] 中，左群与右群分别是二重覆盖 \[ SL(2,\mathbf{C}) \;\longrightarrow\; SO^{+}(1,3)~ \] 中左群与右群的变形收缩。

　　 然而，齐性空间 $SO^{+}(1,3) / SO(3)$ 同胚于三维双曲空间 $H^{3}$。因此，可以将受限洛伦兹群描述为一个以 $SO(3)$ 为纤维、以 $H^{3}$ 为底空间的主纤维丛。由于后者同胚于 $\mathbf{R}^{3}$，而 $SO(3)$ 同胚于三维实射影空间 $\mathbf{RP}^{3}$，我们看到受限洛伦兹群在局部上同胚于 $\mathbf{RP}^{3}$ 与 $\mathbf{R}^{3}$ 的直积。

　　 由于底空间是可缩的，这一局部同胚可以扩展为一个整体同胚。

6. 共轭类

　　 由于受限洛伦兹群 $SO^{+}(1,3)$ 与莫比乌斯群 $PSL(2,\mathbb{C})$ 同构，它的共轭类也分为五类：

　　 在关于莫比乌斯变换的文章中，解释了这种分类是如何通过考虑莫比乌斯变换在黎曼球面上的不动点而产生的；在这里，这对应于受限洛伦兹变换在闵可夫斯基时空中的零特征子空间。

　　 下面的小节中将给出每一类的示例，以及其生成的一参数子群的作用效果（例如，对夜空外观的影响）。

　　 莫比乌斯变换是黎曼球面（或天球）的共形变换。然后，通过与 $SL(2,\mathbb{C})$ 中任意元素的共轭，可以分别得到任意椭圆型、双曲型、螺旋型和抛物型的（受限）洛伦兹变换示例。相应一参数子群的流线效果是：将示例中看到的模式通过某种共形变换映射过去。例如，一个椭圆型洛伦兹变换可以在天球上具有任意两个不同的不动点，但点仍沿着圆弧从一个不动点流向另一个不动点。其他几种情况与此类似。

椭圆变换

　　 $SL(2,\mathbf{C})$ 的一个椭圆元素为 \[ P_{1} = \begin{bmatrix} \exp\!\left(\tfrac{i}{2}\theta\right) & 0 \\ 0 & \exp\!\left(-\tfrac{i}{2}\theta\right) \end{bmatrix},~ \] 它具有不动点 $\xi = 0, \infty$。将作用写作 $X \;\mapsto\; P_{1} X P_{1}^{\dagger}$,并整理各项后，旋量映射将其转化为如下（受限）洛伦兹变换： \[ Q_{1} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\left(\theta\right) & \sin\left(\theta\right) & 0 \\ 0 & - \sin\left(\theta\right) & \cos\left(\theta\right) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \exp\!\left( \theta \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \right).~ \]

　　 该变换表示绕 $z$ 轴的旋转，即 $ \exp\left(i\theta J_{z}\right) $。它生成的一参数子群是通过将 $\theta$ 视为一个实变量（旋转角度），而非常数得到的。

　　 在天球上的相应连续变换（除了恒等变换以外）都具有相同的两个不动点：北极与南极。该变换将其他点沿纬线圈移动，因此该群在 $\theta$ 增大时产生绕 $z$ 轴的连续逆时针旋转。旋量映射中显现的角度加倍现象是自旋二重覆盖的一个典型特征。

双曲变换

　　 $SL(2,\mathbf{C})$ 的一个双曲元素为 \[ P_{2} = \begin{bmatrix} \exp\!\left(\tfrac{\eta}{2}\right) & 0 \\ 0 & \exp\!\left(-\tfrac{\eta}{2}\right) \end{bmatrix},~ \] 它具有不动点 $\xi = 0, \infty$。在从黎曼球面到欧几里得平面的立体投影下，该莫比乌斯变换的效果是一个从原点出发的伸缩变换。

　　 旋量映射将其转化为如下洛伦兹变换： \[ Q_{2} = \begin{bmatrix} \cosh\left(\eta\right) & 0 & 0 & \sinh\left(\eta\right) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \sinh\left(\eta\right) & 0 & 0 & \cosh\left(\eta\right) \end{bmatrix} = \exp\!\left( \eta \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \right).~ \] 该变换表示沿 $z$ 轴、快度为 $\eta$ 的推动。它生成的一参数子群是通过将 $\eta$ 视为一个实变量（快度），而非常数得到的。在天球上的相应连续变换（除恒等变换外）都具有相同的不动点（北极与南极），并将其他点沿经线移动，从南极远离并趋向北极。

螺旋变换

　　 $SL(2,\mathbf{C})$ 的一个螺旋元素为 \[ P_{3} = P_{2}P_{1} = P_{1}P_{2} = \begin{bmatrix} \exp\!\left(\tfrac{1}{2}(\eta + i\theta)\right) & 0 \\ 0 & \exp\!\left(-\tfrac{1}{2}(\eta + i\theta)\right) \end{bmatrix},~ \] 它具有不动点 $\xi = 0, \infty$。旋量映射将其转化为洛伦兹变换 \[ Q_{3} = Q_{2}Q_{1} = Q_{1}Q_{2} = \begin{bmatrix} \cosh\left(\eta\right) & 0 & 0 & \sinh\left(\eta\right) \\ 0 & \cos\left(\theta\right) & \sin\left(\theta\right) & 0 \\ 0 & - \sin\left(\theta\right) & \cos\left(\theta\right) & 0 \\ \sinh\left(\eta\right) & 0 & 0 & \cosh\left(\eta\right) \end{bmatrix} = \exp\!\begin{bmatrix} 0 & 0 & 0 & \eta \\ 0 & 0 & \theta & 0 \\ 0 & -\theta & 0 & 0 \\ \eta & 0 & 0 & 0 \end{bmatrix}.~ \] 它生成的一参数子群是通过将 $\eta + i\theta$ 替换为该复常数的任意实数倍得到的。（如果 $\eta$ 和 $\theta$ 独立变化，则得到一个二维阿贝尔子群，它由绕 $z$ 轴的旋转与沿 $z$ 轴的推动同时组成；相比之下，这里讨论的一维子群由该二维子群中的那些元素构成，其推动的快度与旋转的角度具有固定比值。）

　　 在天球上的相应连续变换（除恒等变换外）都具有相同的两个不动点（北极与南极）。这些变换将其他点沿着一族称为螺旋线的曲线，从南极远离并趋向北极（或反之）。每条螺旋线都会在每个极点无限次地盘旋。

抛物变换

　　 $SL(2,\mathbf{C})$ 的一个抛物元素为 \[ P_{4} = \begin{bmatrix} 1 & \alpha \\ 0 & 1 \end{bmatrix},~ \] 它在黎曼球面上的唯一不动点为 $\xi = \infty$。在立体投影下，它表现为沿实轴的平移。

　　 旋量映射将其转化为矩阵（代表一个洛伦兹变换）： \[ Q_{4} = \begin{bmatrix} 1 + \tfrac{1}{2}|\alpha|^{2} & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & -\tfrac{1}{2}|\alpha|^{2} \\ \operatorname{Re}(\alpha) & 1 & 0 & -\operatorname{Re}(\alpha) \\ -\operatorname{Im}(\alpha) & 0 & 1 & \operatorname{Im}(\alpha) \\ \tfrac{1}{2}|\alpha|^{2} & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & 1 - \tfrac{1}{2}|\alpha|^{2} \end{bmatrix} = \exp \begin{bmatrix} 0 & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & 0 \\ \operatorname{Re}(\alpha) & 0 & 0 & -\operatorname{Re}(\alpha) \\ -\operatorname{Im}(\alpha) & 0 & 0 & \operatorname{Im}(\alpha) \\ 0 & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & 0 \end{bmatrix}.~ \] 它生成了一个二维阿贝尔子群，这是通过将 $\alpha$ 视为复变量而非常数得到的。在天球上的相应连续变换（除了恒等变换外），将各点沿着一族圆移动，这些圆在北极都与某一条大圆相切。除北极本身外的所有点都沿着这些圆运动。

　　 抛物型洛伦兹变换常被称为零旋转。由于在四类非恒等洛伦兹变换（椭圆、双曲、螺旋、抛物）中，这类变换可能是最不熟悉的，因此这里给出一个示例，说明如何确定抛物型洛伦兹变换在闵可夫斯基时空上的作用。

　　 上文所给的矩阵导致如下变换： \[ \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} \;\longrightarrow\; \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} + \operatorname{Re}(\alpha) \begin{bmatrix} x \\ t-z \\ 0 \\ x \end{bmatrix} - \operatorname{Im}(\alpha) \begin{bmatrix} y \\ 0 \\ z-t \\ y \end{bmatrix} + \tfrac{|\alpha|^{2}}{2} \begin{bmatrix} t-z \\ 0 \\ 0 \\ t-z \end{bmatrix}.~ \] 现在，不失一般性，取 $\operatorname{Im}(\alpha) = 0$。对该变换关于实参数 $\alpha$ 求导，并在 $\alpha=0$ 处取值，得到相应的向量场（即一阶线性偏微分算子）： \[ x\left(\partial_{t} + \partial_{z}\right) + (t-z)\,\partial_{x}.~ \] 将其作用于函数 $f(t,x,y,z)$，并要求其保持不变；也就是说，该算子湮灭此函数。由此得到的一阶线性偏微分方程的解可表示为 \[ f(t,x,y,z) = F\bigl(y,\, t-z,\, t^{2}-x^{2}-z^{2}\bigr),~ \] 其中 $F$ 是任意光滑函数。$F$ 的自变量给出了三个不变量，它们描述了点（事件）在此抛物变换下的运动方式，而它们自身并不发生改变： \[ y = c_{1}, \quad t-z = c_{2}, \quad t^{2} - x^{2} - z^{2} = c_{3}.~ \] 对右边常数取实数值即可得到三个条件，从而在闵可夫斯基时空中刻画出一条曲线。该曲线即为此变换的一个轨道。

　　 这些有理不变量的形式表明，这些流线（轨道）有一个简单的描述：忽略无关的坐标 $y$，每条轨道都是一个零平面 $t = z + c_{2}$, 与一个双曲面 $t^{2} - x^{2} - z^{2} = c_{3}$ 的交集。当 $c_{3} = 0$ 时，双曲面退化为光锥，此时轨道变为位于相应零平面中的抛物线。

　　 光锥上的一条特殊零直线保持不变；这对应于上文所述黎曼球面上的唯一（重）不动点。通过原点的其他零直线则被该变换 “绕着光锥摆动”。当参数 $\alpha$ 增大时，沿着这样一条零直线的运动对应于天球上某个点沿圆形流线的运动，如前所述。

　　 若选择 $\operatorname{Re}(\alpha) = 0$，则产生类似的轨道，只是此时 $x$ 与 $y$ 的角色对换。

　　 抛物型变换导致无质量粒子（如光子）的规范对称性，其螺旋度满足 $|h|\geq 1$。在上述显式示例中，一个沿 $z$ 方向运动的无质量粒子，其四动量为 $P = (p, 0, 0, p)$,完全不受由 $x$ 推动与 $y$ 旋转组合 $K_{x} - J_{y}$ 所定义的变换影响，该组合属于其运动的 “小群”。从上文的显式变换律可以清楚地看出：像任意类光向量一样，$P$ 本身是不变的；换言之，$\alpha$ 的所有痕迹或效应都消失了。在此特殊情形下，$c_{1} = c_{2} = c_{3} = 0$。（另一个类似的生成元 $K_{y} + J_{x}$，以及它和 $J_{z}$ 一起，共同构成了该类光向量的小群，其同构于欧几里得群 $E(2)$。）

夜空的外观

　　 这一同构的结果是：黎曼球面的莫比乌斯变换可以表示洛伦兹变换如何改变夜空的外观，即由相对于 “固定恒星” 以相对论速度运动的观察者所看到的图像。

　　 假设 “固定恒星” 存在于闵可夫斯基时空中，并由天球上的点来建模。则天球上的一个给定点可以与复数 $\xi = u + iv$ 关联，该复数对应于黎曼球面上的一点，并且可以与闵可夫斯基空间中的一个零向量（类光向量）相对应： \[ \begin{bmatrix} u^{2} + v^{2} + 1 \\ 2u \\ -2v \\ u^{2} + v^{2} - 1 \end{bmatrix},~ \] 或者，在 Weyl 表示（旋量映射）下，对应的厄米矩阵为 \[ N = 2 \begin{bmatrix} u^{2} + v^{2} & u + iv \\ u - iv & 1 \end{bmatrix}.~ \] 该零向量的实数倍集合称为通过原点的零直线，它表示一条从某一时空位置的观察者（我们可以将其识别为闵可夫斯基时空的原点）指向各种遥远天体（例如恒星）的视线。于是，天球上的点（等价于视线）可以与某些厄米矩阵相对应。

　　 射影几何与二维球面的不同视角

　　 在射影几何的语言中，这一图像得到了清晰的呈现。（受限）洛伦兹群作用在射影天球上。射影天球是非零零向量的空间，其中 $t > 0$，并在射影空间的商关系下定义： \[ (t,x,y,z) \sim (t',x',y',z') \quad\Longleftrightarrow\quad (t',x',y',z') = (\lambda t,\, \lambda x,\, \lambda y,\, \lambda z), \quad \lambda > 0.~ \] 这被称为天球，因为这样可以在施加洛伦兹变换后，将时间坐标 $t$ 重标度为 $1$，从而保证空间部分位于单位球面上。

　　 从莫比乌斯变换的角度，$SL(2,\mathbb{C})$ 作用于复射影空间 $\mathbb{CP}^{1}$，而 $\mathbb{CP}^{1}$ 可证明与二维球面微分同胚——这通常称为黎曼球面。射影空间的商结构会诱导出群 $SL(2,\mathbb{C})$ 上的相应商结构。

　　 最后，可以通过使用复射影向量构造零向量，将这两者联系起来。若 $\xi$ 是 $\mathbb{CP}^{1}$ 的一个射影向量，它可以与其厄米共轭张量化，得到一个 $2 \times 2$ 的厄米矩阵。正如本文其他部分所述，该矩阵空间可以视为 4-向量。而由黎曼球面上每个射影向量转化为矩阵所形成的矩阵空间，被称为Bloch 球。

7. 李代数

　　 与任何李群一样，研究洛伦兹群的许多方面的一个有用方法是通过它的李代数。由于洛伦兹群 $SO(1,3)$ 是一个矩阵李群，它对应的李代数 $\mathfrak{so}(1,3)$ 是一个矩阵李代数，可以表示为 \(^\text{[5]}\)： \[ \mathfrak{so}(1,3) = \{\, 4\times 4 \ \mathbf{R}\text{-值矩阵 } X \;\mid\; e^{tX} \in SO(1,3) \ \text{对所有 } t \,\}.~ \] 若 $\eta$ 是对角矩阵 $\operatorname{diag}(1,-1,-1,-1)$，则李代数 $\mathfrak{o}(1,3)$ 由满足条件 \[ \eta X \eta = -X^{\textsf{T}}~ \] 的 $4 \times 4$ 矩阵 $X$ 组成 \(^\text{[6]}\)。

　　 具体而言，$\mathfrak{so}(1,3)$ 由如下形式的 $4\times 4$ 矩阵构成： \[ \begin{pmatrix} 0 & a & b & c \\ a & 0 & d & e \\ b & -d & 0 & f \\ c & -e & -f & 0 \end{pmatrix},~ \] 其中 $a,b,c,d,e,f$ 为任意实数。该李代数是六维的。当 $a=b=c=0$ 时得到的子代数同构于 $\mathfrak{so}(3)$。

　　 完整的洛伦兹群 $O(1,3)$、正规洛伦兹群 $SO(1,3)$ 以及正规正时间洛伦兹群 $SO^{+}(1,3)$（与恒等元连通的分支）都具有相同的李代数，通常记作 $\mathfrak{so}(1,3)$。

　　 由于洛伦兹群的恒等分支同构于 $SL(2,\mathbf{C})$ 的有限商（参见上文关于洛伦兹群与莫比乌斯群的联系部分），因此洛伦兹群的李代数同构于李代数 $\mathfrak{sl}(2,\mathbf{C})$。作为一个复李代数，$\mathfrak{sl}(2,\mathbf{C})$ 是三维的；但当视为实李代数时，它是六维的。

洛伦兹代数的对易关系

　　 标准基矩阵可以标记为 $M^{\mu \nu}$，其中 $\mu,\nu \in \{0,1,2,3\}$。这些基矩阵的构造方式是：依次只令 $a,b,\cdots,f$ 中的一个为 $1$，其余为 $0$。其分量可写为 \[ {(M^{\mu \nu})^{\rho}}_{\sigma} \;=\; \eta^{\nu \sigma} {\delta^{\rho}}_{\mu} - \eta^{\mu \sigma} {\delta^{\rho}}_{\nu}.~ \] 它们的对易关系为 \[ [M^{\mu \nu}, M^{\rho \sigma}] = M^{\mu \sigma}\,\eta^{\nu \rho} - M^{\nu \sigma}\,\eta^{\mu \rho} + M^{\nu \rho}\,\eta^{\mu \sigma} - M^{\mu \rho}\,\eta^{\nu \sigma}.~ \] 在使用上可能存在不同的约定。在物理学中，通常在基元中附加一个因子 $i$，从而在对易关系中也会出现因子 $i$。

　　 其中，$M^{0i}$ 生成推动，而 $M^{ij}$ 生成旋转。

　　 洛伦兹代数的结构常数可以直接从对易关系中读出。任何满足这些关系的

推动与旋转的生成元

　　 洛伦兹群可以看作 $\mathbf{R}^{4}$ 的微分同胚群的一个子群，因此它的李代数可以与 $\mathbf{R}^{4}$ 上的向量场对应。特别地，在一个空间上生成等距变换的向量称为Killing 向量，它为计算李代数提供了一种方便的替代方法（相对于左不变向量场）。我们可以写出一组六个生成元：

　　 这里引入因子 $i$ 是为了确保旋转的生成元是厄米的。

　　 回顾一下如何由一个向量场（写作一阶线性偏微分算子）得到一参数群是有帮助的。例如， \[ \mathcal{L} = -y\partial_{x} + x\partial_{y}.~ \] 对应的初值问题（设 $r = (x,y)$ 是标量 $\lambda$ 的函数，并解 $\partial_{\lambda} r = \mathcal{L}r$ 配合某些初始条件）为 \[ \frac{\partial x}{\partial \lambda} = -y, \quad \frac{\partial y}{\partial \lambda} = x, \quad x(0) = x_{0}, \quad y(0) = y_{0}.~ \] 其解为 \[ x(\lambda) = x_{0} \cos\left(\lambda\right) - y_{0} \sin\left(\lambda\right) , \quad y(\lambda) = x_{0} \sin\left(\lambda\right) + y_{0} \cos\left(\lambda\right) ,~ \] 或者写作矩阵形式： \[ \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\left(\lambda\right) & - \sin\left(\lambda\right) & 0 \\ 0 & \sin\left(\lambda\right) & \cos\left(\lambda\right) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} t_{0} \\ x_{0} \\ y_{0} \\ z_{0} \end{bmatrix}.~ \] 我们很容易识别出这是绕 $z$ 轴的旋转一参数矩阵群 $ \exp\left(i\lambda J_{z}\right) $。

　　 对群参数 $\lambda$ 求导，并在 $\lambda = 0$ 处取值，我们得到标准矩阵： \[ iJ_{z} = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix},~ \] 它正对应于我们一开始所使用的向量场。这说明了如何在李代数元素的矩阵表示与向量场表示之间切换。指数映射在此扮演了特殊的角色，这不仅适用于洛伦兹群，而且适用于一般的李群。

　　 反过来，按照上一节的程序，我们看到与六个生成元对应的莫比乌斯变换，分别来自于将三个 Pauli 矩阵乘以 $\eta/2$（对应三个推动）或 $i\theta/2$（对应三个旋转）后再取指数： \[ \sigma_{1} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \quad \sigma_{2} = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}, \quad \sigma_{3} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}.~ \]

莫比乌斯群的生成元

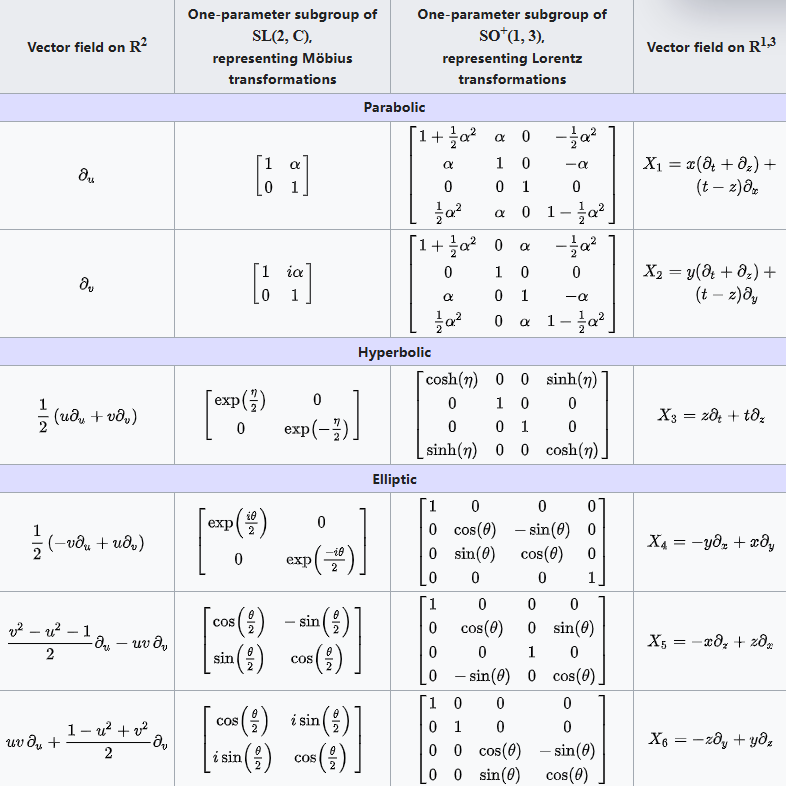
　　 另一组生成元来自于与莫比乌斯群的同构。下表列出了六个生成元，其中：

　　 需要注意的是，这些生成元由以下部分构成：

图
图 4

　　 示例：绕 $y$ 轴的旋转

　　 从 \[ \sigma_{2} = \begin{bmatrix} 0 & i \\ - i & 0 \end{bmatrix}~ \] 开始。

　　 取指数： \[ \exp\!\left(\tfrac{i\theta}{2}\sigma_{2}\right) = \begin{bmatrix} \cos\!\left(\tfrac{\theta}{2}\right) & -\sin\!\left(\tfrac{\theta}{2}\right) \\ \sin\!\left(\tfrac{\theta}{2}\right) & \cos\!\left(\tfrac{\theta}{2}\right) \end{bmatrix}.~ \] 该 $SL(2,\mathbf{C})$ 元素表示一参数（椭圆型）莫比乌斯变换子群： \[ \xi \;\mapsto\; \xi' = \frac{\cos\!\left(\tfrac{\theta}{2}\right)\,\xi - \sin\!\left(\tfrac{\theta}{2}\right)} {\sin\!\left(\tfrac{\theta}{2}\right)\,\xi + \cos\!\left(\tfrac{\theta}{2}\right)}.~ \] 接下来， \[ \left.\frac{d\xi'}{d\theta}\right|_{\theta = 0} = -\frac{1+\xi^{2}}{2}.~ \] 对应的 $C$ 上的向量场（可看作 $S^{2}$ 在立体投影下的像）为 \[ -\frac{1+\xi^{2}}{2}\,\partial_{\xi}.~ \] 若写作 $\xi = u + iv$，则该向量场在 $\mathbb{R}^{2}$ 上为 \[ -\frac{1+u^{2}-v^{2}}{2}\,\partial_{u} - uv\,\partial_{v}.~ \] 回到我们的 $SL(2,\mathbf{C})$ 元素，写出其作用 $X \;\mapsto\; PXP^{\dagger}$,并整理各项，可以发现其在旋量映射下的像为 $SO^{+}(1,3)$ 中的元素： \[ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\left(\theta\right) & 0 & \sin\left(\theta\right) \\ 0 & 0 & 1 & 0 \\ 0 & - \sin\left(\theta\right) & 0 & \cos\left(\theta\right) \end{bmatrix}.~ \] 对 $\theta$ 在 $\theta=0$ 处求导，得到在 $\mathbf{R}^{1,3}$ 上对应的向量场： \[ z\partial_{x} - x\partial_{z}.~ \] 这显然是绕 $y$ 轴逆时针旋转的生成元。

8. 洛伦兹群的子群

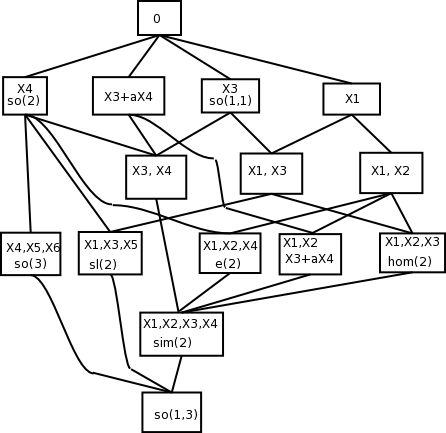
　　 洛伦兹群李代数的子代数可以按共轭分类枚举出来，从而受限洛伦兹群的闭子群也可以按共轭分类列出。（详见下文引用的 Hall 著作。）这些子代数可以方便地用上表所给的生成元 $X_{n}$ 来表示。

　　 一维子代数显然对应于洛伦兹群元素的四类共轭类：

　　 （严格来说，最后一种情况对应无穷多个类，因为不同的 $a$ 给出不同的类。） 二维子代数如下：

　　 三维子代数按照 Bianchi 分类方案：

　　 Bianchi 类型指的是意大利数学家 Luigi Bianchi 对三维李代数的分类。

图
图 5：李代数 $\mathfrak{so}(1,3)$ 的子代数格（模共轭）

　　 与任意连通李群一样，受限洛伦兹群的闭子群的陪集空间（即齐性空间）具有重要的数学意义。以下是几个简要描述：

9. 推广到更高维度

　　 洛伦兹群的概念可以自然推广到任意维的时空。数学上，$(n+1)$ 维闵可夫斯基空间的洛伦兹群是不定正交群 $O(n,1)$，它由保持如下二次型的线性变换组成： $$ (x_{1},x_{2},\ldots ,x_{n},x_{n+1}) ;\mapsto; x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}-x_{n+1}^{2}.~ $$ 群(O(1,n))保持的二次型为： $$ (x_{1},x_{2},\ldots ,x_{n},x_{n+1}) ;\mapsto; x_{1}^{2}-x_{2}^{2}-\cdots -x_{n+1}^{2}.~ $$ $O(1,n)$ 与 $O(n,1)$ 互为同构，这两种表示在理论物理界都被广泛使用：前者更常见于与引力相关的文献，而后者更常见于粒子物理学文献。

　　 一个常见的记号是将配备这种二次型的向量空间 $\mathbf{R}^{n+1}$ 记为 $\mathbf{R}^{1,n}$。

　　 四维情况（即 $(n=3)$）下洛伦兹群的许多性质可以直接推广到任意 $n$。例如，洛伦兹群 $O(n,1)$ 有四个连通分支，并且它通过共形变换作用于 $(n-1)$ 维的天球，即 $(n+1)$ 维闵可夫斯基空间中的 $(n-1)$ 维球面。其单位元连通分支 $SO^{+}(n,1)$ 是一个以 $SO(n)$ 为纤维、底空间为双曲 $n$ 空间 $H^{n}$ 的丛。

　　 低维情况 $n=1,2$ 常常作为物理情形 $n=3$ 的 “玩具模型”。而高维洛伦兹群则在一些物理理论（如弦论）中出现，这些理论假设存在隐藏维度。

　　 此外，洛伦兹群 $O(n,1)$ 也是 $n$ 维 de Sitter 空间 $dS_{n}$ 的等距群，其中 $dS_{n}$ 可以表示为齐性空间 $$ dS_{n} ;\cong; O(n,1)/O(n-1,1).~ $$ 特别地，$O(4,1)$ 是四维 de Sitter 宇宙 $dS_{4}$ 的等距群，这是一个宇宙学模型。

10. 另见

11. 注释

　　
a,一些作者在提及 (SO^{+}(1,3)) 时，使用 (SO(1,3)) 甚至 (O(1,3)) 来表示。
b,具体推导可参见 *Weyl 方程* 一文。

12. 参考文献

  1. Weinberg, 2002
  2. Varićak, V. 1910. Theory of Relativity and Lobachevskian Geometry, Phys Z 1910, §3 “Lorentz–Einstein transformation as translation”. 英译见 Wikipedia.
  3. Gelfand, Minlos & Shapiro, 1963
  4. Wigner, 1939
  5. Hall, 2015, 定义 3.18
  6. Hall, 2015, 命题 3.25

13. 阅读书目

                     

© 保留一切权利