零点能量（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 零点能（ZPE）是量子力学系统可能具有的最低能量。与经典力学不同，量子系统即使在最低能量状态下也会不断波动，这可以通过海森堡不确定性原理来描述[1]。因此，即使在绝对零度下，原子和分子也会保持某些振动运动。除了原子和分子外，真空的空旷空间也具有这些性质。根据量子场论，宇宙可以被看作不仅是孤立的粒子，而是连续波动的场：物质场，其量子是费米子（即轻子和夸克），以及力场，其量子是玻色子（例如光子和胶子）。所有这些场都有零点能[2]。这些波动的零点场导致了一种在物理学中重新引入以太的现象[1][3]，因为某些系统可以探测到这种能量的存在[需要引用]。然而，如果这个以太要保持洛伦兹不变性，以保证与爱因斯坦的相对论没有矛盾，那么它就不能被视为一种物理介质[1]。

　　 零点能的概念对宇宙学也非常重要，然而，物理学目前缺乏一个完整的理论模型来理解宇宙学中的零点能；特别是理论上与观测到的宇宙真空能量之间的差异，成为了一个重大争议问题[4]。然而，根据爱因斯坦的广义相对论，任何这种能量都会引起引力，而来自宇宙膨胀、暗能量和 Casimir 效应的实验证据表明，任何这种能量都极其微弱。一个试图解决这一问题的提案是认为费米子场具有负的零点能，而玻色子场具有正的零点能，因此这些能量会以某种方式相互抵消[5][6]。如果超对称是自然界的精确对称性，这个想法是成立的；然而，欧洲核子研究中心的大型强子对撞机至今未找到支持这一理论的证据。此外，已知如果超对称是有效的，它最多也只是一个破缺的对称性，仅在极高的能量下才成立，目前没有人能够展示一个低能宇宙中发生零点能抵消的理论[6]。这一差异被称为宇宙学常数问题，是物理学中最大的未解之谜之一。许多物理学家认为，“真空是理解自然的关键”[7]。

1. 词源和术语

　　 零点能（ZPE）一词是从德语 “Nullpunktsenergie” 翻译过来的。[8] 有时，它与零点辐射和基态能量互换使用。零点场（ZPF）一词可以用来指代特定的真空场，例如量子电动力学（QED）真空，它专门处理量子电动力学（如光子、电子和真空之间的电磁相互作用），或者量子色动力学（QCD）真空，它涉及量子色动力学（如夸克、胶子和真空之间的色荷相互作用）。真空可以被视为不是空的空间，而是所有零点场的组合。在量子场论中，这种场的组合被称为真空态，与之相关的零点能量被称为真空能量，平均能量值称为真空期望值（VEV），也称为其凝聚态。

2. 概述

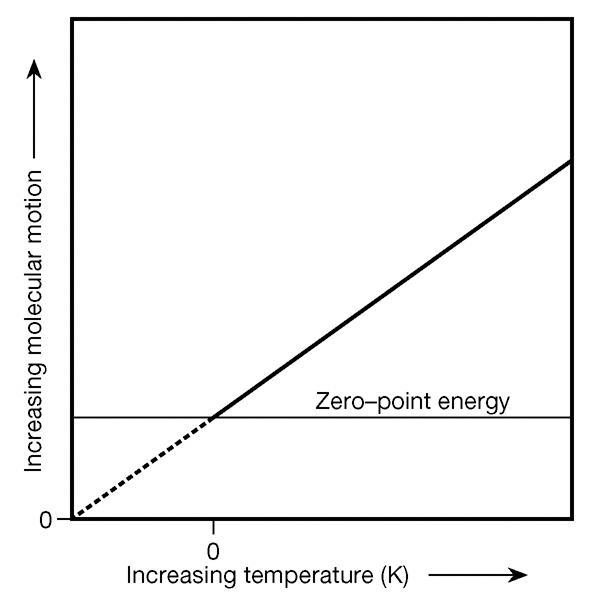
　　 在经典力学中，所有粒子都可以被认为具有某种能量，这种能量由它们的势能和动能组成。例如，温度来自于由动能引起的随机粒子运动的强度（称为布朗运动）。当温度降低到绝对零度时，可以认为所有运动都停止，粒子完全静止。然而，实际上，即使在最低的温度下，粒子仍然保持动能。与这种零点能量对应的随机运动永远不会消失；它是量子力学不确定性原理的结果。

　　 不确定性原理表明，任何物体无法同时拥有精确的位置和速度值。量子力学物体的总能量（包括势能和动能）由其哈密顿量描述，哈密顿量也描述了该系统作为一个简谐振子或波函数，在不同的能量状态之间波动（参见波粒二象性）。所有量子力学系统即使在其基态下也会经历波动，这是它们波动性本质的结果。不确定性原理要求每个量子力学系统必须具有大于经典势阱最小值的波动零点能量。这导致即使在绝对零度下也会有运动。例如，液氦在大气压力下无论温度如何都不会冻结，这正是由于其零点能量。

　　 根据阿尔伯特·爱因斯坦的质量与能量等价关系 \( E = mc^2 \)，任何包含能量的空间点都可以被看作具有质量，从而产生粒子。现代物理学已经发展出了量子场论（QFT），用以理解物质与力之间的基本相互作用；它将空间中的每个点视为一个量子简谐振子。根据量子场论，宇宙由物质场组成，物质场的量子是费米子（如轻子和夸克），以及力场，力场的量子是玻色子（如光子和胶子）。所有这些场都具有零点能量。最近的实验支持这样一个观点：粒子本身可以看作是基础量子真空的激发态，物质的所有属性只是由零点场相互作用引起的真空波动。

　　 ‘空’空间可以具有内在能量，并且没有‘真正的真空’这一概念，这一观点似乎是反直觉的。通常认为，整个宇宙完全浸泡在零点辐射中，因此它只能在计算中增加一个常数值。因此，物理测量将仅揭示该值的偏差。[10] 对于许多实际计算，零点能量通常被在数学模型中以强制性的方式忽略，作为一个没有物理效应的项。然而，这种处理方式会引发问题，因为在爱因斯坦的广义相对论中，空间的绝对能量值不是一个任意常数，而是产生了宇宙学常数。几十年来，大多数物理学家认为，存在某种尚未发现的基本原理，能够消除无限的零点能量并使其完全消失。如果真空没有内在的、绝对的能量值，它就不会发生引力效应。人们曾认为，随着宇宙从大爆炸的余波中膨胀，任何单位的空旷空间中所包含的能量将减少，因为总能量扩展以填满宇宙的体积；宇宙中的星系和所有物质应该开始减速。然而，1998 年通过发现宇宙的膨胀并没有减缓，而是加速了，这一可能性被排除。这意味着空空间确实具有某种内在的能量。暗能量的发现最好通过零点能量来解释，尽管目前仍然是一个谜，为什么其值与通过理论得到的巨大值相比如此之小——这就是宇宙学常数问题。[5]

　　 许多归因于零点能量的物理效应已经通过实验验证，如自发辐射、卡西米尔力、兰姆位移、电子的磁矩和德尔布吕克散射。[11][12] 这些效应通常被称为‘辐射修正’。[13] 在更复杂的非线性理论中（例如量子色动力学，QCD），零点能量可以引发各种复杂的现象，如多稳定态、对称性破缺、混沌和涌现。当前的研究领域包括虚拟粒子的效应，[14] 量子纠缠，[15] 惯性质量和引力质量之间的差异（如果有的话），[16] 光速变化，[17] 观察到的宇宙学常数的原因，[18] 以及暗能量的性质。[19][20]

3. 历史

早期的以太理论

　　 零点能量源自关于真空的历史思想。对于亚里士多德来说，真空是 τὸ κενόν，‘空的’；即与物体无关的空间。他认为这个概念违反了基本的物理原则，并主张火、空气、地球和水的元素并非由原子构成，而是连续的。对于原子论者来说，‘空’的概念具有绝对性质：它是存在与不存在的区别。关于真空特性的辩论大多局限于哲学领域，直到文艺复兴时期才开始有所突破，当时奥托·冯·格里克发明了第一个真空泵，科学上可验证的理论才开始出现。人们认为，简单地去除所有气体，就能创造出完全空的空间，这是第一个被普遍接受的真空概念。

　　 然而，到了 19 世纪末，显然即使在抽空的区域中，仍然存在热辐射。以太存在作为真实空无的替代品是当时最流行的理论。根据基于麦克斯韦电动力学的成功电磁以太理论，这种无所不包的以太被赋予了能量，因此与虚无是非常不同的。电磁现象和引力现象能够在空空间中传播，被认为是它们相关的以太是空间本身的一部分。然而，麦克斯韦指出，这些以太在大多数情况下是临时设定的：

　　 “对于那些坚持认为以太作为哲学原则存在的人来说，自然对真空的厌恶是想象一种包围一切的以太的充分理由……以太被发明出来，让行星在其中游动，构成电气大气层和磁气流，传递从身体一部分到另一部分的感觉等等，直到空间被以太填充了三四次。”

　　 此外，1887 年的迈克尔逊–莫雷实验结果是第一次强烈证据表明当时流行的以太理论存在严重缺陷，并启动了最终导致狭义相对论的研究路线，后者完全排除了静止以太的概念。对于当时的科学家来说，似乎可以通过冷却并消除所有辐射或能量来在空间中创造一个真正的真空。由此演变出了第二个实现真正真空的概念：将一个区域的空间冷却至绝对零度温度，然后进行抽空。绝对零度在 19 世纪技术上是无法实现的，因此这一辩论没有得到解决。

第二量子理论

　　 在 1900 年，马克斯·普朗克推导了单个能量辐射体（例如振动的原子单位）平均能量 \(\varepsilon\) 与绝对温度的关系公式： \[ \varepsilon = \frac{h\nu}{e^{h\nu / (kT)} - 1}~ \] 其中，\(h\) 是普朗克常数，\(\nu\) 是频率，\(k\) 是玻尔兹曼常数，\(T\) 是绝对温度。零点能量并未对普朗克的原始定律做出贡献，因为在 1900 年时，普朗克尚不知晓零点能量的存在。

　　 零点能量的概念是由马克斯·普朗克在 1911 年在德国提出的，作为对他在 1900 年提出的原始量子理论中零基态公式的修正项。

　　 在 1912 年，普朗克发表了第一篇关于辐射不连续发射的期刊文章，基于能量的离散量子。他的 “第二量子理论” 中，共振器连续吸收能量，但仅当它们达到相空间的有限单元边界时，才会以离散的能量量子发射能量，其中它们的能量成为 \(h\nu\) 的整数倍。这一理论促使普朗克得出了新的辐射定律，但在这个版本中，能量共振器具有零点能量，即共振器能够取的最小平均能量。普朗克的辐射方程包含一个残余能量因子 \(\frac{h\nu}{2}\) 作为额外项，这个项依赖于频率 \(\nu\)，且大于零（其中 \(h\) 是普朗克常数）。因此，普遍认为 “普朗克方程标志着零点能量概念的诞生”。在 1911 到 1913 年间的一系列论文中，[29]普朗克发现了振荡器的平均能量为： \[ \varepsilon = \frac{h\nu}{2} + \frac{h\nu}{e^{h\nu / (kT)} - 1}~ \]

　　 不久，零点能量的概念引起了阿尔伯特·爱因斯坦及其助手奥托·斯特恩的关注。[31] 他们在 1913 年发表了一篇论文，试图通过计算氢气的比热并与实验数据进行比较来证明零点能量的存在。然而，在他们认为自己成功之后，他们很快撤回了对这一理论的支持，因为他们发现普朗克的第二理论可能并不适用于他们的例子。在同年的一封信中，爱因斯坦向保罗·艾伦费斯特声明，零点能量 “死得像钉子一样”。[32] 零点能量也被彼得·德拜提及，[33] 他指出，即使温度接近绝对零度，晶格中原子的零点能量也会导致 X 射线衍射辐射强度的降低。1916 年，瓦尔特·能斯特提出，空旷的空间充满了零点电磁辐射。[34] 随着广义相对论的发展，爱因斯坦发现真空的能量密度有助于产生一个宇宙常数，以便得到他场方程的静态解；空旷空间或真空可以具有某种内在能量的观点重新出现了。爱因斯坦在 1920 年表示：

　　 有一个强有力的论点支持以太假说。否认以太最终意味着假设空旷空间没有任何物理性质。力学的基本事实与这种观点并不和谐……根据广义相对论，空间是赋予物理性质的；因此，在这个意义上，存在一个以太。根据广义相对论，没有以太的空间是不可思议的；因为在这样的空间中，不仅没有光的传播，而且没有时间和空间的标准存在（即测量杆和时钟），因此也就没有物理意义上的时空间隔。但是，这个以太不能被看作是具有可追溯时间的物质特性，也不能应用于可追踪的部分。运动的概念不能应用于它。[35][36]

　　 Kurt Bennewitz 和 Francis Simon（1923 年），他们在沃尔特·能斯特（Walther Nernst）位于柏林的实验室工作，研究了低温下化学物质的熔化过程。他们计算了氢气、氩气和水银的熔点，并得出结论，认为这些结果为零点能提供了证据。此外，他们还正确地提出（后来由西蒙（1934 年）验证）这一量是导致氦气即使在绝对零度下也难以固化的原因。1924 年，罗伯特·穆立肯（Robert Mulliken）通过比较 10BO 和 11BO 的带谱，提供了分子振动的零点能的直接证据：如果没有零点能，不同电子能级基态的振动频率的同位素差异应该会消失，这与观察到的谱线相矛盾。仅仅一年后的 1925 年，随着在维尔纳·海森堡的文章《量子理论对运动学和力学关系的重新解释》中矩阵力学的发展，零点能从量子力学中得到了推导。

　　 1913 年，尼尔斯·玻尔（Niels Bohr）提出了现在被称为玻尔模型的原子模型，但尽管如此，为什么电子不会坠入原子核依然是一个谜。根据经典理论，考虑到加速电荷通过辐射损失能量，意味着电子应该会螺旋式地坠入原子核，原子也不应该是稳定的。这个经典力学的问题在 1915 年被詹姆斯·霍普伍德·吉恩斯（James Hopwood Jeans）总结得很好：“假设力学定律 \(\frac{1}{r^2}\) 在 r 趋近于零时仍然成立，将会是一个非常真实的困难。因为两电荷在零距离时的相互作用力将是无限大的；我们应该看到异号电荷不断相互吸引，且一旦相遇，没有力会使它们进一步收缩或无限减小。” 这一难题的解决出现在 1926 年，当时厄尔温·薛定谔（Erwin Schrödinger）提出了薛定谔方程。该方程解释了这样一个新的非经典事实：当电子被限制靠近原子核时，它必然会拥有很大的动能，因此最小的总能量（动能加势能）实际上会出现在某个正的距离上，而不是零距离；换句话说，零点能对于原子稳定性至关重要。

量子场论及其发展

　　 1926 年，帕斯夸尔·乔丹（Pascual Jordan）首次尝试对电磁场进行量子化。在与马克斯·玻恩（Max Born）和维尔纳·海森堡（Werner Heisenberg）合作的论文中，他将腔体内的场视为量子谐振子的叠加。在计算中，他发现，除了振荡器的 “热能” 之外，还必须存在一个无限的零点能项。他得出了与爱因斯坦在 1909 年得到的相同的波动公式。然而，乔丹并不认为他的无限零点能项是 “真实的”，他写信给爱因斯坦说：“这只是计算中的一个量，没有直接的物理意义”。乔丹找到了一种方法来去除这个无限项，并于 1928 年与泡利（Pauli）共同发表了一篇论文，进行了一次被称为 “量子场论中的第一次无限减法或重正化” 的操作。

　　 基于海森堡等人的工作，保罗·狄拉克在 1927 年提出的辐射的发射与吸收理论[54] 是量子辐射理论的首次应用。狄拉克的工作被认为对新兴的量子力学领域至关重要；它直接处理了 “粒子” 实际是如何被创造出来的过程：自发辐射。[55] 狄拉克将电磁场的量子化描述为一个由谐振子组成的集合，并引入了粒子的产生和湮灭算符的概念。该理论表明，自发辐射依赖于电磁场的零点能波动才能开始。[56][57] 在一个光子被湮灭（吸收）的过程中，光子可以被看作是进入了真空态。类似地，当光子被创造（发射）时，偶尔可以认为光子是从真空态过渡到一个实际存在的状态。用狄拉克的话来说：[54]

　　 光量子有一个特性，即它似乎在其某些驻定状态下不存在，即零状态，其中它的动量，因此也它的能量，都是零。当一个光量子被吸收时，可以认为它跳入了这个零状态，而当一个光量子被发射时，可以认为它是从零状态跳到一个它在物理上显现出来的状态，从而看起来像是被创造出来了。由于没有限制可以这样创造的光量子的数量，我们必须假设零状态中存在无限多的光量子...

　　 当代物理学家在被问及自发辐射的物理解释时，通常会引用电磁场的零点能。这一观点由维克多·韦斯科普夫（Victor Weisskopf）在 1935 年提出并推广：[58]

　　 从量子理论中可以推导出所谓零点振荡的存在；例如，每个振荡器在其最低状态下并不完全静止，而是始终围绕其平衡位置运动。因此电磁振荡也不可能完全停止。因此，电磁场的量子特性导致了场强在最低能量状态下的零点振荡，在这种状态下，空间中没有光量子... 零点振荡作用在电子上与普通的电振荡相同。它们可以改变电子的本征状态，但仅限于过渡到最低能量的状态，因为空旷的空间只能带走能量，而不能给予能量。通过这种方式，自发辐射作为这些与零点振荡相对应的独特场强存在的结果而产生。因此，自发辐射是由空旷空间的零点振荡引发的光量子辐射。

　　 这一观点后来得到了西奥多·韦尔顿（Theodore Welton，1948 年）的支持，[59] 他认为自发辐射 “可以被视为在波动场的作用下发生的强迫辐射”。这一新理论，狄拉克称之为量子电动力学（QED），预言了即使在没有源的情况下，也存在波动的零点场或 “真空场”。

　　 在 1940 年代，微波技术的改进使得能够更精确地测量氢原子能级的跃迁，现在称为兰姆位移（Lamb shift），[60] 并测量了电子的磁矩。[61] 这些实验结果与狄拉克理论之间的差异促使了将重正化引入 QED 以处理零点能的无限大的问题。重正化最初由汉斯·克拉梅尔（Hans Kramers）[62] 和维克多·韦斯科普夫（1936 年）[63] 提出，并在 1947 年由汉斯·贝特（Hans Bethe）首次成功地应用于计算兰姆位移的有限值。[64] 关于自发辐射，这些效应可以部分通过与零点场的相互作用来理解。[65][11] 但由于重正化能够从计算中去除一些零点能的无限大，并不是所有的物理学家都愿意给零点能赋予任何物理意义，而是将其视为一个数学工件，认为它可能在某一天被消除。在沃尔夫冈·泡利 1945 年的诺贝尔讲座[66]中，他明确表示反对零点能的观点，称 “显然，这个零点能没有物理现实”。

　　 1948 年，亨德里克·卡西米尔（Hendrik Casimir）证明了零点场的一个后果是，在两个无电荷、完全导电的平行板之间会产生吸引力，这就是所谓的卡西米尔效应。当时，卡西米尔正在研究胶体溶液的性质。胶体溶液是含有微米级颗粒的液体基质，如油漆和蛋黄酱。这些溶液的性质由范德华力决定——范德华力是一种存在于中性原子和分子之间的短程吸引力。卡西米尔的一位同事，西奥·欧尔贝克（Theo Overbeek）意识到，当时用于解释范德华力的理论，由弗里茨·伦敦（Fritz London）在 1930 年发展出来的，并未能正确解释胶体实验数据。因此，欧尔贝克要求卡西米尔研究这个问题。在与迪尔克·波尔德（Dirk Polder）合作时，卡西米尔发现，只有考虑光传播有限速度的事实，才能正确描述两个中性分子之间的相互作用。不久之后，在与玻尔（Bohr）讨论零点能的过程中，卡西米尔注意到，这一结果可以用真空波动来解释。他开始思考，如果有两面镜子——而不是两分子——在真空中面对面，会发生什么。正是这项工作导致了他对反射板之间吸引力的预测。卡西米尔和波尔德的工作为范德华力和卡西米尔力的统一理论铺平了道路，并在两种现象之间建立了平滑的过渡。利夫希茨（Lifshitz）在 1956 年（1956 年）做出了相关工作，针对平行介电板的情况完成了这一理论的统一。范德华力和卡西米尔力的统称为色散力，因为它们都是由偶极矩算符的色散引起的。相对论性力的作用在约百纳米的尺度上变得主导。

　　 1951 年，赫伯特·卡伦（Herbert Callen）和西奥多·韦尔顿（Theodore Welton）证明了量子涨落-耗散定理（FDT），该定理最初由奈奎斯特（Nyquist）在 1928 年以经典形式提出，用于解释电路中的约翰逊噪声。涨落-耗散定理表明，当某物耗散能量时，以一种有效的不可逆方式，连接的热浴也必须发生涨落。涨落和耗散是密不可分的，二者不可分离。FDT 的意义在于，真空可以被视为与耗散力耦合的热浴，因此能量可以部分地从真空中提取出来，用于潜在的有用工作。FDT 已在某些量子非经典条件下被实验验证为真实。

　　 1963 年，杰恩斯-卡明斯模型（Jaynes-Cummings model）被提出，描述了二能级原子与量子场模式（即真空）在光学腔中的相互作用。该模型给出了直觉上不容易理解的预测，例如原子的自发辐射可能被有效频率（拉比频率）驱动。在 1970 年代，实验开始测试量子光学的各个方面，结果表明，原子的自发辐射速率可以通过反射表面进行调控。最初，这些结果在一些领域中被怀疑：人们认为自发辐射速率无法修改，因为，究竟原子如何通过发射光子 “看见” 它的环境，而一开始就需要发射光子？这些实验催生了腔量子电动力学（CQED），即研究镜子和腔体对辐射修正的影响。自发辐射可以被抑制（或 “抑制”）或放大。放大的现象最早由帕塞尔（Purcell）在 1946 年预测（帕塞尔效应），并已被实验验证。部分而言，这种现象可以通过真空场对原子的作用来理解。

4. 不确定性原理

　　 零点能与海森堡不确定性原理密切相关。粗略地说，不确定性原理表明，互补变量（例如粒子的位置和动量，或场的值和在空间中的导数）不能通过任何给定的量子态同时精确指定。特别地，不可能存在一个系统处于其势阱底部静止不动的状态，因为在这种状态下，位置和动量将会被完全确定，并且可以达到任意高的精度。因此，系统的最低能量状态（基态）必须具有一个位置和动量的分布，这个分布满足不确定性原理，这意味着其能量必须大于势阱的最低点。

　　 在势阱底部附近，通用系统的哈密顿量（给出其能量的量子力学算符）可以近似为量子谐振子： \[ {\hat {H}} = V_0 + \frac{1}{2}k\left({\hat {x}} - x_0\right)^2 + \frac{1}{2m}{\hat {p}}^2~ \] 其中，\(V_0\) 是经典势阱的最小值。

　　 不确定性原理告诉我们： \[ \sqrt{\langle \left({\hat {x}} - x_0\right)^2 \rangle} \sqrt{\langle {\hat {p}}^2 \rangle} \geq \frac{\hbar}{2}~ \] 这使得上面动能和势能项的期望值满足： \[ \langle \frac{1}{2}k\left({\hat {x}} - x_0\right)^2 \rangle \langle \frac{1}{2m}{\hat {p}}^2 \rangle \geq \left( \frac{\hbar}{4} \right)^2 \frac{k}{m}~ \] 因此，能量的期望值至少为： \[ \langle {\hat {H}} \rangle \geq V_0 + \frac{\hbar}{2} \sqrt{\frac{k}{m}} = V_0 + \frac{\hbar \omega}{2}~ \] 其中，\(\omega = \sqrt{k/m}\) 是系统振荡的角频率。

　　 更深入的处理表明，基态的能量实际上会饱和这个界限，并且是精确的：\(E_0 = V_0 + \frac{\hbar \omega}{2}\) 这需要解系统的基态。

5. 原子物理学

　　 量子谐振子的概念及其相关的能量可以应用于原子或亚原子粒子。在普通的原子物理学中，零点能是与系统基态相关的能量。专业物理文献通常使用角频率（ω）来测量频率，如上文所示的ν，且定义为ω = 2πν。这导致了一种约定，使用带有横线的普朗克常数（ħ）来表示数量 \( \frac{h}{2\pi} \)。用这种方式，零点能的一个例子是上面的 \( E = \frac{\hbar \omega}{2} \)，它与量子谐振子的基态相关。在量子力学中，零点能是系统在基态下哈密顿量的期望值。

　　 如果存在多个基态，则称这些基态是简并的。许多系统具有简并的基态。简并性发生在存在一个酉算符，该算符在基态上非平凡地作用并与系统的哈密顿量对易时。

　　 根据热力学第三定律，处于绝对零度的系统存在于其基态；因此，它的熵由基态的简并度决定。许多系统，如完美的晶格，具有唯一的基态，因此在绝对零度下熵为零。对于表现出负温度的系统，也有可能最高激发态在绝对零度下存在。

　　 一维势阱中粒子的基态波函数是一个半周期的正弦波，在势阱的两个边缘处为零。粒子的能量由以下公式给出： \[ E = \frac{h^2 n^2}{8mL^2}~ \] 其中，\( h \) 是普朗克常数，\( m \) 是粒子的质量，\( n \) 是能级（\( n = 1 \) 对应基态能量），\( L \) 是势阱的宽度。

6. 量子场论

　　 在量子场论（QFT）中，“空” 空间的结构被想象成由场组成，空间和时间中的每一点都可以视为一个量子谐振子，相邻的振荡子相互作用。根据 QFT，宇宙由物质场组成，其量子是费米子（如电子和夸克）；力场，其量子是玻色子（即光子和胶子）；以及一个希格斯场，其量子是希格斯玻色子。物质场和力场都具有零点能量。一个相关的术语是零点场（ZPF），它是特定场的最低能量态。真空可以被视为不是空的空间，而是所有零点场的组合。

　　 在 QFT 中，真空态的零点能量被称为真空能量，而哈密顿量的平均期望值被称为真空期望值（也叫凝聚态或简写为 VEV）。量子电动力学（QED）真空是处理量子电动力学（例如光子、电子与真空之间的电磁相互作用）的真空态的一部分，而量子色动力学（QCD）真空则处理量子色动力学（例如夸克、胶子与真空之间的色荷相互作用）。最近的实验支持这样一个观点：粒子本身可以被看作是潜在量子真空的激发态，并且物质的所有属性仅仅是由于与零点场相互作用而产生的真空波动。

　　 空间中的每一点都贡献 \( E = \frac{\hbar \omega}{2} \)，这导致在任何有限体积内计算出无限的零点能量；这也是需要重整化才能使量子场论具有实际意义的一个原因。在宇宙学中，真空能量是解释宇宙学常数和暗能量来源的一个可能解释。

　　 科学家们对于真空中包含多少能量并没有达成一致。量子力学要求能量大，如保罗·狄拉克所宣称，它像一个能量海洋。其他专攻广义相对论的科学家要求能量足够小，以便空间的曲率与观测到的天文学现象相符。海森堡不确定性原理允许能量足够大，以促使量子行为在短暂时间内发生，即使平均能量足够小，满足相对论和平坦空间的要求。为了应对这种分歧，真空能量被描述为一种具有正负能量的虚拟能量势。

　　 在量子扰动理论中，有时会说，一环和多环费曼图对基本粒子传播子的贡献就是真空波动或零点能量对粒子质量的贡献。

量子电动力学真空

　　 最古老且最著名的量子化力场是电磁场。麦克斯韦方程已被量子电动力学（QED）所取代。通过考虑源自量子电动力学的零点能，可以获得对零点能的特征性理解，这种零点能不仅仅通过电磁相互作用产生，而且在所有量子场论中都有出现。

　　 重新定义能量的零点

　　 在电磁场的量子理论中，经典的波振幅α和α*被运算符 a 和 a†取代，满足以下关系： \[ [a, a^{\dagger}] = 1~ \] 经典表达式中出现的量|α|²，在量子理论中被光子数算符 a†a 所替代。事实上： \[ [a, a^{\dagger}a] \neq 1~ \] 这意味着量子理论不允许辐射场的状态，其中光子数和场振幅可以精确地定义，也就是说，我们无法为 a†a 和 a 同时找到特征态。场的波动性和粒子属性的调和通过将概率振幅与经典模式相联系来完成。场模式的计算是完全经典的问题，而场的量子特性则由与这些经典模式相关联的模式 “振幅” a†和 a 承载。

　　 场的零点能形式上来源于 a 和 a†的不对易性。这对任何谐振子都成立：零点能 \(\frac{\hbar \omega}{2}\) 出现在我们写出哈密顿量时： \[ H_{cl} = \frac{p^2}{2m} + \frac{1}{2}m\omega^2 q^2 = \frac{1}{2}\hbar \omega (a a^{\dagger} + a^{\dagger} a) = \hbar \omega \left(a^{\dagger} a + \frac{1}{2}\right)~ \] 通常有一种观点认为整个宇宙完全浸泡在零点电磁场中，因此它只能对期望值添加一个常数量。因此，物理测量将只揭示偏离真空状态的变化。因此，通过重新定义能量的零点，或者认为它是常数且因此对海森堡运动方程没有影响，可以将零点能从哈密顿量中去掉。因此，我们可以通过法定声明，假设基态能量为零，举例如下，场哈密顿量可以被替换为： \[ H_F - \langle 0 | H_F | 0 \rangle = \frac{1}{2} \hbar \omega (a a^{\dagger} + a^{\dagger} a) - \frac{1}{2} \hbar \omega = \hbar \omega (a^{\dagger} a + \frac{1}{2}) - \frac{1}{2} \hbar \omega = \hbar \omega a^{\dagger} a~ \] 而不会影响理论的任何物理预测。新的哈密顿量被称为正规排列（或维克排列），用双点符号表示。正规排列的哈密顿量表示为：\( :H_F: \)，即： \[ H_F: \equiv \hbar \omega (a a^{\dagger} + a^{\dagger} a) \equiv \hbar \omega a^{\dagger} a~ \] 换句话说，在正规排列符号内，我们可以交换 a 和 a†。由于零点能与 a 和 a†的不对易性密切相关，正规排列过程消除了零点场的任何贡献。这在场哈密顿量的情况下尤其合理，因为零点项仅仅添加了一个常数能量，可以通过简单的零点能量重新定义来去除。此外，这个常数能量显然与 a 和 a†对易，因此不会对由海森堡方程描述的量子动力学产生任何影响。

　　 然而，事情并没有那么简单。零点能不能仅通过从哈密顿量中去掉其能量来消除：当我们这么做并求解场算符的海森堡方程时，我们必须包括真空场，它是场算符解的均匀部分。事实上，我们可以证明，真空场对于保持对易子和 QED 的形式一致性至关重要。当我们计算场能量时，除了可能存在的粒子和力的贡献外，还会得到来自真空场本身，即零点场能量的贡献。换句话说，即使我们可能已将零点能从哈密顿量中删除，它依然会重新出现。

　　 自由空间中的电磁场

　　 根据麦克斯韦方程，"自由"场（即没有源的场）的电磁能量可以通过以下公式描述： \[ H_F = \frac{1}{8\pi} \int d^3r \left( \mathbf{E}^2 + \mathbf{B}^2 \right) = \frac{k^2}{2\pi} |\alpha(t)|^2~ \] 我们引入满足赫尔姆霍兹方程的 “模式函数” \( A_0(r) \)： \[ (\nabla^2 + k^2) \mathbf{A}_0(\mathbf{r}) = 0~ \] 其中 \( k = \frac{\omega}{c} \)，并假设它已标准化，使得： \[ \int d^3r \left| \mathbf{A}_0(\mathbf{r}) \right|^2 = 1~ \] 我们希望对自由空间的电磁能量进行 “量子化”，以适应多模式场。自由空间的场强度应与位置无关，因此对于每个场模式，\(|A_0(r)|^2\) 应与 \(r\) 无关。满足这些条件的模式函数为： \[ \mathbf{A}_0(\mathbf{r}) = e_{\mathbf{k}} e^{i \mathbf{k} \cdot \mathbf{r}}~ \] 其中 \( \mathbf{k} \cdot e_{\mathbf{k}} = 0 \)，以便在我们所使用的库仑规中满足横向条件 \( \nabla \cdot A(r,t) = 0 \)。

　　 为了实现所需的标准化，我们假设空间被分割为体积为 \( V = L^3 \) 的立方体，并对场施加周期性边界条件： \[ \mathbf{A}(x+L, y+L, z+L, t) = \mathbf{A}(x, y, z, t)~ \] 或者等效地： \[ (k_x, k_y, k_z) = \frac{2\pi}{L}(n_x, n_y, n_z)~ \] 其中 \( n \) 可以取任何整数值。这样，我们可以在任意一个虚拟立方体中考虑场，并定义模式函数： \[ \mathbf{A}_{\mathbf{k}}(\mathbf{r}) = \frac{1}{\sqrt{V}} e_{\mathbf{k}} e^{i \mathbf{k} \cdot \mathbf{r}}~ \] 该函数满足赫尔姆霍兹方程、横向条件以及 “盒子标准化”： \[ \int_V d^3r \left|\mathbf{A}_{\mathbf{k}}(\mathbf{r})\right|^2 = 1~ \] 其中，\(\mathbf{e}_k\) 被选为单位矢量，指定场模式的极化方向。条件 \( \mathbf{k} \cdot \mathbf{e}_k = 0 \) 意味着存在两种独立的选择 \(\mathbf{e}_k\)，我们称之为 \(\mathbf{e}_{k1}\) 和 \(\mathbf{e}_{k2}\)，它们满足 \(\mathbf{e}_{k1} \cdot \mathbf{e}_{k2} = 0\) 和 \( \mathbf{e}_{k1}^2 = \mathbf{e}_{k2}^2 = 1 \)。因此，我们定义模式函数为： \[ \mathbf{A}_{\mathbf{k} \lambda}(\mathbf{r}) = \frac{1}{\sqrt{V}} \mathbf{e}_{\mathbf{k} \lambda} e^{i \mathbf{k} \cdot \mathbf{r}}, \quad \lambda = \begin{cases}1 \\ 2\end{cases}~ \] 在此基础上，电磁场的矢势可以表示为： \[ \mathbf{A}_{\mathbf{k} \lambda}(\mathbf{r}, t) = \sqrt{\frac{2\pi \hbar c^2}{\omega_k V}} \left[ a_{\mathbf{k} \lambda}(0) e^{i \mathbf{k} \cdot \mathbf{r}} + a_{\mathbf{k} \lambda}^\dagger(0) e^{-i \mathbf{k} \cdot \mathbf{r}} \right] \mathbf{e}_{\mathbf{k} \lambda}~ \] 或者 \[ \mathbf{A}_{\mathbf{k} \lambda}(\mathbf{r}, t) = \sqrt{\frac{2\pi \hbar c^2}{\omega_k V}} \left[ a_{\mathbf{k} \lambda}(0) e^{-i(\omega_k t - \mathbf{k} \cdot \mathbf{r})} + a_{\mathbf{k} \lambda}^\dagger(0) e^{i(\omega_k t - \mathbf{k} \cdot \mathbf{r})} \right]~ \] 其中 \(\omega_k = k c\)，\(a_{\mathbf{k} \lambda}\) 和 \(a_{\mathbf{k} \lambda}^\dagger\) 是对应波矢 \(\mathbf{k}\) 和极化 \(\lambda\) 的光子湮灭和产生算符。这个式子给出了平面波模式下的电磁场矢势。通过对波矢 \((k_x, k_y, k_z)\) 的约束，表明存在无限多种这样的模式。麦克斯韦方程的线性特性使得我们可以写出自由空间中的总矢势： \[ \mathbf{A}(\mathbf{r}, t) = \sum_{\mathbf{k} \lambda} \sqrt{\frac{2\pi \hbar c^2}{\omega_k V}} \left[ a_{\mathbf{k} \lambda}(0) e^{i \mathbf{k} \cdot \mathbf{r}} + a_{\mathbf{k} \lambda}^\dagger(0) e^{-i \mathbf{k} \cdot \mathbf{r}} \right] \mathbf{e}_{\mathbf{k} \lambda}~ \] 使用如下的正交条件： \[ \int_V d^3r \mathbf{A}_{\mathbf{k} \lambda}(\mathbf{r}) \cdot \mathbf{A}_{\mathbf{k'} \lambda'}^*(\mathbf{r}) = \delta_{\mathbf{k}, \mathbf{k'}}^3 \delta_{\lambda, \lambda'}~ \] 我们得到场的哈密顿量为： \[ H_F = \sum_{\mathbf{k} \lambda} \hbar \omega_k \left( a_{\mathbf{k} \lambda}^\dagger a_{\mathbf{k} \lambda} + \frac{1}{2} \right)~ \] 这是一个无限数量的独立简谐振子的哈密顿量。因此，场的不同模式是独立的，并且满足以下对易关系： \[ [a_{\mathbf{k} \lambda}(t), a_{\mathbf{k'} \lambda'}^\dagger(t)] = \delta_{\mathbf{k}, \mathbf{k'}}^3 \delta_{\lambda, \lambda'}~ \] \[ [a_{\mathbf{k} \lambda}(t), a_{\mathbf{k'} \lambda'}(t)] = [a_{\mathbf{k} \lambda}^\dagger(t), a_{\mathbf{k'} \lambda'}^\dagger(t)] = 0~ \] 显然，哈密顿量 \( H_F \) 的最小本征值是： \[ \sum_{\mathbf{k} \lambda} \frac{1}{2} \hbar \omega_k~ \] 这个状态描述了真空的零点能量。这个求和看起来是发散的，实际上是高度发散的，因为当加入密度因子： \[ \frac{8\pi v^2 dv}{c^3} V~ \] 时，求和变成了一个积分： \[ \frac{4\pi h V}{c^3} \int v^3 dv~ \] 对于大的 \( v \) 值，它的发散度是与 \( v^4 \) 成比例的。

　　 这里有两个独立的问题需要考虑。首先，发散是否是真实的，使得零点能量确实是无限的？如果我们考虑体积 \(V\) 被完全导电的墙壁包围，那么很高的频率只能通过越来越完美的导电性来容纳。实际上，并没有可能的方法来容纳这些高频模式。这些模式在我们的盒子中不会是静止的，因此不能计算在静止能量的内容中。从这个物理角度来看，上述的求和应该只延伸到那些是可数的频率，因此一个截止能量是非常合理的。然而，在 “宇宙” 尺度上，必须包括广义相对论的问题。假设这些盒子可以被复制、拼接并通过弯曲时空很好地闭合。那么，运行波的精确条件可能是可能的。然而，这些非常高频的量子仍然无法被容纳。根据约翰·惠勒的 “几何子”（geons），这些量子将会泄漏出系统。所以再次地，截止是允许的，甚至几乎是必要的。这里的问题变成了一致性的问题，因为这些非常高能的量子将作为质量源，开始弯曲几何。

　　 这引出了第二个问题。无论发散与否，有限还是无限，零点能量是否具有任何物理意义？在所有实际计算中，通常都鼓励忽略整个零点能量。这样做的原因是能量通常不是由一个任意的数据点定义的，而是由数据点之间的变化来定义的，因此加上或减去一个常数（即使是无限的）应该是允许的。然而，这并不是全部，实际上能量并不是那么任意地定义的：在广义相对论中，时空曲率的来源就是能量内容，在那里，能量的绝对量具有真实的物理意义。没有所谓的任意加法常数和场能量密度。能量密度弯曲空间，能量密度的增加会导致曲率的增加。此外，零点能量密度还有其他物理后果，例如卡西米尔效应、兰姆位移的贡献，或者电子的异常磁矩，显然它不仅仅是一个可以被抵消的数学常数或伪影。

　　 量子电动力学中真空场的必要性

　　 自由” 电磁场的真空态（即没有源的情况下）被定义为基态，在该基态中，对于所有模式（\(k, \lambda\)），\(n_{k\lambda} = 0\)。与场的所有静态态一样，真空态是哈密顿量的本征态，但不是电场和磁场算符的本征态。因此，在真空态中，电场和磁场没有确定的值。我们可以想象它们围绕着其零的平均值波动。

　　 在一个光子湮灭（吸收）的过程中，我们可以认为光子做了从一个状态过渡到真空态。类似地，当一个光子被创造（发射）时，我们有时可以想象该光子是从真空态过渡出来的。[54] 例如，一个原子可以被认为是通过发射和再吸收来自真空的 “虚拟光子” 来 “着装” 的。由 \(\sum_{k\lambda} \frac{\hbar \omega_k}{2}\) 描述的真空态能量是无限的。我们可以进行替换： \[ \sum_{k\lambda} \longrightarrow \sum_{\lambda} \left(\frac{1}{2\pi}\right)^3 \int d^3k = \frac{V}{8\pi^3} \sum_{\lambda} \int d^3k~ \] 零点能量密度为： \[ \frac{1}{V} \sum_{k\lambda} \frac{1}{2} \hbar \omega_k = \frac{2}{8\pi^3} \int d^3k \frac{1}{2} \hbar \omega_k = \frac{4\pi}{4\pi^3} \int dk\, k^2 \left(\frac{1}{2} \hbar \omega_k \right) = \frac{\hbar}{2\pi^2 c^3} \int d\omega \, \omega^3~ \] 换句话说，真空场的谱能量密度为： \[ \rho_0(\omega) = \frac{\hbar \omega^3}{2\pi^2 c^3}~ \] 因此，频率范围从 \(\omega_1\) 到 \(\omega_2\) 的零点能量密度为： \[ \int_{\omega_1}^{\omega_2} d\omega \, \rho_0(\omega) = \frac{\hbar}{8\pi^2 c^3} \left(\omega_2^4 - \omega_1^4\right)~ \] 即使在相对狭窄的 “低频” 频段，这个值也可能很大。例如，在光学区域从 400 到 700 纳米的范围内，上述方程给出的结果大约是 220 erg/cm³。

　　 我们在上面的部分中展示了，可以通过常规排序方法将零点能量从哈密顿量中消除。然而，这种消除并不意味着真空场已经不重要或没有物理意义。为了说明这一点，我们考虑真空中的一个线性偶极子振荡器。该振荡器及其相互作用的场的哈密顿量为： \[ H = \frac{1}{2m} \left( \mathbf{p} - \frac{e}{c} \mathbf{A} \right)^2 + \frac{1}{2} m \omega_0^2 \mathbf{x}^2 + H_F~ \] 这个哈密顿量与相应的经典哈密顿量形式相同，且振荡器和场的海森堡运动方程在形式上与经典方程相同。例如，振荡器的坐标 \( \mathbf{x} \) 和规范动量 \( \mathbf{p} = m \dot{\mathbf{x}} + \frac{eA}{c} \) 的海森堡运动方程为： \[ \dot{\mathbf{x}} = (i\hbar)^{-1} [\mathbf{x}, H] = \frac{1}{m} \left( \mathbf{p} - \frac{e}{c} \mathbf{A} \right)~ \] \[ = \frac{1}{2} \nabla \left( \mathbf{p} - \frac{e}{c} \mathbf{A} \right)^2 - m \omega_0^2 \dot{\mathbf{x}}~ \] \[ \dot{\mathbf{p}} = (i\hbar)^{-1} [\mathbf{p}, H] = -\frac{1}{m} \left[ \left( \mathbf{p} - \frac{e}{c} \mathbf{A} \right) \cdot \nabla \right] \left( -\frac{e}{c} \mathbf{A} \right) - \frac{1}{m} \left( \mathbf{p} - \frac{e}{c} \mathbf{A} \right) \times \nabla \times \left( -\frac{e}{c} \mathbf{A} \right) - m \omega_0^2 \dot{\mathbf{x}}~ \] \[ = \frac{e}{c} (\dot{\mathbf{x}} \cdot \nabla) \mathbf{A} + \frac{e}{c} \dot{\mathbf{x}} \times \mathbf{B} - m \omega_0^2 \dot{\mathbf{x}}~ \] 或者： \[ m \ddot{\mathbf{x}} = \dot{\mathbf{p}} - \frac{e}{c} \dot{\mathbf{A}} = -\frac{e}{c} \left[ \dot{\mathbf{A}} - (\dot{\mathbf{x}} \cdot \nabla) \mathbf{A} \right] + \frac{e}{c} \dot{\mathbf{x}} \times \mathbf{B} - m \omega_0^2 \mathbf{x}~ \] \[ = e \mathbf{E} + \frac{e}{c} \dot{\mathbf{x}} \times \mathbf{B} - m \omega_0^2 \mathbf{x}~ \] 由于在运动电荷的参考系中，矢量势的变化率由对流导数给出： \[ \dot{\mathbf{A}} = \frac{\partial \mathbf{A}}{\partial t} + (\dot{\mathbf{x}} \cdot \nabla) \mathbf{A}~ \] 对于非相对论性运动，我们可以忽略磁力，并将 \( m \ddot{\mathbf{x}} \) 的表达式替换为： \[ \ddot{\mathbf{x}} + \omega_0^2 \mathbf{x} \approx \frac{e}{m} \mathbf{E} \approx \sum_{\mathbf{k} \lambda} \sqrt{\frac{2\pi \hbar \omega_k}{V}} \left[a_{\mathbf{k} \lambda}(t) + a_{\mathbf{k} \lambda}^{\dagger}(t)\right] e_{\mathbf{k} \lambda}~ \] 在上述过程中，我们做了电偶极子近似，即忽略了场的空间依赖性。\( a_{k\lambda} \) 的海森堡方程可以类似地从哈密顿量中推导出来，得到： \[ \dot{a}_{\mathbf{k} \lambda} = i \omega_k a_{\mathbf{k} \lambda} + ie \sqrt{\frac{2\pi}{\hbar \omega_k V}} \dot{\mathbf{x}} \cdot e_{\mathbf{k} \lambda}~ \] 这是在电偶极子近似下的结果。

　　 在推导 \( x \)、\( p \) 和 \( a_{k\lambda} \) 的方程时，我们利用了粒子和场算符在等时刻对易的事实。这是因为假设粒子和场算符在某一时刻（例如，\( t = 0 \)）对易，而在此时刻假设物质场的解释开始。再加上海森堡图像算符 \( A(t) \) 随时间演化的事实，即：\(A(t) = U^{\dagger}(t) A(0) U(t)\) 其中，时间演化算符 \( U(t) \) 满足： \[ i\hbar \dot{U} = H U, \quad U^{\dagger}(t) = U^{-1}(t), \quad U(0) = 1~ \] 另外，我们也可以认为这些算符必须对易，才能从哈密顿量中得到正确的运动方程，就像经典理论中对应的泊松括号必须为零，以生成正确的哈密顿方程一样。场方程的正规解为： \[ a_{k\lambda}(t) = a_{k\lambda}(0) e^{-i\omega_k t} + ie \sqrt{\frac{2\pi}{\hbar \omega_k V}} \int_0^t dt' e_{k\lambda} \cdot \dot{\mathbf{x}}(t') e^{i\omega_k(t' - t)}~ \] 因此，\( \ddot{a}_{k\lambda} \) 的方程可以写作： \[ \ddot{\mathbf{x}} + \omega_0^2 \mathbf{x} = \frac{e}{m} \mathbf{E}_0(t) + \frac{e}{m} \mathbf{E}_{RR}(t)~ \] 其中，\( \mathbf{E}_0(t) \) 为： \[ \mathbf{E}_0(t) = i \sum_{\mathbf{k} \lambda} \sqrt{\frac{2\pi \hbar \omega_k}{V}} \left[ a_{k\lambda}(0) e^{-i\omega_k t} - a_{k\lambda}^{\dagger}(0) e^{i\omega_k t} \right] e_{k\lambda}~ \] 而 \( \mathbf{E}_{RR}(t) \) 为： \[ \mathbf{E}_{RR}(t) = -\frac{4\pi e}{V} \sum_{\mathbf{k} \lambda} \int_0^t dt' \left[ e_{\mathbf{k} \lambda} \cdot \dot{\mathbf{x}}(t') \right] \cos \omega_k (t' - t)~ \] 可以证明，在辐射反应场中，如果质量 \( m \) 被视为 “观测” 质量，则可以取： \[ \mathbf{E}_{RR}(t) = \frac{2e}{3c^3} \ddot{\mathbf{x}}~ \] 作用在偶极子上的总场有两部分：\( E_0(t) \) 和 \( E_{RR}(t) \)。\( E_0(t) \) 是作用在偶极子上的自由场或零点场。它是麦克斯韦方程的均匀解，即场在偶极子位置处满足的波动方程的解： \[ \left[ \nabla^2 - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right] \mathbf{E} = 0~ \] 这个方程由（无源）真空中的场满足。因此，\( E_0(t) \) 通常被称为 “真空场”，尽管它当然是一个海森堡图像算符，作用于在 \( t = 0 \) 时适当的场态。\( E_{RR}(t) \) 是源场，即由偶极子产生并作用在偶极子上的场。

　　 利用上述 \( E_{RR}(t) \) 的方程，我们得到海森堡图像算符 \( \mathbf{x}(t) \) 的方程，它在形式上与线性偶极子振荡器的经典方程相同： \[ \ddot{\mathbf{x}} + \omega_0^2 \mathbf{x} - \tau \overset{...}{\mathbf{x}} = \frac{e}{m} \mathbf{E}_0(t)~ \] 其中 \( \tau = \frac{2e^2}{3mc^3} \)。在此情况下，我们考虑了一个处于真空中的偶极子，没有任何 “外部” 场作用在其上。上述方程中 “外部场” 的角色由真空电场 \( E_0(t) \) 作用在偶极子上来扮演。

　　 从经典物理的角度看，处于真空中的偶极子不会受到任何 “外部” 场的作用：如果除了偶极子本身没有其他源，那么作用在偶极子上的唯一场就是它自身的辐射反应场。然而，在量子理论中，总是存在一个 “外部” 场，即无源场或真空场 \( E_0(t) \)。

　　 根据我们之前的 \( a_{k\lambda}(t) \) 方程，自由场是 \( t = 0 \) 时唯一存在的场，即偶极子与场之间的相互作用在这个时刻 “开启”。因此，偶极子-场系统在 \( t = 0 \) 时的态矢量是： \[ |\Psi \rangle = |{\text{vac}}\rangle |\psi_D \rangle~ \] 其中 \( |{\text{vac}}\rangle \) 是场的真空态，\( |\psi_D \rangle \) 是偶极子振荡器的初态。因此，自由场的期望值在所有时间都等于零： \[ \langle \mathbf{E}_0(t) \rangle = \langle \Psi | \mathbf{E}_0(t) | \Psi \rangle = 0~ \] 由于 \( a_{k\lambda}(0) | \text{vac} \rangle = 0 \)，然而与自由场相关的能量密度是无限的： \[ \frac{1}{4\pi} \langle \mathbf{E}_0^2(t) \rangle = \frac{1}{4\pi} \sum_{\mathbf{k} \lambda} \sum_{\mathbf{k'} \lambda'} \sqrt{\frac{2\pi \hbar \omega_k}{V}} \sqrt{\frac{2\pi \hbar \omega_{k'}}{V}} \times \langle a_{\mathbf{k} \lambda}(0) a_{\mathbf{k'} \lambda'}^{\dagger}(0) \rangle~ \] \[ = \frac{1}{4\pi} \sum_{\mathbf{k} \lambda} \left( \frac{2\pi \hbar \omega_k}{V} \right) = \int_0^{\infty} d\omega \, \rho_0(\omega)~ \] 这点非常重要，因为零点场能量 \( H_F \) 不会影响 \( a_{k\lambda} \) 的海森堡方程，因为它是一个常数（即一个普通的数字，而不是算符），并且与 \( a_{k\lambda} \) 对易。因此，我们可以像通常那样从哈密顿量中去掉零点场能量。但零点场作为场方程的均匀解重新出现。因此，处于真空中的带电粒子将始终看到一个无限密度的零点场。这就是量子电动力学中的一种无穷大的来源，它不能通过简单地去掉场哈密顿量中 \( \sum_{k\lambda} \frac{\hbar \omega_k}{2} \) 这一项来消除。

　　 自由场实际上对于理论的形式一致性是必要的。特别是，它对于保持对易关系是必要的，这是量子理论中时间演化单元性要求的： \[ [z(t), p_z(t)] = [U^\dagger(t) z(0) U(t), U^\dagger(t) p_z(0) U(t)] = U^\dagger(t) [z(0), p_z(0)] U(t) = i\hbar U^\dagger(t) U(t) = i\hbar~ \] 我们可以通过操作符运动方程的形式解来计算 \([z(t), p_z(t)]\)： \[ \mathbf{\ddot{x}} + \omega_0^2 \mathbf{x} - \tau \mathbf{\overset{...}{x}} = \frac{e}{m} \mathbf{E}_0(t)~ \] 利用以下事实： \[ \left[a_{\mathbf{k} \lambda}(0), a_{\mathbf{k'} \lambda'}^\dagger(0)\right] = \delta_{\mathbf{kk'}}^3, \delta_{\lambda \lambda'}~ \] 并且粒子和场算符在相等时间下对易，我们得到： \[ = [z(t), m \dot{z}(t)] + [z(t), \frac{e}{c} A_z(t)] = [z(t), m \dot{z}(t)] = \left( \frac{i \hbar e^2}{2 \pi^2 m c^3} \right) \left( \frac{8\pi}{3} \right) \int_0^\infty \frac{d\omega \, \omega^4}{\left( \omega^2 - \omega_0^2 \right)^2 + \tau^2 \omega^6}~ \] 对于考虑的偶极振荡器，可以假设辐射阻尼率与自然振荡频率相比很小，即 \( \tau \omega_0 \ll 1 \)。那么上面的被积函数在 \( \omega = \omega_0 \) 处 sharply 峰值，并且： \[ [z(t), p_z(t)] \approx \frac{2i \hbar e^2}{3 \pi m c^3} \omega_0^3 \int_{-\infty}^{\infty} \frac{dx}{x^2 + \tau^2 \omega_0^6} = \left( \frac{2i \hbar e^2 \omega_0^3}{3 \pi m c^3} \right) \left( \frac{\pi}{\tau \omega_0^3} \right) = i \hbar~ \] 通过在方程中加入自由场 \( E_0(t) \)，我们可以看到，若没有自由场，操作符 \( x(t) \) 将会呈指数衰减，且当 \( t \gg \frac{1}{\tau \omega_0^2} \) 时，类似 \( [z(t), p_z(t)] \) 的对易关系将趋近于零。然而，加入真空场后，对易关系始终为 \( i \hbar \)，这正是单元性要求的，并且我们刚刚已经证明了这一点。对于自由粒子的情况，也可以得到类似的结果。

　　 这里展示的是一个 “波动-耗散关系” 的例子。一般来说，如果一个系统与一个可以以有效不可逆的方式从系统中提取能量的浴（环境）耦合，那么浴也必须引起波动。波动与耗散是密切相关的，我们无法只拥有其中之一。在当前的例子中，偶极振荡器与电磁场的耦合有一个耗散成分，表现为零点（真空）场；考虑到辐射反应的存在，真空场也必须存在，以保持规范对易关系及其所包含的一切。

　　 真空场的谱密度由辐射反应场的形式决定，反之亦然：由于辐射反应场随 \( x \) 的三阶导数变化，真空场的谱能量密度必须与 \( \omega \) 的三次方成正比，以使得 \( [z(t), p_z(t)] \) 保持不变。与此相对，若耗散力与 \( \dot{x} \) 成正比，则波动力必须与 \( \omega \) 成正比，以保持规范对易关系。这种耗散形式与波动谱密度之间的关系是波动-耗散定理的本质。

　　 对于与真空场耦合的谐振子，保持规范对易关系意味着振荡子的零点能量得以保持。很容易证明，在几次阻尼时间后，振荡子的零点运动实际上是由驱动的零点场维持的。

量子色动力学真空

　　 量子色动力学（QCD）真空是量子色动力学的真空态。它是一个非微扰的真空态，具有非零的凝聚物，例如胶子凝聚物和夸克凝聚物，这些凝聚物在包含夸克的完整理论中起作用。这些凝聚物的存在表征了夸克物质的束缚相。在技术术语上，胶子是媒介夸克之间强相互作用的矢量规范玻色子。胶子本身携带强相互作用的色荷，这与光子不同，后者虽然介导电磁相互作用，但不具有电荷。因此，胶子不仅参与强相互作用，还在其中起到媒介作用，这使得 QCD 比量子电动力学（QED）更加复杂，因为它需要处理非线性方程来描述这些相互作用。

希格斯场

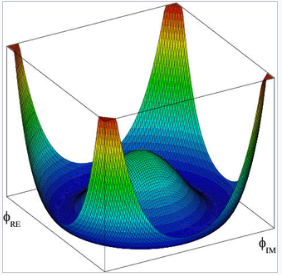
　　 标准模型假设存在一个叫做希格斯场（符号：ϕ）的场，它具有一个非常特殊的性质：在其基态（零点能）经过重正化后，幅度非零；即，它有一个非零的真空期望值。它之所以能产生这种效果，是因为它有一个不寻常的 “墨西哥帽” 形势能，且其最低 “点” 不在其 “中心”。在某个极高的能量水平以下，这种非零的真空期望值自发地破坏了电弱规范对称性，进而引发了希格斯机制，并触发了与该场相互作用的粒子获得质量。希格斯机制在任何带电场具有真空期望值时都会发生。这个效应的产生是因为希格斯场的标量场分量被重质量玻色子 “吸收” 作为自由度，并通过尤卡瓦耦合与费米子相互作用，从而产生预期的质量项。希格斯场在基态的期望值（即真空期望值或 VEV）是⟨ϕ0⟩ = v/√2，其中 v = |μ|/√λ。该参数的测量值大约为 246 GeV/c²。它具有质量的单位，并且是标准模型中唯一的自由参数，不是一个无量纲数。

　　 希格斯机制是一种发生在真空中的超导现象。当整个空间充满带电粒子的海洋时，希格斯场便具有非零的真空期望值。与填充空间的真空能量相互作用，防止某些力在长距离上传播（正如超导介质中发生的情况；例如，在金兹堡–兰道理论中）。

7. 实验观察

　　 零点能具有许多已观察到的物理后果。[11] 需要注意的是，零点能不仅仅是数学形式主义的一个副作用，例如，通过重新定义能量零点或者认为它是一个常数，因此对海森堡运动方程没有影响，从而将其忽略。[100] 实际上，这样的处理可能会在更深层次的、尚未发现的理论中引发问题。[101] 例如，在广义相对论中，能量的零点（即真空的能量密度）对宇宙学常数有所贡献，这种宇宙学常数是爱因斯坦引入的，用于获得他的场方程的静态解。[102] 所有量子场的真空零点能密度极为庞大，即使我们基于合理的物理论证切除最大允许的频率，它仍然巨大。这意味着宇宙学常数比观测所限制的大约高出 120 个数量级。这个 “宇宙学常数问题” 仍然是物理学中最难解的谜题之一。[103]

卡西米尔效应

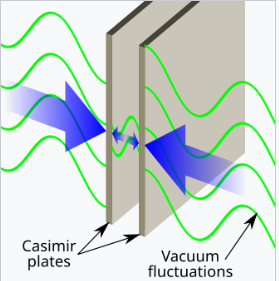
　　 一个通常被作为零点能存在的证据的现象是卡西米尔效应，该效应由荷兰物理学家亨德里克·卡西米尔于 1948 年提出。他考虑了在一对接地的中性金属板之间的量子化电磁场。真空能量包含来自所有波长的贡献，除了那些由于板间距而被排除的波长。随着板之间的距离减小，更多的波长被排除，真空能量减少。能量的减少意味着一定有一个力在板移动时做功。

　　 从 20 世纪 50 年代起，早期的实验测试给出了积极的结果，显示该力是真实的，但其他外部因素不能完全排除为主要原因，实验误差的范围有时接近 100%。[104][105][106][107][108] 这一情况在 1997 年发生了变化，Lamoreaux[109] 最终证明了卡西米尔力是真实的。从那时起，结果已多次被重复验证。[110][111][112][113]

　　 2009 年，Munday 等人[114] 发表了实验证明，卡西米尔力（如 1961 年预测的那样[115]）不仅可以是吸引力，也可以是排斥力。排斥性的卡西米尔力可能允许物体在流体中进行量子悬浮，并可能引领一种新型的可切换纳米尺度设备，具有超低静摩擦。[116]

　　 卡西米尔效应的一个有趣的假设副作用是 Scharnhorst 效应，这是一种假设现象，其中光信号在两个紧密间隔的导体板之间的传播速度稍微快于光速 c。[117]

朗姆位移

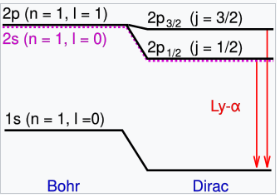
　　 电磁场的量子波动具有重要的物理后果。除了卡西米尔效应外，它们还导致氢原子中两个能级（2S₁/₂ 和 2P₁/₂，使用术语符号表示）之间的能量劈裂，而这一现象并没有被狄拉克方程预测，按照该方程，这两个状态应该具有相同的能量。带电粒子可以与量子化真空场的波动相互作用，从而导致能量的微小变化；这一效应被称为朗姆位移（Lamb shift）。该位移约为 4.38×10⁻⁶ eV，约为 1s 和 2s 能级能量差的 10⁻⁷，频率单位中约为 1,058 MHz。这个位移的一小部分（约 27 MHz ≈ 3%）并非来源于电磁场的波动，而是来源于电子-正电子场的波动。虚拟电子-正电子对的产生有屏蔽库仑场的效应，并充当真空介电常数。在缪子原子中，这一效应要更为显著。

精细结构常数

　　 通过引入 \( \hbar \)（普朗克常数除以 \( 2\pi \)）、\( c \)（光速）和 \( e^2 = \frac{q_e^2}{4\pi\varepsilon_0} \)（电磁耦合常数，表示电磁力的强度，其中 \( q_e \) 是电子电荷的绝对值，\( \varepsilon_0 \) 是真空介电常数），我们可以构造一个无量纲量，称为**精细结构常数**： \[ \alpha = \frac{e^2}{\hbar c} = \frac{q_e^2}{4\pi\varepsilon_0\hbar c} \approx \frac{1}{137}~ \] 精细结构常数是量子电动力学（QED）的耦合常数，决定了电子与光子相互作用的强度。然而，由于电子-正电子场的零点能量波动，精细结构常数实际上并非真正的常数。[121] 零点能量引起的量子波动对电荷有屏蔽效应：由于（虚拟）电子-正电子对的产生，粒子在远处测得的电荷要比在靠近粒子时测得的电荷小得多。

　　 根据海森堡不确定性原理： \[ \Delta_x \Delta_p \geq \frac{1}{2}\hbar~ \] 其中 \( \hbar = \frac{h}{2\pi} \)，\( \Delta_x \) 和 \( \Delta_p \) 分别是位置和动量的不确定性。这意味着较短的距离对应于较大的动量，因此需要高能粒子来探测短距离。量子电动力学的结论是，精细结构常数是能量的递增函数。研究表明，在 \( Z^0 \) 玻色子静止能量（\( m_Zc^2 \approx 90 \, \text{GeV} \)）的能量尺度下，精细结构常数变为： \[ \alpha \approx \frac{1}{129}~ \] 而在低能量情况下，\( \alpha \approx \frac{1}{137} \)。[122][123] 消除零点能无穷大的重正化过程允许选择任意的能量（或距离）尺度来定义 \( \alpha \)。总的来说，\( \alpha \) 依赖于所研究过程的特征能量尺度，也依赖于重正化过程的具体细节。在高能物理的精密实验中，精细结构常数的能量依赖性已被观察到多年。

真空双折射

　　 在强静电场的存在下，理论预测虚粒子会从真空态中分离并形成真实的物质。[需要引用] 电磁辐射可以转化为物质，反之亦然，这一事实在量子电动力学中引入了全新的特性。其中最重要的一个后果是，即使在真空中，麦克斯韦方程也必须被更复杂的公式所取代。通常情况下，无法将真空中的过程与涉及物质的过程分离，因为如果电磁场的波动足够强，电磁场可以创造物质。这导致了极为复杂的非线性相互作用——引力会对光产生影响，同时光也会对引力产生影响。

　　 这些效应最早由维尔纳·海森堡和汉斯·海因里希·欧拉于 1936 年预测，[124] 同年维克多·魏斯科普夫也独立提出了类似的观点，他指出：“真空的物理性质来源于物质的‘零点能量’，这也依赖于外场强度作用下的缺失粒子，因此为纯麦克斯韦场能量贡献了一个附加项。”[125][126] 因此，强磁场会改变真空中所包含的能量。

　　 电磁场被认为会变得非线性的临界尺度被称为Schwinger 极限。在这一点上，真空表现出双折射介质的所有特性，因此，原则上可以在空旷空间中观察到偏振框架的旋转（即法拉第效应）。[127][128]

　　 爱因斯坦的狭义和广义相对论都认为光应该可以自由穿过真空而不受改变，这一原则被称为洛伦兹不变性。然而，理论上，由于量子波动引起的光的非线性自相互作用在足够强的情况下，可能会导致这一原则被可测量地违反。几乎所有的量子引力理论都预测，洛伦兹不变性并非自然界的精确对称性。据预测，光在真空中的传播速度取决于其方向、偏振以及局部磁场的强度。[129]

　　 目前已经有一些不确定的结果声称通过发现来自遥远星系的光偏振平面的旋转，展示了洛伦兹不变性被违反的证据。[130] 真空双折射的第一个具体证据于 2017 年发布，当时一组天文学家观测了来自 RX J1856.5-3754 恒星的光，这是一颗已知距离地球最近的中子星。[131][132]

　　 米兰国家天体物理研究所的 Roberto Mignani 领导了这支天文学团队，他评论道：“当爱因斯坦 100 年前提出广义相对论时，他完全没有想到它会被用于导航系统。这一发现的影响可能也需要在更长的时间尺度上被实现。”[133] 研究团队发现来自该恒星的可见光发生了大约 16%的线性偏振。如果双折射是由光穿过星际气体或等离子体引起的，这种效应不应超过 1%。然而，要获得确凿的证据，还需要在其他波长上以及对其他中子星重复观测。在 X 射线波长下，量子波动引起的偏振应该接近 100%。[134]

　　 尽管目前尚无可进行这种测量的望远镜，但已经提出了几种可能很快能够验证这一结果的 X 射线望远镜，例如中国的硬 X 射线调制望远镜（HXMT）和美国宇航局的成像 X 射线偏振探测器（IXPE）。

8. 推测与其他现象的关联

暗能量

　　 20 世纪 90 年代末，科学家发现非常遥远的超新星比预期的更暗，这表明宇宙的膨胀不是在减速，而是在加速。[136][137] 这一发现重新引发了对爱因斯坦宇宙学常数的讨论。物理学家长期认为宇宙学常数等于零，但这一发现表明它实际上可能是一个小的正值。这表明空旷的空间可能施加了一种形式的负压力或能量。

　　 目前尚无自然候选者可以解释所谓的暗能量的来源，但当前最好的猜测是它可能是真空的零点能量。然而，这一猜测与观测值相差了 120 个数量级。[138]

　　 欧洲航天局的欧几里得望远镜于 2023 年 7 月 1 日发射升空，它将绘制距离地球多达 100 亿光年的星系分布图。[139] 通过观察暗能量如何影响这些星系的排列和形状，该任务将帮助科学家探讨暗能量的强度是否随时间变化。如果发现暗能量在时间上有所变化，这将表明它可能是由 “第五元素”（quintessence）引起的，而不是宇宙学常数。在这种情况下，观察到的加速是由一个标量场的能量导致的。然而，目前尚无第五元素的确凿证据，但这一可能性尚未被排除。与宇宙学常数相比，第五元素通常预测宇宙膨胀的加速度略低。

　　 一些科学家认为，第五元素最好的证据可能来自对爱因斯坦等效原理的违反以及空间或时间中基本常数的变化。[140] 标量场被粒子物理标准模型和弦理论所预测，但类似于宇宙学常数问题（或构建宇宙暴胀模型的问题），同样的问题会出现：重正化理论预测标量场会因为零点能量再次获得较大的质量。

宇宙暴胀

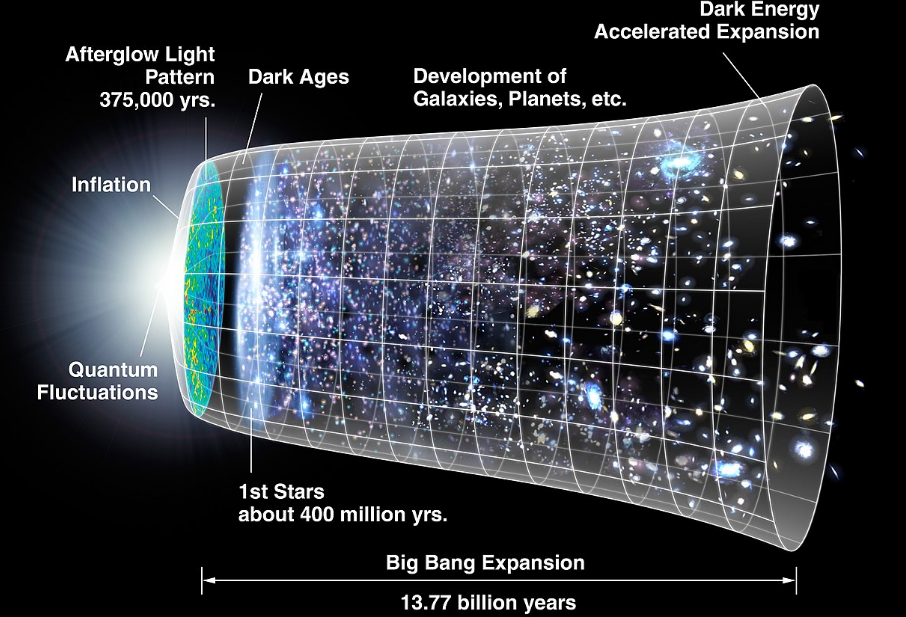
　　 宇宙暴胀是指在大爆炸之后的一个加速膨胀阶段。它解释了宇宙大尺度结构的起源。科学家认为，在微观暴胀时期，由零点能引起的量子真空波动后来被放大到宇宙尺度，成为星系和宇宙结构的引力种子（参见星系的形成与演化和结构形成）。[141] 许多物理学家还认为，暴胀解释了为什么宇宙在所有方向上看起来是相同的（各向同性）、为什么宇宙微波背景辐射分布均匀、为什么宇宙是平坦的，以及为什么没有观察到磁单极。

　　 暴胀的机制尚不明确，它在效应上类似于暗能量，但却是一个能量更高且持续时间更短的过程。与暗能量一样，最好的解释是某种形式的由量子波动引起的真空能量。此外，暴胀可能导致了重子生成，即在宇宙早期产生重子和反重子不对称性的假设物理过程，但这一点还远未确定。

宇宙学

　　 保罗·S·韦森（Paul S. Wesson）研究了假设零点能量真实存在的宇宙学影响。[142] 在众多困难中，广义相对论要求这种能量不能引力化，因此它不能类似于电磁辐射。

9. 替代理论

　　 关于量子化真空场的零点波动是否 “真实” 存在，即它们是否具有无法通过同样有效的替代理论解释的物理效应，这一问题长期以来存在争论。[143] 尤其是施温格（Schwinger）试图通过他的 “源理论”（Source Theory）在不涉及零点波动的情况下构建量子电动力学（QED）。[144] 通过这种方法，可以在不参考波动场的情况下推导出卡西米尔效应。这种推导首次由施温格（1975 年）针对标量场给出，[145] 后来施温格、DeRaad 和 Milton（1978 年）将其推广到电磁场的情况。[146] 他们指出，“真空实际上被认为是一个所有物理属性均为零的状态。”

　　 Jaffe（2005 年）[147] 也强调了一种类似的方法来推导卡西米尔效应，他指出：“零点波动的概念是一种启发式和计算辅助工具，用于描述卡西米尔效应，但在 QED 中并非必需。”

　　 然而，Milonni 证明了真空场对于 QED 形式一致性的重要性。[148] 现代物理学尚未找到比包含零点能更好的方法来构建规范不变、可重正化的理论，零点能似乎是任何统一理论尝试所必需的。[149] 然而，正如 Jaffe 所指出的，“没有任何已知的现象，包括卡西米尔效应，能够证明零点能量是‘真实’的。”[147]

10. 混沌与涌现现象

　　 经典电磁学、量子电动力学（QED）和标准模型中使用的数学模型都将电磁真空视为一个线性系统，没有整体可观测的结果。例如，对于卡西米尔效应、朗姆位移等现象，这些现象可以通过其他机制解释，而不是通过真空的作用，例如对场算符的正规排序进行任意更改即可（参见替代理论部分）。这是因为电磁学被视为一个 \( U(1) \) 规范理论，从拓扑学的角度来看，这种理论不允许场与自身之间的复杂相互作用。[150]

　　 在更高对称群以及现实中，真空并不是一种平静、随机波动、大体无形且被动的物质，而有时可以被视为一种湍流的虚拟等离子体，它可能具有复杂的涡旋（即孤子与粒子相对）、纠缠态以及丰富的非线性结构。[151]

　　 有许多已观察到的非线性物理电磁现象，例如阿哈罗诺夫-玻姆效应（AB 效应）[152][153]、Altshuler–Aronov–Spivak 效应（AAS 效应）[154]、Berry 相位[155]、阿哈罗诺夫–安南丹相位[156]、潘查拉坦姆相位[157]、Chiao–Wu 相位旋转效应[158]、约瑟夫森效应[159][160]、量子霍尔效应[161]、德哈斯–范阿尔芬效应[162]、萨尼亚克效应以及许多其他可观测的现象。这些现象表明，电磁势场具有真实的物理意义，而不仅仅是数学上的构造。[163]

　　 因此，一个包罗万象的理论不会像目前一样将电磁学限制为局域力，而是需要将其描述为 \( SU(2) \) 规范理论或更高几何形式。更高的对称性允许非线性、非周期行为的出现，这些行为表现为各种复杂的非平衡现象，而这些现象不会出现在线性化的 \( U(1) \) 理论中，例如多稳态、对称性破缺、混沌和涌现。[164]

　　 今天被称为麦克斯韦方程的方程实际上是原始方程的简化版本，由赫维赛德（Heaviside）、菲茨杰拉德（FitzGerald）、洛奇（Lodge）和赫兹（Hertz）重新表述。原始方程使用了哈密顿更具表现力的四元数符号，[165] 一种克利福德代数（Clifford algebra），它完全包含了今天广泛使用的标准麦克斯韦矢量方程。[166] 在 19 世纪 80 年代末，关于矢量分析与四元数相对优劣的争论甚嚣尘上。根据赫维赛德的说法，电磁势场纯粹是形而上的，一个任意的数学虚构，需要被 “消灭”。[167] 最终的结论是，如果理论本质上是局域性的，那么就不需要四元数提供的更深层次的物理见解。局域矢量分析自此成为使用麦克斯韦方程的主导方法。然而，这种严格的矢量方法在电磁学的一些领域导致了限制性的拓扑理解。例如，特斯拉振荡-穿梭电路中的能量传输动力学只能通过四元数代数或更高阶 \( SU(2) \) 对称性来全面理解。[168]

　　 虽然有人认为四元数与狭义相对论不兼容，[169] 但多篇论文展示了将其纳入相对论的方法。[170][171][172][173]

　　 高能量密度等离子体是非线性电磁学的一个很好例子。在这种情况下，会出现涡旋现象，这种现象似乎通过增加电磁场内的能量梯度违反了热力学第二定律，并通过产生捕获和集中自身及周围磁场的离子电流违反了麦克斯韦定律。特别是，麦克斯韦方程中由洛伦兹力定律描述的部分在这些无力涡旋中被违反。[174][175][176]

　　 这些表面上的违反是因为经典和量子电动力学（QED）中的传统守恒定律仅表现为线性 \( U(1) \) 对称性（特别是根据扩展的诺特定理，[177] 守恒定律，例如热力学定律，不一定适用于耗散系统，[178][179] 而这些系统通常用更高对称性的规范来表示）。热力学第二定律规定，在封闭的线性系统中，熵流只能是正的（或者在一个循环结束时精确为零）。然而，在远离平衡的开放非线性热力学系统中，只要这种涌现的秩序加速了整个系统的熵流，负熵（即更高的秩序、结构或自组织）可以自发出现。

　　 1977 年诺贝尔化学奖授予热力学家伊利亚·普里戈金（Ilya Prigogine），[180] 以表彰他描述这一概念的耗散系统理论。普里戈金将这一原则描述为 “通过波动产生的秩序”[181] 或 “从混沌中产生秩序”。[182]

　　 有些人认为，宇宙中所有的涌现秩序，从星系、太阳系、行星、天气、复杂化学、进化生物学，到甚至意识、技术和文明，都是热力学耗散系统的例子；自然通过选择这些结构来加速宇宙中的熵流到越来越高的程度。[183] 例如，据估计，人类身体单位质量的能量耗散效率比太阳高 10,000 倍。[184]

　　 考虑到非线性系统中复杂而适应性的行为，近年来对绝对零温度下发生的新型相变进行了大量研究。这些是由电磁场波动引发的量子相变，而这些波动是零点能量的结果。[185] 零点波动引起的自发相变的一个很好的例子可以在超导体中找到。超导性是最广为人知且经实验证明的宏观电磁现象之一，其基础被认为源于量子力学。超导状态下电场和磁场的行为由伦敦方程（London equations）支配。然而，在一系列期刊文章中，有人质疑是否可以对量子力学规范化的伦敦方程进行纯经典的推导。[186]

　　 例如，Bostick[187][188] 声称，他证明了伦敦方程确实具有经典起源，适用于超导体以及某些无碰撞等离子体。他特别指出，等离子体聚焦中的贝尔特拉米涡旋（Beltrami vortices）表现出与第二类超导体相同的配对磁通管形态。[189][190] 其他研究者也注意到了这种联系。Fröhlich[191] 证明，可压缩流体的流体动力学方程结合伦敦方程，可以得到一个宏观参数 \( \mu \)（即电荷密度与质量密度的比值），而无需涉及量子相位因子或普朗克常数。

　　 本质上，有人提出，贝尔特拉米等离子体涡旋结构至少能够模拟第一类和第二类超导体的形态。这是因为离子和电子组成的涡旋结构的 “有序” 耗散能量远远超过了 “无序” 耗散的随机热能量。从无序波动到有序螺旋结构的转变是一个相变，涉及凝聚态能量的变化（即基态或零点能量），但不伴随任何温度的升高。[192]

　　 这表明零点能量可以具有多个稳定态（参见量子相变、量子临界点、拓扑简并性、拓扑序[193]），而且整个系统的结构可以独立于还原论或确定论的观点，表明 “经典” 宏观秩序也可以因果地影响量子现象。此外，贝尔特拉米涡旋的成对产生已被拿来与真空中虚粒子对的成对产生的形态进行比较。

　　 真空能量可以具有多个稳定能量态的观点是导致宇宙暴胀的主要假设之一。事实上，有人认为，这些早期的真空波动导致了宇宙的膨胀，从而保证了从混沌中产生秩序所需的非平衡条件。因为如果没有这样的膨胀，宇宙将达到热力学平衡状态，任何复杂性都无法存在。

　　 随着宇宙的持续加速膨胀，宇宙创造了一个能量梯度，这个梯度增加了 “自由能”（即可用的、可利用的或用于有用功的潜在能量），使宇宙能够创造出越来越复杂的秩序形式。[194][195]

　　 地球环境之所以没有衰退到平衡状态，唯一的原因是它每天从阳光中获得能量，而这又归因于太阳通过熵 “污染” 了星际空间。太阳的核聚变能量仅仅是由于物质因宇宙膨胀产生的引力非平衡才得以实现。因此，从本质上讲，真空能量可以被视为整个宇宙结构的根本原因。

　　 关于人类是否能够改变真空能量的形态以创造用于有用功的能量梯度，这一问题备受争议。

11. 声称的应用

　　 物理学家普遍否定利用零点能量场来获取有用能量（功）或无补偿动量的可能性；这样的努力被视为等同于制造永动机。[需要引用]

　　 尽管如此，“自由能” 的吸引力推动了相关研究，这通常被归类为边缘科学。早在 1889 年（量子理论或零点能量被发现之前），尼古拉·特斯拉就提出，可以从自由空间中获取有用能量，当时假定这是一种无处不在的 “以太”。[196] 此后，也有人声称通过零点能量或真空能量获取能量，但大量的伪科学文献使这一主题受到了嘲笑。[197][198] 尽管科学界普遍拒绝，但利用零点能量仍是研究的一个兴趣点，尤其在美国，它吸引了主要航空航天/国防承包商和美国国防部的关注，也在中国、德国、俄罗斯和巴西得到了关注。[197][199]

卡西米尔电池与发动机

　　 通常的假设是卡西米尔力几乎没有实际用途；有人认为，唯一可以从两块板中实际获得能量的方法是让它们靠拢（再将它们分开会需要更多能量），因此它是自然界中的一次性微小力。[197] 1984 年，罗伯特·福沃德（Robert Forward）发表了一项研究，展示了如何构建 “真空波动电池”；这种电池可以通过让电力作用稍强于卡西米尔力来重新扩展板，从而实现充电。[200]

　　 1999 年，曾任职于美国国家航空航天局喷气推进实验室（NASA JPL）的 Pinto 在《物理评论》上发表了一项关于 “卡西米尔发动机” 的思想实验（Gedankenexperiment）。该论文表明，从卡西米尔效应中实现持续正能量交换是可能的，甚至在摘要中声称：“如果没有其他替代解释，人们应该得出结论，在无副产品的永续自由能量生产领域可以实现重大技术突破。”[201]

　　 科罗拉多大学的 Garret Moddel 指出，他认为此类装置依赖于卡西米尔力是一种非保守力的假设，但他主张有充分证据（例如 Scandurra (2001) 的分析[202]）表明卡西米尔效应是保守力，因此尽管这种发动机可以利用卡西米尔力完成有用功，但其输出能量不会超过输入系统的能量。[203]

　　 2008 年，DARPA 征集了关于 “卡西米尔效应增强”（CEE）的研究提案。该计划的目标是开发基于卡西米尔力工程的新方法，以控制和操纵表面间的吸引力和排斥力。[204]

　　 2008 年，Haisch 和 Moddel 获得了一项专利[205]，其描述了一种能够利用穿过卡西米尔腔体的气体从零点波动中提取能量的装置。Moddel 于 2012 年对该概念进行了一次实验测试[206]，结果似乎显示出无法归因于其他来源的过量能量。然而，尚未确凿证明这些能量来源于零点能量，并且这一理论需要进一步研究。[207]

单一热浴

　　 1951 年，Callen 和 Welton 证明了量子波动-耗散定理（Fluctuation-Dissipation Theorem, FDT），该定理最初以经典形式由 Nyquist 于 1928 年提出，[76][77] 用于解释在电路中观察到的约翰逊噪声。[78] 波动-耗散定理表明，当某个系统以有效不可逆的方式耗散能量时，连接的热浴也必须发生波动。波动与耗散是密切相关的，不可能只有其中之一。FDT 的一个重要推论是，真空可以被视为一个与耗散力耦合的热浴，因此部分能量可以从真空中提取用于潜在的有用工作。[79]

　　 这样的理论遭到了抵制：Macdonald（1962）[208] 和 Harris（1971）[209] 声称，从零点能量中提取能量是不可能的，因此 FDT 不可能成立。Grau 和 Kleen（1982）[210] 以及 Kleen（1986）[211] 认为，连接到天线的电阻的约翰逊噪声必须满足普朗克热辐射公式，因此噪声在零温度时必须为零，而 FDT 因此无效。Kiss（1988）[212] 指出，零点项的存在可能表明存在重正化问题，即一种数学上的伪影，产生了一个在测量中实际上不存在的不物理项（类似于量子电动力学中基态的重正化问题）。后来，Abbott 等人（1996）得出了不同但不明确的结论，即 “零点能量是无限的，因此应该被重正化，但不是‘零点波动’”。[213]

　　 尽管存在这些批评，实验已经证明在某些量子非经典条件下，FDT 是成立的。零点波动确实会对耗散能量的系统产生贡献。[80] 2000 年，Armen Allahverdyan 和 Theo Nieuwenhuizen 发表了一篇论文，展示了通过利用某些量子力学特性，从单一热浴中提取零点能量用于有用工作的可行性，并且不违反热力学定律。[81]

　　 越来越多的论文显示，在某些情况下，通过利用量子波动的负熵，可以违反经典热力学定律，例如对卡诺效率的限制。[82][214][215][216][217][218][219][220][221][222]

　　 尽管多年来努力协调量子力学与热力学，它们的兼容性仍然是一个未解决的基础性问题。量子特性可以在多大程度上改变经典热力学界限，仍然未知。[223]

太空旅行与引力屏蔽

　　 利用零点能进行太空旅行仍然是一个推测性的领域，并未成为主流科学共识的一部分。完整的量子引力理论（能够处理零点能等量子现象在引力中的作用）尚未建立。一些推测性论文提出了零点能量与引力屏蔽效应之间的关系，[16][224][225][226] 但这种相互作用（如果存在的话）尚未被完全理解。

　　 根据广义相对论，旋转的物质可以产生一种新的自然力，被称为引力磁相互作用（gravitomagnetic interaction），其强度与旋转速率成正比。[227] 在某些条件下，引力磁场可能表现为排斥性。例如，在中子星中，这种效应可能会产生与迈斯纳效应类似的引力现象，但理论认为，这种力的强度极为微弱。[228]

　　 1963 年，Hughes 研究实验室的物理学家兼航空工程师罗伯特·福沃德（Robert Forward）发表了一篇论文，阐述了在广义相对论框架内实现 “反引力” 效应的可能性。[229] 由于所有原子都有自旋，引力导磁率可能因材料而异。具有非线性特性的材料可以增强时变引力场，从而产生一种与重力相对抗的强环形引力场。这种效应类似于铁的非线性电磁导磁率，使其成为变压器的有效核心（如铁制成的环形结构），其特性依赖于磁导率。[230][231][232]

　　 1966 年，Dewitt 首次发现了超导体中引力效应的重要性。他证明了磁性引力场的存在必然伴随着磁通量量子化现象。[233] 1983 年，Ross 对 Dewitt 的工作进行了大幅扩展。[234]

　　 1971 年至 1974 年，通用电气航空航天部门的科学家亨利·威廉·华莱士（Henry William Wallace）获得了三项专利。[235][236][237] 华莱士利用 Dewitt 的理论开发了一种实验装置，用于生成和检测次级引力场，他将其命名为 “运动质量场”（kinemassic field，现更广为人知为引力磁场）。在他的三项专利中，华莱士描述了检测引力磁场的三种不同方法：通过测量支点上物体运动的变化、检测半导体晶体中的横向电压，以及测量具有自旋排列核的晶体材料比热的变化。目前没有公开的独立测试验证华莱士的设备。如果这种效应存在，其影响可能非常微小。[238][239][240][241][242][243]

　　 1980 年，《新科学家》的一篇文章提到华莱士的专利时表示：“尽管华莱士的专利最初被认为是异想天开的，但观察者认为，他的发明现在受到美国军事当局的认真且秘密的研究。军方可能后悔这些专利已被授予，因此任何人都可以阅读。”[244]

　　 在为爱德华兹空军基地宇航实验室准备的一项电推进研究中再次提到华莱士的专利，该研究指出：“这些专利写得非常可信，包括部件编号、一些部件的来源以及数据图表。尝试通过专利地址和其他渠道联系华莱士未果，他的工作也无迹可寻。从广义相对论的角度来看，这一概念是可以在某种程度上被合理化的，因为预期旋转的时变场会发射引力波。”[245]

　　 1986 年，美国空军的火箭推进实验室（RPL）在爱德华兹空军基地的小企业研究与创新计划下，征集 “非传统推进概念” 提案。六个研究领域之一是 “用于推进的深奥能量来源，包括真空空间的量子动力能量……”[199][246] 同年，BAE 系统公司启动了 “绿色辉光项目”（Project Greenglow），旨在为新型推进系统及其动力来源的研究提供焦点。[199][246]

　　 1988 年，Kip Thorne 等人发表了一项研究，展示了在时空中可以存在可穿越的虫洞，前提是它们被某种形式的负能量奇异物质生成的量子场贯穿。[247] 1993 年，Scharnhorst 和 Barton 证明，如果光子在两块卡西米尔板之间传播，其速度会增加，这是一种负能量的例子。[117] 从广义上来说，创建虫洞所需的奇异物质将具有膨胀能量、暗能量或真空零点辐射的排斥性质。[248]

　　 在 Thorne 的工作的基础上，1994 年，Miguel Alcubierre 提出了一种改变空间几何的方法，通过创造一种波，使得航天器前方的空间收缩，后方的空间扩张（参见 Alcubierre 驱动）。[249] 这样，飞船将在被称为 “翘曲气泡”（warp bubble）的平坦空间区域中 “乘波前进”，它自身不会在这个气泡中移动，而是随着驱动器引起的区域移动而被携带。

　　 1992 年，Evgeny Podkletnov 发表了一篇备受争议的论文，[250][251][252][253][254] 声称一种特定类型的旋转超导体可以屏蔽引力。与此同时，1991 年至 1993 年，Ning Li 和 Douglas Torr 独立发表了多篇关于超导体中引力效应的文章。[255][256][257] 他们发现，在第二类超导体材料中，引力磁通量的来源是晶格离子的自旋排列。他们在第三篇论文中指出：“晶格离子自旋的相干排列将生成可检测的引力磁场，并且在一个时变的外加磁矢势场的作用下，将生成可检测的引力电场。”

　　 关于所产生的力的大小，有人提出质疑，[258][259] 但也有人支持这一结果。[260][261] 1997 年，Li 发表了一篇论文，尝试复制 Podkletnov 的结果，发现这种效应非常小，甚至可能不存在。[262] 据报道，Li 于 1999 年离开阿拉巴马大学，创立了 AC Gravity LLC 公司。[263] 2001 年，AC Gravity 公司获得了美国国防部 448,970 美元的资助，用于继续反重力研究。资助期在 2002 年结束，但这项研究的任何结果均未公开。[264]

　　 2002 年，波音公司位于西雅图的先进研究与开发机构 Phantom Works 直接联系了 Evgeny Podkletnov。但由于俄罗斯的技术转让管控，Phantom Works 的尝试被阻止。当时，波音 Phantom Works 的即将离任负责人 George Muellner 中将证实，波音与 Podkletnov 合作的尝试被俄罗斯政府阻止。他评论道：“这一物理原理——而且 Podkletnov 的装置并不是唯一的——似乎是有效的……这里有基本的科学理论，它们并未违反物理定律。问题在于，这些科学理论是否可以被工程化为可行的技术。”[265]

　　 Froning 和 Roach 在 2002 年发表了一篇论文，基于 Puthoff、Haisch 和 Alcubierre 的研究成果。[266] 他们使用流体动力学模拟来建模飞行器（例如 Alcubierre 提议的飞船）与零点场的相互作用。他们将真空场扰动模拟为流体场的扰动，并将施加在飞行器内部的粘性阻力的空气动力学阻力与零点场施加的洛伦兹力进行比较（卡西米尔效应类似的力通过不平衡的零点辐射压力作用在飞行器外部）。研究发现，为实现 Alcubierre 驱动所需的最佳负能量，飞行器应设计为具有环形电磁场的碟状形状。电磁场会显著扭曲飞行器周围的真空场扰动，从而影响空间的渗透率和介电常数。

　　 2009 年，Giorgio Fontana 和 Bernd Binder 提出了一种新方法，可以通过引力波形式提取电磁场和核力的零点能量。[267] 在双诺贝尔奖得主 Linus Pauling 提出的核子球体模型（spheron model）中，[268] 二中子是该结构的组成部分之一。类似于一个处于合适旋转状态的哑铃，但具有核质量密度，二中子几乎是 X 射线和伽马射线频率下理想的引力波源。通过核力介导，电中性二中子与带电核心原子核之间的动力学相互作用，是将核振动转化为二中子的旋转状态并发射引力波的基本机制。

　　 尽管引力和引力波在广义相对论中得到了很好的描述，而广义相对论并不是一个量子理论，这意味着在这一理论中不存在引力的零点能，因此二中子会像任何其他已知的引力波源一样发射引力波。Fontana 和 Binder 的论文指出，具有动态不稳定性的核物种（与电磁场和核力的零点能量相关）并且包含二中子的核物质将会发射引力波。在实验物理中，这种方法尚未被探索。

　　 2014 年，NASA 的 Eagleworks 实验室宣布成功验证了一种利用卡西米尔效应推进的量子真空等离子推进器。[269][270][271] 2016 年，NASA 科学家团队的相关论文首次通过了同行评审。[272] 论文提出，零点场充当导波，推力可能是由于粒子与量子真空相互作用产生的。尽管同行评审并不能保证发现或观察的有效性，但它表明独立科学家审查了实验设置、结果和解释，并未发现方法上的明显错误，并认为结果是合理的。

　　 在论文中，作者识别并讨论了九种潜在的实验误差来源，包括空气流动、电磁辐射泄漏和磁性相互作用。其中一些尚未完全排除，因此需要进一步的同行评审实验来消除这些潜在的误差。[273]

12. 科幻作品中的零点能量

　　 将零点能量作为能源的概念已成为科幻及相关媒体中的一个元素。

13. 另见

• 卡西米尔效应
• 基态
• 朗姆位移
• QED 真空
• QCD 真空
• 量子波动
• 量子泡沫
• 标量场
• 时间晶体
• 拓扑序
• 乌恩鲁效应
• 真空能量
• 真空期望值
• 真空态
• 虚粒子

14. 参考文献

注释

1. Sciama (1991), 第 137 页。
2. Milonni (1994), 第 35 页。
3. Davies (2011)。
4. 参见 Weinberg (1989) 和 Peebles & Ratra (2003) 的综述文章，以及 Shiga (2005)、Siegel (2016) 的媒体评论。
5. Weinberg (2015), 第 376 页。
6. Sciama (1991), 第 138 页。
7. Davies (1985), 第 104 页。
8. Einstein (1995), 第 270–285 页。
9. Battersby (2008)。
10. Itzykson & Zuber (1980), 第 111 页。
11. Milonni (1994), 第 111 页。
12. Greiner, Müller & Rafelski (2012), 第 12 页。
13. Bordag 等 (2009), 第 4 页。
14. Cho (2015)。
15. Choi (2013)。
16. 参见 Haisch, Rueda & Puthoff (1994) 的提议，以及 Matthews (1994, 1995)、Powell (1994) 和 Davies (1994) 的评论。
17. 参见 Urban 等 (2013), Leuchs & Sánchez-Soto (2013) 和 O'Carroll (2013) 的评论。
18. Rugh & Zinkernagel (2002)。
19. "暗能量可能是真空"（新闻稿）。尼尔斯·玻尔研究所，2007 年 1 月 19 日。2017 年 5 月 31 日存档。
20. Wall (2014)。
21. 桑德斯和布朗（1991），第 1 页
22. 康隆（2011），第 225 页
23. 克拉格和欧弗杜因（2014），第 7 页
24. 普朗克（1900）
25. 劳登（2000），第 9 页
26. 克拉格（2012），第 7 页
27. 普朗克（1912a）
28. 米洛尼（1994），第 10 页
29. 参见普朗克（1911、1912a、1912b、1913）和普朗克（1958）的重印本
30. 库恩（1978），第 235 页
31. 爱因斯坦，阿尔伯特；斯特恩，奥托（1913） "Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt" [关于绝对零点下分子激动假设的一些论据]。 《物理年鉴》（德文） 第 345 卷（第 3 期），551–560 页。 Bibcode: 1913AnP...345..551E. doi: [10.1002/andp.19133450309](https://doi.org/10.1002/andp.19133450309)。
32. 爱因斯坦（1993），第 563–565 页
33. 德拜，彼得（1913） "Interferenz von Röntgenstrahlen und Wärmebewegung" [X 射线与热运动的干涉]。 《物理年鉴》（德文） 第 348 卷（第 1 期），49–92 页。 Bibcode: 1913AnP...348...49D. doi: [10.1002/andp.19133480105](https://doi.org/10.1002/andp.19133480105)。
34. 能斯特，瓦尔特（1916） "Über einen Versuch, von quantentheoretischen Betrachtungen zur Annahme stetiger Energieänderungen zurückzukehren" [试图从量子理论考量回归到假设能量连续变化的尝试]。 《德国物理学会报告》（德文） 第 18 卷，83–116 页。
35. 爱因斯坦，阿尔伯特（1920） Äther und Relativitäts-Theorie [以太与相对论]（德文）。柏林：Springer 出版社。
36. 爱因斯坦，阿尔伯特（1922） Jeffery, G. B.; Perrett, W.（编）。 Sidelights on Relativity: Ether and the Theory of Relativity 纽约：Methuen & Co. 第 1–24 页。
37. 本内维茨，库尔特；西蒙，弗朗茨（1923） "Zur Frage der Nullpunktsenergie" [关于零点能问题]。 《物理学杂志》（德文） 第 16 卷（第 1 期），183–199 页。 Bibcode: 1923ZPhy...16..183B. doi: [10.1007/BF01327389](https://doi.org/10.1007/BF01327389)。 S2CID: 121049183。
38. Simon, F. (1934). "Behaviour of Condensed Helium near Absolute Zero" [接近绝对零度时凝聚氦的行为]。 《自然》第 133 卷（3362 期），529 页。 Bibcode: 1934Natur.133Q.529S. doi: [10.1038/133529a0](https://doi.org/10.1038/133529a0)。 S2CID: 4130047。
39. Dugdale, J. S.; Simon, F. E. (1953). "Thermodynamic Properties and Melting of Solid Helium" [固态氦的热力学性质与熔化]。 《皇家学会学报》 第 218 卷（1134 期），291 页。 Bibcode: 1953RSPSA.218..291D. doi: [10.1098/rspa.1953.0105](https://doi.org/10.1098/rspa.1953.0105)。 S2CID: 98061516。
40. Mulliken, Robert S. (1924). "The band spectrum of boron monoxide" [一氧化硼的带状光谱]。 《自然》 第 114 卷（2862 期），349–350 页。 Bibcode: 1924Natur.114..349M. doi: [10.1038/114349a0](https://doi.org/10.1038/114349a0)。 S2CID: 4121118。
41. Heisenberg, W. (1925). "Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen" [关于量子理论中运动学与力学关系的重新解释]。 收录于 Blum, Walter; Rechenberg, Helmut; Dürr, Hans-Peter（编）。 Wissenschaftliche Originalarbeiten [科学原始论文]（德文）。 柏林，海德堡：Springer（1985 年出版）。第 382–396 页。 doi: [10.1007/978-3-642-61659-4_26](https://doi.org/10.1007/978-3-642-61659-4_26)。 ISBN: 978-3-642-64900-4。 OCLC: 7331244990。
42. Kragh (2002), 第 162 页
43. Bohr, Niels (1913). "On the Constitution of Atoms and Molecules, Part I" [关于原子和分子结构，第一部分] (PDF)。 《哲学杂志》第 26 卷（151 期），1–24 页。 Bibcode: 1913PMag...26....1B. doi: [10.1080/14786441308634955](https://doi.org/10.1080/14786441308634955)。
44. Bohr, Niels (1913). "On the Constitution of Atoms and Molecules, Part II Systems Containing Only a Single Nucleus" [关于原子和分子结构，第二部分：仅包含单一核的系统] (PDF)。 《哲学杂志》 第 26 卷（153 期），476–502 页。 Bibcode: 1913PMag...26..476B. doi: [10.1080/14786441308634993](https://doi.org/10.1080/14786441308634993)。
45. Bohr, Niels (1913). "On the Constitution of Atoms and Molecules, Part III Systems containing several nuclei" [关于原子和分子结构，第三部分：包含多个核的系统]。 《哲学杂志》 第 26 卷（155 期），857–875 页。 Bibcode: 1913PMag...26..857B. doi: [10.1080/14786441308635031](https://doi.org/10.1080/14786441308635031)。
46. Jeans, James Hopwood (1915). The mathematical theory of electricity and magnetism[电磁学的数学理论]（第 3 版）。 剑桥：剑桥大学出版社。第 168 页。
47. 薛定谔，埃尔温（1926）。 "Quantisierung als Eigenwertproblem" [作为特征值问题的量子化]。 《物理年鉴》（德文） 第 79 卷（第 13 期），361–376 页。 Bibcode: 1926AnP...385..437S. doi: [10.1002/andp.19263851302](https://doi.org/10.1002/andp.19263851302)。
48. Lieb, E. H.; Seiringer, R.（2009）。 The Stability of Matter in Quantum Mechanics [量子力学中物质的稳定性]。剑桥：剑桥大学出版社。第 2–3 页。 ISBN: 978-0-521-19118-0。 OCLC: 638472161。
49. 玻恩，马克斯；海森堡，维尔纳；乔丹，帕斯库尔（1926）。 "Zur Quantenmechanik. II" [关于量子力学的研究 II]。 《物理学杂志》（德文） 第 35 卷（第 8 期），557–615 页。 Bibcode: 1926ZPhy...35..557B. doi: [10.1007/BF01379806](https://doi.org/10.1007/BF01379806)。 S2CID: 186237037。
50. 爱因斯坦，阿尔伯特（1909）。 "Zum gegenwärtigen Stand des Strahlungsproblems" [关于辐射问题的当前状态]。 《物理学杂志》 第 10 卷，185–193 页。 Bibcode: 1909PhyZ...10..185E。
51. Mehra, J.; Rechenberg, H.（2002）。 The Historical Development of Quantum Theory [量子理论的历史发展]。第 6 卷。Springer 出版社。第 57 页。 ISBN: 978-0-387-95262-8。 OCLC: 722601833。
52. 乔丹，帕斯库尔；泡利，沃尔夫冈（1928）。 "Zur Quantenelektrodynamik ladungsfreier Felder" [关于无电荷场的量子电动力学]。 《物理学杂志》（德文） 第 47 卷（第 3 期），151–173 页。 Bibcode: 1928ZPhy...47..151J. doi: [10.1007/BF02055793](https://doi.org/10.1007/BF02055793)。 S2CID: 120536476。
53. Schweber, Silvan S.（1994）。 QED and the Men Who Made It: Dyson, Feynman, Schwinger and Tomonaga [量子电动力学及其奠基者：戴森、费曼、施温格和汤川]。普林斯顿大学出版社。第 108–112 页。 ISBN: 978-0-691-03327-3。 OCLC: 439849774。
54. 狄拉克（1927）。
55. Weinberg, Steven（1977）。 "The Search for Unity: Notes for a History of Quantum Field Theory" [统一性的探索：量子场论历史笔记]。 《代达罗斯》 第 106 卷（第 4 期），17–35 页。 JSTOR: 20024506。
56. 横山弘；氏原清（1995）。 Spontaneous emission and laser oscillation in microcavities[微腔中的自发辐射和激光振荡]。博卡拉顿：CRC 出版社。第 6 页。 ISBN: 978-0-8493-3786-4。 OCLC: 832589969。
57. Scully & Zubairy（1997）。 §1.5.2 第 22–23 页。
58. 魏斯科普夫，维克托（1935）。 "Probleme der neueren Quantentheorie des Elektrons" [关于电子新量子理论的问题]。 《自然科学》（德文） 第 23 卷（第 37 期），631–637 页。 Bibcode: 1935NW.....23..631W. doi: [10.1007/BF01492012](https://doi.org/10.1007/BF01492012)。 S2CID: 6780937。
59. Welton, Theodore Allen（1948）。 "Some observable effects of the quantum-mechanical fluctuations of the electromagnetic field" [电磁场量子力学波动的一些可观察效应]。 《物理评论》 第 74 卷（第 9 期），1157 页。 Bibcode: 1948PhRv...74.1157W. doi: [10.1103/PhysRev.74.1157](https://doi.org/10.1103/PhysRev.74.1157)。
60. Lamb, Willis; Retherford, Robert（1947）。 "Fine Structure of the Hydrogen Atom by a Microwave Method" [利用微波方法研究氢原子的精细结构]。 《物理评论》 第 72 卷（第 3 期），241–243 页。 Bibcode: 1947PhRv...72..241L. doi: [10.1103/PhysRev.72.241](https://doi.org/10.1103/PhysRev.72.241)。
61. Foley, H.; Kusch, P. (1948). "On the Intrinsic Moment of the Electron" [关于电子的内禀磁矩]。 《物理评论》 第 73 卷（第 3 期），412 页。 Bibcode: 1948PhRv...73..412F. doi: [10.1103/PhysRev.73.412](https://doi.org/10.1103/PhysRev.73.412)。
62. Dresden, M. (1987). H. A. Kramers: Between Tradition and Revolution [H.A. 克拉默斯：传统与革命之间]。 纽约：Springer 出版社。 ISBN: 978-1-461-29087-2。 OCLC: 1015092892。
63. Weisskopf (1936), 第 6 页
64. Bethe, Hans Albrecht (1947). "The Electromagnetic Shift of Energy Levels" [能级的电磁位移]。 《物理评论》 第 72 卷（第 4 期），339 页。 Bibcode: 1947PhRv...72..339B. doi: [10.1103/PhysRev.72.339](https://doi.org/10.1103/PhysRev.72.339)。 S2CID: 120434909。
65. Power (1964), 第 35 页
66. Pauli, Wolfgang (1946). "Exclusion principle and quantum mechanics" [不相容原理与量子力学] (PDF)。 nobelprize.org，瑞典皇家科学院。 [访问于 2016 年 10 月 20 日](https://www.nobelprize.org)。
67. Casimir, Hendrik Brugt Gerhard; Polder, Dirk (1948). "The Influence of Retardation on the London–Van der Waals Forces" [伦敦–范德华力中迟滞的影响]。 《物理评论》 第 73 卷（第 4 期），360 页。 Bibcode: 1948PhRv...73..360C. doi: [10.1103/PhysRev.73.360](https://doi.org/10.1103/PhysRev.73.360)。
68. Casimir, Hendrik Brugt Gerhard (1948). "On the attraction between two perfectly conducting plates" [关于两块完美导电板之间的吸引力] (PDF)。 《荷兰皇家艺术与科学学院学报》 第 51 卷，793–795 页。 [访问于 2016 年 10 月 19 日](https://www.dwc.knaw.nl)。
69. Eisenschitz, R. & London, F. (1930). "Über das Verhältnis der Van der Waalsschen Kräfte zu den homöopolaren Bindungskräften" [范德华力与同极性键合力的关系]。 《物理学杂志》（德文）第 60 卷（第 7–8 期），491–527 页。 Bibcode: 1930ZPhy...60..491E. doi: [10.1007/BF01341258](https://doi.org/10.1007/BF01341258)。 S2CID: 125644826。
70. London, F. (1930). "Zur Theorie und Systematik der Molekularkräfte" [关于分子力的理论与体系]。 《物理学杂志》（德文） 第 63 卷（第 3–4 期），245 页。 Bibcode: 1930ZPhy...63..245L. doi: [10.1007/BF01421741](https://doi.org/10.1007/BF01421741)。 S2CID: 123122363。
71. Lambrecht, Astrid (2002). "The Casimir effect: a force from nothing" [卡西米尔效应：来自虚无的力] (PDF)。 《物理世界》 第 15 卷（第 9 期），物理学会出版社，第 29–32 页。 doi: [10.1088/2058-7058/15/9/29](https://doi.org/10.1088/2058-7058/15/9/29)。 ISSN: 0953-8585。 [访问于 2016 年 10 月 24 日](https://physicsworld.com)。
72. Lifshitz, E. M. (1954). "The Theory of Molecular Attractive Forces between Solids" [固体间分子吸引力理论]。 《苏联实验与理论物理学杂志》第 29 卷，94–110 页。
73. Lifshitz, E. M. (1956). "The theory of molecular Attractive Forces between Solids" [固体间分子吸引力理论]。 《苏联物理学杂志》 第 2 卷（第 1 期），73–83 页。
74. Derjaguin, B. V.; Abrikosova, I. I.; Lifshitz, E. M. (1956). "Direct measurement of molecular attraction between solids separated by a narrow gap" [测量窄间隙中分子吸引力的实验研究]。 《化学学会季刊评论》 第 10 卷（第 3 期），295–329 页。 doi: [10.1039/qr9561000295](https://doi.org/10.1039/qr9561000295)。
75. Mahanty, J.; Ninham, B. W. (1976). Dispersion Forces [色散力]。 Academic Press 出版社。 ISBN: 978-0-124-65050-3。 OCLC: 925046024。
76. Callen, Herbert; Welton, Theodore A. (1951). "Irreversibility and Generalized Noise" [不可逆性与广义噪声]。 《物理评论》 第 83 卷（第 1 期），34–40 页。 Bibcode: 1951PhRv...83...34C。 doi: [10.1103/PhysRev.83.34](https://doi.org/10.1103/PhysRev.83.34)。
77. Nyquist, Harry (1928). "Thermal Agitation of Electric Charge in Conductors" [导体中电荷的热激发]。 《物理评论》 第 32 卷（第 1 期），110–113 页。 Bibcode: 1928PhRv...32..110N。 doi: [10.1103/PhysRev.32.110](https://doi.org/10.1103/PhysRev.32.110)。
78. Johnson, John Bertrand (1928). "Thermal Agitation of Electricity in Conductors" [导体中电流的热激发]。 《物理评论》 第 32 卷（第 1 期），97–109 页。 Bibcode: 1928PhRv...32...97J。 doi: [10.1103/PhysRev.32.97](https://doi.org/10.1103/PhysRev.32.97)。
79. Milonni (1994), 第 54 页
80. Koch, Roger H.; Van Harlingen, D. J.; Clarke, John (1981). "Observation of Zero-Point Fluctuations in a Resistively Shunted Josephson Tunnel Junction" [在电阻性偏置约瑟夫森隧道结中观察到的零点波动] (PDF)。 《物理评论快报》 第 47 卷（第 17 期），1216–1219 页。 Bibcode: 1981PhRvL..47.1216K。 doi: [10.1103/PhysRevLett.47.1216](https://doi.org/10.1103/PhysRevLett.47.1216)。 OSTI: 1136482。 S2CID: 119728862。
81. Allahverdyan, A. E.; Nieuwenhuizen, Th. M. (2000). "Extraction of Work from a Single Thermal Bath in the Quantum Regime" [在量子区域中从单一热浴提取功] (PDF)。 《物理评论快报》 第 85 卷（第 9 期），1799–1802 页。 arXiv: [cond-mat/0006404](https://arxiv.org/abs/cond-mat/0006404)。 Bibcode: 2000PhRvL..85.1799A。 doi: [10.1103/PhysRevLett.85.1799](https://doi.org/10.1103/PhysRevLett.85.1799)。 PMID: 10970617。 S2CID: 32579381。
82. Scully et al. (2003)。
83. Jaynes, E. T.; Cummings, F. W. (1963). "Comparison of quantum and semiclassical radiation theories with application to the beam maser" [量子与半经典辐射理论的比较及其在波束微波放大器中的应用]。 《IEEE 学报》 第 51 卷（第 1 期），89–109 页。 doi: [10.1109/PROC.1963.1664](https://doi.org/10.1109/PROC.1963.1664)。
84. Drexhage (1970)。
85. Drexhage (1974), 第[页码待补充]页。
86. Hulet, Randall G.; Hilfer, Eric S.; Kleppner, Daniel (1985). "Inhibited Spontaneous Emission by a Rydberg Atom" [里德伯原子中受抑制的自发辐射] (PDF)。 《物理评论快报》 第 55 卷（第 20 期），2137–2140 页。 Bibcode: 1985PhRvL..55.2137H。 doi: [10.1103/PhysRevLett.55.2137](https://doi.org/10.1103/PhysRevLett.55.2137)。 hdl: [1911/79433](https://hdl.handle.net/1911/79433)。 PMID: 10032058。
87. Yablonovitch, Eli (1987). "Inhibited Spontaneous Emission in Solid-State Physics and Electronics" [固态物理与电子学中的受抑制自发辐射]。 《物理评论快报》 第 58 卷（第 20 期），2059–2062 页。 Bibcode: 1987PhRvL..58.2059Y。 doi: [10.1103/PhysRevLett.58.2059](https://doi.org/10.1103/PhysRevLett.58.2059)。 PMID: 10034639。
88. Purcell, E. M. (1946). "Proceedings of the American Physical Society" [美国物理学会会议记录]。 《物理评论》 第 69 卷（第 11–12 期），674 页。 Bibcode: 1946PhRv...69Q.674.. doi: [10.1103/PhysRev.69.674](https://doi.org/10.1103/PhysRev.69.674)。
89. Goy et al. (1983)。
90. Milonni (1983)。
91. Heisenberg, Werner (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik" [关于量子理论运动学与力学的直观内容]。 《物理学杂志》（德文） 第 43 卷（第 3 期），172–198 页。 Bibcode: 1927ZPhy...43..172H。 doi: [10.1007/BF01397280](https://doi.org/10.1007/BF01397280)。 S2CID: 122763326。
92. Gribbin, J. R. (1998). Gribbin, M. (编)。 Q is for Quantum: An Encyclopedia of Particle Physics [量子百科：粒子物理学百科全书]。 Touchstone Books 出版社。 Bibcode: 1999qqep.book.....G。 ISBN: 978-0-684-86315-3。 OCLC: 869069919。
93. Peskin & Schroeder (1995), 第 786–791 页。
94. Milonni (1994), 第 73–74 页。
95. Wheeler, John Archibald (1955). "Geons" [引力电子]。 《物理评论》 第 97 卷（第 2 期），511 页。 Bibcode: 1955PhRv...97..511W。 doi: [10.1103/PhysRev.97.511](https://doi.org/10.1103/PhysRev.97.511)。
96. Power (1964), 第 31–33 页。
97. Milonni (1981)。
98. Senitzky, I. R. (1960). "Dissipation in Quantum Mechanics. The Harmonic Oscillator" [量子力学中的耗散现象：简谐振子]。 《物理评论》第 119 卷（第 2 期），670 页。 Bibcode: 1960PhRv..119..670S。 doi: [10.1103/PhysRev.119.670](https://doi.org/10.1103/PhysRev.119.670)。
99. "Higgs bosons: theory and searches" (2012). PDGLive。粒子数据组。 [PDF 版本](https://pdg.lbl.gov)。 [访问于 2012 年 8 月 15 日](https://pdglive.lbl.gov)。
100. Milonni (1994), 第 42–43 页。
101. Peskin & Schroeder (1995), 第 22 页。
102. Milonni (2009), 第 865 页。
103. Abbott, Larry (1988). "The Mystery of the Cosmological Constant" [宇宙学常数之谜] (PDF)。 《科学美国人》 第 258 卷（第 5 期），106–113 页。 Bibcode: 1988SciAm.258e.106A。 doi: [10.1038/scientificamerican0588-106](https://doi.org/10.1038/scientificamerican0588-106)。
104. Derjaguin, B. V.; Abrikosova, I. I.; Lifshitz, E. M. (1956). "Direct measurement of molecular attraction between solids separated by a narrow gap" [测量窄间隙中固体分子吸引力的实验研究]。 《化学学会季刊评论》 第 10 卷（第 3 期），295–329 页。 doi: [10.1039/QR9561000295](https://doi.org/10.1039/QR9561000295)。
105. Sparnaay, M. J. (1958). "Measurements of attractive forces between flat plates" [平板间吸引力的测量]。 《物理学报》 第 24 卷（第 6–10 期），751–764 页。 Bibcode: 1958Phy....24..751S。 doi: [10.1016/S0031-8914(58)80090-7](https://doi.org/10.1016/S0031-8914(58)80090-7)。
106. Tabor, D.; Winterton, R. H. S. (1968). "Surface Forces: Direct Measurement of Normal and Retarded Van der Waals Forces" [表面力：范德华力的直接测量与迟滞影响]。 《自然》 第 219 卷（第 5159 期），1120–1121 页。 Bibcode: 1968Natur.219.1120T。 doi: [10.1038/2191120a0](https://doi.org/10.1038/2191120a0)。 PMID: 5675624。 S2CID: 4258508。
107. Hunklinger, S.; Geisselmann, H.; Arnold, W. (1972). "A Dynamic Method for Measuring the Van der Waals Forces between Macroscopic Bodies" [测量宏观物体间范德华力的动态方法]。 《科学仪器评论》 第 43 卷（第 4 期），584–587 页。 Bibcode: 1972RScI...43..584H。 doi: [10.1063/1.1685696](https://doi.org/10.1063/1.1685696)。
108. Van Blokland, Peter H. G. M.; Overbeek, J. Theodoor G. (1978). "Van der Waals forces between objects covered with a chromium layer" [铬涂层物体间的范德华力]。 《化学学会法拉第转让杂志 1》第 74 卷，2637–2651 页。 doi: [10.1039/F19787402637](https://doi.org/10.1039/F19787402637)。
109. Lamoreaux, S. K. (1997). "Demonstration of the Casimir Force in the 0.6 to 6 μm Range" [在 0.6 至 6 微米范围内的卡西米尔力演示] (PDF)。 《物理评论快报》 第 78 卷（第 1 期），5–8 页。 Bibcode: 1997PhRvL..78....5L。 doi: [10.1103/PhysRevLett.78.5](https://doi.org/10.1103/PhysRevLett.78.5)。
110. Mohideen, Umar; Roy, Anushree (1998). "Precision Measurement of the Casimir Force from 0.1 to 0.9 μm" [在 0.1 至 0.9 微米范围内的卡西米尔力精密测量]。 《物理评论快报》 第 81 卷（第 21 期），4549–4552 页。 arXiv: [physics/9805038](https://arxiv.org/abs/physics/9805038)。 Bibcode: 1998PhRvL..81.4549M。 doi: [10.1103/PhysRevLett.81.4549](https://doi.org/10.1103/PhysRevLett.81.4549)。 S2CID: 56132451。
111. Chan et al. (2001).
112. Bressi et al. (2002).
113. Decca et al. (2003).
114. Munday, J. N.; Capasso, Federico; Parsegian, V. Adrian (2009). "Measured long-range repulsive Casimir–Lifshitz forces" [长距离排斥型卡西米尔-利夫希茨力的测量] (PDF)。 《自然》 第 457 卷（第 7226 期），170–173 页。 Bibcode: 2009Natur.457..170M。 doi: [10.1038/nature07610](https://doi.org/10.1038/nature07610)。 PMC: 4169270。 PMID: 19129843。
115. Dzyaloshinskii, I. E.; Lifshitz, E. M.; Pitaevskii, Lev P. (1961). "General Theory of Van der Waals' Forces" [范德华力的一般理论]。 《苏联物理学进展》 第 4 卷（第 2 期），154 页。 Bibcode: 1961SvPhU...4..153D。 doi: [10.1070/PU1961v004n02ABEH003330](https://doi.org/10.1070/PU1961v004n02ABEH003330)。
116. Capasso et al. (2007).
117. See Barton & Scharnhorst (1993) and Chown (1990).
118. Itzykson & Zuber (1980), 第 80 页。
119. Hawton, M. (1993). "Self-consistent frequencies of the electron–photon system" [电子-光子系统的自洽频率]。 《物理评论 A》 第 48 卷（第 3 期），1824–1831 页。 Bibcode: 1993PhRvA..48.1824H。 doi: [10.1103/PhysRevA.48.1824](https://doi.org/10.1103/PhysRevA.48.1824)。 PMID: 9909797。
120. Le Bellac (2006), 第 381 页。
121. Le Bellac (2006), 第 33 页。
122. Aitchison, Ian; Hey, Anthony (2012). Gauge Theories in Particle Physics: A Practical Introduction: Volume 1: From Relativistic Quantum Mechanics to QED (4th ed.)[粒子物理中的规范理论：实用导论，第 1 卷，从相对论量子力学到量子电动力学（第 4 版）]。 CRC 出版社，第 343 页。 ISBN: 9781466512993。
123. Quigg, C (1998). Espriu, D.; Pich, A. (编)。 Advanced School on Electroweak Theory: Hadron Colliders, the Top Quark, and the Higgs Sector[电弱理论高级课程：强子对撞机、顶夸克与希格斯部门]。 World Scientific 出版社，第 143 页。 ISBN: 9789814545143。
124. Heisenberg & Euler (1936)。
125. Weisskopf (1936), 第 3 页。
126. Greiner, Müller & Rafelski (2012), 第 278 页。
127. Greiner, Müller & Rafelski (2012), 第 291 页。
128. See Dunne (2012)** [参见 Dunne (2012)] for a historical review of the subject [获取该主题的历史综述]。
129. Heyl & Shaviv (2000), 第 1 页。
130. See Carroll & Field (1997) and Kostelecký and Mewes (2009, 2013)** [参见 Carroll & Field (1997) 和 Kostelecký and Mewes (2009, 2013)] for an overview of this area [获取该领域的概述]。
131. See Mignani et al. (2017) for experiment [参见 Mignani 等人（2017）的实验]， and Cho (2016), Crane (2016) and Bennett (2016)for comment [以及 Cho (2016), Crane (2016), Bennett (2016) 的评论]。
132. Rees (2012), 第 528 页。
133. Crane (2016)。
134. Cho (2016)。
135. Battersby (2016)。
136. Riess et al. (1998)。
137. Perlmutter et al. (1998)。
138. Clark, Stuart (2016). "The Universe is Flat as a Pancake" [宇宙像煎饼一样平坦]。 《新科学家》第 232 卷，第 3097 期，第 35 页。
139. Miller, Katrina (2023 年 7 月 1 日). "The Dark Universe Is Waiting. What Will the Euclid Telescope Reveal?" [暗宇宙正在等待，欧几里得望远镜将揭示什么？]。 《纽约时报》。 [访问于 2023 年 8 月 23 日](https://www.nytimes.com)。
140. Carroll, Sean M. (1998). "Quintessence and the Rest of the World: Suppressing Long-Range Interactions" [第五元素与世界其他部分：抑制长距离相互作用] (PDF)。 《物理评论快报》 第 81 卷（第 15 期），3067–3070 页。 arXiv: [astro-ph/9806099](https://arxiv.org/abs/astro-ph/9806099)。 Bibcode: 1998PhRvL..81.3067C。 doi: [10.1103/PhysRevLett.81.3067](https://doi.org/10.1103/PhysRevLett.81.3067)。 ISSN: 0031-9007。 S2CID: 14539052。
141. Tyson, Neil deGrasse and Donald Goldsmith (2004). Origins: Fourteen Billion Years of Cosmic Evolution [起源：140 亿年的宇宙演化]。 W. W. Norton & Company，第 84–85 页。
142. Wesson, Paul S. "Cosmological constraints on the zero-point electromagnetic field" [零点电磁场的宇宙学约束]。 《天体物理学杂志》，Part 1，第 378 卷，1991 年 9 月 10 日，466–470 页。由 NSERC 资助的研究。
143. Enz, Charles P. (1974). Enz, C. P.; Mehra, J. (编)。 Physical Reality and Mathematical Description: Is the Zero-Point Energy Real? [物理现实与数学描述：零点能量是否真实？]。 Dordrecht: D. Reidel Publishing Company，第 124–132 页。 doi: [10.1007/978-94-010-2274-3](https://doi.org/10.1007/978-94-010-2274-3)。 ISBN: 978-94-010-2274-3。 S2CID: 118779716。
144. See Schwinger (1998a, 1998b, 1998c).
145. Schwinger, Julian (1975). "Casimir effect in source theory" [源理论中的卡西米尔效应]。 《数学物理通讯》 第 1 卷（第 1 期），43–47 页。 Bibcode: 1975LMaPh...1...43S。 doi: [10.1007/BF00405585](https://doi.org/10.1007/BF00405585)。 S2CID: 126297065。
146. Schwinger, Julian; DeRaad, Lester L.; Milton, Kimball A. (1978). "Casimir effect in dielectrics" [介质中的卡西米尔效应]。 《物理年鉴》 第 115 卷（第 1 期），1–23 页。 Bibcode: 1978AnPhy.115....1S。 doi: [10.1016/0003-4916(78)90172-0](https://doi.org/10.1016/0003-4916(78)90172-0)。
147. Jaffe, R. L. (2005). "Casimir effect and the quantum vacuum" [卡西米尔效应与量子真空]。 《物理评论 D》 第 72 卷（第 2 期），021301 页。 arXiv: [hep-th/0503158](https://arxiv.org/abs/hep-th/0503158)。 Bibcode: 2005PhRvD..72b1301J。 doi: [10.1103/PhysRevD.72.021301](https://doi.org/10.1103/PhysRevD.72.021301)。 S2CID: 13171179。
148. Milonni (1994), 第 48 页。
149. Greiner, Müller & Rafelski (2012), 第 20 页。
150. Barrett, Terence W. (2008). Topological Foundations of Electromagnetism [电磁学的拓扑基础]。 新加坡：World Scientific 出版社，第 2 页。 ISBN: 9789812779977。
151. Greiner, Müller & Rafelski (2012), 第 23 页。
152. Ehrenberg, W.; Siday, R. E. (1949). "The Refractive Index in Electron Optics and the Principles of Dynamics" [电子光学中的折射率与动力学原理]。 《物理学会会议》系列 B 第 62 卷（第 1 期），8–21 页。 Bibcode: 1949PPSB...62....8E。 doi: [10.1088/0370-1301/62/1/303](https://doi.org/10.1088/0370-1301/62/1/303)。
153. Aharonov, Y.; Bohm, D. (1959). "Significance of electromagnetic potentials in quantum theory" [电磁势在量子理论中的意义]。 《物理评论》 第 115 卷（第 3 期），485–491 页。 arXiv: [1911.10555](https://arxiv.org/abs/1911.10555)。 Bibcode: 1959PhRv..115..485A。 doi: [10.1103/PhysRev.115.485](https://doi.org/10.1103/PhysRev.115.485)。 S2CID: 121421318。
154. Altshuler, B. L.; Aronov, A. G.; Spivak, B. Z. (1981). "The Aaronov-Bohm effect in disordered conductors" [无序导体中的阿哈罗诺夫-玻姆效应] (PDF)。 《苏联实验与理论物理快报》第 33 卷：101 页。 Bibcode: 1981JETPL..33...94A。 原文 (PDF) 存档于 2016 年 11 月 4 日。
155. Berry, M. V. (1984). "Quantal Phase Factors Accompanying Adiabatic Changes" [伴随绝热变化的量子相因子]。 《皇家学会会议》A392 卷（第 1802 期），45–57 页。 Bibcode: 1984RSPSA.392...45B。 doi: [10.1098/rspa.1984.0023](https://doi.org/10.1098/rspa.1984.0023)。
156. Aharonov, Y.; Anandan, J. (1987). "Phase change during a cyclic quantum evolution" [循环量子演化中的相位变化]。 《物理评论快报》 第 58 卷（第 16 期），1593–1596 页。 Bibcode: 1987PhRvL..58.1593A。 doi: [10.1103/PhysRevLett.58.1593](https://doi.org/10.1103/PhysRevLett.58.1593)。 PMID: 10034484。
157. Pancharatnam, S. (1956). "Generalized theory of interference, and its applications" [干涉的广义理论及其应用]。 《印度科学院会议》第 44 卷（第 5 期），247–262 页。 doi: [10.1007/BF03046050](https://doi.org/10.1007/BF03046050)。 S2CID: 118184376。
158. Chiao, Raymond Y.; Wu, Yong-Shi (1986). "Manifestations of Berry's Topological Phase for the Photon" [光子的贝里拓扑相的表现]。 《物理评论快报》 第 57 卷（第 8 期），933–936 页。 Bibcode: 1986PhRvL..57..933C。 doi: [10.1103/PhysRevLett.57.933](https://doi.org/10.1103/PhysRevLett.57.933)。 PMID: 10034203。
159. Josephson, B. D. (1962). "Possible new effects in superconductive tunnelling" [超导隧穿中可能的新效应]。 《物理通讯》第 1 卷（第 7 期），251–253 页。 Bibcode: 1962PhL.....1..251J。 doi: [10.1016/0031-9163(62)91369-0](https://doi.org/10.1016/0031-9163(62)91369-0)。
160. B. D. Josephson (1974). "The discovery of tunnelling supercurrents" [隧道超电流的发现]。 《现代物理评论》第 46 卷（第 2 期），251–254 页。 Bibcode: 1974RvMP...46..251J。 doi: [10.1103/RevModPhys.46.251](https://doi.org/10.1103/RevModPhys.46.251)。
161. K. v. Klitzing; G. Dorda; M. Pepper (1980). "New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance" 《物理评论快报》第 45 卷（第 6 期），494–497 页。 Bibcode: 1980PhRvL..45..494K。 doi: [10.1103/PhysRevLett.45.494](https://doi.org/10.1103/PhysRevLett.45.494)。
162. De Haas, W. J.; Van Alphen, P. M. (1930). "The dependence of the susceptibility of diamagnetic metals upon the field" 《荷兰皇家科学院会议论文集》 第 33 卷：1106 页。
163. Penrose (2004), 第 453–454 页。
164. Feng, J. H.; Kneubühl, F. K. (1995). Barrett, Terence William; Grimes, Dale M. (编)。 《周期性非线性光学介质和激光中的孤子与混沌：高级电磁学：基础、理论与应用》。 新加坡：World Scientific 出版社，第 438 页。 ISBN: 978-981-02-2095-2。
165. Hunt, Bruce J. (2005). 《麦克斯韦学派》。 康奈尔大学出版社，第 17 页。 ISBN: 9780801482342。
166. Josephs, H. J. (1959). "The Heaviside papers found at Paignton in 1957" 《IEE 会议论文集—C 部分：专著》第 106 卷（第 9 期）：70 页。 doi: [10.1049/pi-c.1959.0012](https://doi.org/10.1049/pi-c.1959.0012)。
167. Hunt, Bruce J. (2005). 《麦克斯韦学派》。 康奈尔大学出版社，第 165–166 页。 ISBN: 9780801482342。
168. Barrett, T. W. (1991). "Tesla's Nonlinear Oscillator-Shuttle-Circuit (OSC) Theory" [特斯拉非线性振荡器-摆动电路理论] (PDF)。 《路易·德布罗意基金会年刊》 第 16 卷（第 1 期）：23–41 页。 ISSN: 0182-4295。 原文 (PDF) 存档于 2016 年 9 月 13 日。
169. Penrose (2004), 第 201 页。
170. Rocher, E. Y. (1972). "Noumenon: Elementary entity of a new mechanics" 《数学物理学杂志》 第 13 卷（第 12 期）：1919 页。 Bibcode: 1972JMP....13.1919R。 doi: [10.1063/1.1665933](https://doi.org/10.1063/1.1665933)。
171. Imaeda, K. (1976). "A new formulation of classical electrodynamics" 《新物理 B》 第 32 卷（第 1 期）：138–162 页。 Bibcode: 1976NCimB..32..138I。 doi: [10.1007/BF02726749](https://doi.org/10.1007/BF02726749)。 S2CID: 123315936。
172. Kauffmann, T.; Sun, Wen IyJ (1993). "Quaternion mechanics and electromagnetism" [四元数力学与电磁学]。 《路易·德布罗意基金会年刊》 第 18 卷（第 2 期）：213–219 页。
173. Lambek, Joachim. "QUATERNIONS AND THREE TEMPORAL DIMENSIONS" [四元数与三个时间维度] (PDF)。
174. Bostick et al. (1966).
175. Ferraro, V.; Plumpton, C. (1961). 《磁流体力学导论》。 牛津大学出版社。
176. White, Carol (1977). 《能量潜能：迈向一种新的电磁场理论》。 纽约：Campaigner 出版社。 ISBN: 978-0918388049。
177. Noether, E. (1918). "Invariante Variationsprobleme" [不变变化问题]。 《哥廷根皇家科学院数学-物理学组通讯》 1918 年：235–257 页。
178. Scott (2006), 第 163 页。
179. Pismen, L. M. (2006). 《耗散动力学中的模式与界面》。 Springer 出版社，第 3 页。 ISBN: 9783540304319。
180. The Nobel Foundation (1977). "The Nobel Prize in Chemistry 1977" [1977 年诺贝尔化学奖]。 [诺贝尔奖官方网站](https://www.nobelprize.org)。 瑞典皇家科学院。
181. 尼科利斯 (Nicolis, G.) 和普里戈金 (Prigogine, I.)（1977 年）。《非平衡系统中的自组织：从耗散结构到通过波动的秩序》（Self-organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations）。Wiley-Blackwell 出版社。ISBN 978-0471024019。
182. 伊利亚·普里戈金 (Ilya Prigogine) 和伊莎贝尔·斯腾格斯 (Isabelle Stengers)（1984 年）。《从混乱中产生秩序》（Order out of Chaos）。Flamingo 出版社。ISBN 978-0-00-654115-8。
183. 詹姆斯·格雷克 (James Gleick)（1987 年）。《混沌：创建一门新科学》（Chaos: Making a New Science）（1998 年版）。Vintage 出版社。第 308 页。ISBN 9780749386061。
184. 埃里克·J·蔡森 (Eric J. Chaisson)（2002 年）。《宇宙演化：自然中复杂性的崛起》（Cosmic Evolution: The Rise of Complexity in Nature）。哈佛大学出版社。第 139 页。ISBN 978-0674009875。
185. 萨布雷·凯斯 (Sabre Kais)（2011 年）。保罗·波佩利尔 (Paul Popelier) 编。《薛定谔方程关键性的有限尺寸标度：解决薛定谔方程：是否已经尝试了一切？》（Finite Size Scaling for Criticality of the Schrödinger Equation: Solving the Schrödinger Equation: Has Everything Been Tried?）。新加坡：帝国理工学院出版社。第 91-92 页。ISBN 978-1-84816-724-7。
186. 《经典物理学的回归》（"Classical Physics Makes a Comeback"）。《泰晤士报》（The Times）。伦敦。1982 年 1 月 14 日。
187. 博斯蒂克 (W. Bostick)（1985 年）。《关于等离子体等经典系统是否可以表现为超导体（传统认为完全由量子力学主导）的争论》（On the Controversy over Whether Classical Systems Like Plasmas Can Behave Like Superconductors (Which Have Heretofore Been Supposed to Be Strictly Quantum Mechanically Dominated)）(PDF)。国际聚变能量期刊（International Journal of Fusion Energy）。第 3 卷，第 2 期：47–51。PDF 于 2016 年 4 月 3 日存档。2020 年 5 月 22 日检索。
188. 博斯蒂克 (W. Bostick)（1985 年）。《电子形态学》（The Morphology of the Electron）(PDF)。国际聚变能量期刊（International Journal of Fusion Energy）。第 3 卷，第 1 期：9–52。PDF 于 2016 年 4 月 3 日存档。2020 年 5 月 22 日检索。
189. 博斯蒂克 (W. Bostick)（1985 年）。《达姆施塔特德国西部等离子聚焦小组最近的实验结果：回顾与评论》（Recent Experimental Results of The Plasma-Focus Group at Darmstadt, West Germany: A Review and Critique）(PDF)。国际聚变能量期刊（International Journal of Fusion Energy）。第 3 卷，第 1 期：68。PDF 于 2016 年 4 月 3 日存档。2020 年 5 月 22 日检索。
190. W. 法瑞尔·爱德华兹 (W. Farrell Edwards)（1981 年）。《伦敦方程的经典推导》（Classical Derivation of the London Equations）。《物理评论快报》（Physical Review Letters）。第 47 卷，第 26 期：1863–1866。Bibcode:1981PhRvL..47.1863E。doi:10.1103/PhysRevLett.47.1863。
191. 弗里利希 (Fröhlich, H.)（1966）。《超导体中的宏观波函数》（"Macroscopic wave functions in superconductors"）。《物理学会会刊》（Proceedings of the Physical Society）。87（1）：330–332。Bibcode:1966PPS....87..330F。doi:10.1088/0370-1328/87/1/137。
192. 里德 (Reed)（1995），第 226 页。
193. 陈谐 (Chen, Xie)，顾正成 (Gu, Zheng-Cheng)，温晓刚 (Wen, Xiao-Gang)（2010）。《局部幺正变换、长程量子纠缠、波函数重整化和拓扑有序》（"Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order"）。《物理评论 B》（Physical Review B）。82（15）：155138。arXiv:1004.3835。Bibcode:2010PhRvB..82o5138C。doi:10.1103/PhysRevB.82.155138。S2CID 14593420。
194. 埃里克·J·蔡森 (Eric J. Chaisson)（2005）。《能源丰富的宇宙中的非平衡热力学》（"Non-equilibrium Thermodynamics in an Energy-Rich Universe"）。《理解复杂系统》（Understanding Complex Systems）。第 21–31 页。doi:10.1007/11672906_2。ISBN 978-3-540-22495-2。
195. 埃里克·J·蔡森 (Eric J. Chaisson)（2002）。《宇宙演化：自然中复杂性的崛起》（Cosmic Evolution: The Rise of Complexity in Nature）。哈佛大学出版社，第 216 页。ISBN 978-0674009875。
196. 彼得森 (Peterson, I.)（1997）。《窥探电子屏障》（"Peeking inside an electron's screen"）。《科学新闻》（Science News）。151：89。检索日期：2016 年 10 月 24 日。
197. 安伯·M·艾肯 (Amber M. Aiken)。《零点能：我们能否从无中生有？》（"Zero-Point Energy: Can We Get Something From Nothing?"）。美国陆军国家地面情报中心（U.S. Army National Ground Intelligence Center）。零点能与 “自由能源” 发明及永动机的研究被更广泛的科学界视为伪科学。
198. 《零点能》，第八季第二集。《科学美国人前沿》（Scientific American Frontiers）。Chedd-Angier 制作公司。1997–1998。PBS。2006 年 1 月 1 日存档。
199. 斯科特 (Scott)（2004）。
200. 罗伯特·L·福沃德 (Robert L. Forward)（1985）。《通过带电箔状导体的粘附从真空中提取电能》（"Extracting electrical energy from the vacuum by cohesion of charged foliated conductors"）。《物理评论 B》（Physical Review B）。30（4）：1700。Bibcode:1984PhRvB..30.1700F。doi:10.1103/PhysRevB.30.1700。
201. 平托 (Pinto)（1999）。
202. 斯坎杜拉 (Scandurra, M.)（2001）。《量子真空的热力学性质》（"Thermodynamic properties of the quantum vacuum"）。arXiv:hep-th/0104127。
203. 加雷特·莫德尔 (Garret Moddel) 和 **奥尔加·德米特里耶娃 (Olga Dmitriyevaa)**（2009）。《从真空中提取零点能：基于随机电动力学方法的评估与其他方法的比较》（"Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods"）。《原子》（Atoms）。7（2）：51。arXiv:0910.5893。doi:10.3390/atoms7020051。S2CID 17095906。
204. 《真空研究：DARPA 尝试利用难以捉摸的卡西米尔效应实现突破技术》（"Research in a Vacuum: DARPA Tries to Tap Elusive Casimir Effect for Breakthrough Technology"）。www.scientificamerican.com。科学美国人（Scientific American）。2008 年。检索日期：2024 年 2 月 22 日。
205. 美国专利 7,379,286。
206. 奥尔加·德米特里耶娃 (Olga Dmitriyevaa)和 **加雷特·莫德尔 (Garret Moddel)**（2012）。《测试从通过卡西米尔空腔流动的气体中发射零点能》（"Test of zero-point energy emission from gases flowing through Casimir cavities"）(PDF)。《物理学会议录》（Physics Procedia）。38：8–17。Bibcode:2012PhPro..38....8D。doi:10.1016/j.phpro.2012.08.007。PDF 于 2021 年 5 月 7 日存档。2016 年 11 月 1 日检索。
207. 卡洛斯·恩里克斯 (Carlos Henriques)（2014）。《卡西米尔空腔引起的原子能量偏移研究》（Study of atomic energy shifts induced by Casimir cavities）（硕士论文）。导师：路易斯·费尔南德斯 (Luis Fernandes) 和 F·阿马罗 (F. Amaro)。doi:10.13140/RG.2.1.4297.1608。
208. 麦克唐纳 (D. K. C. MacDonald)（1962）。《关于布朗运动和不可逆性》（"On Brownian Movement and irreversibility"）。《物理学》（Physica）。28（4）：409–416。Bibcode:1962Phy....28..409M。doi:10.1016/0031-8914(62)90019-8。
209. 哈里斯 (I. A. Harris)（1971）。《零点波动和热噪声标准》（"Zero-point fluctuations and thermal-noise standards"）。《电子快报》（Electron. Lett.）。7（7）：148–149。Bibcode:1971ElL.....7..148H。doi:10.1049/el:19710095。
210. Grau, G.; Kleen, W.（1982）。《关于零点能、量子噪声和自发发射噪声的评论》（"Comments on zero-point energy, quantum noise and spontaneous-emission noise"）。《固态电子学》（Solid-State Electronics）。25（8）：749–751。Bibcode:1982SSEle..25..749G。doi:10.1016/0038-1101(82)90204-0。
211. Kleen, W.（1985）。《热噪声和零点能》（"Thermal noise and zero-point-energy"）。《物理系统中的噪声和 1/F 噪声 1985》（Noise in Physical Systems and 1/F Noise 1985）。第 331–332 页。doi:10.1016/B978-0-444-86992-0.50072-2。ISBN 9780444869920。
212. Kiss, L. B.（1988）。《关于零点能和热噪声问题》（"To the problem of zero-point energy and thermal noise"）。《固态通讯》（Solid State Communications）。67（7）：749–751。Bibcode:1988SSCom..67..749K。doi:10.1016/0038-1098(88)91020-4。
213. Abbott 等人（1996）。
214. Scully（2001）。
215. Galve, Fernando; Lutz, Eric（2009）。《挤压的非平衡热力学分析》（"Nonequilibrium thermodynamic analysis of squeezing"）。《物理评论 A》（Physical Review A）。79（5）：055804。Bibcode:2009PhRvA..79e5804G。doi:10.1103/PhysRevA.79.055804。
216. Dillenschneider, R.; Lutz, E.（2009）。《量子关联的能量学》（"Energetics of quantum correlations"）。《欧洲物理快报》（EPL）。88（5）：50003。arXiv:0803.4067。Bibcode:2009EL.....8850003D。doi:10.1209/0295-5075/88/50003。S2CID 119262651。
217. Huang, X. L.; Wang, Tao; Yi, X. X.（2012）。《储能库挤压对量子系统和能量提取的影响》（"Effects of reservoir squeezing on quantum systems and work extraction"）。《物理评论 E》（Physical Review E）。86（5）：051105。Bibcode:2012PhRvE..86e1105H。doi:10.1103/PhysRevE.86.051105。PMID 23214736。
218. Boukobza, E.; Ritsch, H.（2013）。《不违反第二定律突破卡诺极限：离共振量子光生成的热力学分析》（"Breaking the Carnot limit without violating the second law: A thermodynamic analysis of off-resonant quantum light generation"）。《物理评论 A》（Physical Review A）。87（6）：063845。Bibcode:2013PhRvA..87f3845B。doi:10.1103/PhysRevA.87.063845。
219. Roßnagel 等人（2014）。
220. Correa 等人（2014）。
221. Abah, Obinna; Lutz, Eric（2014）。《耦合非平衡储能库的热机效率》（"Efficiency of heat engines coupled to nonequilibrium reservoirs"）。《欧洲物理快报》（EPL）。106（2）：20001。arXiv:1303.6558。Bibcode:2014EL....10620001A。doi:10.1209/0295-5075/106/20001。S2CID 118468331。
222. Gardas, Bartłomiej; Deffner, Sebastian; Saxena, Avadh（2016）。《非厄米量子热力学》（"Non-hermitian quantum thermodynamics"）。《科学报告》（Scientific Reports）。6：23408。arXiv:1511.06256。Bibcode:2016NatSR...623408G。doi:10.1038/srep23408。PMC 4802220。PMID 27003686。
223. Gemmer, Jochen; Michel, M.; Mahler, Günter (2009)。《量子热力学：复合量子系统中热力学行为的出现》（Quantum Thermodynamics: Emergence of Thermodynamic Behavior Within Composite Quantum Systems）。Springer。doi:10.1007/978-3-540-70510-9。ISBN 978-3-540-70510-9。
224. Noever, David; Bremner, Christopher (1999)。《大规模萨哈罗夫条件》（"Large-scale Sakharov condition"）。AIAA 第 35 届联合推进会议与展览（AIAA 35th Joint Propulsion Conference and Exhibit）。doi:10.2514/6.1999-2146。
225. Haisch, B.; Rueda, A.; Dobyns, Y. (2001)。《惯性质量与量子真空场》（"Inertial mass and the quantum vacuum fields"）。《物理年鉴》（Annalen der Physik）。10（5）：393–414。arXiv:gr-qc/0009036。Bibcode:2001AnP...513..393H。doi:10.1002/1521-3889(200105)10:5<393::AID-ANDP393>3.0.CO;2-Z。S2CID 15382105。
226. Podkletnov, Evgeny; Modanese, Giovanni(2001)。《基于复合晶体结构的带电 YBa2Cu3O7−y 超导体的冲量引力发生器》（"Impulse Gravity Generator Based on Charged YBa2Cu3O7−y Superconductor with Composite Crystal Structure"）。arXiv:physics/0108005。
227. Matthews, Robert (1996 年 9 月 21 日)。《反重力装置因争议而步履维艰》（"Antigravity machine weighed down by controversy"）。《新科学家》（New Scientist）。检索日期：2016 年 10 月 26 日。
228. Lano, R. P. (1996)。《引力迈斯纳效应》（"Gravitational Meissner Effect"）。arXiv:hep-th/9603077。
229. Forward, R. L. (1963)。《反重力指南》（"Guidelines to Antigravity"）。《美国物理学杂志》（American Journal of Physics）。31（3）：166–170。Bibcode:1963AmJPh..31..166F。doi:10.1119/1.1969340。
230. Forward, R. L. (1961)。《实验物理学家的广义相对论》（"General Relativity for the Experimentalist"）。《IRE 会议论文集》（Proceedings of the IRE）。49（5）：892–904。Bibcode:1961PIRE...49..892F。doi:10.1109/JRPROC.1961.287932。S2CID 51650940。
231. Swain, John (2010)。《电力变压器的引力磁学类比》（"Gravitatomagnetic Analogs of Electric Transformers"）。arXiv:1006.5754 [gr-qc]。
232. 《物理学家预测电力变压器的引力类比》（"Physicist Predicts Gravitational Analogue Of Electrical Transformers"）。MIT 科技评论（MIT Technology Review）。2010 年 7 月 6 日。检索日期：2016 年 10 月 28 日。
233. DeWitt, Bryce S. (1966)。《超导体与引力拖拽》（"Superconductors and Gravitational Drag"）。《物理评论快报》（Physical Review Letters）。16（24）：1092–1093。Bibcode:1966PhRvL..16.1092D。doi:10.1103/PhysRevLett.16.1092。
234. Ross, D. K. (1983)。《引力场中超导体的伦敦方程》（"The London equations for superconductors in a gravitational field"）。《物理学杂志 A》（Journal of Physics A）。16（6）：1331–1335。Bibcode:1983JPhA...16.1331R。doi:10.1088/0305-4470/16/6/026。
235. 美国专利 3,626,606。
236. 美国专利 3,626,605。
237. 美国专利 3,823,570。
238. Barker, B. M.; O'Connell, R. F. (1979)。《引力相互作用：自旋、旋转与量子效应综述》（"The gravitational interaction: Spin, rotation, and quantum effects-a review"）。《广义相对论与引力》（General Relativity and Gravitation）。11（2）：149–175。Bibcode:1979GReGr..11..149B。doi:10.1007/BF00756587。S2CID 121728055。
239. O'Connell, R. F. (1970)。《电子的引力场》（"The gravitational field of the electron"）。《物理学快报 A》（Physics Letters A）。32（6）：402–403。Bibcode:1970PhLA...32..402O。doi:10.1016/0375-9601(70)90022-8。
240. O'Connell, R. F.; Rasband, S. N. (1971)。《圆盘与圆柱之间的伦斯-提林型引力作用力》（"Lense-Thirring Type Gravitational Forces Between Disks and Cylinders"）。《自然》（Nature）。232（35）：193–195。Bibcode:1971NPhS..232..193O。doi:10.1038/physci232193a0。
241. Peres, Asher (1978)。《粒子自旋等效原理测试》（"Test of equivalence principle for particles with spin"）。《物理评论 D》（Physical Review D）。18（8）：2739–2740。Bibcode:1978PhRvD..18.2739P。doi:10.1103/PhysRevD.18.2739。
242. Obukhov, Yuri N. (2001)。《自旋、引力与惯性》（"Spin, gravity, and inertia"）。《物理评论快报》（Physical Review Letters）。86（2）：192–195。arXiv:gr-qc/0012102。Bibcode:2001PhRvL..86..192O。doi:10.1103/PhysRevLett.86.192。PMID 11177789。S2CID 35509153。
243. Ritter, R. C.; Winkler, L. I.; Gillies, G. T. (1993)。《通过极化质量扭摆寻找异常自旋依赖力》（"Search for anomalous spin-dependent forces with a polarized-mass torsion pendulum"）。《物理评论快报》（Physical Review Letters）。70（6）：701–704。Bibcode:1993PhRvL..70..701R。doi:10.1103/PhysRevLett.70.701。PMID 10054182。
244. 《反重力不再显得荒谬》（"Antigravity Not So Crazy After All"）。《专利评论》（Patents Review）。《新科学家》（New Scientist）。卷 85，第 1194 期。1980 年 2 月 14 日，第 485 页。
245. Cravens, D. L. (1990)。《电推进研究：最终报告》（"Electric Propulsion Study: Final Report"）。合同编号 F04611-88-C-0014，美国空军航天技术中心宇航实验室（Astronautics Laboratory, AFSC, Air Force Space Technology Center, Space Systems Division, Edwards AFB, CA）。存档自 2011 年 8 月 12 日，检索日期 2016 年 10 月 26 日。
246. Allen, J. E. (2005)。《航空学-1903；航天学-2003；？？2103》（"Aeronautics-1903; aerospace-2003; ? ? 2103"）。《机械工程师学会 G 部分：航空工程期刊》（Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering）。219（3）：235–260。doi:10.1243/095441005X30252。S2CID 110771631。
247. Thorne, Kip; Michael Morris; Ulvi Yurtsever (1988)。《虫洞、时间机器与弱能量条件》（"Wormholes, Time Machines, and the Weak Energy Condition"）。《物理评论快报》（Physical Review Letters）。61（13）：1446–1449。Bibcode:1988PhRvL..61.1446M。doi:10.1103/PhysRevLett.61.1446。PMID 10038800。
248. Wheeler, J Craig (2007)。《宇宙灾难》（Cosmic Catastrophes）（第二版）。纽约：剑桥大学出版社。第 228 页。ISBN 978-0521857147。
249. Alcubierre, Miguel (1994)。《曲速驱动：广义相对论中的超快旅行》（"The warp drive: hyper-fast travel within general relativity"）。《经典与量子引力》（Classical and Quantum Gravity）。11（5）：L73–L77。arXiv:gr-qc/0009013。Bibcode:1994CQGra..11L..73A。doi:10.1088/0264-9381/11/5/001。S2CID 4797900。
250. Podkletnov, E.; Nieminen, R. (1992)。《体积 YBa2Cu3O7−x 超导体可能的引力力屏蔽效应》（"A possibility of gravitational force shielding by bulk YBa2Cu3O7−x superconductor"）。《物理学 C：超导》（Physica C: Superconductivity）。203（3–4）：441–444。Bibcode:1992PhyC..203..441P。doi:10.1016/0921-4534(92)90055-H。
251. Rounds, Frederic N. (1998)。《YBa2Cu3O7 化合物在低温下的异常重量行为》（"Anomalous Weight Behavior in YBa2Cu3O7 Compounds at Low Temperature"）。《NASA 突破推进物理学研讨会论文集》（Proc. NASA Breakthrough Propulsion Phys. Workshop）。279：physics/9705043。arXiv:physics/9705043。Bibcode:1997physics...5043R。
252. Woods et al. (2001)。
253. Tajmar, M.; Plesescu, F.; Marhold, K. & de Matos, C. J. (2006)。《引力磁伦敦效应的实验检测》（"Experimental Detection of the Gravitomagnetic London Moment"）。arXiv:gr-qc/0603033v1。
254. Robertson, Glen A. (1999)。《使用 II 型超导体的引力效应机制》（"On the Mechanism for a Gravity Effect using Type II Superconductors"）。NASA 技术报告服务器（NASA Technical Reports Server）。检索日期：2016 年 10 月 26 日。
255. Li, N.; Torr, D. G.(1991)。《引力磁场对纯超导体的影响》（"Effects of a gravitomagnetic field on pure superconductors"）。《物理评论 D》（Physical Review D）。43（2）：457–459。Bibcode:1991PhRvD..43..457L。doi:10.1103/PhysRevD.43.457。PMID 10013404。
256. Li, Ning; Torr, D. G. (1992)。《引力对超导体磁衰减的影响》（"Gravitational effects on the magnetic attenuation of superconductors"）。《物理评论 B》（Physical Review B）。46（9）：5489–5495。Bibcode:1992PhRvB..46.5489L。doi:10.1103/PhysRevB.46.5489。PMID 10004334。
257. Torr, Douglas G.; Li, Ning (1993)。《通过超导实现的引力电耦合》（"Gravitoelectric-electric coupling via superconductivity"）。《物理学基础通讯》（Foundations of Physics Letters）。6（4）：371–383。Bibcode:1993FoPhL...6..371T。doi:10.1007/BF00665654。S2CID 122075917。
258. Kowitt (1994)。
259. Harris, Edward G. (1999)。《对道格拉斯·G·托尔和宁·李"通过超导实现的引力电耦合"的评论》（"Comments on 'Gravitoelectric-Electric Coupling via Superconductivity' by Douglas G. Torr and Ning Li"）。《物理学基础通讯》（Foundations of Physics Letters）。12（2）：201–208。doi:10.1023/A:1021621425670。S2CID 115204136。
260. Woods (2005)。
261. Tajmar, Martin 和 de Matos, Clovis (2006)。《旋转超导体中的引力磁场解决库珀对质量异常问题》（"Gravitomagnetic Fields in Rotating Superconductors to Solve Tate's Cooper Pair Mass Anomaly"）（PDF）。AIP 会议论文集（AIP Conf. Proc.）813：1415–1420。arXiv:gr-qc/0607086。Bibcode:2006AIPC..813.1415T。doi:10.1063/1.2169327。S2CID 24997124。
262. Li, N.; Noever, D.; Robertson, T.; Koczor, R.; Brantley, W. (1997 年 8 月)。《II 型 YBCO 超导体引力耦合静态测试》（"Static Test for a Gravitational Force Coupled to Type II YBCO Superconductors"）。《物理学 C》（Physica C）。281（2–3）：260–267。Bibcode:1997PhyC..281..260L。doi:10.1016/S0921-4534(97)01462-7。
263. Lucentini (2000)。
264. 《根据 10 USC 2371 在 2001 财年签署的合作协议和其他交易年度报告》（"Annual Report on Cooperative Agreements and Other Transactions Entered into During FY2001 Under 10 USC 2371"）。美国国防部（DOD）。第 66 页。存档于 2021 年 8 月 1 日，检索于 2014 年 3 月 6 日。
265. Cook (2002)。
266. Froning, H. 和 Roach, R. (2002)。《通过流体动力学近似模拟量子真空与飞行器的相互作用》（"Preliminary Simulations of Vehicle Interactions with the Quantum Vacuum by Fluid Dynamic Approximations"）。AIAA 第 38 届联合推进会议论文集。第 52236 页。doi:10.2514/6.2002-3925。ISBN 978-1-62410-115-1。
267. Fontana, Giorgio 和 Binder, Bernd (2009 年 3 月 16 日)。《通过核全论实现电磁波向引力波的转换》（"Electromagnetic to Gravitational wave Conversion via Nuclear Holonomy"）。AIP 会议论文集（AIP Conference Proceedings）。1103（1）：524–531。Bibcode:2009AIPC.1103..524F。doi:10.1063/1.3115561。ISSN 0094-243X。
268. Pauling, Linus (1965 年 10 月)。《原子核的紧密堆积-球模型及其与壳模型的关系》（"The Close-Packed-Spheron Model of Atomic Nuclei and ITS Relation to the Shell Model"）。《美国国家科学院院刊》（Proceedings of the National Academy of Sciences）。54（4）：989–994。Bibcode:1965PNAS...54..989P。doi:10.1073/pnas.54.4.989。ISSN 0027-8424。PMC 219778。PMID 16578621。
269. White, March, Williams 等 (2011)。
270. Maxey, Kyle (2012 年 12 月 11 日)。《星际规模推进——量子真空等离子体推进器》（"Propulsion on an Interstellar Scale – the Quantum Vacuum Plasma Thruster"）。engineering.com。检索于 2016 年 10 月 24 日。
271. Hambling, David(2014 年 7 月 31 日)。《NASA 验证 “不可思议” 的太空驱动》（"Nasa validates 'impossible' space drive"）。《Wired UK》。检索于 2016 年 10 月 24 日。
272. White, March, Lawrence 等 (2016)。
273. Drake, Nadia 和 Greshko, Michael (2016 年 11 月 21 日)。《NASA 团队声称 “不可思议” 的太空引擎有效——事实真相》（"NASA Team Claims 'Impossible' Space Engine Works—Get the Facts"）。《国家地理》（National Geographic）。存档于 2016 年 11 月 22 日，检索于 2016 年 11 月 22 日。

媒体文章

• Battersby, S. (2008 年 11 月 20 日)。“确认：物质只是真空波动”。发表于 New Scientist。存档于 2017 年 5 月 27 日。
• Bennett, J. (2016 年 11 月 30 日)。“科学家捕捉到‘虚粒子’出现和消失的现象”。发表于 Popular Mechanics。存档于 2017 年 5 月 29 日。
• Cho, A. (2015 年 10 月 1 日)。“物理学家观察到空旷空间中的奇怪量子波动——或许”。发表于 Science。doi:10.1126/science.aad4655。存档于 2017 年 5 月 27 日。
• Cho, A. (2016 年 11 月 30 日)。“天文学家发现空间中奇怪量子扭曲的迹象”。发表于 Science。doi:10.1126/science.aal0437。存档于 2017 年 5 月 29 日。
• Choi, C. Q. (2013 年 2 月 12 日)。“从无中生有？真空可以产生闪光”。发表于 Scientific American。存档于 2017 年 5 月 30 日。
• Chown, M. (1990 年 4 月 7 日)。“科学：光子可以‘超光速’传播吗？”。发表于 New Scientist。存档于 2017 年 5 月 30 日。
• Cook, N. (2002 年 7 月 29 日)。“反重力推进公开化”。发表于 Jane's Defence Weekly，伦敦。存档于 2002 年 8 月 2 日。
• Crane, L. (2016 年 11 月 30 日)。“量子粒子被观察到扭曲中子星发出的光”。发表于 New Scientist。存档于 2017 年 5 月 29 日。
• Davies, P. C. W. (1994 年 9 月 22 日)。“惯性理论：神奇的圆环——Paul Davies 论马赫原理的意义”。发表于 The Guardian。存档于 1999 年 1 月 17 日。
• Davies, P. C. W. (2011 年 11 月 19 日)。“以太之外：真空的变化面貌”。发表于 *New Scientist，第 212 卷，第 2839 期，第 50–52 页。Bibcode:2011NewSc.212Q..50D。doi:10.1016/S0262-4079(11)62858-3。
• Lucentini, J. (2000 年 9 月 28 日)。“重量问题：NASA 资助争议性的引力屏蔽研究”。发表于 SPACE.com。存档于 2000 年 11 月 9 日。
• Matthews, R. (1995 年 2 月 25 日)。“像真空一样无物”。发表于 New Scientist，第 145 卷，第 1966 期，第 30–33 页。存档于 2016 年 4 月 13 日。通过 Calphysics Institute 获取。
• O'Carroll, E. (2013 年 3 月 25 日)。“科学家研究‘无’，却发现了‘有’”。发表于 Christian Science Monitor。存档于 2013 年 3 月 31 日。
• Pilkington, M. (2003 年 7 月 17 日)。“零点能”。发表于 The Guardian。存档于 2017 年 2 月 7 日。
• Powell, C. S. (1994 年)。“无法承受的轻：一种新理论或许解释了为何物体倾向于保持静止”。发表于 Scientific American。第 270 卷，第 5 期，第 30–31 页。doi:10.1038/scientificamerican0594-27。
• Scott, W. B. (2004 年 3 月)。“奔向星辰”（PDF）。发表于 Aviation Week & Space Technology，第 50–53 页。存档于 2017 年 2 月 26 日，检索于 2016 年 10 月 25 日。
• Siegel, E. (2016 年 9 月 22 日)。“‘无’的物理是什么？”。发表于 Forbes。存档于 2017 年 5 月 27 日。
• Shiga, D. (2005 年 9 月 28 日)。“真空能：从无中得有？”。发表于 New Scientist。存档于 2017 年 5 月 27 日。
• Wall, M. (2014 年 3 月 27 日)。“暗能量来源于‘量子真空’？”。发表于 SPACE.com。存档于 2014 年 3 月 29 日。

参考文献

• Abbott, D.; Davis, B. R.; Phillips, N. J.; Eshraghian, K.(1996)。“使用窗口限制傅里叶变换和其他难题的热噪声公式的简单推导”。发表于 IEEE Transactions on Education，39 (1): 1–13。Bibcode:1996ITEdu..39....1A。CiteSeerX: 10.1.1.129.5792。doi:10.1109/13.485226。
• Barton, G.; Scharnhorst, K. (1993)。“平行镜间的量子电动力学：比光速快或被真空放大的光信号”。发表于 Journal of Physics A: Mathematical and General，26 (8): 2037–2046。Bibcode:1993JPhA...26.2037B。doi:10.1088/0305-4470/26/8/024。
• Battersby, Stephen (2016)。“暗能量：凝视黑暗”。发表于 *Nature*，537 (7622): 201–204。Bibcode:2016Natur.537S.201B。doi:10.1038/537S201a。PMID: 27681049。S2CID: 4398296。
• Bordag, M.; Klimchitskaya, G. L.; Mohideen, U.; Mostepanenko, V. M. (2009)。Advances in the Casimir Effect*。牛津：牛津大学出版社。ISBN: 978-0-19-923874-3。LCCN: 2009279136。OCLC: 319209483。
• Bostick, W. H.; Prior, W.; Grunberger, L.; Emmert, G. (1966)。“等离子体涡旋的对生成”。发表于 Physics of Fluids，9 (10): 2078。Bibcode:1966PhFl....9.2078B。doi:10.1063/1.1761572。
• Bressi, G.; Carugno, G.; Onofrio, R.; Ruoso, G. (2002)。“平行金属表面间 Casimir 力的测量”。发表于 *Physical Review Letters，88 (4): 041804。arXiv:quant-ph/0203002。Bibcode:2002PhRvL..88d1804B。doi:10.1103/PhysRevLett.88.041804。PMID: 11801108。S2CID: 43354557。
• Capasso, F.; Munday, J. N.; Iannuzzi, D.; Chan, H. B. (2007)。“Casimir 力和量子电动力学扭矩：物理学与纳米机械”* (PDF)。发表于 IEEE Journal of Selected Topics in Quantum Electronics*，13 (2): 400–414。Bibcode:2007IJSTQ..13..400C。doi:10.1109/JSTQE.2007.893082。S2CID: 32996610。
• Carroll, S. M.; Field, G. B. (1997)。“遥远射电源极化中的宇宙各向异性的证据？” (PDF)。发表于 Physical Review Letters，79 (13): 2394–2397。arXiv:astro-ph/9704263。Bibcode:1997PhRvL..79.2394C。doi:10.1103/PhysRevLett.79.2394。ISSN: 0031-9007。S2CID: 13943605。
• Chan, H. B.; Aksyuk, V. A.; Kleiman, R. N.; Bishop, D. J.; Capasso, F. (2001)。“通过 Casimir 力对微电机械系统的量子机械驱动” (PDF)。发表于 Science，291 (5510): 1941–1944。Bibcode:2001Sci...291.1941C。doi:10.1126/science.1057984。PMID: 11239149。S2CID: 17072357。
• Conlon, T. E. (2011). *Thinking About Nothing: Otto Von Guericke and The Magdeburg Experiments on the Vacuum*。旧金山：圣奥斯汀出版社。ISBN: 978-1-4478-3916-3。OCLC: 840927124。
• Correa, L. A.; Palao, J. P.; Alonso, D.; Adesso, G. (2014). “量子增强吸收制冷机”。发表于 Scientific Reports，4 (3949): 3949。arXiv:1308.4174。Bibcode:2014NatSR...4E3949C。doi:10.1038/srep03949。PMC: 3912482。PMID: 24492860。
• Davies, P. C. W. (1985). Superforce: The Search for a Grand Unified Theory of Nature。纽约：Simon and Schuster。ISBN: 978-0-671-47685-4。LCCN: 84005473。OCLC: 12397205。
• Decca, R. S.; López, D.; Fischbach, E.; Krause, D. E. (2003). “异质金属之间的 Casimir 力测量”。发表于 Physical Review Letters，91 (5): 050402。arXiv:quant-ph/0306136。Bibcode:2003PhRvL..91e0402D。doi:10.1103/PhysRevLett.91.050402。PMID: 12906584。S2CID: 20243276。
• Dirac, Paul A. M. (1927). “辐射发射与吸收的量子理论”* (PDF)。发表于 Proc. R. Soc. A，114 (767): 243–265。Bibcode:1927RSPSA.114..243D。doi:10.1098/rspa.1927.0039。存档于 2016 年 10 月 25 日，检索于 2016 年 10 月 17 日。
• Drexhage, K. H. (1970). “单分子层与光”。发表于 Scientific American，222 (3): 108–119。Bibcode:1970SciAm.222c.108D。doi:10.1038/scientificamerican0370-108。
• Drexhage, K. H.(1974). “IV 光与单分子染料层的相互作用”。收录于 Wolf, E. (编)。Progress in Optics，第 12 卷，页 163–232。doi:10.1016/S0079-6638(08)70266-X。ISBN: 978-0-444-10571-4。
• Dunne, G. V. (2012). “海森堡-欧拉有效作用：75 周年”。发表于 International Journal of Modern Physics A*，27 (15): 1260004。arXiv:1202.1557。Bibcode:2012IJMPA..2760004D。doi:10.1142/S0217751X12600044。ISSN: 0217-751X。S2CID: 119258601。
• Einstein, A. (1995). Klein, Martin J.; Kox, A. J.; Renn, Jürgen; Schulmann, Robert (编)。The Collected Papers of Albert Einstein Vol. 4 The Swiss Years: Writings, 1912–1914*。普林斯顿：普林斯顿大学出版社。ISBN: 978-0-691-03705-9。OCLC: 929349643。
• Einstein, A. (1993). Klein, Martin J.; Kox, A. J.; Schulmann, Robert (编)。The Collected Papers of Albert Einstein Vol. 5 The Swiss Years: Correspondence, 1902–1914。普林斯顿：普林斯顿大学出版社。ISBN: 978-0-691-03322-8。OCLC: 921496342。
• Goy, P.; Raimond, J. M.; Gross, M.; Haroche, S. (1983). “腔增强单原子自发发射的观察”。发表于 Physical Review Letters，50 (24): 1903–1906。Bibcode:1983PhRvL..50.1903G。doi:10.1103/PhysRevLett.50.1903。
• Greiner, W.; Müller, B.; Rafelski, J. (2012). Quantum Electrodynamics of Strong Fields: With an Introduction into Modern Relativistic Quantum Mechanics。Springer 出版社。doi:10.1007/978-3-642-82272-8。ISBN: 978-0-387-13404-8。LCCN: 84026824。OCLC: 317097176。
• Haisch, B.; Rueda, A.; Puthoff, H. E. (1994). “惯性作为零点场洛伦兹力” (PDF)。发表于 *Physical Review A，49 (2): 678–694。Bibcode:1994PhRvA..49..678H。doi:10.1103/PhysRevA.49.678。PMID: 9910287。存档于 2018 年 7 月 31 日，检索于 2016 年 10 月 17 日。
• Heisenberg, W.; Euler, H. (1936). “Dirac 正电子理论的推论”。发表于 Zeitschrift für Physik*，98 (11–12): 714–732。arXiv:physics/0605038。Bibcode:1936ZPhy...98..714H。doi:10.1007/BF01343663。ISSN: 1434-6001。S2CID: 120354480。
• Heyl, J. S.; Shaviv, N. J. (2000). “强磁场中的偏振演化”。发表于 Monthly Notices of the Royal Astronomical Society*，311 (3): 555–564。arXiv:astro-ph/9909339。Bibcode:2000MNRAS.311..555H。doi:10.1046/j.1365-8711.2000.03076.x。ISSN: 0035-8711。S2CID: 11717019。
• Itzykson, C.; Zuber, J.-B. (1980). *Quantum Field Theory* (2005 版)。纽约：Dover Publications。ISBN: 978-0486445687。LCCN: 2005053026。OCLC: 61200849。
• Kostelecký, V. Alan; Mewes, M. (2009). “具有任意维洛伦兹违反算子的电动力学”。发表于 *Physical Review D，80 (1): 015020。arXiv:0905.0031。Bibcode:2009PhRvD..80a5020K。doi:10.1103/PhysRevD.80.015020。ISSN: 1550-7998。S2CID: 119241509。
• Kostelecký, V. Alan; Mewes, M. (2013). “来自伽马射线暴的相对论违反约束”。发表于 *Physical Review Letters，110 (20): 201601。arXiv:1301.5367。Bibcode:2013PhRvL.110t1601K。doi:10.1103/PhysRevLett.110.201601。ISSN: 0031-9007。PMID: 25167393。S2CID: 8579347。
• Kowitt, Mark. (1994). “超导体中的引力磁效应与磁导率”。发表于 Physical Review B，49 (1): 704–708。Bibcode:1994PhRvB..49..704K。doi:10.1103/PhysRevB.49.704。PMID: 10009347。
• Kragh, H. (2002). Quantum Generations: A History of Physics in the Twentieth Century。普林斯顿大学出版社。ISBN: 978-0-691-09552-3。OCLC: 248763258。
• Kragh, H. (2012). “暗能量的前奏：零点能与真空推测”。发表于 *Archive for History of Exact Sciences*，66 (3): 199–240。arXiv:1111.4623。doi:10.1007/s00407-011-0092-3。ISSN: 0003-9519。S2CID: 118593162。
• Kragh, H. S.; Overduin, J. M. (2014). The Weight of the Vacuum: A Scientific History of Dark Energy。纽约：Springer 出版社。ISBN: 978-3-642-55089-8。LCCN: 2014938218。OCLC: 884863929。
• Kuhn, T. (1978). Black-Body Theory and the Quantum Discontinuity, 1894–1912。纽约：牛津大学出版社。ISBN: 978-0-19-502383-1。LCCN: 77019022。OCLC: 803538583。
• Le Bellac, M. (2006). Quantum Physics (2012 版)。剑桥大学出版社。ISBN: 978-1-107-60276-2。OCLC: 957316740。
• Leuchs, G.; Sánchez-Soto, L. L. (2013). “带电基本粒子的求和规则”。发表于 The European Physical Journal D，67 (3): 57。arXiv:1301.3923。Bibcode:2013EPJD...67...57L。doi:10.1140/epjd/e2013-30577-8。ISSN: 1434-6060。S2CID: 118643015。
• Loudon, R. (2000). 《光的量子理论》（第三版）。牛津：牛津大学出版社。ISBN: 978-0198501770。LCCN: 2001265846。OCLC: 44602993。
• Matthews, R. (1994). “惯性：空旷的空间是否提供阻力？” 发表在 Science，263 (5147): 612–613。Bibcode:1994Sci...263..612M。doi:10.1126/science.263.5147.612。ISSN: 0036-8075。JSTOR: 2883066。PMID: 17747645 – 经由 Calphysics Institute。
• Mignani, R. P.; Testa, V.; González Caniulef, D.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. (2017). “通过对孤立中子星 RX J1856.5−3754 的首个光学偏振测量发现真空双折射的证据” (PDF)。发表于 *Monthly Notices of the Royal Astronomical Society*，465 (1): 492–500。arXiv:1610.08323。Bibcode:2017MNRAS.465..492M。doi:10.1093/mnras/stw2798。ISSN: 0035-8711。S2CID: 38736536。
• Milonni, P. W. (1981). “辐射反应与电子的非相对论理论”。发表于 Physics Letters A，82 (5): 225–226。Bibcode:1981PhLA...82..225M。doi:10.1016/0375-9601(81)90191-2。
• Milonni, P. W. (1983). “电子的电磁质量是否取决于它的位置？” 发表在 International Journal of Theoretical Physics*，22 (4): 323–328。Bibcode:1983IJTP...22..323M。doi:10.1007/BF02082897。S2CID: 119991060。
• Milonni, P. W. (1994). 《量子真空：量子电动力学导论》。波士顿：Academic Press。ISBN: 978-0124980808。LCCN: 93029780。OCLC: 422797902。
• Milonni, P. W. (2009). “零点能”*。收录于 *Greenberger, D.; Hentschel, K.; Weinert, F.* (编辑)，《量子物理百科：概念、实验、历史与哲学》。柏林、海德堡：Springer 出版社，第 864–866 页。arXiv:0811.2516。doi:10.1007/978-3-540-70626-7。ISBN: 9783540706229。LCCN: 2008942038。OCLC: 297803628。
• Peebles, P. J. E.; Ratra, Bharat. (2003). “宇宙学常数与暗能量”。发表于 Reviews of Modern Physics，75 (2): 559–606。arXiv:astro-ph/0207347。Bibcode:2003RvMP...75..559P。doi:10.1103/RevModPhys.75.559。ISSN: 0034-6861。S2CID: 118961123。
• Penrose, Roger. (2004). 《通向现实之路》（第八版）。纽约：Alfred A. Knopf 出版社。ISBN: 978-0-679-45443-4。OCLC: 474890537。
• Perlmutter, S.; Aldering; Goldhaber; Knop; Nugent; Castro; Deustua; Fabbro; Goobar 等 (1999). “从 42 颗高红移超新星中测量Ω和Λ”。发表于 Astrophysical Journal，517 (2): 565–586。arXiv:astro-ph/9812133。Bibcode:1999ApJ...517..565P。doi:10.1086/307221。S2CID: 118910636。
• Peskin, M. E.; Schroeder, D. V. (1995). 《量子场论导论》。Addison-Wesley 出版社。ISBN: 978-0-201-50397-5。OCLC: 635667163。
• Pinto, F. (1999). *“一种光控真空能量转换器的引擎循环”。发表于 *Physical Review B，60 (21): 14740。Bibcode:1999PhRvB..6014740P。doi:10.1103/PhysRevB.60.14740。
• Planck, M.(1900). “关于能量分布定律的理论”。发表于 Verhandlungen der Deutschen Physikalischen Gesellschaft，2: 237–245。
• Planck, M. (1911). “一种新的辐射假设”。发表于 Verhandlungen der Deutschen Physikalischen Gesellschaft，13: 138–148。
• Planck, M. (1912a). “黑体辐射定律的基础”。发表于 Annalen der Physik，37 (4): 642–656。Bibcode:1912AnP...342..642P。doi:10.1002/andp.19123420403。
• Planck, M. (1912b). “黑体辐射定律与基本作用量的假设”。收录于 Langevin, P.; Solvay, E.; de Broglie, M. (编辑)，《辐射与量子的理论》。巴黎：Gauthier-Villars 出版社，第 93–114 页。LCCN: unk84021539。OCLC: 5894537227。
• Planck, M. (1913). 《热辐射理论讲义》。莱比锡：J. A. Barth 出版社。OCLC: 924400975。
• Planck, M. (1958). 《物理学论文与演讲》（第二卷）。布伦瑞克：Vieweg & Sohn。LCCN: 59047616。OCLC: 603096370。
• Power, E. A. (1964). 《初级量子电动力学》。伦敦：Longmans。LCCN: 65020006。OCLC: 490279969。
• Reed, D. (1995). “基础电动力学与贝尔特拉米矢量场”。收录于 Barrett, Terence William; Grimes, Dale M.（编），《高级电磁学：基础、理论与应用》。新加坡：World Scientific，第 217–249 页。ISBN: 978-981-02-2095-2。
• Rees, Martin（编）(2012). 《宇宙》。纽约：DK 出版社。ISBN: 978-0-7566-9841-6。LCCN: 2011277855。OCLC: 851193468。
• Riek, C.; Seletskiy, D. V.; Moskalenko, A. S.; Schmidt, J. F.; Krauspe, P.; Eckart, S.; Eggert, S.; Burkard, G.; Leitenstorfer, A. (2015). “电场真空波动的直接采样” (PDF)。发表于 Science，350 (6259): 420–423。Bibcode:2015Sci...350..420R。doi:10.1126/science.aac9788。ISSN: 0036-8075。PMID: 26429882。S2CID: 40368170。
• Riess, A. G.; Filippenko; Challis; Clocchiatti; Diercks; Garnavich; Gilliland; Hogan; Jha; 等 (1998). “通过超新星的观测证据支持加速膨胀宇宙和宇宙学常数”。发表于 Astronomical Journal，116 (3): 1009–1038。arXiv:astro-ph/9805201。Bibcode:1998AJ....116.1009R。doi:10.1086/300499。S2CID: 15640044。
• Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. (2014). “超越卡诺极限的纳米级热机”。发表于 Physical Review Letters，112 (3): 030602。arXiv:1308.5935。Bibcode:2014PhRvL.112c0602R。doi:10.1103/PhysRevLett.112.030602。PMID: 24484127。S2CID: 1826585。
• Rugh, S. E.; Zinkernagel, H. (2002). “量子真空与宇宙学常数问题”。发表于 Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics，33 (4): 663–705。arXiv:hep-th/0012253。Bibcode:2002SHPMP..33..663R。doi:10.1016/S1355-2198(02)00033-3。ISSN: 1355-2198。S2CID: 9007190。
• Saunders, Simon; Brown, Harvey R.（编）(1991). 《真空的哲学》。牛津：牛津大学出版社。ISBN: 978-0198244493。LCCN: 90048906。OCLC: 774073198。
• Schwinger, J. (1998a). 《粒子、源与场：第一卷》。雷丁，马萨诸塞州：Advanced Book Program, Perseus Books。ISBN: 978-0-7382-0053-8。LCCN: 98087896。OCLC: 40544377。
• Schwinger, J. (1998b). 《粒子、源与场：第二卷》。雷丁，马萨诸塞州：Advanced Book Program, Perseus Books。ISBN: 978-0-7382-0054-5。LCCN: 98087896。OCLC: 40544377。
• Schwinger, J. (1998c). 《粒子、源与场：第三卷》。雷丁，马萨诸塞州：Advanced Book Program, Perseus Books。ISBN: 978-0-7382-0055-2。LCCN: 98087896。OCLC: 40544377。
• Sciama, D. W. (1991). “量子场的真空状态的物理意义”。收录于 Saunders, Simon; Brown, Harvey R.（编），《真空的哲学》。牛津：牛津大学出版社。ISBN: 978-0198244493。LCCN: 90048906。OCLC: 774073198。
• Scott, Alwyn (2006). 《非线性科学百科全书》。Routledge 出版社。ISBN: 978-1-57958-385-9。OCLC: 937249213。
• Scully, M. O.; Zubairy, M. S. (1997). 《量子光学》。英国剑桥：剑桥大学出版社。ISBN: 978-0-521-43595-6。OCLC: 444869786。
• Scully, M. O. (2001). “通过量子负熵从单一热浴中提取能量”。发表于 *Physical Review Letters*，87 (22): 220601。Bibcode:2001PhRvL..87v0601S。doi:10.1103/PhysRevLett.87.220601。PMID: 11736390。
• Scully, M. O.; Zubairy, M. S.; Agarwal, G. S.; Walther, H. (2003). “通过消失的量子相干性从单一热浴中提取能量”。发表于 *Science，299 (5608): 862–863。Bibcode:2003Sci...299..862S。doi:10.1126/science.1078955。PMID: 12511655。S2CID: 120884236。
• Urban, M.; Couchot, F.; Sarazin, X.; Djannati-Atai, A. (2013). “量子真空作为光速的起源”。发表于 The European Physical Journal D，67 (3): 58。arXiv:1302.6165。Bibcode:2013EPJD...67...58U。doi:10.1140/epjd/e2013-30578-7。ISSN: 1434-6060。S2CID: 15753833。
• Weinberg, S. (1989). “宇宙学常数问题”(PDF)。发表于 Reviews of Modern Physics，61 (1): 1–23。Bibcode:1989RvMP...61....1W。doi:10.1103/RevModPhys.61.1。hdl:2152/61094。ISSN: 0034-6861。S2CID: 122259372。
• Weinberg, S. (2015). 《量子力学讲义》（第二版）。剑桥：剑桥大学出版社。ISBN: 978-1-107-11166-0。LCCN: 2015021123。OCLC: 910664598。
• Weisskopf, V. (1936). “基于电子量子理论的真空电动力学” (PDF)。发表于 Kongelige Danske Videnskabernes Selskab, Mathematisk-fysiske Meddelelse，24 (6): 3–39。
• White, H.; March, P.; Lawrence, J.; Vera, J.; Sylvester, A.; Brady, D.; Bailey, P. (2016). “真空中封闭射频腔的脉冲推力测量”。发表于 Journal of Propulsion and Power*，33 (4): 830–841。doi:10.2514/1.B36120。hdl:2060/20170000277。S2CID: 126303009。
• White, H.; March, P.; Williams, N.; O'Neill, W. (2011 年 12 月 5 日)。“Eagleworks 实验室：先进推进物理研究” (PDF)。在 JANNAF 联合推进会议 上发表；时间：2011 年 12 月 5–9 日；地点：阿拉巴马州亨茨维尔。检索日期：2016 年 10 月 24 日。
• Wilson, C. M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J. R.; Duty, T.; Nori, F.; Delsing, P. (2011). “在超导电路中观察到的动态卡西米尔效应”。发表于 Nature，479 (7373): 376–379。arXiv:1105.4714。Bibcode:2011Natur.479..376W。doi:10.1038/nature10561。ISSN: 0028-0836。PMID: 22094697。S2CID: 219735。
• Woods, R. C. (2005). “利用超导体操控引力波进行通信应用”。发表于 Physica C: Superconductivity*，433 (1–2): 101–107。Bibcode:2005PhyC..433..101W。doi:10.1016/j.physc.2005.10.003。
• Woods, R. C.; Cooke, S. G.; Helme, J.; Caldwell, C. H. (2001). “通过高温超导体修改重力”。发表于 AIAA 第 37 届联合推进会议与展览。doi:10.2514/6.2001-3363。

15. 进一步阅读

新闻文章

• Brumfiel, G. (2011 年 6 月 3 日). “移动的镜子从无中创造光”。发表于 *Nature*。doi:10.1038/news.2011.346。
• Brooks, M. (2011 年 11 月 16 日). “从空旷空间中提取光”。发表于 New Scientist。存档于 2017 年 5 月 30 日。
• Cartlidge, E. (2011 年 11 月 17 日). “如何将黑暗转化为光”*。发表于 Physics World，物理学会出版。存档于 2017 年 5 月 30 日。
• Marcus, A. (2009 年 10 月 12 日). “在真空中研究：DARPA 尝试利用难以捉摸的 Casimir 效应开发突破性技术”*。发表于 Scientific American*。存档于 2015 年 3 月 2 日。
• Matthews, R.; Sample, I. (1996 年 9 月 1 日). “‘反重力’设备让科学迈进”。发表于 The Sunday Telegraph。存档于 2003 年 3 月 6 日。
• Sciama, D. W. (1978 年 2 月 2 日). “以太的蜕变”。发表于 New Scientist，第 77 卷，第 1088 期，第 298-300 页。通过 Google Books 检索。
• Yirka, B. (2015 年 10 月 2 日). “研究团队声称直接采样了电场真空涨落”。发表于 Phys.org。存档于 2017 年 5 月 27 日。

期刊文章

• Boyer, T. H. (1970). “量子零点能量与长距离力”。发表于 Annals of Physics*，56 (2): 474–503。Bibcode:1970AnPhy..56..474B。doi:10.1016/0003-4916(70)90027-8。ISSN: 0003-4916。
• Bulsara, A. R.; Gammaitoni, L. (1996). “调谐噪声” (PDF)。发表于 Physics Today，49 (3): 39–45。Bibcode:1996PhT....49c..39B。doi:10.1063/1.881491。ISSN: 0031-9228。存档于 2018 年 7 月 12 日。检索日期：2017 年 5 月 31 日。
• Lahteenmaki, P.; Paraoanu, G. S.; Hassel, J.; Hakonen, P. J. (2013). “约瑟夫森超材料中的动态 Casimir 效应”。发表于 Proceedings of the National Academy of Sciences，110 (11): 4234–4238。arXiv:1111.5608。Bibcode:2013PNAS..110.4234L。doi:10.1073/pnas.1212705110。ISSN: 0027-8424。S2CID: 10972781。

书籍

• Beiser, A. (2003). 《现代物理概念》（第 6 版）。波士顿：麦格劳-希尔。ISBN: 978-0072448481。LCCN: 2001044743。OCLC: 48965418。
• Heitler, W. (1984). 《辐射的量子理论》（1954 年再版，第 3 版）。纽约：Dover 出版社。ISBN: 978-0486645582。LCCN: 83005201。OCLC: 924845769。
• Rafelski, J.; Muller, B. (1985). 《结构化的真空：思考无》 (PDF)。Thun: H. Deutsch。ISBN: 978-3871448898。LCCN: 86175968。OCLC: 946050522。

16. 外部链接

• 尼玛·阿卡尼-哈梅德（Nima Arkani-Hamed）谈真空能量和暗能量问题。
• 史蒂文·温伯格（Steven Weinberg）论宇宙学常数问题。