控制理论(综述)
贡献者: addis
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
控制系统工程中的控制理论是数学的一个子领域,用于控制工程过程和机器中连续运行的动力系统。其目的是开发一种控制模型,用于以最佳方式使用控制动作来控制这些系统,而没有延迟或过冲并确保控制的稳定性。
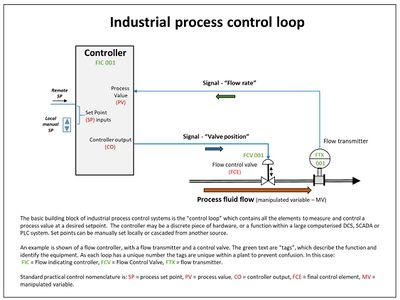
为此,需要具有纠正措施的 控制器。该控制器监控受控过程变量(PV),并将其与参考点或设定点进行比较。过程变量的实际值和期望值之差,称为误差信号或 SP-PV 误差,作为反馈,产生控制动作,使受控过程变量达到与设定值相同的值。值得研究的其他方面还包括可控性和可观察性。在此基础上,先进的自动化技术彻底改变了制造业、飞机、通信和其他行业。反馈控制,通常是连续的,包括使用传感器进行测量并进行计算调整,以通过 “最终控制元件”(例如控制阀)将测量变量保持在设定范围内。[1]
广泛使用的通常是被称为框图的图解样式。其中传递函数也被称为系统函数或网络函数,是描述系统的微分方程的输入和输出之间关系的数学模型。
控制理论的起源可以追溯到 19 世纪,当时詹姆斯·克拉克·麦克斯韦首次描述了调速器运行的理论基础。[2]1874 年,爱德华·劳斯,查尔斯·斯特姆及随后的 1895 年,阿道夫·胡尔维茨进一步完善了控制理论,他们都对控制稳定性标准的建立做出了贡献;从 1922 年起,尼古拉斯·米诺斯基发展了 PID 控制理论。[3]虽然控制理论的一个主要应用是控制系统工程,它涉及工业过程控制系统的设计,但其应用远远不止这些。作为反馈系统的一般理论,控制理论对于存在反馈的任何地方都是有用的。
1. 历史
虽然各种类型的控制系统可以追溯到古代,但对该领域更正式的分析始于物理学家詹姆斯·克拉克·麦克斯韦在 1868 年进行的对离心调速器的动力学分析,题名为 On Governors。[4]离心调速器已经被用来调节风车的速度。[5]麦克斯韦描述和分析了自振荡现象,其中系统的滞后可能会导致过度补偿和不稳定行为。这种现象引起了人们的兴趣,在此期间,麦克斯韦的同学爱德华·约翰·劳斯抽象了麦克斯韦对于一般线性系统的描述。[6]阿道夫·胡尔维茨在 1877 年使用微分方程独立分析了系统的稳定性,从而产生了现在的 “劳斯–赫尔维茨定理”。[7][8]
动态控制的一个显著应用是在载人飞行领域。莱特兄弟于 1903 年 12 月 17 日的首次成功试飞,并以其长时间控制飞行的能力而闻名(从机翼产生升力的能力)。对于持续几秒钟以上的飞行需要对飞机进行持续、可靠的控制。
第二次世界大战后,控制理论正成为一个重要的研究领域。Irmgard Flügge-Lotz 发展了不连续自动控制系统的理论,并将 bang-bang 原理应用于飞机自动飞行控制设备的开发。[9][10]不连续控制的其他应用领域包括火控系统、制导系统和电子设备。
有时,机械方法被用来提高系统的稳定性。例如,船舶稳定器是安装在吃水线下并横向伸出的鳍。在当代船只中,它们可以是陀螺控制的有源鳍,这些鳍有能力改变它们的迎角,以抵消作用在船只上的风或波浪引起的滚转。
太空竞赛也依赖于精确的航天器控制,此外,控制理论在经济学等领域也得到越来越多的应用。
2. 开环和闭环(反馈)控制
本质上讲,有两种类型的控制回路:开环控制和闭环(反馈)控制。
在开环控制中,控制器的控制动作独立于 “过程输出”(或 “受控过程变量”- PV)。这方面的一个很好的例子是中央供暖锅炉,它仅由计时器控制,因此无论建筑物的温度如何,热量都持续施加。控制动作是锅炉的定时开/关,过程变量是建筑温度,但两者不相关。
在闭环控制中,控制器的控制动作取决于以过程变量值形式的过程反馈。在锅炉模拟的情况下,闭环将包括恒温器,以比较建筑物温度(PV)和恒温器上设置的温度(设置点- SP)。这产生了控制器输出,通过打开和关闭锅炉来将建筑物保持在期望的温度。因此,闭环控制器具有反馈回路,该反馈回路确保控制器施加控制动作以做操过程变量,使其与 “参考输入” 或 “设定点” 相同。因此,闭环控制器也被称为反馈控制器。[11]
根据英国标准协会,闭环控制系统的定义是 “具有监控反馈的控制系统,由该反馈形成的偏差信号被用于控制最终控制元件的动作,以偏差减小到零为目的。”[12]
同样地;“反馈控制系统 是一种倾向于通过比较这些变量的功能并使用差异作为控制手段来维持一个系统变量与另一个系统变量的规定关系的系统。"[13]
2.1 其他例子
控制系统的一个例子是汽车的巡航控制,这是一种设计用于将车辆速度维持在由驾驶员提供的恒定期望或参考速度的装置。控制器巡航控制,平台是汽车,系统包括是汽车和巡航控制系统。系统输出是汽车的速度,控制本身是发动机的油门位置,它决定了发动机提供的功率。
实现巡航控制的一种简单方法是当驾驶员使用巡航控制时,锁定油门位置。然而,如果巡航控制系统在一段平坦的道路上运行,那么汽车上坡时会行驶得很慢,下坡时会行驶得更快。这种没有反馈的控制器称为开环控制器;没有测量系统输出(汽车的速度)来改变控制(油门位置)。因此,控制器不能补偿在汽车上的变化,例如道路坡度的变化。
在闭环控制系统 中,来自监控汽车速度(系统输出)的传感器的数据进入控制器,控制器持续比较代表速度的量和代表期望速度的参考量。这种差异称为误差,决定了油门位置(控制)。目的是使汽车速度与参考速度相匹配(保持所需的系统输出)。当汽车上坡时,输入(检测到的速度)和参考值之间的差值决定油门位置。当检测到的速度下降到参考值以下时,差值增加,油门打开,发动机功率增加,从而加速车辆。这样,控制器动态地抵消汽车速度的变化。这些控制系统的中心思想是反馈回路,控制器影响系统输出,系统输出又被测量并反馈给控制器。
3. 经典控制理论
为了克服开环控制器的局限性,控制理论引入了反馈。闭环控制器使用反馈来控制动力系统的状态或输出。其名称来自系统中的信息路径: 过程输入(例如,施加到电动机的电压)对过程输出(例如,电动机的速度或扭矩)有影响,过程输出由传感器测量并由控制器处理;结果(控制信号)作为输入 “反馈” 到过程中,结束循环。
闭环控制器相比于开环控制器具有以下优点:
- 干扰抑制(例如上面巡航控制示例中的山丘)
- 当模型结构与实际过程不完全匹配且模型参数不准确时,即使存在模型不确定性,也能保证性能
- 将易变的过程趋于稳定
- 对参数变化的敏感度降低
- 改进的参考跟踪性能
在一些系统中,闭环和开环控制同时使用。在这样的系统中,开环控制被称为前馈,用于进一步改善参考跟踪性能。
常见的闭环控制器架构是 PID 控制器。
4. 闭回路传递函数
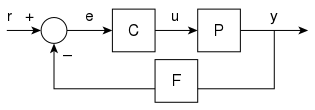
系统的输出 $y(t)$ 通过传感器测量将 F 反馈并与参考值 $r(t)$ 进行比较。获取参考和输出之间的误差 $e$(差值)以改变输入 $u$ 控制下的系统 $P$。系统框图如下所示。这种控制器被称为闭环控制器或反馈控制器。
也被称为单输入单输出 $(SISO)$ 控制系统;系统具有多个输入/输出被称为 $MIMO$(即多输入多输出)系统。在这种情况下,变量通过向量表示,而不是简单的标量值。对于一些分布式参数系统,向量可以是无限维的(通常是函数)。
假设存在控制器 $C$,平台 $P$,和线性时不变传感器 $F$ (即,传递函数中的元素包括不依赖于时间的 $C(s)$,$P(s)$,和 $F(s))$,上述系统可以对变量进行拉普拉斯变换来分析。给出了以下关系:
$Y(s)=P(s)U(s)$
$U(s)=C(s)E(s)$
$E(s)=R(s)-F(s)Y(s)$
利用 $r(s )$ 求解 $Y(s) )$:
表达式 $H(s) = \frac{P(s)C(s)}{1 + F(s)P(s)C(s)}$ 被称为闭环系统的传递函数。分子是 $r$ 到 $y$ 的正向(开环)增益,分母是 1 加上环绕反馈环路的增益,即所谓的环路增益。如果 $\left| P(s)C(s) \right| \gg 1$ 即,它具有大值的范数,值为 $s$),如果 $\left| F(s) \right| \approx 1$,则 $Y(s)$ 大约等于 $R(s)$ 并且输出会紧密跟踪参考输入。
5. PID 反馈控制
比例 - 积分 - 微分控制器(PID 控制器)是一个广泛应用于控制系统的控制回路反馈机构控制技术。
PID 控制器连续计算期望的设定点和测量的过程变量之间的误差值 $e(t$),并基于比例、积分和导数项进行校正。PID 是 Proportional-Integral-Derivative 的首字母缩写,指的是对误差信号进行操作以产生控制信号的三个术语。
理论理解和应用可以追溯到 20 世纪 20 年代,它们几乎在所有模拟控制系统中得到实施;最初用于机械控制器,随后应用于离散电子设备,如今大量应用于工业过程计算机。PID 控制器可能是最常用的反馈控制设计。
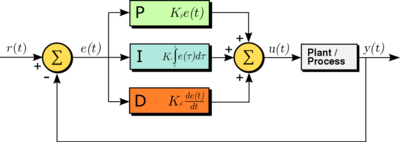
如果 $u(t)$ 是发送给系统的控制信号,$y(t)$ 是测量的输出,$r(t)$ 是期望的输出,并且跟踪误差值 $e(t) = r(t) - y(t)$,则 PID 控制器的一般形式可以表示为:
$u(t) = K_P e(t) + K_I \int e(\tau) d\tau + K_D \frac{d e(t)}{dt}.$
通过调整三个参数获得所需的闭环动态特性 $K_P$、$K_I$ 和 $K_D$,通常通过 “调试” 反复进行,并且不需要特定的平台模型。稳定性通常可以只用比例项来保证。积分项可以抑制阶跃干扰(通常是过程控制中引人注目的现象)。导数项用于提供响应的阻尼或整形。PID 控制器是最成熟的一类控制系统;然而,它们不适用于一些复杂的情况,特别是对于 MIMO 系统。
应用拉普拉斯变换得到变换后的 PID 控制器方程为:
$u(s) = K_P e(s) + K_I \frac{1}{s} e(s) + K_D s e(s)$
$u(s) = \left(K_P + \frac{K_I}{s} + K_D s \right) e(s)$
PID 控制器的传递函数为:
$C(s) = \left( K_P + K_I \frac{1}{s} + K_D s \right)$
作为闭环系统 $H(s)$ 中 PID 控制器调试的一个例子,对于一级响应,则有:
$P(s) = \frac{A}{1 + sT_P}$
其中 $A$ 和 $T_P$ 是常数。响应的输出通过下式给出:
$F(s) = \frac{1}{1 + sT_F}$
其中,$T_F$ 也是一个常数。如何设置有 $K_P = K \left( 1 + \frac{T_D}{T_I} \right)$, $K_D = K T_D$, 和 $K_I =\frac{K}{T_I}$,则 PID 控制器的传递函数可以用级数表示为:
$C(s) = K \left( 1 + \frac{1}{s T_I} \right) (1 + s T_D)$
将 $P(s)$, $F(s)$ 和 $C(s)$ 带入闭环传递函数 $H(s)$,则会发现通过设置下列参数,
将得到 $H(s) = 1$。通过本例中的调试,系统输出将完全遵循参考输入值。
然而,在实践中,由于系统中噪声和谐振模式的放大,纯微分器物理上不可实现的,也不是理想的[14]。因此,需要使用相位超前补偿器或具有低通滚降的微分器来代替。
6. 线性和非线性控制理论
控制理论领域可以分为两个分支:
- 线性控制理论——适用于由遵循叠加原理的设备组成的系统,输出与输入成正比。它们由线性微分方程控制。一个主要的子类是具有不随时间变化参数的系统,称为线性时不变系统(LTI)系统。这些系统适用于强大的频域数学技术,如拉普拉斯变换、傅立叶变换、Z 变换、波特图、根轨迹和奈奎斯特稳定判据。需要使用诸如带宽、频率响应、特征值、增益、谐振频率、零点和极点等术语来描述系统,这些描述术语为大多数感兴趣的系统提供了系统响应和设计技术的解决方案。
- 非线性控制理论——因为所有的实际控制系统都是非线性的,因此非线性理论可以应用在更真实的系统中。这些系统通常由非线性微分方程控制,开发用于处理它们的少数数学技术更加困难且不那么通用,通常仅适用于狭窄的系统类别。其中包括极限环理论,Poincaré映射,李亚普诺夫稳定性定理,和描述函数。非线性系统的分析通常使用计算机上的数值计算方法,例如通过使用仿真语言对系统进行模拟。如果只关心稳定点附近的解,那么非线性系统通常可以通过使用扰动理论的线性系统对其进行近似线性化,并且可以使用线性技术。[15]
7. 分析技术-频域和时域
分析和设计控制系统的数学技术分为两类:
- 频域——在此类型中,状态变量的值表示系统的输入、输出以及用频率表示反馈函数。输入信号和系统的转移函数由时间函数转换为频率函数,例如采用傅里叶变换,拉普拉斯变换,或 Z 变换。这项技术的优点是它简化了数学计算;表示系统的微分方程 由更简单的频域代数方程 替代。然而,如上所述频域技术只能用于线性系统。
- 时域状态空间表示——在此类型中,状态变量的值表示为时间的函数。使用该模型,被分析的系统由一个或多个微分方程组成,因为频域技术限于线性系统,因此时域技术被广泛用于分析现实世界的非线性系统。虽然时域计算更加困难,但现代计算机模拟技术(如模拟语言)已使其分析成为常规。 与经典控制理论的频域分析相反,现代控制理论使用时域状态空间表示,这是一个物理系统的数学模型,作为由一阶微分方程相关的输入、输出和状态变量的集合。为了从输入、输出和状态的数量中抽象出来,变量被表示为向量,微分方程和代数方程被写成矩阵的形式(后者仅在动力系统是线性的时才可能实现)。状态空间表示方法(也称为 “时域方法”)提供了一种方便而紧凑的方法来建模和分析具有多个输入和输出的系统。有了输入和输出,我们将不得不进行拉普拉斯变换来编码关于系统的所有信息。与频域方法不同,状态空间表达式的使用不限于具有线性分量和零初始条件的系统。“状态空间” 是指其轴是状态变量的空间。系统的状态可以表示为该空间中的一个点。[16][17]
8. 系统接口- SISO 和 MIMO
根据输入和输出的数量,控制系统可以分为不同的类别。
- 单输入单输出(SISO)——这是最简单和最常见的类型,其中一个输出由一个控制信号控制。例如上面的巡航控制示例或者音频控制系统,其中控制输入的是输入音频信号,输出是来自扬声器的声波。
- 多输入多输出(MIMO)——这些在更复杂的系统中可以找到。例如,现代大型望远镜例如 Keck 和 MMT 具有由许多单独段组成的镜子,每个段由其独立的激励器进行激励。整个镜子的形状由 MIMO 主动光学控制系统不断调整,使用来自焦平面上的多个传感器的输入,以补偿由于热膨胀,收缩,旋转时的应力和扭曲引起的镜子形状的变化,以及大气中的湍流对波前的影响。诸如核反应堆和人体细胞的复杂系统均可由计算机模拟为大型的 MIMO 控制系统。
9. 控制理论中的主题
9.1 稳定性
稳定性 在没有输入的一般动力系统中可以用李亚普诺夫稳定性判据来描述。
- 如果一个线性系统的输出对于任何有界输入都保持有界,则被称为是有界输入有界输出(BIBO)稳定的系统。
- 采用输入的非线性系统的稳定性是输入到状态的稳定性(ISS),它结合了李亚普诺夫稳定性和类似于 BIBO 稳定性的概念。
为简单起见,以下描述主要集中在连续时间和离散时间线性系统。
数学上,这意味着因果线性系统要稳定,其传递函数的所有极点必须具有负实值,即每个极点的实部必须小于零。实际上,稳定性要求传递函数存在复数极点。
- 当用拉普拉斯变换获得传递函数时,极点位于连续时间复平面的左半部分。
- 当使用 Z 变换时,极点位于在离散时间的单位圆内。
这两种情况之间的差异仅仅是由于绘制连续时间与离散时间传递函数的方法不同。连续拉普拉斯变换在笛卡尔坐标系中 x 轴是实轴,离散 Z 变换在圆坐标中,其中 $\rho $ 轴是真正的轴。
当满足上述适当条件时,系统被称为是渐近稳定的;渐近稳定控制系统的变数总是从其初始值开始减少,并且不会有永久的振荡。当极点的实部恰好等于 0(在连续时间情况下)或模数等于 1(在离散时间情况下)时,就会发生永久振荡。如果简单稳定的系统响应既不随时间衰减也不随时间增长,并且没有振荡,则它是临界稳定的;在这种情况下,系统传递函数在复平面原点处有不重复的极点(即在连续时间下,它们的实部和虚部为零)。当实部等于零的极点虚部不等于零时,就会出现振荡。
如果所讨论的系统的冲激响应为
$x[n] = 0.5^n u[n]$
Z 变换(见这个例子)由下式给出:
$X(z) = \frac{1}{1 - 0.5z^{-1}}$
存在一个 $z = 0.5$(零虚数)的极点。这个系统是 BIBO(渐近)稳定的,因为极点位于单位圆中。
然而,如果冲激响应为:
$x[n] = 1.5^n u[n]$
那么 Z 变换就是:
$ X(z) = \frac{1}{1 - 1.5z^{-1}} $
它的极点在 $z = 1.5$ 处,由于极点的模值大于 1,因此是 BIBO 不稳定的。
有许多工具可以用来分析系统的极点。包括图形系统,如根轨迹、波特图或奈奎斯特图。
机械变化可以使设备(和控制系统)更加稳定。水手们增加压舱物来提高船只的稳定性。游轮使用从船侧横向延伸大约 30 英尺(10 米)的防侧倾鳍,并围绕其轴线连续旋转以产生与侧倾相反的力,从而防止侧翻。
9.2 可控性和可观察性
在确定要应用的最佳控制策略之前,可控性和可观察性是系统分析中的主要问题,或者描述为系统是否可以控制或稳定。可控性与通过使用适当的控制信号迫使系统进入特定状态的可能性相关。如果一个状态是不可控的,那么就没有信号能够控制这个状态。如果一个状态是不可控的,但它的动力学是稳定的,那么这个状态被称为可稳定的。相反,观察性与通过输出测量观察系统状态的可能性有关。如果状态是不可观察的,控制器将永远无法确定不可观察状态的行为,因此不能使用它来稳定系统。然而,类似于上面的可稳定条件,如果不能观察到状态,则它可能是可检测的。
从几何角度来看,观察待控制系统中每个变量的状态,这些变量的每个 “坏” 状态都必须是可控的和可观察的,以确保闭环系统中的良好行为。也就是说,如果系统的一个特征值不可控制和观察,则这部分动力学将在闭环系统中保持不变。如果这样的特征值不稳定,则该特征值的动力学将出现在闭环系统中,因此闭环系统将是不稳定的。在状态空间表达式的传递函数实现中不存在不可观测的极点,这就是为什么在动力系统分析中有时优选后者。
不可控或不可观察系统问题的解决方案包括添加执行器和传感器。
9.3 控制规格
在过去的几年中已经存在有几种不同的控制策略。这些控制器从非常通用的( PID 控制器)到专门用于非常特殊类别系统的其他控制器(机器人或飞机巡航控制)。
控制问题可以有几种规格。当然,稳定总是存在的。无论开环稳定性如何,控制器必须确保闭环系统稳定。控制器选择不当甚至会降低开环系统的稳定性,这通常是必须避免的。有时希望在闭环中获得特定的动力学:即极点具有 $ \operatorname{Re} [\lambda] < -\overline{\lambda}$,其中 $\overline{\lambda}$ 是一个严格大于零的固定值,而不是简单地令 $ \operatorname{Re} [\lambda] < 0$。
另一个典型规格是抑制阶跃干扰;在开环链中添加积分器(即直接在受控系统之前)很容易实现这一点。而其他类型的扰动需要包括不同类型的子系统。
其他 “经典” 控制理论规范涉及闭环系统的时间响应。这些参数包括上升时间(控制系统在扰动后达到期望值所需的时间)、峰值过冲(响应在达到期望值之前达到的最高值)以及其他参数(建立时间,四分之一衰减)。频域规格通常与鲁棒性相关(见下文)。
如今,通常使用集成跟踪误差的一些变量(IAE,ISA,CQI)来评估系统性能。
9.4 模型识别和鲁棒性
控制系统必须始终具有一定的鲁棒性。鲁棒控制:如果应用于与其合成所用的数学系统略有不同的系统,则其特性不会有太大变化。这一要求很重要,因为没有一个真正的物理系统能够完全与表示它的数学微分方程一样。通常选择更简单的数学模型来简化计算,否则,真正的系统动力学可能会非常复杂,以至于不可能有完整的模型。
系统辨识
确定控制模型动力学方程的过程称为系统识别。这一步骤可以离线完成:例如,执行一系列测量,从中计算近似数学模型,通常是其传递函数或矩阵。然而,这种从输出中的识别不能考虑不可观察的动态。有时模型是直接从已知的物理方程建立的,例如,在我们知道的质量-弹簧-阻尼器系统可以由式 $m\ddot{x}(t) = -Kx(t) - B\dot{x}(t)$ 进行描述。即使假设在设计控制器时使用了 “完整” 的模型,这些方程中包含的所有参数(称为 “标称参数”)也永远不会具有绝对精度;即使连接到真实参数值与标称值不同的物理系统,控制系统也必须正确运行。
一些先进的控制技术包括 “在线” 识别过程(见下文)。当控制器本身运行时,计算(“识别”)模型的参数。这样,如果参数发生剧烈变化,例如,如果机器人的手臂释放了重量,控制器将进行自我调整以确保正确的性能。
分析
考虑到系统的传递函数,并使用奈奎斯特图和波特图,可以在频域中分析 SISO(单输入单输出)控制系统的鲁棒性。包括增益和相位裕度以及幅度裕度。对于 MIMO(多输入多输出)和一般更复杂的控制系统,必须考虑为每种控制技术设计的理论结果(见下一节)。也就是说,如果需要特定的鲁棒性,工程师需将其注意力转移到控制技术上,以将它们包含在控制技术的属性中。
限制
特定的鲁棒性问题是要求控制系统在存在输入和状态约束的情况下正确执行。在现实世界中,每个信号都是有限的。控制器可能会发送物理系统无法跟踪的控制信号,例如,试图以过高的速度旋转阀门。这可能会导致闭环系统出现不良行为,甚至损坏执行器或其他子系统。可以使用特定的控制技术来解决这个问题:模型预测控制(见下文)和防缠绕系统。后者包括一个附加的控制块,确保控制信号永远不会超过给定的阈值。
10. 系统分类
10.1 线性系统控制
对于多输入多输出系统,极点配置可以使用开环系统的状态空间表示进行数学计算,并计算在所需位置分配极点的反馈矩阵。在复杂的系统中,这可能需要计算机辅助计算能力,并且不能一直确保鲁棒性。此外,并非所有系统状态都是一般测量的,因此观测器必须包含在极点配置设计中。
10.2 非线性系统控制
像机器人和航空航天工业等行业的过程通常具有很强的非线性动力学。在控制理论中,有时可以应用线性技术线性化这类系统,但在许多情况下,有必要从头设计允许控制非线性系统的理论。例如,反馈线性化,反推,滑模控制,轨迹线性化控制通常利用基于李亚普诺夫理论的结果。微分几何(Differential geometry)已被广泛用作将众所周知的线性控制概念推广到非线性情形的工具,并显示出使其成为解决更具挑战性问题的微妙之处。控制理论也被用来破译指导认知状态的神经机制。[18]
10.3 分散系统控制
当系统由多个控制器控制时,则存在分散控制问题。权力下放在许多方面都有帮助,例如,它有助于控制系统在更大的地理区域内运行。分散控制系统中的代理可以使用通信信道进行交互,并协调它们的动作。
10.4 确定性和随机系统控制
随机控制问题是状态变量的演化受到系统外部随机冲击的影响。确定性控制问题不受外部随机冲击的影响。
11. 主要控制策略
每个控制系统首先必须保证闭环行为的稳定性。对于线性系统,这可以通过直接放置极点来获得。非线性控制系统使用特定的理论(通常基于亚历山大·李亚普诺夫理论)来确保稳定性,而不考虑系统的内部动态。满足不同规格的可能性因所考虑的模型和所选择的控制策略而异。
主要控制技术列表
- 自适应控制使用过程参数的在线识别或对控制器增益的修改,从而获得强鲁棒性。自适应控制在 20 世纪 50 年代首次应用于航空航天工业,并在该领域取得了特别的成功。
- 分级控制系统是一种控制系统,其中一组设备和控制软件以分级树方式排列。当树中的链路由计算机网络实现时,该分级控制系统也是网络控制系统的一种形式。
- 智能控制使用各种人工智能计算方法,如人工神经网络,贝叶斯概率,模糊逻辑,[19] 机器学习、进化计算和遗传算法来控制动态系统。
- 最优控制是一种特殊的控制技术,其中控制信号优化某个 “成本指数”:例如,在卫星上,喷射推力需要将它带到消耗最少燃料的期望轨迹。两种最优控制设计方法在工业应用中得到了广泛应用,因为它们可以保证闭环稳定性,包括模型预测控制和线性二次高斯控制 (LQG)。第一种方法可以更明确地考虑系统中信号的约束,这是许多工业过程中的一个重要特征。然而,模型预测控制中的 “最佳控制” 结构只是达到此目的的一种手段,因为它不能优化闭环控制系统的真实性能指标。MPC 系统与 PID 控制器一起是过程控制中应用最广泛的控制技术。
- 鲁棒控制明确处理控制器设计方法中的不确定性。控制器设计使用鲁棒控制方法往往能够处理真实系统和设计使用的名义模型之间的微小差异。[20]Bode 和其他人的早期方法相当稳健;20 世纪 60 年代和 70 年代发明的状态空间方法有时被发现缺乏鲁棒性。现代鲁棒控制技术的例子包括由邓肯·麦克法拉尼和基思·格洛弗开发的 H-infinity 环路整形,瓦迪姆·乌特金开发的滑模控制,以及用于控制智能电网应用中大型异构电负载群的安全协议。[21]鲁棒方法旨在对存在小建模误差的情况下实现鲁棒性能或稳定性。
- 随机控制涉及模型中具有不确定性的控制设计。在典型的随机控制问题中,假设模型和控制器中存在随机噪声和干扰,控制设计必须考虑这些随机偏差。
- 能量整形控制将工厂和控制器视为能量转换设备。控制策略是根据互连的方式(以保持功率的方式)制定的,以便实现期望的行为。
- 自组织临界控制可以定义为试图干扰自组织系统耗散能量的过程。
12. 系统和控制的相关人物
许多活跃的历史人物对控制理论做出了重要贡献,包括
- 皮埃尔·西蒙·拉普拉斯在他概率论的工作中发明了 Z 变换,现在用于解决离散时间控制理论问题。Z 变换是以他的名字拉普拉斯变换命名的离散时间等价物。
- Irmgard Flugge-Lotz 发展了间断自动控制理论,并将其应用于自动飞机控制系统。
- 亚历山大·李亚普诺夫于 19 世纪 90 年代开创了稳定性理论。
- 哈罗德·布莱克在 1927 年发明了负反馈放大器的概念。20 世纪 30 年代,他开发出稳定的负反馈放大器。
- 哈利·奈奎斯特在 20 世纪 30 年代为反馈系统开发了奈奎斯特稳定判据。
- 理查德·贝尔曼从 20 世纪 40 年代开始了动态规划的开发。[22]
- 安德雷·柯尔莫哥洛夫在 1941 年共同开发了维纳-科尔莫戈罗夫滤波器。
- 诺伯特·维纳在 20 世纪 40 年代共同开发了维纳-科尔莫戈罗夫滤波器,并创造了术语控制论。
- 约翰·拉加兹尼在 20 世纪 50 年代在控制理论中引入了数字控制和 Z 变换(由拉普拉斯发明)。
- 列夫·庞特里亚金介绍了最大值原理和爆炸原理。
- 皮埃尔-路易·利翁将粘度解发展成随机控制和最优控制方法。
- 鲁道夫·卡尔曼开创了系统和控制的状态空间法。引入了可控性和可观性的概念。开发了用于线性估计的卡尔曼滤波器。
- Ali H. Nayfeh 是非线性控制理论的主要贡献者之一,出版了许多关于微扰理论的书籍
- Jan C. Willems 引入了耗散性概念,将李亚普诺夫函数推广到对输入/状态/输出系统。作为李雅普诺夫函数的类比,存储函数的构造促进了控制理论中线性矩阵不等式(LMI)的研究。他开创了数学系统理论的行为方法。
13. 参考文献
[1] ^斯图尔特·班尼特(1992)。控制工程史,1930-1955。IET。第 48 页。ISBN 978-0-86341-299-8。.
[2] ^Maxwell, J. C. (1868). "On Governors" (PDF). Proceedings of the Royal Society. 100..
[3] ^Minorsky, Nicolas (1922). "Directional stability of automatically steered bodies". Journal of the American Society of Naval Engineers. 34 (2): 280–309. doi:10.1111/j.1559-3584.1922.tb04958.x..
[4] ^Maxwell, J.C. (1868). "On Governors". Proceedings of the Royal Society of London. 16: 270–283. doi:10.1098/rspl.1867.0055. JSTOR 112510..
[5] ^控制理论:历史、数学成就和前景|·费尔南德斯·卡拉 1 和埃·祖阿祖阿.
[6] ^Routh, E.J.; Fuller, A.T. (1975). Stability of motion. Taylor & Francis..
[7] ^Routh, E.J. (1877). A Treatise on the Stability of a Given State of Motion, Particularly Steady Motion: Particularly Steady Motion. Macmillan and co..
[8] ^Hurwitz, A. (1964). "On The Conditions Under Which An Equation Has Only Roots With Negative Real Parts". Selected Papers on Mathematical Trends in Control Theory..
[9] ^Flugge-Lotz, Irmgard; Titus, Harold A. (October 1962). "Optimum and Quasi-Optimum Control of Third and Fourth-Order Systems" (PDF). Stanford University Technical Report (134): 8–12..
[10] ^Hallion, Richard P. (1980). Sicherman, Barbara; Green, Carol Hurd; Kantrov, Ilene; Walker, Harriette, eds. Notable American Women: The Modern Period: A Biographical Dictionary. Cambridge, Mass.: Belknap Press of Harvard University Press. pp. 241–242. ISBN 9781849722704..
[11] ^“反馈和控制系统”——JJ·迪·斯泰法诺,阿尔·斯图布拉德,IJ·威廉姆斯。夏姆斯轮廓系列,麦格劳-希尔 1967.
[12] ^Mayr, Otto (1970). The Origins of Feedback Control. Clinton, MA USA: The Colonial Press, Inc..
[13] ^Mayr, Otto (1969). The Origins of Feedback Control. Clinton, MA USA: The Colonial Press, Inc..
[14] ^Ang, K.H.; Chong, G.C.Y.; Li, Y. (2005). "PID control system analysis, design, and technology". IEEE Transactions on Control Systems Technology. 13 (4): 559–576. doi:10.1109/TCST.2005.847331..
[15] ^修剪点.
[16] ^Donald M Wiberg. State space & linear systems. Schaum's outline series. McGraw Hill. ISBN 978-0-07-070096-3..
[17] ^Terrell, William (1999). "Some fundamental control theory I: Controllability, observability, and duality —AND— Some fundamental control Theory II: Feedback linearization of single input nonlinear systems". American Mathematical Monthly. 106 (9): 705–719 and 812–828. doi:10.2307/2589614. JSTOR 2589614..
[18] ^Gu Shi; et al. (2015). "Controllability of structural brain networks (Article Number 8414)". Nature Communications. 6 (6). arXiv:1406.5197. Bibcode:2015NatCo...6E8414G. doi:10.1038/ncomms9414. Lay summary. Here we use tools from control and network theories to offer a mechanistic explanation for how the brain moves between cognitive states drawn from the network organization of white matter microstructure..
[19] ^Liu, Jie; Wilson Wang; Farid Golnaraghi; Eric Kubica (2010). "A novel fuzzy framework for nonlinear system control". Fuzzy Sets and Systems. 161 (21): 2746–2759. doi:10.1016/j.fss.2010.04.009..
[20] ^Melby, Paul; et., al. (2002). "Robustness of Adaptation in Controlled Self-Adjusting Chaotic Systems". Fluctuation and Noise Letters. 02 (4): L285–L292. doi:10.1142/S0219477502000919..
[21] ^N. A. Sinitsyn. S. Kundu, S. Backhaus (2013). "Safe Protocols for Generating Power Pulses with Heterogeneous Populations of Thermostatically Controlled Loads". Energy Conversion and Management. 67: 297–308. arXiv:1211.0248. doi:10.1016/j.enconman.2012.11.021..
[22] ^Richard Bellman (1964). "Control Theory" (PDF). Scientific American. Vol. 211 no. 3. pp. 186–200..