卡西米尔效应（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：平行板上的卡西米尔力

　　 在量子场论中，卡西米尔效应（或称卡西米尔力）是一种作用在受限空间宏观边界上的物理力，它源于场的量子涨落。当该效应以单位面积上的力来描述时，有时会使用 “卡西米尔压力” 这一术语。[2][3] 这一效应以荷兰物理学家亨德里克·卡西米尔的名字命名，他于 1948 年预测了电磁系统中的这一效应。

　　 同年，卡西米尔与迪尔克·波尔德一起描述了一个类似的效应，这一效应发生在中性原子靠近宏观界面时，称为卡西米尔–波尔德力。[4] 他们的结果是对伦敦–范德瓦尔斯力的推广，且包括了由于光速有限所导致的时滞。伦敦–范德瓦尔斯力、卡西米尔力和卡西米尔–波尔德力的基本原理可以在同一框架下进行表述。[5][6]

　　 在 1997 年，史蒂文·K·拉莫罗进行了直接实验，定量测量了卡西米尔力，结果与理论预测值相差不超过 5%。[7]

　　 卡西米尔效应可以通过以下观点理解：宏观物质界面的存在，如电导体和介电体，改变了第二量子化电磁场能量的真空期望值。[8][9] 由于这一能量的值依赖于材料的形状和位置，卡西米尔效应表现为这些物体之间的力。

　　 任何支持振荡的介质都有类似的卡西米尔效应。例如，绳上的珠子[10][11]，以及浸入湍流水或气体中的板[12][13]都能说明卡西米尔力。

　　 在现代理论物理中，卡西米尔效应在质子的手征袋模型中起着重要作用；在应用物理中，它在一些新兴的微技术和纳米技术中具有重要意义。[14]

1. 物理性质

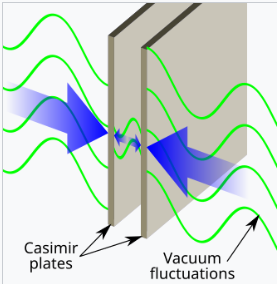
　　 典型的例子是两个未带电的导电板，在真空中相距几纳米。在经典描述中，缺乏外部场意味着板间不存在场，也没有力将它们连接在一起。[15] 但是，当使用量子电动力学真空来研究这个场时，可以看到板对构成场的虚拟光子产生影响，并产生一个净力[16]——这种力要么是吸引力，要么是排斥力，取决于板的具体排列。尽管卡西米尔效应可以通过虚拟粒子与物体的相互作用来表达，但最好通过量子化场在物体之间的零点能量来描述，并且更容易计算。这个力已经被测量，并且是一个由第二量子化正式捕捉到的效应的典型例子。[17][18]

　　 在这些计算中，边界条件的处理存在争议。事实上，“卡西米尔的原始目标是计算导电板上可极化分子之间的范德瓦尔斯力。” 因此，它可以在没有任何提及量子场的零点能量（真空能量）的情况下进行解释。[19]

　　 由于该力的强度随距离迅速减小，因此只有在物体之间的距离很小时才能测量到。这种力变得非常强大，以至于在亚微米尺度下，它成为未带电导体之间的主导力。实际上，在 10 纳米的间距下——约为原子典型尺寸的 100 倍——卡西米尔效应产生相当于约 1 大气压的压力（精确值依赖于表面几何形状和其他因素）。[17]

2. 历史

　　 荷兰物理学家亨德里克·卡西米尔和迪尔克·波尔德在 1947 年于飞利浦研究实验室提出了两种可极化原子之间以及这种原子与导电板之间存在一种力；这种特殊形式的力被称为卡西米尔–波尔德力。[4] 在与尼尔斯·玻尔的对话后，玻尔建议这与零点能量有关，卡西米尔单独提出了理论，预测了中性导电板之间的力，这一现象被称为卡西米尔效应。[20]

　　 该力的预测后来扩展到了有限导电性的金属和介电体，而后来的计算则考虑了更一般的几何形状。在 1997 年前的实验中，卡西米尔力被定性地观察到，并通过测量液态氦薄膜的厚度间接验证了预测的卡西米尔能量。最终，1997 年拉莫罗的直接实验定量测量了卡西米尔力，结果与理论预测值相差不超过 5%。[7] 随后的实验则达到了几百分点的精度。

3. 可能的原因

真空能量

　　 卡西米尔效应的原因可以通过量子场论来描述，量子场论指出，所有各种基本场（如电磁场）必须在空间中的每一个点上量子化。在简化的视角下，可以将物理学中的 “场” 想象成空间中充满了相互连接的振动球和弹簧，场的强度可以通过球从其静止位置的位移来可视化。该场中的振动会传播，并受到特定场的适当波动方程的控制。量子场论的二次量子化要求每个这样的球-弹簧组合都要量子化，即场的强度必须在空间中的每一点上量子化。在最基本的层面上，空间中的每个点的场是一个简单的谐振子，而它的量子化意味着每个点都有一个量子谐振子。场的激发对应于粒子物理学中的基本粒子。然而，即使是真空也具有极其复杂的结构，因此所有的量子场论计算必须参考这种真空模型。

　　 真空隐含地拥有粒子可能具有的所有属性：自旋[21]（对于光来说是极化）、能量等等。平均而言，这些属性大多相互抵消：从这个意义上来说，真空毕竟是 “空的”。一个重要的例外是真空能量，或者说真空的能量期望值。简单谐振子的量子化表明，这样的谐振子可能具有的最低能量或零点能量为： \[ E = \frac{1}{2} \hbar \omega ~\] 对空间中所有点的所有可能谐振子进行求和会得到一个无穷大的量。由于只有能量差是物理上可测量的（有一个显著的例外是引力，它超出了量子场论的范围），因此这个无穷大可以被视为数学上的一个特性，而不是物理上的特性。这个论点是重正化理论的基础。在这种方式处理无穷大量曾是量子场论学者普遍不安的原因之一，直到 1970 年代重正化群的出现，这是一种为尺度变换提供自然基础的数学形式化方法。

　　 当物理学的范围扩展到包括引力时，对这种形式上无穷大的量的解释依然存在问题。目前尚没有令人信服的解释说明为什么它不应该导致一个比观测到的宇宙常数大几个数量级的值。[22] 然而，由于我们还没有完全一致的量子引力理论，因此同样也没有令人信服的理由说明它应该导致我们所观测到的宇宙常数值。[23]

　　 对于费米子，卡西米尔效应可以理解为费米子算符（−1）F 的谱不对称性，在这种情况下它被称为 Witten 指数。

相对论性范德瓦尔斯力

　　 另一种观点是，麻省理工学院的 Robert Jaffe 在 2005 年的一篇论文中指出：“卡西米尔效应可以在不涉及零点能量的情况下进行公式化，卡西米尔力也可以计算出来。它们是带电粒子和电流之间的相对论性量子力。平行板之间的卡西米尔力（单位面积）随着细结构常数α趋近于零而消失，而标准结果（似乎与α无关）对应于α趋近于无穷大的极限。” 他还指出：“卡西米尔力只是金属板之间的（相对论性、滞后）范德瓦尔斯力。”[19] 卡西米尔和波尔德的原始论文使用了这种方法来推导卡西米尔-波尔德力。1978 年，Schwinger、DeRadd 和 Milton 发布了一种类似的推导，描述了平行板之间的卡西米尔效应。[24] 更近期的研究中，Nikolic 从量子电动力学的基本原理出发，证明了卡西米尔力并非源自电磁场的真空能量，[25] 并用简单的语言解释了卡西米尔力的基本微观起源为何来自范德瓦尔斯力。[26]

4. 效应

　　 卡西米尔的观察是，存在于金属或介电体等大体物体中的二次量子化电磁场，必须遵循与经典电磁场相同的边界条件。特别地，这影响了在导体或介电体存在下真空能量的计算。

　　 举个例子，考虑计算金属腔体内电磁场的真空期望值，例如雷达腔体或微波波导。在这种情况下，正确的方式是通过求解腔体中驻波的能量来找到场的零点能量。每一个可能的驻波对应一个能量；假设第 n 个驻波的能量为 En。腔体内电磁场的真空期望值为： \[ \langle E \rangle = \frac{1}{2} \sum_{n} E_n~ \] 其中求和遍历所有可能的 n 值，列举所有驻波。因子 \( \frac{1}{2} \) 是因为第 n 模式的零点能量是 \( \frac{1}{2} E_n \)，其中 En 是第 n 模式的能量增量（这个 \( \frac{1}{2} \) 与方程 \( E = \frac{1}{2} \hbar \omega \) 中的 \( \frac{1}{2} \) 相同）。以这种方式写出来的和显然是发散的，但它可以用来构造有限的表达式。

　　 具体来说，可以问零点能量如何依赖于腔体形状 s。每个能级 En 依赖于形状，因此应该写为 \( E_n(s) \)，而真空期望值则是 \( \langle E(s) \rangle \)。此时，有一个重要的观察：如果壁的形状 s 在点 p 处稍微改变（比如通过δs），则壁上的力等于真空能量的变化。即，力为： \[ F(p) = - \left. \frac{\delta \langle E(s) \rangle}{\delta s} \right|_p~ \] 在许多实际计算中，这个值是有限的。[27]

　　 板间的吸引力可以通过专注于一维情况来理解。假设一个可移动的导电板位于与两个相距较远的板（距离为 l）之间的距离 a 处。当 \( a \ll l \) 时，槽内宽度为 a 的状态受到严格约束，使得任何一个模式的能量 E 与下一个模式的能量之间有很大的间隔。与此不同，在大区域 l 内，存在着大量的状态（约 \( \frac{l}{a} \) 个），这些状态的能量在 \( E \) 和下一个模式之间均匀分布，换句话说，所有的能量都略大于 E。现在，若将 a 缩短一个量 da（da 为负值），则窄槽中的模式波长缩小，从而使得能量增加，比例为 \( -\frac{da}{a} \)；而所有位于大区域内的 \( \frac{l}{a} \) 个状态波长拉长，能量相应减少，比例为 \( -\frac{da}{l} \)（注意分母不同）。这两个效应几乎互相抵消，但净变化略为负值，因为大区域内所有的 \( \frac{l}{a} \) 个模式的能量略大于槽中的单一模式。因此，力是吸引性的：它倾向于使板间的距离变小，板子彼此靠近，穿越狭窄的槽。

5. 卡西米尔效应的推导（假设使用ζ-正则化）

　　 在卡西米尔的原始计算中，他考虑了两个导电金属板之间的空间，板间距离为 a。在这种情况下，驻波的计算特别简单，因为电场的横向分量和磁场的法向分量必须在导体表面消失。假设板平行于 xy 平面，驻波为： \[ \psi_n(x, y, z; t) = e^{-i\omega_n t} e^{i k_x x + i k_y y} \sin\left(k_n z\right) ~ \] 其中ψ表示电磁场的电分量，为了简便，忽略了极化和磁分量。在这里，\( k_x \) 和 \( k_y \) 是平行于板的方向上的波数， \[ k_n = \frac{n\pi}{a}~ \] 是垂直于板的波数。这里，n 是整数，源于要求ψ在金属板上消失。该波的频率为： \[ \omega_n = c \sqrt{{k_x}^2 + {k_y}^2 + \frac{n^2 \pi^2}{a^2}}~ \] 其中 c 是光速。真空能量是所有可能激发模式的总和。由于板的面积很大，我们可以通过在 k 空间中对两个维度进行积分来进行求和。假设周期性边界条件，得到： \[ \langle E \rangle = \frac{\hbar}{2} \cdot 2 \int \frac{A \, dk_x \, dk_y}{(2\pi)^2} \sum_{n=1}^{\infty} \omega_n~ \] 其中 A 是金属板的面积，并引入了一个因子 2 来表示波的两种可能极化。这种表达式显然是无穷大的，为了继续计算，方便引入一个调节因子（下文将详细讨论）。这个调节因子将使得表达式变为有限的，最终会去掉。经过ζ-正则化的每单位面积的能量表达式为： \[ \frac{\langle E(s)\rangle}{A} = \hbar \int \frac{dk_x \, dk_y}{(2\pi)^2} \sum_{n=1}^{\infty} \omega_n \left|\omega_n\right|^{-s}~ \] 最后，要求取极限 \(s \to 0\)。这里的 s 是一个复数，不要与之前讨论的形状 s 混淆。对于实数且大于 3 的 s，这个积分和求和是有限的。这个和在 \(s = 3\) 处有一个极点，但可以通过解析延拓到 \(s = 0\)，使得表达式变为有限。上述表达式简化为： \[ \frac{\langle E(s)\rangle}{A} = \frac{\hbar c^{1-s}}{4\pi^2} \sum_{n} \int_0^\infty 2\pi q \, dq \left| q^2 + \frac{\pi^2 n^2}{a^2} \right|^{\frac{1-s}{2}}~ \] 其中引入了极坐标 \(q^2 = k_x^2 + k_y^2\) 将双重积分转化为单重积分。前面的 \(q\) 是雅可比因子，\(2\pi\) 来自角度积分。如果 \(\text{Re}(s) > 3\)，则该积分收敛，结果为： \[ \frac{\langle E(s)\rangle}{A} = - \frac{\hbar c^{1-s} \pi^{2-s}}{2a^{3-s}} \frac{1}{3-s} \sum_{n} |n|^{3-s} = - \frac{\hbar c^{1-s} \pi^{2-s}}{2a^{3-s}(3-s)} \sum_{n} \frac{1}{|n|^{s-3}}.~ \] 在 \(s\) 接近 0 时，这个和是发散的，但如果假设大频率激发的阻尼对应于黎曼ζ函数的解析延拓至 \(s = 0\) 是在某种意义上物理上合理的，那么有： \[ \frac{\langle E\rangle}{A} = \lim_{s \to 0} \frac{\langle E(s)\rangle}{A} = -\frac{\hbar c \pi^2}{6a^3} \zeta(-3)~ \] 但是 \(\zeta(-3) = \frac{1}{120}\)，所以得到： \[ \frac{\langle E\rangle}{A} = -\frac{\hbar c \pi^2}{720 a^3}~ \] 解析延拓显然消除了一个加法性的正无穷，巧妙地精确地解释了板间缝隙外部的零点能量（上述未包括），但这种能量会随着板块在封闭系统内的运动而变化。对于理想化的、完美导电的板和它们之间有真空的情况，每单位面积上的 Casimir 力 \(\frac{F_c}{A}\) 为： \[ \frac{F_{\mathrm{c}}}{A} = -\frac{d}{da} \frac{\langle E \rangle}{A} = -\frac{\hbar c \pi^2}{240 a^4}~ \] 其中：

　　 该力是负值，表示力是吸引力：将两块板移动得更近，能量降低。出现 \(\hbar\) 显示了每单位面积上的 Casimir 力 \(\frac{F_c}{A}\) 非常小，并且力本质上来源于量子力学。

　　 通过对上述方程积分，可以计算将两块板分离到无穷远所需的能量： \[ U_E(a) = \int F(a) \, da = \int -\frac{\hbar c \pi^2}{240 a^4} \, da = \frac{\hbar c \pi^2 A}{720 a^3}~ \] 其中：

　　 在 Casimir 的原始推导中，[20] 一块可移动的导电板被放置在两块相距较远的板之一的短距离 \(a\) 处（距离为 \(L\)）。考虑板两侧的零点能量。与上述解析延拓假设不同，使用 Euler–Maclaurin 求和法和正则化函数（例如指数正则化）计算发散的和与积分，而不是像上述的 \(|\omega_n|^{-s}\) 这么异常的情况。[28]

更近期的理论

　　 Casimir 对理想化金属板的分析被 Evgeny Lifshitz 和他的学生推广到任意介电材料和实际金属板的情况。[5][29] 使用这种方法，可以通过计算边界材料的复介电函数，数值计算由于有限导电性导致的 Casimir 力的修正。Lifshitz 的理论对于两块金属板，在板间距离 \(a\) 远大于金属的表皮深度时，归结为 Casimir 理想化的 \(\frac{1}{a^4}\) 力定律；而对于较小的 \(a\)，则归结为伦敦色散力的 \(\frac{1}{a^3}\) 力定律（其系数称为 Hamaker 常数），在中间距离时，力的依赖性较为复杂，由材料的色散决定。[30]

　　 Lifshitz 的结果随后被推广到任意多层平面几何以及各向异性和磁性材料，但数十年来，对于非平面几何形状的 Casimir 力的计算仍然仅限于一些理想化的情况，能够得到解析解。[31] 例如，在实验中的球形–平面几何中，使用了一个近似（由 Derjaguin 提出），即假设球的半径 \(R\) 远大于间隔 \(a\)，在这种情况下，附近的表面几乎是平行的，因此可以采用平行板的结果来近似计算 \(\frac{R}{a^3}\) 力（忽略表皮深度和更高阶曲率效应）。[31][32] 然而，在 2010 年代，一些作者开发并展示了多种数值技术，许多技术借用了经典计算电磁学的方法，这些方法能够准确计算任意几何形状和材料的 Casimir 力，从简单的有限尺寸效应（如有限板的效应）到更复杂的现象（如图案化表面或不同形状物体引起的效应）。[31][33]

6. 测量

　　 最早的实验测试之一是由 Marcus Sparnaay 在 1958 年于荷兰埃因霍温的飞利浦公司进行的。这是一个精细且困难的实验，使用平行板进行，结果与 Casimir 理论没有矛盾[34][35]，但存在较大的实验误差。

　　 1997 年，Steve K. Lamoreaux（来自洛斯阿拉莫斯国家实验室）[7] 以及 Umar Mohideen 和 Anushree Roy（来自加利福尼亚大学河滨分校）[36] 更准确地测量了 Casimir 效应。实际上，实验中并没有使用两块平行板（因为需要非常精确的对准来确保它们平行），而是使用一块平板和另一块作为球体一部分的板，球体具有非常大的半径。

　　 2001 年，由 Giacomo Bressi、Gianni Carugno、Roberto Onofrio 和 Giuseppe Ruoso 组成的小组在意大利帕多瓦大学最终成功地使用微谐振器测量了平行板之间的 Casimir 力。[37] 这些实验的多种变体被 Klimchitskaya 在 2009 年的综述中总结。[38]

　　 2013 年，由香港科技大学、佛罗里达大学、哈佛大学、麻省理工学院和橡树岭国家实验室的科学家们组成的团队展示了一种紧凑的集成硅芯片，可以测量 Casimir 力。[39] 由电子束光刻定义的集成芯片无需额外对准，使其成为测量复杂几何形状之间 Casimir 力的理想平台。2017 年和 2021 年，同一小组在香港科技大学展示了基于该芯片平台的非单调 Casimir 力[40] 和与距离无关的 Casimir 力[41]。

7. 正则化

　　 为了能够在一般情况下进行计算，引入正则化器在求和中是很方便的。这是一个人为的工具，用于使求和变为有限的，从而可以更容易地操作，之后通过取极限去除正则化器。

　　 热核或指数正则化的求和是： \[ \langle E(t) \rangle = \frac{1}{2} \sum_{n} \hbar |\omega_n| \exp\left(-t |\omega_n|\right) ~ \] 其中，最后取极限 \( t \to 0^+ \)。求和的发散通常表现为： \[ \langle E(t) \rangle = \frac{C}{t^3} + \text{finite}~ \] 对于三维腔体。求和中的无限部分与体积常数 \( C \) 相关，这不依赖于腔体的形状。求和的有趣部分是有限部分，它依赖于形状。高斯正则化器： \[ \langle E(t) \rangle = \frac{1}{2} \sum_{n} \hbar |\omega_n| \exp\left(-t^2 |\omega_n|^2 \right)~ \] 由于其优越的收敛性质，更适合用于数值计算，但在理论计算中更难使用。也可以使用其他适当平滑的正则化器。ζ函数正则化器： \[ \langle E(s) \rangle = \frac{1}{2} \sum_{n} \hbar |\omega_n| |\omega_n|^{-s}~ \] 完全不适用于数值计算，但在理论计算中非常有用。特别地，发散表现为复数 \( s \) 平面上的极点，体积发散出现在 \( s = 4 \) 处。这个求和可以通过解析延拓穿越这个极点，以在 \( s = 0 \) 处获得有限部分。

　　 并不是每个腔体配置都必然导致有限部分（即没有极点在 \( s = 0 \) 处）或形状独立的无限部分。在这种情况下，应理解必须考虑额外的物理因素。特别地，在极高频率（超过等离子体频率）下，金属对光子（如 X 射线）变得透明，而电介质也表现出频率依赖的截止效应。这种频率依赖性起到了自然正则化的作用。在固态物理中有许多与 Casimir 效应数学上非常相似的体积效应，其中截止频率明确起作用，以保持表达式有限。（这些在 Landau 和 Lifshitz 的《连续介质理论》中有更详细的讨论。）

8. 一般性

　　 卡西米尔效应也可以通过量子场论的函数积分的数学机制来计算，尽管这些计算更加抽象，因此更难理解。此外，这些计算只能在最简单的几何形状下进行。然而，量子场论的形式化使得它清楚地表明，真空期望值的求和在某种意义上是对所谓 “虚粒子” 的求和。

　　 更有趣的是，理解到对驻波能量的求和应当形式上被理解为对哈密顿量特征值的求和。这使得原子和分子效应（如范德华力）能够作为卡西米尔效应的变种来理解。因此，考虑系统的哈密顿量作为物体排列的函数，例如原子在配置空间中的排列。零点能量随着配置变化的变化，可以理解为在物体之间产生力的原因。

　　 在质子壳模型中，卡西米尔能量起着重要作用，表明质子的质量与壳半径无关。此外，谱不对称性被解释为重子数的非零真空期望值，抵消了围绕质子的π介子场的拓扑绕数。

　　 “伪卡西米尔” 效应可以在液晶系统中找到，其中通过刚性墙壁锚定施加的边界条件引发了类似于导体板之间的力的长程力。[42]

9. 动态卡西米尔效应

　　 动态卡西米尔效应是指由加速运动的镜子产生粒子和能量的现象。这一反应在 20 世纪 70 年代通过某些量子力学方程的数值解被预测出来。[43] 2011 年 5 月，瑞典哥德堡的查尔姆斯理工大学的研究人员宣布探测到动态卡西米尔效应。在他们的实验中，微波光子在超导微波谐振腔中从真空中生成。这些研究人员使用了一个改进版的 SQUID（超导量子干涉装置），通过在时间上改变谐振腔的有效长度，模拟了以所需相对论速度运动的镜子。如果这一结果得到确认，将是首次实验验证动态卡西米尔效应。[44][45] 2013 年 3 月，《PNAS》科学期刊发表了一篇文章，描述了一项实验，该实验在约瑟夫森超材料中演示了动态卡西米尔效应。[46] 2019 年 7 月，另一篇文章公布了一项实验，提供了光学动态卡西米尔效应在色散振荡光纤中的证据。[47] 2020 年，弗兰克·威尔切克等人提出了解决与动态卡西米尔效应的运动镜子模型相关的信息丧失悖论的方法。[48] 在弯曲时空的量子场论框架内，动态卡西米尔效应（运动镜子效应）被用来帮助理解 “乌尔赫效应”。[49]

10. 排斥力

　　 卡西米尔效应很少会导致无电荷物体之间产生排斥力。叶夫根尼·利夫希茨（Evgeny Lifshitz）理论上证明，在某些情况下（最常见的是涉及液体的情况），排斥力确实可以产生。[50] 这一发现引发了对卡西米尔效应在悬浮装置开发中的应用的兴趣。Munday 等人进行了基于卡西米尔效应的排斥力的实验演示，利夫希茨所预测的排斥力被描述为 “量子悬浮”。[51] 其他科学家也建议使用增益介质来实现类似的悬浮效应，[52][53] 尽管这一方法存在争议，因为这些材料似乎违反了基本的因果关系约束和热力学平衡要求（克拉美尔–克罗尼格关系）。实际上，对于足够各向异性的电介质，卡西米尔排斥力和卡西米尔–波尔德排斥力可以发生；有关排斥力问题的综述见 Milton 等人。[54] 最近关于排斥卡西米尔力的一个重要发展是使用手性材料。斯德哥尔摩大学的姜庆东（Q.-D. Jiang）和麻省理工学院的诺贝尔奖得主弗兰克·威尔切克（Frank Wilczek）表明，手性 “润滑剂” 可以产生排斥性、增强和可调的卡西米尔相互作用。[55]

　　 蒂莫西·博耶（Timothy Boyer）在 1968 年发表的研究[56]中表明，具有球对称性的导体也会表现出这种排斥力，并且结果与半径无关。进一步的研究表明，通过精心选择的电介质材料也可以产生这种排斥力。[57]

11. 猜测性应用

　　 有研究提出，卡西米尔力在纳米技术中可能有应用，特别是在基于硅集成电路技术的微机电系统（MEMS）和纳米机电系统，以及所谓的卡西米尔振荡器中。[58][59]

　　 1995 年和 1998 年，Maclay 等人[60][61]首次提出了带有卡西米尔力的微机电系统模型。虽然这些模型没有将卡西米尔力用于实际工作，但论文引起了 MEMS 领域的广泛关注，因为它揭示了卡西米尔效应需要被视为未来 MEMS 设计中的关键因素。特别是，卡西米尔效应可能是导致 MEMS 粘滞失效（stiction failure）的关键原因。[62]

　　 2001 年，Capasso 等人展示了如何利用卡西米尔力控制 MEMS 设备的机械运动。研究人员将一个多晶硅板悬挂在一个扭杆上——这是一个直径仅几微米的水平旋转杆。当他们将一个金属化球体靠近该板时，两物体之间的吸引性卡西米尔力使该板旋转。他们还通过使板振荡来研究 MEMS 设备的动态行为。卡西米尔力降低了振荡速率，并导致了非线性现象，例如振荡器频率响应中的滞后和双稳态现象。根据该团队的说法，系统的行为与理论计算非常吻合。[63]

　　 卡西米尔效应表明，量子场论允许非常小的空间区域内的能量密度相对于普通真空能量为负，并且能量密度不能任意负，因为理论在原子尺度下会失效。[64]: 175 [65][66] 著名物理学家如斯蒂芬·霍金（Stephen Hawking）[67]和基普·索恩（Kip Thorne）[68]曾推测，这种效应可能使得稳定的可穿越虫洞成为可能。

12. 另见

13. 参考文献

  1. Lamoreaux, Steven K. (2005). "The Casimir force: Background, experiments, and applications". *Reports on Progress in Physics*. 68 (1): 201–236. Bibcode:2005RPPh...68..201L. doi:10.1088/0034-4885/68/1/r04. S2CID 21131414.
  2. Mostepanenko, V M; Trunov, N N (30 November 1988). "The Casimir effect and its applications". *Soviet Physics Uspekhi*. 31 (11): 965–987. doi:10.1070/PU1988v031n11ABEH005641. ISSN 0038-5670.
  3. Klimchitskaya, G. L.; Mohideen, U.; Mostepanenko, V. M. (21 December 2009). "The Casimir force between real materials: Experiment and theory". *Reviews of Modern Physics*. 81 (4): 1827–1885. arXiv:0902.4022. Bibcode:2009RvMP...81.1827K. doi:10.1103/RevModPhys.81.1827. ISSN 0034-6861.
  4. Casimir, H. B. G.; Polder, D. (15 February 1948). "The Influence of Retardation on the London–van der Waals Forces". *Physical Review*. 73 (4): 360–372. Bibcode:1948PhRv...73..360C. doi:10.1103/PhysRev.73.360. ISSN 0031-899X.
  5. Dzyaloshinskii, I E; Lifshitz, E M; Pitaevskii, Lev P (1961). "General Theory of van der Waals' Forces". *Soviet Physics Uspekhi*. 4 (2): 153. Bibcode:1961SvPhU...4..153D. doi:10.1070/PU1961v004n02ABEH003330.
  6. Intravaia, Francesco; Behunin, Ryan (28 December 2012). "Casimir effect as a sum over modes in dissipative systems". *Physical Review A*. 86 (6): 062517. arXiv:1209.6072. Bibcode:2012PhRvA..86f2517I. doi:10.1103/PhysRevA.86.062517. ISSN 1050-2947. S2CID 119211980.
  7. Lamoreaux, S. K. (1997). "Demonstration of the Casimir Force in the 0.6 to 6 μm Range". *Physical Review Letters*. 78 (1): 5–8. Bibcode:1997PhRvL..78....5L. doi:10.1103/PhysRevLett.78.5. S2CID 25323874.
  8. E. L. Losada "Functional Approach to the Fermionic Casimir Effect" Archived 31 May 2011 at the Wayback Machine.
  9. Michael Bordag; Galina Leonidovna Klimchitskaya; Umar Mohideen (2009). "Chapter I; § 3: Field quantization and vacuum energy in the presence of boundaries". *Advances in the Casimir effect*. Oxford University Press. pp. 33 ff. ISBN 978-0-19-923874-3. Reviewed in Lamoreaux, Steve K. (2010). "Advances in the Casimir Effect Advances in the Casimir Effect, M. Bordag, G. L. Klimchitskaya, U. Mohideen, and V. M. Mostepanenko Oxford U. Press, New York, 2009. 150.00 (749 pp.). ISBN 978-0-19-923874-3". *Physics Today*. 63 (8): 50–51. Bibcode:2010PhT....63h..50B. doi:10.1063/1.3480079.
  10. Griffiths, D. J.; Ho, E. (2001). "Classical Casimir effect for beads on a string". *American Journal of Physics*. 69 (11): 1173. Bibcode:2001AmJPh..69.1173G. doi:10.1119/1.1396620.
  11. Cooke, J. H. (1998). "Casimir force on a loaded string". *American Journal of Physics*. 66 (7): 569–572. Bibcode:1998AmJPh..66..569C. doi:10.1119/1.18907.
  12. Denardo, B. C.; Puda, J. J.; Larraza, A. S. (2009). "A water wave analog of the Casimir effect". *American Journal of Physics*. 77 (12): 1095. Bibcode:2009AmJPh..77.1095D. doi:10.1119/1.3211416.
  13. Larraza, A. S.; Denardo, B. (1998). "An acoustic Casimir effect". *Physics Letters A*. 248 (2–4): 151. Bibcode:1998PhLA..248..151L. doi:10.1016/S0375-9601(98)00652-5.
  14. Astrid Lambrecht, Serge Reynaud and Cyriaque Genet (2007) "Casimir In The Nanoworld" Archived 22 November 2009 at the Wayback Machine.
  15. Genet, C.; Intravaia, F.; Lambrecht, A.; Reynaud, S. (2004). "Electromagnetic vacuum fluctuations, Casimir and Van der Waals forces" (PDF). *Annales de la Fondation Louis de Broglie*. 29 (1–2): 311–328. arXiv:quant-ph/0302072. Bibcode:2003quant.ph..2072G. Archived (PDF) from the original on 3 October 2016.
  16. "The Force of Empty Space", *Physical Review Focus*, 3 December 1998.
  17. Lambrecht, A. (1 September 2002). "The Casimir effect: a force from nothing". *Physics World*. Retrieved 17 July 2009.
  18. "American Institute of Physics News Note 1996". Archived from the original on 29 January 2008. Retrieved 28 February 2008.
  19. Jaffe, R. (2005). "Casimir effect and the quantum vacuum". *Physical Review D*. 72 (2): 021301. arXiv:hep-th/0503158. Bibcode:2005PhRvD..72b1301J. doi:10.1103/PhysRevD.72.021301. S2CID 13171179.
  20. Casimir, H. B. G. (1948). "On the attraction between two perfectly conducting plates" (PDF). *Proc. Kon. Ned. Akad. Wet.* 51: 793. Archived (PDF) from the original on 18 April 2013.
  21. Du, Z. Z.; Liu, H. M.; Xie, Y. L.; Wang, Q. H.; Liu, J.-M. (7 December 2015). "Spin Casimir effect in noncollinear quantum antiferromagnets: Torque equilibrium spin wave approach". *Physical Review B*. 92 (21): 214409. arXiv:1506.05211. Bibcode:2015arXiv150605211D. doi:10.1103/PhysRevB.92.214409. ISSN 1098-0121. S2CID 118348464.
  22. SE Rugh, H Zinkernagel; Zinkernagel (2002). "The quantum vacuum and the cosmological constant problem". *Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics*. 33 (4): 663–705. arXiv:hep-th/0012253. Bibcode:2002SHPMP..33..663R. doi:10.1016/S1355-2198(02)00033-3. S2CID 9007190.
  23. Bianchi, Eugenio; Rovelli, Carlo (2010). "Why all these prejudices against a constant?". arXiv:1002.3966 [astro-ph.CO].
  24. Schwinger, Julian; DeRaad, Lester L.; Milton, Kimball A. (1978). "Casimir effect in dielectrics". *Annals of Physics*. 115 (1): 1–23. Bibcode:1978AnPhy.115....1S. doi:10.1016/0003-4916(78)90172-0.
  25. Nikolic, Hrvoje (2016). "Proof that Casimir force does not originate from vacuum energy". *Physics Letters B*. 761: 197–202. arXiv:1605.04143. Bibcode:2016PhLB..761..197N. doi:10.1016/j.physletb.2016.08.036. S2CID 119265677.
  26. Nikolic, Hrvoje (2017). "Is zero-point energy physical? A toy model for Casimir-like effect". *Annals of Physics*. 383: 181–195. arXiv:1702.03291. Bibcode:2017AnPhy.383..181N. doi:10.1016/j.aop.2017.05.013. S2CID 118883930.
  27. For a brief summary, see the introduction in Passante, R.; Spagnolo, S. (2007). "Casimir–Polder interatomic potential between two atoms at finite temperature and in the presence of boundary conditions". *Physical Review A*. 76 (4): 042112. arXiv:0708.2240. Bibcode:2007PhRvA..76d2112P. doi:10.1103/PhysRevA.76.042112. S2CID 119651683.
  28. Ruggiero, Zimerman; Villani (1977). "Application of Analytic Regularization to the Casimir Forces" (PDF). *Revista Brasileira de Física*. 7 (3). Archived (PDF) from the original on 3 April 2015.
  29. Dzyaloshinskii, I E; Kats, E I (2004). "Casimir forces in modulated systems". *Journal of Physics: Condensed Matter*. 16 (32): 5659. arXiv:cond-mat/0408348. Bibcode:2004JPCM...16.5659D. doi:10.1088/0953-8984/16/32/003. S2CID 250897415.
  30. V. A. Parsegian, *Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists* (Cambridge Univ. Press, 2006).
  31. Rodriguez, A. W.; Capasso, F.; Johnson, Steven G. (2011). "The Casimir effect in microstructured geometries". *Nature Photonics*. 5 (4): 211–221. Bibcode:2011NaPho...5..211R. doi:10.1038/nphoton.2011.39. 综述文章。
  32. B. V. Derjaguin, I. I. Abrikosova, and E. M. Lifshitz, Quarterly Reviews, *Chemical Society*, vol. 10, 295–329 (1956).
  33. Reid, M. T. H.; White, J.; Johnson, S. G. (2011). "Computation of Casimir interactions between arbitrary three-dimensional objects with arbitrary material properties". *Physical Review A*. 84 (1): 010503(R). arXiv:1010.5539. Bibcode:2011PhRvA..84a0503R. doi:10.1103/PhysRevA.84.010503. S2CID 197461628.
  34. Sparnaay, M. J. (1957). "Attractive Forces between Flat Plates". *Nature*. 180 (4581): 334–335. Bibcode:1957Natur.180..334S. doi:10.1038/180334b0. S2CID 4263111.
  35. Sparnaay, M (1958). "Measurements of attractive forces between flat plates". *Physica*. 24 (6–10): 751–764. Bibcode:1958Phy....24..751S. doi:10.1016/S0031-8914(58)80090-7.
  36. Mohideen, U.; Roy, Anushree (1998). "Precision Measurement of the Casimir Force from 0.1 to 0.9 µm". *Physical Review Letters*. 81 (21): 4549–4552. arXiv:physics/9805038. Bibcode:1998PhRvL..81.4549M. doi:10.1103/PhysRevLett.81.4549. S2CID 56132451.
  37. Bressi, G.; Carugno, G.; Onofrio, R.; Ruoso, G. (2002). "Measurement of the Casimir Force between Parallel Metallic Surfaces". *Physical Review Letters*. 88 (4): 041804. arXiv:quant-ph/0203002. Bibcode:2002PhRvL..88d1804B. doi:10.1103/PhysRevLett.88.041804. PMID 11801108. S2CID 43354557.
  38. Klimchitskaya, G. L.; Mohideen, U.; Mostepanenko, V. M. (2009 年 12 月 21 日). "The Casimir force between real materials: Experiment and theory". *Reviews of Modern Physics*. 81 (4): 1827–1885. arXiv:0902.4022. Bibcode:2009RvMP...81.1827K. doi:10.1103/RevModPhys.81.1827. ISSN 0034-6861.
  39. Zao, J.; Marcet, Z.; Rodriguez, A. W.; Reid, M. T. H.; McCauley, A. P.; Kravchenko, I. I.; Lu, T.; Bao, Y.; Johnson, S. G.; Chan, H. B.; 等 (2013 年 5 月 14 日). "Casimir forces on a silicon micromechanical chip". *Nature Communications*. 4: 1845. arXiv:1207.6163. Bibcode:2013NatCo...4.1845Z. doi:10.1038/ncomms2842. PMID 23673630. S2CID 46359798.
  40. Lu, T.; Wang, Mingkang; Ng, C. Y.; Nikolic, M.; Chan, C. T.; Rodriguez, Alejandro; Chan, H. B.; 等 (2017 年 1 月 9 日). "Measurement of non-monotonic Casimir forces between silicon nanostructures". *Nature Photonics*. 11 (2): 97–101. arXiv:1701.02351. Bibcode:2017NaPho..11...97T. doi:10.1038/nphoton.2016.254. S2CID 119327017.
  41. Wang, Mingkang; Tang, L.; Ng, C. Y.; Messina, Riccardo; Guizal, Brahim; Crosse, J. A.; Antezza, Mauro; Chan, C. T.; Chan, H. B.; 等 (2021 年 1 月 26 日). "Strong geometry dependence of the Casimir force between interpenetrated rectangular gratings". *Nature Communications*. 12 (1): 600. arXiv:2009.02187. Bibcode:2021NatCo..12..600W. doi:10.1038/s41467-021-20891-4. PMC 7838308. PMID 33500401.
  42. Ajdari, A.; Duplantier, B.; Hone, D.; Peliti, L.; Prost, J. (1992 年 3 月). ""Pseudo-Casimir" effect in liquid crystals". *Journal de Physique II*. 2 (3): 487–501. Bibcode:1992JPhy2...2..487A. doi:10.1051/jp2:1992145. S2CID 55236741.
  43. Fulling, S. A.; Davies, P. C. W. (1976). "Radiation from a Moving Mirror in Two Dimensional Space-Time: Conformal Anomaly". *Proceedings of the Royal Society A*. 348 (1654): 393. Bibcode:1976RSPSA.348..393F. doi:10.1098/rspa.1976.0045. S2CID 122176090.
  44. "First Observation of the Dynamical Casimir Effect". *Technology Review*.
  45. Wilson, C. M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J. R.; Duty, T.; Nori, F.; Delsing, P. (2011). "Observation of the Dynamical Casimir Effect in a Superconducting Circuit". *Nature*. 479 (7373): 376–379. arXiv:1105.4714. Bibcode:2011Natur.479..376W. doi:10.1038/nature10561. PMID 22094697. S2CID 219735.
  46. "Dynamical Casimir effect in a Josephson metamaterial". *Proceedings of the National Academy of Sciences of the United States of America*.
  47. Vezzoli, S.; Mussot, A.; Westerberg, N.; Kudlinski, A.; Saleh, H. D.; Prain, A.; Biancalana, F.; Lantz, E.; Faccio, D. (2019). "Optical analogue of the dynamical Casimir effect in a dispersion-oscillating fibre". *Communications Physics*. 2 (1): 84. arXiv:1811.04262. Bibcode:2019CmPhy...2...84V. doi:10.1038/s42005-019-0183-z. S2CID 53691352.
  48. Wilczek, F.; Linder, E. V.; Good, M.R.R. (2020). "Moving mirror model for quasithermal radiation fields". *Physical Review D*. 101 (2): 025012. Bibcode:2020PhRvD.101b5012G. doi:10.1103/PhysRevD.101.025012. hdl:1721.1/125524. OSTI 1635008. S2CID 213899274.
  49. Birrell, N. D.; Davies, P. C. W. (1982). *Quantum Fields in Curved Space*. Cambridge Monographs on Mathematical Physics. Cambridge University Press. doi:10.1017/CBO9780511622632. ISBN 978-0-521-23385-9.
  50. Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. (1961). "The general theory of van der Waals forces". *Advances in Physics*. 10 (38): 165. Bibcode:1961AdPhy..10..165D. doi:10.1080/00018736100101281.
  51. Munday, J.N.; Capasso, F.; Parsegian, V.A. (2009). "Measured long-range repulsive Casimir–Lifshitz forces". *Nature*. 457 (7226): 170–3. Bibcode:2009Natur.457..170M. doi:10.1038/nature07610. PMC 4169270. PMID 19129843.
  52. Highfield, Roger (2007 年 8 月 6 日). "Physicists have 'solved' mystery of levitation". *The Daily Telegraph*. London. Archived from the original on 13 May 2008. Retrieved 28 April 2010.
  53. Leonhardt, Ulf; Philbin, Thomas G. (2007 年 8 月). "Quantum levitation by left-handed metamaterials". *New Journal of Physics*. 9 (8): 254. arXiv:quant-ph/0608115. Bibcode:2007NJPh....9..254L. doi:10.1088/1367-2630/9/8/254.
  54. Milton, K. A.; Abalo, E. K.; Parashar, Prachi; Pourtolami, Nima; Brevik, Iver; Ellingsen, Simen A. (2012). "Repulsive Casimir and Casimir–Polder Forces". *J. Phys. A*. 45 (37): 4006. arXiv:1202.6415. Bibcode:2012JPhA...45K4006M. doi:10.1088/1751-8113/45/37/374006. S2CID 118364958.
  55. Jiang, Qing-Dong; Wilczek, Frank (2019 年 3 月 4 日). "Chiral Casimir forces: Repulsive, enhanced, tunable". *Physical Review B*. 99 (12): 125403. arXiv:1805.07994. Bibcode:2019PhRvB..99l5403J. doi:10.1103/PhysRevB.99.125403. S2CID 67802144.
  56. Boyer, Timothy H. (1968 年 10 月 25 日). "Quantum Electromagnetic Zero-Point Energy of a Conducting Spherical Shell and the Casimir Model for a Charged Particle". *Physical Review*. 174 (5): 1764–1776. Bibcode:1968PhRv..174.1764B. doi:10.1103/PhysRev.174.1764.
  57. Sanderson, Katharine (2009 年 1 月 7 日). "Quantum force gets repulsive". *Nature*: news.2009.4. doi:10.1038/news.2009.4. ISSN 0028-0836.
  58. Capasso, F.; Munday, J.N.; Iannuzzi, D.; Chan, H.B. (2007). "Casimir forces and quantum electrodynamical torques: physics and nanomechanics". *IEEE Journal of Selected Topics in Quantum Electronics*. 13 (2): 400. Bibcode:2007IJSTQ..13..400C. doi:10.1109/JSTQE.2007.893082. S2CID 32996610.
  59. Serry, F.M.; Walliser, D.; MacLay, G.J. (1995). "The anharmonic Casimir oscillator (ACO)-the Casimir effect in a model microelectromechanical system" (PDF). *Journal of Microelectromechanical Systems*. 4 (4): 193. doi:10.1109/84.475546. Archived (PDF) from the original on 13 March 2006.
  60. Serry, F. M.; Walliser, D.; Maclay, G. J. (1995). "The anharmonic Casimir oscillator (ACO)-the Casimir effect in a model microelectromechanical system" (PDF). *Journal of Microelectromechanical Systems*. 4 (4): 193–205. doi:10.1109/84.475546. Archived from the original (PDF) on 13 March 2006. Retrieved 24 October 2016.
  61. Serry, F. Michael; Walliser, Dirk; Maclay, G. Jordan (1998). "The role of the Casimir effect in the static deflection and stiction of membrane strips in microelectromechanical systems (MEMS)" (PDF). *Journal of Applied Physics*. 84 (5): 2501–2506. Bibcode:1998JAP....84.2501S. doi:10.1063/1.368410. Retrieved 24 October 2016.
  62. Bordag, M; Klimchitskaya, G. L.; Mohideen, U.; Mostepanenko, V. M. (2009). *Advances in the Casimir Effect*. Oxford: Oxford University Press. ISBN 978-0-19-923874-3. LCCN 2009279136. OCLC 319209483.
  63. Chan, H. B.; Aksyuk, V. A.; Kleiman, R. N.; Bishop, D. J.; Capasso, F. (2001). "Quantum Mechanical Actuation of Microelectromechanical Systems by the Casimir Force" (PDF). *Science*. 291 (5510): 1941–1944. Bibcode:2001Sci...291.1941C. doi:10.1126/science.1057984. PMID 11239149. S2CID 17072357.
  64. Everett, Allen; Roman, Thomas (2012). *Time Travel and Warp Drives*. University of Chicago Press. p. 167. ISBN 978-0-226-22498-5.
  65. Sopova, V.; Ford, L. H. (2002). "The Energy Density in the Casimir Effect". *Physical Review D*. 66 (4): 045026. arXiv:quant-ph/0204125. Bibcode:2002PhRvD..66d5026S. doi:10.1103/PhysRevD.66.045026. S2CID 10649139.
  66. Ford, L. H.; Roman, Thomas A. (1995). "Averaged Energy Conditions and Quantum Inequalities". *Physical Review D*. 51 (8): 4277–4286. arXiv:gr-qc/9410043. Bibcode:1995PhRvD..51.4277F. doi:10.1103/PhysRevD.51.4277. PMID 10018903. S2CID 7413835.
  67. "Space and Time Warps". *Hawking.org.uk*. Archived from the original on 10 February 2012. Retrieved 11 November 2010.
  68. Morris, Michael; Thorne, Kip; Yurtsever, Ulvi (1988). "Wormholes, Time Machines, and the Weak Energy Condition" (PDF). *Physical Review Letters*. 61 (13): 1446–1449. Bibcode:1988PhRvL..61.1446M. doi:10.1103/PhysRevLett.61.1446. PMID 10038800. Archived (PDF) from the original on 9 July 2011.

14. 进一步阅读

入门阅读：

论文、书籍与讲座

温度依赖性

15. 外部链接

                     

© 小时科技 保留一切权利