卡迈克尔函数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数论（数学的一个分支）中，正整数 $n$ 的卡迈克尔函数 $\lambda(n)$ 定义为满足下列条件的最小正整数 $m$： $$ a^{m} \equiv 1 \pmod{n}~ $$ 其中 $a$ 为任意与 $n$ 互素的整数。从代数的角度来看，$\lambda(n)$ 是模 $n$ 的整数乘法群的指数。由于这是一个有限阿贝尔群，必然存在一个元素，其阶等于该指数 $\lambda(n)$。这样的元素被称为模 $n$ 的本原 $\lambda$-根（primitive $\lambda$-root modulo $n$）。

图
图 1：卡迈克尔 λ 函数：$1 \le n \le 1000$ 时的 $\lambda(n)$（与欧拉 φ 函数对比）

　　 卡迈克尔函数以美国数学家罗伯特·卡迈克尔的名字命名，他于 1910 年首次给出了这一函数的定义 \(^\text{[1]}\)。它也被称为卡迈克尔 $\lambda$ 函数、约化欧拉函数以及最小通用指数函数。

　　 模 $n$ 的整数乘法群的阶是 $\varphi(n)$，其中 $\varphi$ 是**欧拉函数**。由于有限群中任一元素的阶都会整除群的阶，所以 $\lambda(n)$ 一定整除 $\varphi(n)$。

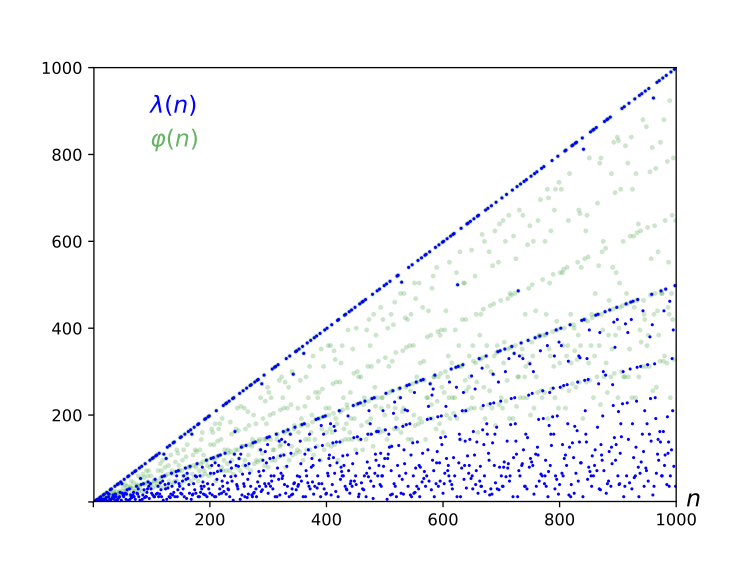
　　 下表比较了 $\lambda(n)$（OEIS 数列 A002322）与 $\varphi(n)$ 的前 36 个值（当二者不同的时候，$\varphi(n)$ 用粗体表示；使它们不同的那些 $n$ 的值列在 OEIS 数列 A033949 中）。

图
图 2

1. 数值例子

2. λ(n) 的递推公式

　　 质数幂的卡迈克尔 $\lambda$ 函数可以用欧拉函数表示。任何不是 1 且不是质数幂的整数，都可以唯一地分解为不同质数幂的乘积，此时该数的 $\lambda$ 值等于这些质数幂的 $\lambda$ 值的最小公倍数。具体来说，$\lambda(n)$ 由以下递推式给出： $$ \lambda(n) = \begin{cases} \varphi(n), & \text{如果 } n \text{ 是 1、2、4，或奇质数幂}, \\[6pt] \dfrac{1}{2} \varphi(n), & \text{如果 } n = 2^{r},\ r \geq 3, \\[8pt] \operatorname{lcm}\bigl(\lambda(n_{1}),\lambda(n_{2}),\dots,\lambda(n_{k})\bigr), & \text{如果 } n = n_{1} n_{2} \dots n_{k}, \ \text{且 } n_{1},n_{2},\dots,n_{k} \text{ 是不同质数的幂}. \end{cases}~ $$ 其中，质数幂 $p^r$（$p$ 为质数且 $r \geq 1$）的欧拉函数为： $$ \varphi(p^{r}) = p^{r-1}(p - 1)~ $$

3. 卡迈克尔定理

　　 卡迈克尔证明了两个定理，它们共同确立了这样一个事实：如果将 $\lambda(n)$ 按照上一节的递推公式来定义，那么它就满足引言中所述的性质——即它是满足以下条件的最小正整数 $m$：$a^{m} \equiv 1 \pmod{n}$ 对于所有与 $n$ 互素的整数 $a$，上述同余式都成立。

　　 定理 1 —— 如果 $a$ 与 $n$ 互素，则：$a^{\lambda(n)} \equiv 1 \pmod{n}$。\(^\text{[2]}\)

　　 这意味着：模 $n$ 的整数乘法群中每个元素的阶都整除 $\lambda(n)$。卡迈克尔将这样一种元素 $a$ 称为模 $n$ 的本原 $\lambda$-根（primitive $\lambda$-root modulo $n$）：它的最小正整数指数，使得 $a^{\lambda(n)} \equiv 1 \pmod{n}$\(^\text{[3]}\)（不要与模 $n$ 的本原根混淆，卡迈克尔有时会称其为模 $n$ 的本原 $\varphi$-根）。

　　 定理 2 —— 对于任意正整数 $n$，都存在一个模 $n$ 的本原 $\lambda$-根。此外，如果 $g$ 是这样一个根，那么所有与 $g$ 的幂同余的本原 $\lambda$-根的个数为：$\varphi\bigl(\lambda(n)\bigr)$。\(^\text{[4]}\)

　　 如果 $g$ 是定理所保证存在的模 $n$ 的本原 $\lambda$-根之一，那么同余式 $g^{m} \equiv 1 \pmod{n}$ 在正整数范围内没有小于 $\lambda(n)$ 的解。这说明不存在正整数 $m < \lambda(n)$，能使得对于所有与 $n$ 互素的 $a$，都满足 $a^{m} \equiv 1 \pmod{n}$。

　　 定理 2 的第二条结论并不意味着模 $n$ 的所有本原 $\lambda$-根都与某一个本原根 $g$ 的幂同余 \(^\text{[5]}\)。例如，当 $n = 15$ 时，$\lambda(n) = 4$，而 $\varphi(n) = 8$，$\varphi(\lambda(n)) = 2$。模 15 的本原 $\lambda$-根共有 4 个，分别是 2、7、8 和 13，因为：$1 \equiv 2^{4} \equiv 8^{4} \equiv 7^{4} \equiv 13^{4} \pmod{15}$。其中 2 和 8 互为幂同余，7 和 13 互为幂同余，但 7 和 13 都不与 2 或 8 的幂同余，反之亦然。模 15 的乘法群中的另外四个元素——1、4（满足 $4 \equiv 2^{2} \equiv 8^{2} \equiv 7^{2} \equiv 13^{2} \pmod{15}$）、11 和 14——都不是模 15 的本原 $\lambda$-根。

　　 再看一个对比性的例子：当 $n = 9$ 时，$\lambda(n) = \varphi(n) = 6$，且 $\varphi(\lambda(n)) = 2$。模 9 的本原 $\lambda$-根有两个，分别是 2 和 5，并且它们互为对方的五次幂同余。它们同时也是模 9 的本原 $\varphi$-根。

4. 卡迈克尔函数的性质

　　 在本节中，若存在一个整数 $k$，使得 $$ n = k m,~ $$ 则称整数 $n$ 可被非零整数 $m$ 整除，记作： $$ m \mid n~ $$

λ(n) 最小性的推论

　　 假设对于所有与 $n$ 互素的整数 $a$，都有 $a^{m} \equiv 1 \pmod{n}$，那么 $\lambda(n) \mid m$。

　　 证明：

　　 设 $m = k \lambda(n) + r, \quad 0 \le r < \lambda(n)$，则对于所有与 $n$ 互素的整数 $a$，有： $$ a^{r} = 1^{k} \cdot a^{r} \equiv \left(a^{\lambda(n)}\right)^{k} \cdot a^{r} = a^{k\lambda(n) + r} = a^{m} \equiv 1 \pmod{n}~ $$ 由于 $r < \lambda(n)$ 且 $\lambda(n)$ 是使得上述同余式对所有与 $n$ 互素的 $a$ 成立的最小正整数指数，因此必须有 $r = 0$。

$\lambda(n)$ 整除 $\varphi(n)$

　　 这可以由初等群论推出，因为任何有限群的指数都必须整除该群的阶。$\lambda(n)$ 是模 $n$ 的整数乘法群的指数，而 $\varphi(n)$ 是该群的阶。

　　 特别地，当该乘法群是循环群时（因为存在本原根），二者相等。这种情况发生在奇质数幂的情形下。

　　 因此，我们可以把卡迈克尔定理看作是对欧拉定理的一个强化。

可整除性

　　 $$ a \mid b \ \Rightarrow \ \lambda(a) \mid \lambda(b)~ $$ 证明：

　　 由定义可知，对于任意满足 $\gcd(k, b) = 1$（因此也有 $\gcd(k, a) = 1$）的整数 $k$，有：$b \mid \bigl(k^{\lambda(b)} - 1\bigr)$，因此也有：$a \mid \bigl(k^{\lambda(b)} - 1\bigr)$。这说明对于所有与 $a$ 互素的 $k$，都有：$k^{\lambda(b)} \equiv 1 \pmod{a}$。根据前面已证明的最小性推论，我们得到：$ \lambda(a) \mid \lambda(b)$。

复合性质

　　 对于所有正整数 $a$ 和 $b$，都有： $$ \lambda\bigl(\mathrm{lcm}(a, b)\bigr) = \mathrm{lcm}\bigl(\lambda(a), \lambda(b)\bigr)~ $$ 这是卡迈克尔函数递推公式的直接推论。

指数循环长度

　　 如果 $r_{\mathrm{max}} = \max_{i} \{ r_{i} \}$ 是整数 $n$ 的质因数分解 $n = p_{1}^{r_{1}} p_{2}^{r_{2}} \cdots p_{k}^{r_{k}}$ 中最大的指数，那么对于所有整数 $a$（包括与 $n$ 不互素的 $a$）以及所有 $r \ge r_{\mathrm{max}}$，都有： $$ a^{r} \equiv a^{\lambda(n) + r} \pmod{n}~ $$ 特别地，当 $n$ 是平方因子自由数（square-free，$r_{\mathrm{max}} = 1$）时，对于所有 $a$ 都有： $$ a \equiv a^{\lambda(n) + 1} \pmod{n}~ $$

平均值

　　 对于任意 $n \ge 16$\(^\text{[6][7]}\)： $$ \frac{1}{n} \sum_{i \le n} \lambda(i) = \frac{n}{\ln n} e^{B \,(1 + o(1)) \,\frac{\ln \ln n}{\ln \ln \ln n}}~ $$ （下文称为埃尔德什近似，Erdős approximation），其中常数 $$ B := e^{-\gamma} \prod_{p \in \mathbb{P}} \left( 1 - \frac{1}{(p - 1)^{2}(p + 1)} \right) \approx 0.34537~ $$

　　 $\gamma \approx 0.57721$ 为欧拉–马歇罗尼常数。

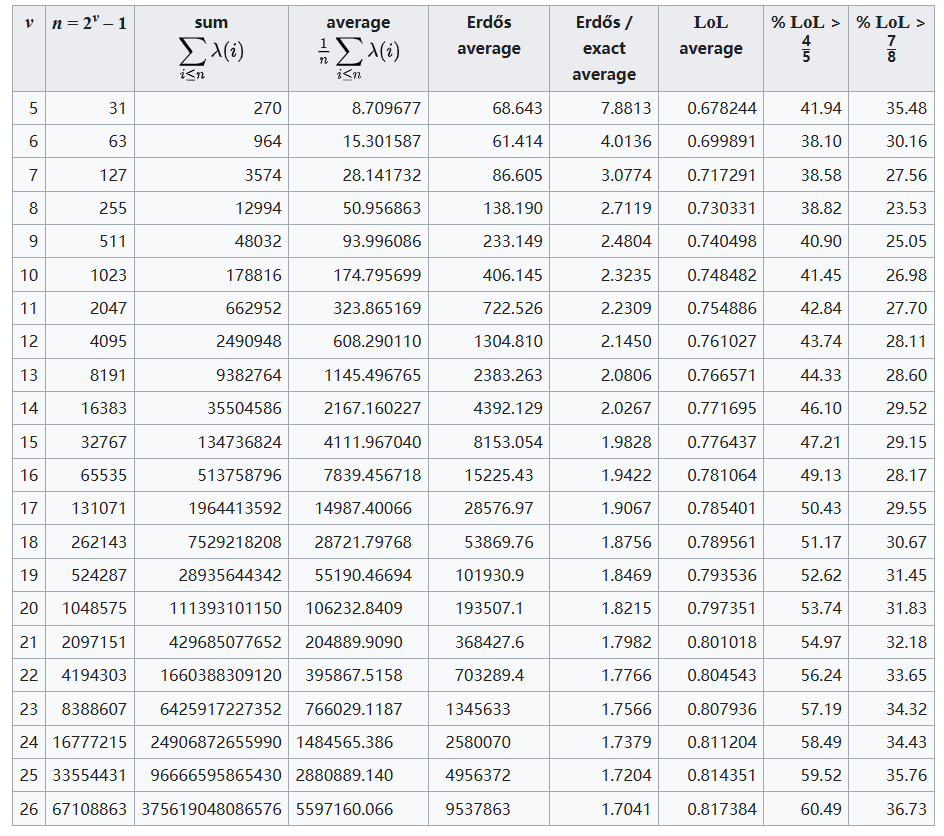
　　 下表给出了 $\lambda$ 函数前 $2^{26} - 1 = 67\,108\,863$ 个值的概览，包括其精确平均值和埃尔德什近似值。

　　 另外，还给出了一个更易计算的 “对数比对数” 值（LoL 值）： $$ \mathrm{LoL}(n) := \frac{\ln \lambda(n)}{\ln n}~ $$ 其中：

　　 在表格中，第 26 行

　　 这意味着，大多数 $\lambda$ 值在输入 $n$ 的长度 $l := \log_{2} n$ 上是指数级的，具体为： $$ \left( 2^{\frac{4}{5}} \right)^{l} = 2^{\frac{4l}{5}} = \left( 2^{l} \right)^{\frac{4}{5}} = n^{\frac{4}{5}}~ $$

图
图 3

主导区间

　　 对于任意整数 $N$，以及除了 $o(N)$\(^\text{[8]}\) 之外的所有正整数 $n \le N$（即 “主导性的大多数”），都有： $$ \lambda(n) = \frac{n}{(\ln n)^{\ln \ln \ln n + A + o(1)}}~ $$ 其中常数 \(^\text{[7]}\)： $$ A := -1 + \sum_{p \in \mathbb{P}} \frac{\ln p}{(p - 1)^{2}} \approx 0.2269688~ $$

下界

　　 对于任意足够大的数 $N$ 以及任意 $\Delta \ge (\ln \ln N)^{3}$，在所有 $n \le N$ 的正整数中，满足 $\lambda(n) \le n e^{-\Delta}$\(^\text{[9]}\) 的个数至多为： $$ N \exp\left( -0.69 (\Delta \ln \Delta)^{\frac{1}{3}} \right)~ $$

最小阶

　　 对于任意正整数序列 $n_{1} < n_{2} < n_{3} < \cdots$ 任意常数 $0 < c < \frac{1}{\ln 2}$，以及任意足够大的 $i$\(^\text{[10][11]}\)： $$ \lambda(n_{i}) > \left( \ln n_{i} \right)^{c \, \ln \ln \ln n_{i}}~ $$

小值

　　 对于任意常数 $c$ 和任意足够大的正数 $A$，存在整数 $n > A$ 使得 \(^\text{[11]}\)： $$ \lambda(n) < \left( \ln A \right)^{c \, \ln \ln \ln A}~ $$ 此外，$n$ 的形式为： $$ n = \prod_{\substack{q \in \mathbb{P} \\ (q - 1) \mid m}} q~ $$ 其中 $m$ 是平方因子自由整数，且 $m < (\ln A)^{c \, \ln \ln \ln A}$\(^\text{[10]}\)。

函数的值域

　　 卡迈克尔函数取值的集合，其计数函数为 \(^\text{[12]}\)： $$ \frac{x}{(\ln x)^{\eta + o(1)}},~ $$ 其中： $$ \eta = 1 - \frac{1 + \ln \ln 2}{\ln 2} \approx 0.08607~ $$

5. 在密码学中的应用

　　 卡迈克尔函数在密码学中具有重要意义，尤其是在 RSA 加密算法 中的应用。

6. 定理 1 的证明

　　 当 $n = p$ 为质数时，定理 1 等价于费马小定理： $$ a^{p-1} \equiv 1 \pmod{p} \qquad \text{对于所有与 } p \text{ 互素的 } a~ $$ 对于质数幂 $p^{r}$（$r > 1$），如果存在整数 $h$ 使得： $$ a^{p^{\,r-1}(p - 1)} = 1 + h p^{r},~ $$ 那么将等式两边同时取 $p$ 次幂，得到： $$ a^{p^{\,r}(p - 1)} = 1 + h' p^{r+1},~ $$ 其中 $h'$ 是某个整数。由归纳法可得：$a^{\varphi(p^{r})} \equiv 1 \pmod{p^{r}}$ 对所有与 $p$ 互素（因此也与 $p^{r}$ 互素）的 $a$ 都成立。这就证明了定理在 $n = 4$ 或任意奇质数幂的情形下成立。

对 2 的高次幂情形的结果强化

　　 对于与（2 的幂）互素的 $a$，可写成 $a = 1 + 2h_{2}$ 其中 $h_{2}$ 为某个整数。于是： $$ a^{2} = 1 + 4h_{2}(h_{2} + 1) = 1 + 8 \binom{h_{2} + 1}{2} =: 1 + 8h_{3},~ $$ 其中 $h_{3}$ 为整数。取 $r = 3$，可写作： $$ a^{2^{\,r-2}} = 1 + 2^{r} h_{r}~ $$ 将等式两边平方得： $$ a^{2^{\,r-1}} = \left( 1 + 2^{r} h_{r} \right)^{2} = 1 + 2^{r+1} \left( h_{r} + 2^{r-1} h_{r}^{2} \right) =: 1 + 2^{r+1} h_{r+1},~ $$ 其中 $h_{r+1}$ 为整数。由归纳法可得： $$ a^{2^{\,r-2}} = a^{\frac12 \varphi(2^{r})} \equiv 1 \pmod{2^{r}}~ $$ 对所有 $r \ge 3$ 且与 $2^{r}$ 互素的 $a$ 都成立 \(^\text{[13]}\)。

含有多个质因子的整数

　　 根据唯一分解定理，任意 $n > 1$ 都可以唯一地写成： $$ n = p_{1}^{r_{1}} p_{2}^{r_{2}} \cdots p_{k}^{r_{k}}~ $$ 其中 $p_{1} < p_{2} < \dots < p_{k}$ 是质数，$r_{1}, r_{2}, \dots, r_{k}$ 是正整数。质数幂情形的结论表明，对于 $1 \le j \le k$： $$ a^{\lambda\left(p_{j}^{r_{j}}\right)} \equiv 1 \pmod{p_{j}^{r_{j}}}~ $$ 对所有与 $n$ 互素（因此也与 $p_{i}^{r_{i}}$ 互素）的 $a$ 都成立。

　　 由此可知： $$ a^{\lambda(n)} \equiv 1 \pmod{p_{j}^{r_{j}}}~ $$ 对所有与 $n$ 互素的 $a$ 都成立，其中根据递推公式： $$ \lambda(n) = \mathrm{lcm}\bigl(\lambda(p_{1}^{r_{1}}), \lambda(p_{2}^{r_{2}}), \dots, \lambda(p_{k}^{r_{k}})\bigr)~ $$ 由中国剩余定理可知： $$ a^{\lambda(n)} \equiv 1 \pmod{n}~ $$ 对所有与 $n$ 互素的 $a$ 都成立。

7. 另见

8. 注释

  1. Carmichael, Robert Daniel（1910），“关于一个新的数论函数的说明”，《美国数学学会会刊》，第 16 卷（第 5 期）：232–238，doi:10.1090/S0002-9904-1910-01892-9。
  2. Carmichael（1914），第 40 页。
  3. Carmichael（1914），第 54 页。
  4. Carmichael（1914），第 55 页。
  5. Carmichael（1914），第 56 页。
  6. Erdős（1991），定理 3。
  7. Sándor & Crstici（2004），第 194 页。
  8. Erdős（1991），定理 2，3. 正常阶，第 365 页。
  9. Friedlander（2001），定理 5。
  10. Erdős（1991），定理 1。
  11. Sándor & Crstici（2004），第 193 页。
  12. Ford, Kevin；Luca, Florian；Pomerance, Carl（2014 年 8 月 27 日），“卡迈克尔 λ 函数的值域”，《代数与数论》，第 8 卷（第 8 期）：2009–2026，arXiv:1408.6506，doi:10.2140/ant.2014.8.2009，S2CID 50397623。
  13. Carmichael（1914），第 38–39 页。

9. 参考文献

                     

© 保留一切权利