Julia 类型的参数化

贡献者： xzllxls

　　本文授权转载自郝林的《Julia 编程基础》。原文链接：第 7 章参数化类型。

7.1 类型的参数化

　　参数化（parametric）是 Julia 类型系统中的一个非常重要且强大的特性。它允许类型自身包含参数，并使得一个这样的类型就可以代表整个类型族群。像 Ref{T} 这样的参数化类型，可以代表的类型的数量是无限的，因为我们可以用任何一个类型的名称替换掉 T，从而表示一种确定的（或者说具体的）类型，如 Ref{String}。进一步讲，随着类型中参数值的不同，这个类型的字面量就可以表示该类型族群中的某一个特定的类型。顺便说一下，我有时只会写出参数化类型的名称，而省略掉后面的花括号。这主要是为了简化描述和节约篇幅。到了后面我们会看到，这种表示方式依然是合法的。

　　 Julia 已经预定义了不少的参数化类型。我们在前面已经见过几个，包括 Ref、Union、Complex 和 SubString 等。对它们的进一步说明如下：

Ref{T}：它是专门用来做引用的类型。要想让它成为某一个类型的引用类型，我们就需要在其花括号中填入那个类型的名称。例如，Ref{UInt32} 就表示针对 UInt32 类型的引用类型。
Union{Types...}：这个类型的花括号中可以有多个类型名称。这使它可以表示为针对那些类型的联合类型，从而让那些类型的值都成为这个联合类型的实例。例如，Union{Integer, AbstractString} 就联合了 Integer 类型和 AbstractString 类型，从而使整数值和字符串值都变成了它的实例。
Complex{T<:Real}：代表复数的的类型。因为复数的实部和虚部都必须是实数，所以 Complex 类型的参数一定要是 Real\verb 类型的子类型。
SubString{T<:AbstractString}：代表子字符串的类型。由于子字符串值只能基于字符串值创建，因此 SubString 类型的参数必须继承自 AbstractString。

　　可以看到，前两个参数化类型对其参数都没有做显式的约束。也就是说，它们的参数值可以是任意的类型。当然，我们是可以对类型的参数做出约束的。

　　我们之前已经讲过操作符 <:。在类型定义中，它用于表示当前类型直接继承自哪一个抽象类型。它也可以与两个类型字面量构成一个表达式，以判断这两个类型之间是否存在直接或间接的继承关系。而在类型的参数定义中，<: 则用来表明参数值的有效范围，或者说参数值必须是哪一个类型的（直接或间接的）子类型。由于一个类型也是它自己的子类型，所以这里的有效范围也会包含处于 <: 右侧的那个类型。

　　后两个参数化类型都在它们的花括号中对其参数进行了约束。更确切地说，它们都对其类型参数（type parameter）的上限进行了定义。

　　我们在这里回顾这几个参数化类型，是为了帮助你重温对这种类型的宏观认识。这算是一个热身。接下来，我们将要说明怎样定义参数化类型。

　　 7.1.1 基本特征

　　我们之前说过，参数化类型就相当于一种对数据结构的泛化定义。因此，它也常被称为泛化类型，简称泛型。此种类型的奥秘就藏在紧随类型名称之后的那对花括号当中。

　　对于一个参数化类型，比如 Ref{T}，我们称其花括号中的英文字母 T（Type 的缩写）为类型参数。然而，这个字母只是一个占位符而已，用于表示这个位置上需要一个具体的参数值（别忘了，类型也是一种值）。原则上，这个占位符的名称可以是任何一个或多个可打印的 Unicode 字符。不过，按照惯例，英文字母 T 仍然是这里的首选。

　　 Julia 并没有对一个类型可以拥有多少个参数做出限制。不过，类型一旦定义完成，其类型参数的个数就会固定下来，并且不可再被更改。而 Union{Types...} 类型着实是一个特例，因为 Julia 并没有限制我们使用它联合多少个类型。它甚至还可以不联合任何类型，即 Union{}。同样特殊的还有代表元组类型的 Tuple{Types...}。有些可惜，作为 Julia 程序开发者的我们是无法编写这样的参数化类型的。

　　那么我们可以编写什么样的参数化类型呢？请接着往下看。

　　 7.1.2 参数化复合类型

　　参数化的复合类型应该是我们最常定义的一种参数化类型。如果我们想为抽屉这样的物件建立程序模型，那么可以这样来做：

julia> mutable struct Drawer{T}
           content::T
       end

　　理想状况下，一个足够大的抽屉可以容纳任何物品。所以我并没有对类型参数 T 进行约束。此外，我只为这个复合类型编写了一个字段 content，其类型同样是 T。

　　通常，一个复合类型的类型参数总是要被用在这个类型的内部的，否则也就没有必要为它定义类型参数了。对于 Drawer 类型，什么种类的物品可以被放进抽屉，恰恰取决于其类型参数的值是什么。比如，Drawer{String} 类型的类型参数已经确定，那么它的字段 content 的类型肯定也是 String。所以，我们只能把 String 类型的 “物品” 放到这类抽屉里：

julia> drawer1 = Drawer{String}("a kind of goods")
Drawer{String}("a kind of goods")

julia> drawer1.content = 'G'
ERROR: MethodError: Cannot `convert` an object of type Char
 to an object of type String
# 省略了一些回显的内容。

julia>

　　这里有一个特别之处，像 Drawer{T} 这样的表示方式只能被用在它的定义当中。如果我们想在其他地方指代这个参数化类型，那么只写出它的名称 Drawer 就好了。或者说，在其定义之外的任何地方，Drawer{T} 都只能用于表示该参数化类型的某个确定类型（如 Drawer{String}）。所以，这时的 T 必须被替换为一个已声明的类型名称。对比如下：

julia> Drawer{T} 
ERROR: UndefVarError: T not defined
# 省略了一些回显的内容。

julia> Drawer
Drawer

julia>

　　另外，由于参数化类型可以代表整个类型族群，而它的每一个确定类型都是这个类型族群中的一员。因此，参数化类型本身是它的所有确定类型的超类型。例如：

julia> Drawer{String} <: Drawer
true

julia> Drawer{Char} <: Drawer
true

julia> Drawer{Int} <: Drawer
true

julia>

　　注意，这是除了使用操作符 <: 以外的另一种可以形成继承关系的声明方式。

　　让我们再回到抽屉的话题上来。我们都知道，很多家具都有抽屉。无论是家用的还是商用的都是如此。如果这里指的是商用展柜中的抽屉，那我们还可以接着构建模型：

julia> mutable struct Showcase{T}
           drawer1::Drawer{T}
           drawer2::Drawer{T}
       end

julia>

　　上面这个展柜有两个抽屉。显然，如果这是一个首饰的展柜，那么它的抽屉里就只能放置首饰。但如果这是一个玩具展柜，那这两个抽屉里就只会放置一些玩具。所以，在确定的参数化类型 Showcase{String} 中，drawer1 和 drawer2 的类型都只会是 Drawer{String}。示例如下：

julia> showcase1 = Showcase{String}(Drawer("goods1"), Drawer("goods2"))
Showcase{String}(Drawer{String}("goods1"), Drawer{String}("goods2"))

julia>

　　可以看到，我在实例化 Showcase{String} 类型的时候并没有在类型名称 Drawer 之后编写花括号。但是，Julia 依然知道我们是在构建 Drawer{String} 类型的值。这要感谢 Julia 的类型推断。实际上，在这种情况下，我们连 Showcase 后面的花括号都可以省略掉：

julia> showcase1 = Showcase(Drawer("goods1"), Drawer("goods2"))
Showcase{String}(Drawer{String}("goods1"), Drawer{String}("goods2"))

julia>

　　 Julia 可以根据我们给予的 "goods1" 和 "goods2" 推断出这里的 Drawer 和 Showcase 的类型参数为 String。

　　现在，假设这就是一个首饰的展柜，那么我们需要先对首饰进行一些定义：

julia> abstract type Jewelry end

julia> struct Necklace <: Jewelry end

julia> struct Ring <: Jewelry end

julia>

　　我定义了代表首饰的抽象类型 Jewelry，还定义了该类型的子类型 Necklace（项链）和 Ring（戒指）。为了尽量简单，我们不去关心这些首饰的具体特征以及它们的定价。所以，我没有为 Necklace 和 Ring 添加任何字段。

　　有了前面这些定义，我们就可以开始为首饰店建模了：

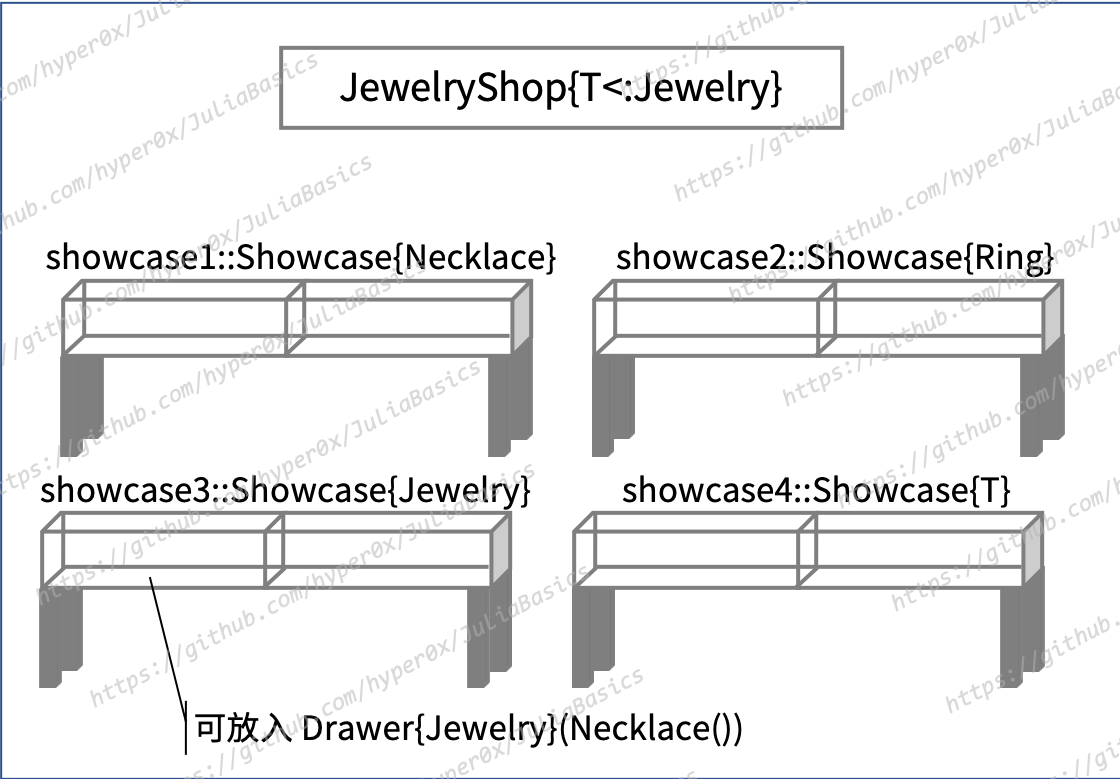
julia> mutable struct JewelryShop{T<:Jewelry}
           showcase1::Showcase{Necklace}
           showcase2::Showcase{Ring}
           showcase3::Showcase{Jewelry}
           showcase4::Showcase{T}
       end

julia>

　　在这个店铺中，第 1 个展柜专用于放置项链，第 2 个展柜专用于放置戒指。而第 3 个展柜和第 4 个展柜都是机动的展柜。我们可以根据实际需要确定它们的用途。

图 1：图 7-1 首饰店类型的示意

　　不过要注意，虽然我为 JewelryShop 的类型参数做了约束，使该参数的值必须是 Jewelry 的子类型，但 showcase3 和 showcase4 这两个字段的类型仍然是不同的。对于 showcase3，无论 JewelryShop 的具体参数值是什么，它都代表可以放置任何首饰的展柜。而 showcase4 就不同了，它可以放置哪种首饰完全取决于 JewelryShop 的具体参数值。

　　另外还要注意，虽然复合类型 Necklace 和 Ring 都是抽象类型 Jewelry 的子类型，但是基于它们的参数化类型之间却不存在这样的继承关系。比如，Drawer{Necklace} 和 Drawer{Ring} 都肯定不是 Drawer{Jewelry} 的子类型。同理，Showcase{Necklace} 和 Showcase{Ring} 也都不是 Showcase{Jewelry} 的子类型。代码演示如下：

julia> Drawer{Necklace} <: Drawer{Jewelry},
 Drawer{Ring} <: Drawer{Jewelry}

(false, false)

julia> Showcase{Necklace} <: Showcase{Jewelry}, 
Showcase{Ring} <: Showcase{Jewelry}

(false, false)

julia>

　　这种特性被称为非转化（invariant）。也就是说，对于这些确定的参数化类型，不会由于其参数值之间存在继承关系，就形成继承关系。与之相对的特性有协变（covariance）和逆变（contravariance）。

　　我们在实例化 Showcase{Jewelry} 的时候就可以明显地感知到这一特性。像下面这样构建它的值是不行的：

julia> Showcase{Jewelry}(Drawer(Necklace()), Drawer(Ring()))
ERROR: MethodError: Cannot `convert` an object of type Drawer{Necklace} 
to an object of type Drawer{Jewelry}
# 省略了一些回显的内容。

julia>

　　依据提示可知，报错的原因是 Drawer{Necklace} 类型的值无法被转换成 Drawer{Jewelry} 类型的值。对于像 Showcase{Jewelry} 这样的确定的参数化类型，Julia 会为它自动生成一个全名（即携带花括号的名称）相同的构造函数。这个构造函数接受的参数与该类型的字段一一对应，但参数的类型并没有被约束。

　　也就是说，我们在使用这样的构造函数时，必须提供数量与该类型的字段数相同的参数值，但参数值的类型可以是任意的。Julia 一旦发现参数值的类型与对应字段的类型不符，就会试图通过调用 convert 函数进行参数类型转换。如果转换不成功，那么就会直接报错。

　　现在我们知道了，Showcase{Jewelry} 类型的两个字段都是 Drawer{Jewelry} 类型的。但是，我们传给它的构造函数的参数值 Drawer(Necklace()) 和 Drawer(Ring()) 却分别是 Drawer{Necklace} 类型和 Drawer{Ring} 类型的。在这种情况下，Julia 会试图进行参数类型转换。可是，转换失败了，因为 Drawer{Necklace} 和 Drawer{Ring} 都不是 Drawer{Jewelry} 的子类型。错误由此产生。

　　不过，我们只要稍加改动就可以使这段代码合法化：

julia> Showcase{Jewelry}(Drawer{Jewelry}(Necklace()),
 Drawer{Jewelry}(Ring()))

Showcase{Jewelry}(Drawer{Jewelry}(Necklace()),
 Drawer{Jewelry}(Ring()))

julia>

　　注意，我们这次传给 Showcase{Jewelry} 函数的是两个 Drawer{Jewelry} 类型的值。因为 Jewelry 是一个抽象类型，所以它本身不能被实例化。但由于 Necklace 和 Ring 都是它的子类型，因此把这两个类型（之一）的值传给 Drawer{Jewelry} 的构造函数是完全没有问题的。这与上述参数化类型之间的关系形成了鲜明的对比。

　　参数化类型的非转化特性不仅会体现在它们的构造函数上，也会同样体现在普通的函数上。比如，我们要定义用来描述上述类型值的函数 describe，那么对于以普通的复合类型 Jewelry 为首的类型族群来说，定义一个函数就足够了：

describe(jewelry::Jewelry) = "A $(typeof(jewelry))"

　　但对于以参数化的复合类型 Drawer 为首的类型族群而言，我们如果只定义下面这个函数：

describe(drawer::Drawer{Jewelry}) = "$(describe(drawer.content))"

　　那么就无法让类型为 Drawer{Necklace} 或 Drawer{Ring} 的参数值传进去。不过，这里有两种解决办法。第一种办法，指定参数化类型但不指定其类型参数：

describe(drawer::Drawer) = "$(describe(drawer.content))"

　　这就是在告诉 Julia，参数值只要是 Drawer 类型的，不论它的类型参数值是什么，全都符合这个函数的定义。这样做固然是可以的。但在很多时候，适用范围太广通常不是一件好事。

　　第二种办法是，指定参数化类型及其类型参数，但只约束后者的有效范围。例如：

describe(drawer::Drawer{<:Jewelry}) = "$(describe(drawer.content))"

　　我们把参数 drawer 的类型声明为了 Drawer{<:Jewelry}。注意，在 <: 的左侧并没有 T。在这种情况下，只要参数值的类型是 Drawer，且它的类型参数值是 Jewelry 的子类型，就符合这个 describe 函数的定义。如此一来，我们向该函数传入 Drawer{Necklace} 或 Drawer{Ring} 类型的参数值就都没有问题了。

　　第二种解决办法是更好的。因为为了程序的稳定性和运行效率，我们总是需要给予恰当的类型约束。

　　最后，顺便说一下，我们可以把 Drawer{<:Jewelry} 看做是对协变类型的模拟。而 <: 在这里可以被视为转化标注（variance annotation）。所谓的协变是指，同一个参数化类型的多个确定类型之间可以存在继承关系，并且这种继承关系完全取决于它们的类型参数值之间的继承关系。例如：

julia> Drawer{<:Necklace} <: Drawer{<:Jewelry},
 Drawer{<:Ring} <: Drawer{<:Jewelry}
(true, true)

julia> Drawer{Necklace} <: Drawer{<:Jewelry},
 Drawer{Ring} <: Drawer{<:Jewelry}
(true, true)

julia>

　　不过，再次强调一下，参数化类型本身具有的是非转化特性。我们虽然可以通过上述方式对协变类型进行模拟，但对此要持有谨慎的态度，并要关注运用的合理性。因为这在为我们提供便利的同时，还可能会让程序变得更加复杂。

　　 7.1.3 参数化抽象类型

　　参数化的抽象类型与参数化的复合类型有着很多的共同点。比如，参数化的抽象类型定义相当于声明了一个抽象类型的族群。又比如，参数化的抽象类型本身是它的所有确定类型的超类型。还比如，对于确定的参数化抽象类型，不会由于其参数值之间存在继承关系，就形成继承关系（即非转化特性）。

　　那么，参数化的抽象类型有什么特殊的功用吗？显然，与普通的抽象类型一样，参数化抽象类型可以帮助我们搭建自己的类型层次结构。并且，它还可以构建出更加丰富的类型体系。

　　如果我们有如下的类型定义：

# 代表储物空间的抽象类型。
abstract type StorageSpace{T} end

# 代表抽屉的类型。
mutable struct Drawer{T} <: StorageSpace{T}
    content::T
end

# 代表展柜的类型。
mutable struct Showcase{T<:Goods} <: StorageSpace{T}
    drawer1::Drawer{T}
    drawer2::Drawer{T}
end

　　那么，对于每一个 StorageSpace 类型的确定类型，都会有一个 Drawer 类型的确定类型和一个 Showcase 类型的确定类型与之相对应。并且，后两者总是前者的子类型。例如：

julia> Drawer{Jewelry} <: StorageSpace{Jewelry},
 Showcase{Jewelry} <: StorageSpace{Jewelry}
(true, true)

julia> Drawer{Necklace} <: StorageSpace{Necklace},
 Showcase{Necklace} <: StorageSpace{Necklace}
(true, true)

julia> Drawer{Ring} <: StorageSpace{Ring},
 Showcase{Ring} <: StorageSpace{Ring}
(true, true)

julia>

　　我们可以看到，这个类型体系是立体的，而不是平面的。更重要的是，如果我们定义更多的 StorageSpace 类型的子类型，那么这个体系的规模就将呈现指数级的增长。

　　与参数化的复合类型一样，我们也可以对参数化抽象类型的类型参数做出范围约束。不过，对于以超类型的身份出现在其他类型定义当中的参数化抽象类型，我们就不能这么做了。这是什么意思呢？举个例子，我们在前面是这样再次定义 Showcase 类型的：

mutable struct Showcase{T<:Goods} <: StorageSpace{T}
    drawer1::Drawer{T}
    drawer2::Drawer{T}
end

　　在这个定义当中，以超类型的身份出现的参数化抽象类型 StorageSpace 不能被写成 StorageSpace{T<:Goods} 或者 StorageSpace{<:Goods}。因为这不符合 Julia 的语法，会使它报错。即使这个参数化抽象类型本身声明的类型参数就是 {T<:Goods} 也是如此。这是合乎情理的，因为参数化类型一旦定义完成，我们就不能再去修改其类型参数的声明了。在这里，我们可以把它写成 StorageSpace{T}，也可以写成像 StorageSpace{Goods} 这样的确定类型。

　　你可能已经注意到了，我对 Showcase 类型的类型参数做了范围约束，其值必须是 Goods 的子类型。我在前面没有给出 Goods 类型的定义。它其实就是一个代表了商品的普通的抽象类型而已。

　　没错，我们可以在参数化类型的定义当中对其超类型的类型参数做出进一步的约束。不过，对于进一步约束的方向，Julia 并没有严格的规定。我们既可以收紧先前的约束，也可以放宽先前的约束。我又定义了如下类型：

# 代表玩具的类型。
abstract type Toy <: Goods end

# 代表毛绒玩具的类型。
struct StuffedToy <: Toy end

# 代表电动玩具的类型。
struct ElectricToy <: Toy end

# 代表玩具箱的抽象类型。
abstract type ToyBox{T<:Toy} <: StorageSpace{T} end

# 代表纸板箱的类型。
mutable struct Carton{T<:Goods} <: ToyBox{T}
    content::T
end

　　抽象类型 ToyBox 是 StorageSpace 类型的又一个子类型，并且它对后者的类型参数 T 做了进一步的范围约束，使它的值必须是 Toy 的子类型。类似的，复合类型 Carton 是 ToyBox 类型的子类型，同时它也对后者的类型参数做出了自己的约束。但是，Carton 对 T 的约束比 ToyBox 对 T 的约束更加宽松，因为 Goods 是 Toy 的超类型。这在 Julia 中是允许的。

　　即便如此，我依然建议你在做进一步约束时要收紧而不要放宽。这起码有 3 个好处：

这样做是对超类型的延续，而不是破坏。从类型层次设计的角度讲，子类型的适用范围总是应该比超类型的适用范围更小。或者说，超类型的应用场景起码应该涵盖子类型的应用场景。
这样做更容易使人理解。顺应当前的类型继承纹理，可以让代码的阅读者更快速地领会到类型定义者的意图。虽然 “在纸板箱里放置商品” 从逻辑上讲是没有问题的，但这会让人对 “Carton 继承 ToyBox” 产生疑惑。难道这样的纸板箱只是玩具箱的一种吗？这显然有些自相矛盾了。
这样做可以避免类型的使用者犯错。使用者一旦看到了当前类型的定义，就可以完全了解到关于其类型参数的约束。因为当前类型对其参数的约束是最严格的。否则，如果像前面那样，那么 Carton{Goods}(StuffedToy()) 就一定会使 Julia 报错。因为它不符合 ToyBox 对 T 的约束。

　　总之，虽然参数化的抽象类型可以构建出更加丰富的类型体系，但它对类型体系的设计者也提出了更高的要求。这关乎类型体系的质量和使用者的心智负担，值得我们仔细思考。

　　 7.1.4 参数化原语类型

　　我们也可以定义参数化的原语类型。不过，与前面两种参数化类型相比，参数化原语类型的意义就不太大了。

　　我们都知道，原语类型的结构仅仅是一个扁平的比特序列。在定义这种类型的时候，我们只需要指定其比特序列的长度，也就是其值需要占据的存储空间的大小。因此，即使我们在这种类型的名称后面添加了类型参数，也无法在它的定义体中引用这个参数。比如，Julia 预定义的原语类型 Ptr 是这样的：

# 32-bit system:
primitive type Ptr{T} 32 end

# 64-bit system:
primitive type Ptr{T} 64 end

　　在这种情况下，类型参数已经失去了泛化数据结构的作用，而仅能作为特定类型的一种标签。例如，Ptr{Char} 代表了可以指向字符值的那种指针的类型，而 Ptr{Int64} 则代表可以指向 Int64 类型值的那种指针的类型。

　　由于上述的特定类型都是 Ptr 类型的子类型，所以我们说原语类型依然可以因参数化而成为当下的类型族群之首。另外，参数化的原语类型依然具有非转化特性。