Julia 常用的数学运算
贡献者: xzllxls
本文授权转载自郝林的 《Julia 编程基础》。原文链接:第 5 章 数值与运算。
1. 5.5 常用的数学运算
Julia 中的一些操作符可以用于数学运算或位运算(也就是比特运算)。这样的操作符也可以被称为运算符。因此,我们就有了数学运算符和位运算符这两种说法。
5.5.1 数学运算符
可用于数学运算的运算符请见下表。
| 运算名称 | 运算符 | 示意表达式 | 用途 |
| 一元加 | + | +x | 求 $x$ 的原值 |
| 一元减 | - | -x | 求 $x$ 的相反数,相当于 $0-x$ |
| 平方根 | √ | √x | 求 $x$ 的平方根 |
| 二元加 | + | x + y | 求 $x$ 和 $y$ 的和 |
| 二元减 | - | x - y | 求 $x$ 与 $y$ 的差 |
| 乘 | * | x * y | 求 $x$ 和 $y$ 的积 |
| 除 | / | x / y | 求 $x$ 与 $y$ 的商 |
| 逆向除 | \ | x \ y | 相当于 $y / x$ |
| 整除 | ÷ | x÷y | 求 $x$ 与 $y$ 的商且只保留整数 |
| 求余运算 | \% | x\%y | 求 $x$ 除以 $y$ 后得到的余数 |
| 幂运算 | ^ | x^y | 求 $x$ 的 $y$ 次方 |
可以看到,Julia 中通用的数学运算符共有 9 个。其中,与 + 和 - 一样,√ 也是一个一元运算符。它的含义是求平方根。在 REPL 环境中,我们可以通过输入 \sqrt[Tab] 写出这个符号。我们还可以用函数调用 sqrt(x) 来替代表达式 √x。
所谓的一元运算是指,只有一个数值参与的运算,比如 √x。更宽泛地讲,根据参与操作的对象的数量,操作符可被划分为一元操作符(unary operator)、二元操作符(binary operator)或三元操作符(ternary operator)。其中,参与操作的对象又被称为操作数(operand)。
除上述的运算符之外,Julia 还有一个专用于 Bool 类型值的一元运算符 !,称为求反运算符。它会将 true 变为 false,反之亦然。
这些数学运算符都是完全符合数学逻辑的。所以我在这里就不再展示它们的示例了。
5.5.2 位运算符
我们都知道,任何值在底层都是根据某种规则以二进制的形式存储的。数值也不例外。我们把以二进制形式表示的数值简称为二进制数。所谓的位运算,就是针对二进制数中的比特(或者说位)进行的运算。这种运算可以逐个地控制数中每个比特的具体状态(0 或 1)。
Julia 中的位运算符共有 7 个。如下表所示。
| 运算名称 | 运算符 | 示意表达式 | 简要说明 |
| 按位求反 | ~ | ~$x$ | 求 $x$ 的反码,相当于每一个二进制位都变反 |
| 按位求与 | $\And$ | $x \And y$ | 逐个对比 $x$ 和 $y$ 的每一个二进制位,只要有 $0$ 就为 $0$,否则为 $1$ |
| 按位求或 | ` | ` | `$x$ |
| 按位异或 | ⊻ | $x$ ⊻ $y$ | 逐个对比 $x$ 和 $y$ 的每一个二进制位,只要不同就为 $1$,否则为 $0$ |
| 逻辑右移 | >>> | $x$ >>> $y$ | 把 $x$ 中的所有二进制位统一向右移动 $y$ 次,并在空出的位上补 $0$ |
| 算术右移 | >> | $x$ >> $y$ | 把 $x$ 中的所有二进制位统一向右移动 $y$ 次,并在空出的位上补原值的最高位 |
| 逻辑左移 | << | $x$ << $y$ | 把 $x$ 中的所有二进制位统一向左移动 $y$ 次,并在空出的位上补 $0$ |
利用 bitstring 函数,我们可以很直观地见到这些位运算符的作用。例如:
julia> x = Int8(-10)
-10
julia> bitstring(x)
"11110110"
julia> bitstring(~x)
"00001001"
julia>
可以看到,按位求反的运算符 ~ 会把 x 中的每一个比特的状态都变反(由 0 变成 1 或由 1 变成 0)。这也是 Julia 中唯一的一个只需一个操作数的位运算符。因此,它与前面的 + 和 - 一样,都可以被称为一元运算符。
我们再来看按位求与和按位求或:
julia> y = Int8(17)
17
julia> bitstring(x)
"11110110"
julia> bitstring(y)
"00010001"
julia> bitstring(x & y)
"00010000"
julia> bitstring(x | y)
"11110111"
julia>
我们定义变量 y,并由它来代表 Int8 类型的整数 17。y 的二进制表示是 00010001。对比变量 x 的二进制表示 11110110,它们只在左边数的第 4 位上都为 1。因此,x & y 的结果就是 00010000。另一方面,它们只在右数第 4 位上都为 0,所以 x | y 的结果就是 11110111。
按位异或的运算符 ⊻ 看起来很特别。因为在别的编程语言中没有这个操作符。在 REPL 环境中,我们可以通过输入 \xor[Tab] 或 \veebar[Tab] 写出这个符号。我们还可以用函数调用 xor(x, y) 来替代表达式 x ⊻ y。
我们在前表中也说明了,x ⊻ y 的含义就是逐个对比 x 和 y 的每一个二进制位,只要不同就为 1,否则为 0。示例如下:
julia> bitstring(x), bitstring(y), bitstring(x ⊻ y)
("11110110", "00010001", "11100111")
julia>
Julia 提供了 3 种位移运算,分别是逻辑右移、算术右移和逻辑左移。下面是演示代码:
julia> bitstring(x)
"11110110"
julia> bitstring(x >>> 3)
"00011110"
julia> bitstring(x >> 3)
"11111110"
julia> bitstring(x << 3)
"10110000"
julia>
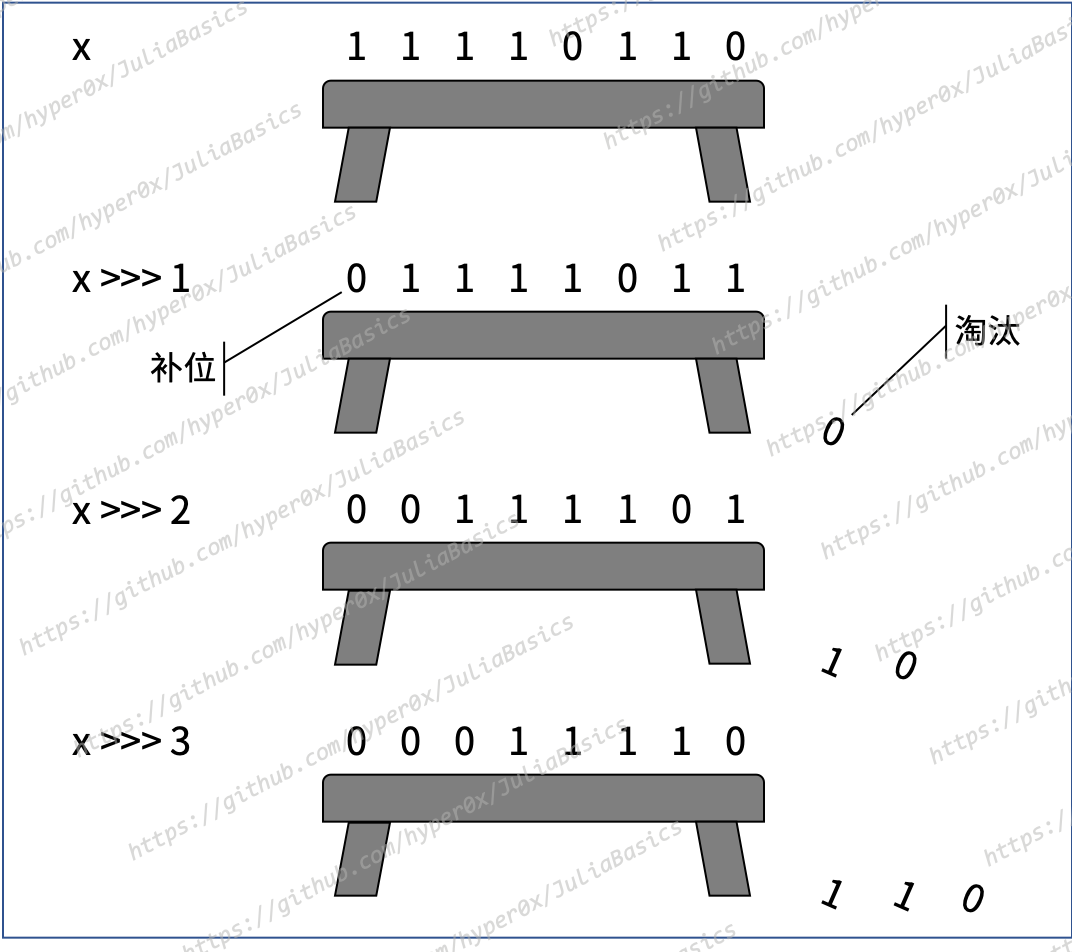
在位移运算的过程中,数值的宽度(或者说占用的比特数)是不变的。我们可以把承载一个数值的存储空间看成一条板凳,而数值的宽度就是这条板凳的宽度。现在,有一条板凳承载了 x 变量代表的那个整数,并且宽度是 8。也就是说,这条板凳上有 8 个位置,可以坐 8 个比特(假设比特是某种生物)。
每一次位移,板凳上的 8 个比特都会作为整体向左或向右移动一个位置。在移动完成后,总会有 1 个比特被挤出板凳而没有位置可坐,并且也总会有 1 个位置空出来。比如,如果向右位移一次,那么最右边的那个比特就会被挤出板凳,同时最左边会空出一个位置。没有位置可坐的比特会被淘汰,而空出来的位置还必须引进 1 个新的比特。
好了,我们现在来看从 11110110 到 00011110 的运算过程。后者是前者逻辑右移三次之后的结果。按照前面的描述,在向右移动三次之后,最右边的 3 个比特被淘汰了。因此,这时的二进制数就变为了 11110。又由于,逻辑右移运算会为所有的空位都填补 0(状态为 0 的比特),所以最终的二进制数就是 00011110。
与逻辑右移相比,算术右移只有一点不同,那就是:它在空位上填补的不是 0,而是原值的最高位。什么叫最高位?其实它指代的就是位置最高的那个比特。对于一个二进制数,最左边的那个位置就是最高位,而最右边的那个位置就是最低位。x 的值 11110110 的最高位是 1。因此,在算术右移三次之后,我们得到的新值就是 11111110。
与右移运算不同,左移运算只有一种。我们把它称为逻辑左移。这主要是因为该运算也会为空位填补 0。所以,11110110 经过逻辑左移三次之后就得到了 10110000。
5.5.3 运算同时赋值
Julia 中的每一个二元的数学运算符和位运算符都可以与赋值符号 = 联用,可称之为更新运算符。联用的含义是把运算的结果再赋给参与运算的变量。例如:
julia> x = 10; x %= 3
1
julia>
REPL 环境回显的 1 就是变量 x 的新值。但要注意,这种更新运算相当于把新的值与原有的变量进行绑定,所以原有变量的类型可能会因此发生改变。示例如下:
julia> x = 10; x /= 3
3.3333333333333335
julia> typeof(x)
Float64
julia>
显然,x 变量原有的类型肯定是某个整数类型(Int64 或 Int32)。但更新运算使它的值变成了一个 Float64 类型的浮点数。因此,该变量的类型也随之变为了 Float64。
所有的更新运算符罗列如下:
+= -= *= /= \= ÷= %= ^= &= |= ⊻= >>>= >>= <<=
前 8 个属于数学运算,后 6 个属于位运算。
5.5.4 数值的比较
理所应当,数值与数值之间是可以比较的。在 Julia 中,这种比较不但可以发生在同类型的值之间,还可以发生在不同类型的值之间,比如整数和浮点数。通常,比较的结果会是一个 Bool 类型的值。
对于整数之间的比较,我们就不多说了。它与数学中的标准定义没有什么两样。至于浮点数,相关操作仍然会遵循 IEEE 754 技术标准。这里存在 4 种互斥的比较关系,即:小于(less than)、等于(equal)、大于(greater than)和无序的(unordered)。
具体的浮点数比较规则如下:
- 只要参与比较的两个数值中有一个是 NaN,比较的结果就必然是
false。因为 NaN 不与任何东西相等,包括它自己。或者说,这种情况下的所有比较关系都是无序的。 - Inf 等于它自己,并且一定大于除了 NaN 之外的任何数。
- -Inf 等于它自己,并且一定小于除了 NaN 之外的任何数。
- 正零(0.0)和负零(-0.0)是相等的。尽管它们在底层存储上是不同的。
- 其他情况下的有限浮点数比较将会按照数学中的标准定义进行。
Julia 中标准的比较操作符如下表。
| 操作符 | 含义 |
| == | 等于 |
| != ≠ | 不等于 |
| < | 小于 |
| <= ≤ | 小于或等于 |
| > | 大于 |
| >= ≥ | 大于或等于 |
注意,对于不等于、小于或等于以及大于或等于,它们都有两个等价的操作符可用。表中已用空格将它们分隔开了。
这些比较操作符都可以用于链式比较,例如:
julia> 1 < 3 < 5 > 2
true
julia>
只有当链式比较中的各个二元比较的结果都为 true 时,链式比较的结果才会是 true。注意,我们不要揣测链中的比较顺序,因为 Julia 未对此做出任何定义。
在这些比较操作符当中,我们需要重点关注一下 == 我们之前使用过一个用于判断相等的操作符 ===。另外,还有一个名叫 isequal 的函数也可以用于判等。我们需要明确这三者之间的联系和区别。
首先,操作符 === 代表最深入的判等操作。我们在前面说过,对于可变的值,这个操作符会比较它们在内存中的存储地址。而对于不可变的值,该操作符会逐个比特地比较它们。
其次是操作符 ==。它完全符合数学中的判等定义。它只会比较数值本身,而不会在意数值的类型和底层存储方式。对于浮点数,这种判等操作会严格遵循 IEEE 754 技术标准。顺便说一句,在判断两个字符串是否相等时,它会逐个字符地进行比较,而忽略其底层编码。
函数 isequal 用于更加浅表的判等。在大多数情况下,它的行为都会依从于操作符 ==。在不涉及浮点数的时候,它会直接返回 == 的判断结果。那为什么说它更加浅表呢?这是因为,对于那些特殊的浮点数值,它只会去比较它们的字面含义。它同样会判断两个 Inf(或者两个 -Inf)是相等的,但也会判断两个 NaN 是相等的,还会判断 0.0 和 -0.0 是不相等的。这些显然并未完全遵从 IEEE 754 技术标准中的规定。下面是相应的示例:
julia> isequal(NaN, NaN)
true
julia> isequal(NaN, NaN16)
true
julia> isequal(Inf32, Inf16)
true
julia> isequal(-Inf, -Inf32)
true
julia> isequal(0.0, -0.0)
false
julia>
另外,=== 和 isequal 无论如何都会返回一个 Bool 类型的值作为结果。操作符 == 在绝大多数情况下也会如此。但当至少有一方的值是 missing 时,它就会返回 missing。missing 是一个常量,也是类型 Missing 的唯一实例。它用于表示当前值是缺失的。
下面的代码展示了上述 3 种判等操作在涉及 missing 时的判断结果:
julia> missing === missing
true
julia> missing === 0.0
false
julia> missing == missing
missing
julia> missing == 0.0
missing
julia> isequal(missing, missing)
true
julia> isequal(missing, 0.0)
false
julia>
最后,对于不同类型数值之间的比较,Julia 一般会贴合数学上的定义。比如:
julia> 0 == 0.0
true
julia> 1/3 == 1//3
false
julia> 1 == 1+0im
true
julia>
5.5.5 操作符的优先级
Julia 对各种操作符都设定了特定的优先级。另外,Julia 还规定了它们的结合性。操作符的优先级越高,它涉及的操作就会越提前进行。比如:对于运算表达式 10+3^2 来说,由于运算符 ^ 的优先级比作为二元运算符的 + 更高,所以幂运算 3^2 会先进行,然后才是求和运算。
操作符的结合性主要用于解决这样的问题:当一个表达式中存在且仅存在多个优先级相同的操作符时,操作的顺序应该是怎样的。一个操作符的结合性可能是,从左到右的、从右到左的或者未定义的。像我们在前面说的比较操作符的结合性就是未定义的。
下表展示了本章所述运算符的优先级和结合性。上方运算符的优先级会高于下方的运算符。
| 操作符 | 用途 | 结合性 |
+ - √ ~ ^ | 一元的数学运算和位运算,以及幂运算 | 从右到左的 |
<< >> >>> | 位移运算 | 从左到右的 |
* / \ ÷ \% $\And$ | 乘法、除法和按位与 | 从左到右的 |
+ - ⊻ | 加法、减法、按位或和按位异或 | |
== != < <= > >= === !== | 比较操作 | 未定义的 |
= += -= *= /= = ÷= \%= ^= == ⊻= >>>= >>= <<= | 赋值操作和更新运算 |
此外,数值字面量系数(如 -3x+1 中的 x)的优先级略低于那几个一元运算符。因此,表达式 -3x 会被解析为 (-3) * x,而表达式 √4x 则会被解析为 (√4) * x。可是,它与幂运算符的优先级却是相当的。所以,表达式 3^2x 和 2x^3 会被分别解析为 3^(2x) 和 2 * (x^3)。也就是说,它们之间会依照从右到左的顺序来结合。
对于运算表达式,我们理应更加注重正确性和(人类)可读性。因此,我们总是应该在复杂的表达式中使用圆括号来明确运算的顺序。比如,表达式 (2x)^3 的运算顺序就一定是先做乘法运算再做幂运算。不过,过多的括号有时也会降低可读性。所以我们往往需要对此做出权衡。如有必要,我们可以分别定义表达式的各个部分,然后再把它们组合在一起。