Julia 整数
贡献者: xzllxls
本文授权转载自郝林的 《Julia 编程基础》。原文链接:第 5 章 数值与运算。
1. 5.2 整数
我们在前面说过,整数类型又被分为有符号类型和无符号类型。后两者分别包含了 6 种和 5 种具体类型。我们为了表示这些类型的值而输入的内容又被称为整数字面量。比如,上一章示例中的 1、2、4、2020 都是整数字面量。
5.2.1 类型与取值
整数类型的名称大都很直观,并且它们的宽度也都已经体现在名称中了。详见下表。
| 类型名 | 是否有符号? | 其值占用的比特数 | 最小值 | 最大值 |
| Int8 | 是 | $8$ | $-2^7$ | $2^7 - 1$ |
| UInt8 | 否 | $8$ | $0$ | $2^8 - 1$ |
| Int16 | 是 | $16$ | $-2^{15}$ | $2^{15} - 1$ |
| UInt16 | 否 | $16$ | $0$ | $2^{16} - 1$ |
| Int32 | 是 | $32$ | $-2^{31}$ | $2^{31} - 1$ |
| UInt32 | 否 | $32$ | $0$ | $2^{32} - 1$ |
| Int64 | 是 | $64$ | $-2^{63}$ | $2^{63} - 1$ |
| UInt64 | 否 | $64$ | $0$ | $2^{64} - 1$ |
| Int128 | 是 | $128$ | $-2^{127}$ | $2^{127} - 1$ |
| UInt128 | 否 | $128$ | $0$ | $2^{128} - 1$ |
我们最好记住该表中各个类型的最小值和最大值。这并不困难,因为它们是有规律可循的。不过,实在记不住也没有关系。通过调用 typemin 函数和 typemax 函数,我们可以分别获得某一个整数类型能够表示的最小值和最大值,例如:
julia> typemin(Int8), typemax(Int8)
(-128, 127)
julia> typemin(UInt8), typemax(UInt8)
(0x00, 0xff)
julia>
严格来说,Bool 类型也属于整数类型。因为它与 Signed 和 Unsigned 一样,也是 Integer 类型的直接子类型。Bool 类型的宽度(也就是其值占用的比特数)是 8,最小值是 0(即 false),最大值是 1(即 true)。
此外,Julia 还定义了 Int 和 UInt。Int 代表了有符号整数的默认类型。在 32 位的计算机系统中,它们分别是 Int32 和 UInt32 的别名。而在 64 位的计算机系统中,它们分别是 Int64 和 UInt64 的别名。如此一来,我们在 REPL 环境中随便输入一个整数字面量,就能猜出它的类型:
julia> typeof(2020) # 在 32 位的计算机系统中
Int32
julia>
julia> typeof(2020) # 在 64 位的计算机系统中
Int64
julia>
这完全取决于我们的计算机系统的位数(或者说字宽)。顺便说一句,我们可以通过访问常量 Sys.WORD_SIZE 来获知自己的计算机系统的字宽。
不过,对于较大的整数,Julia 会自动使用宽度更大的整数类型,例如:
julia> typeof(1234567890123456789)
Int64
julia> typeof(12345678901234567890)
Int128
julia>
注意,在这个例子中,整数字面量的类型是否为 Int128,依据的不是字面量的长度,而是字面量表示的整数是否大于 Int64 类型的最大值。
5.2.2 表示方法
与前面的有符号整数不同,无符号整数会使用以 0x 为前缀的十六进制形式来表示。比如:
julia> UInt32(2020)
0x000007e4
julia> UInt64(2020)
0x00000000000007e4
julia>
我们都知道,在这些十六进制整数中,字母 a 到 f 分别代表了十进制整数 10 到 15,并且大写这些字母也是可以的。注意,无符号整数值的类型会由字面量本身决定:
julia> typeof(0x01)
UInt8
julia> typeof(0x001)
UInt16
julia> typeof(0x00001)
UInt32
julia> typeof(0x000000001)
UInt64
julia> typeof(0x00000000000000001)
UInt128
julia>
无符号整数值 0x01 只需占用 8 个比特(1 位的十六进制数相当于 4 位的二进制数),因此使用 UInt8 类型就足够了。无符号整数值 0x001 占用的比特是 12 个,超出了 UInt8 类型的位数,所以就需要使用 UInt16 类型。而 0x00001 的占位是 20 个,所以需要使用 UInt32 类型。以此类推。总之,一个无符号整数值的默认类型将会是能够容纳它的那个宽度最小的类型。
除了十六进制之外,我们还可以使用二进制或八进制的形式来表示无符号整数值。比如:
julia> 0b00000001
0x01
julia> 0o001
0x01
julia>
以`0b`为前缀的整数字面量就是以二进制形式表示的整数,而以 0o 为前缀的整数字面量则是以八进制形式表示的整数。在这里,数字 1 至少需要 8 位的二进制数或 3 位的八进制数或 2 位的十六进制数来表示。即使我们输入的位数不够也没有关系,Julia 会自动帮我们在高位补 0 以填满至相应类型的位数(这里是 8 个比特):
julia> 0b001
0x01
julia> 0o01
0x01
julia> 0x1
0x01
julia>
对于更大的无符号整数值的字面量来说也是类似的。
注意,二进制、八进制和十六进制的字面量可以表示无符号的整数值,但不能表示有符号的整数值。虽然我们可以在这些字面量的前面添加负号 -,但是它们表示的依然是无符号的整数值。例如:
julia> -0x01, typeof(-0x01), Int16(-0x01)
(0xff, UInt8, 255)
julia>
不要被字面量 -0x01 中的负号迷惑,它表示的值的类型仍然是 UInt8。0xff 实际上是负的 0x01(也就是 -1)的补码。但由于十六进制字面量表示的整数值只能是无符号的,所以 Julia 会把它视为一个无符号整数值的原码。如此一来,字面量 -0x01 代表的整数值就是 255。
顺便说一下,我们可以使用下划线 _ 作为数值字面量中的数字分隔符。至于划分的具体间隔,Julia 并没有做硬性的规定。例如:
julia> 2_020, 0x000_01, 0b000_000_01, -0x0_1
(2020, 0x00000001, 0x01, 0xff)
julia>
5.2.3 关于溢出
我们已知每个整数类型的最小值和最大值。当一个整数值超出了其类型的取值范围时,我们就说这个值溢出(overflow)了。
以 64 位的计算机系统为例,Julia 对整数值溢出有两种处理措施,具体如下:
- 对于其类型的宽度小于
64的整数值,值不变,其类型会被提升到Int64。 - 对于其类型的宽度等于或大于
64的整数值,其类型不变,对值采取环绕式(wraparound)处理。
也就是说,对于 Int8、Int16、Int32、UInt8、UInt16 和 UInt32 这 6 个类型,Julia 会把溢出值的类型自动地转换为 Int64。这样的话,这些值就不再是溢出的了。
对于宽度更大的整数类型,Julia 会采取不同的应对措施——环绕式(wraparound)处理。这是什么意思呢?比如,当一个 Int64 类型的整数值比这个类型的最大值还要大 1 的时候,该值就会变成这个类型的最小值。相对应的,当这个类型的整数值比其最小值还要小 1 的时候,该值就会变成这个类型的最大值。示例如下:
julia> int1 = typemax(Int64)
9223372036854775807
julia> int2 = int1 + 1
-9223372036854775808
julia> int2 == typemin(Int64)
true
julia> int3 = int2 - 1
9223372036854775807
julia> int3 == typemax(Int64)
true
julia>
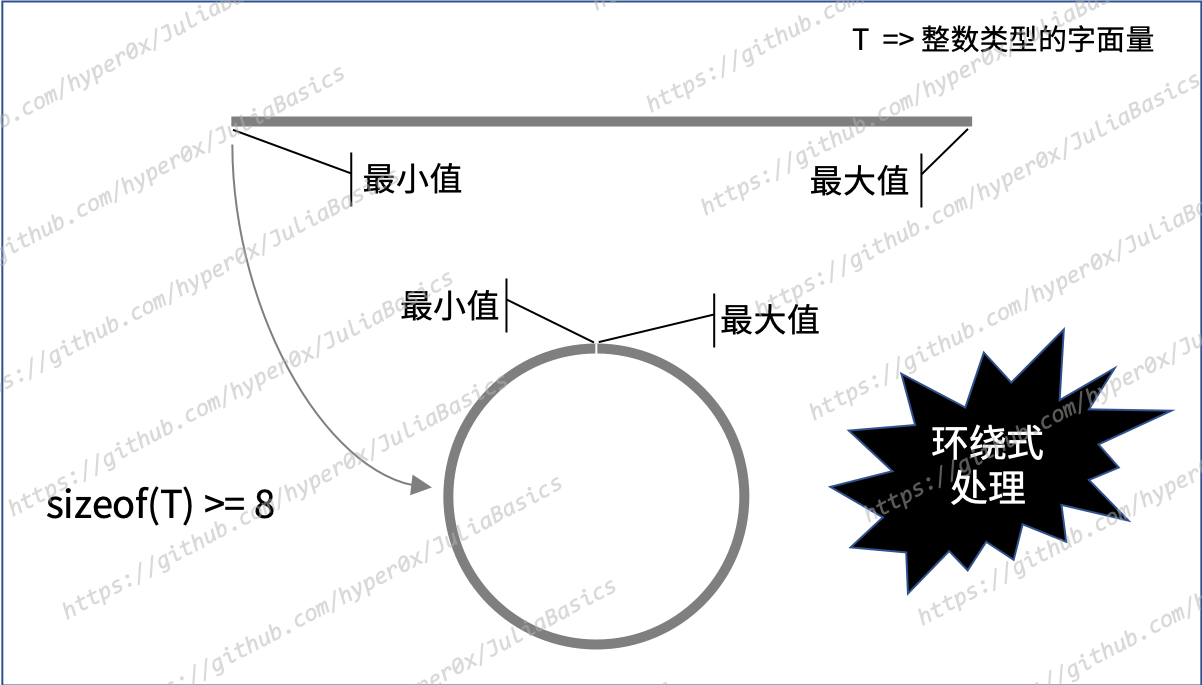
可以想象一下,对于一个宽度小于 64 的整数类型,它的所有可取值共同形成了一根又长又直的棍子。棍子上的值以由小到大的顺序从左到右排列。棍子的最左端是它的最小值,而最右端是它的最大值。
但对于像 Int64 这样的整数类型来说,其所有可取值共同形成的就不再是一根棍子了,而是一个圆环。这就好像把原来的棍子掰弯并首尾相接了一样。当该类型的值从它的最大值变更为最大值再加 1 时,就好似从圆环接缝的右侧移动一格,到了接缝左侧。相对应的,当该类型的值从它的最小值变更为最小值再减 1 时,就好像从圆环接缝的左侧移动一格,到了接缝右侧。这样的处理方式就叫做对整数溢出的环绕式处理。
总之,对于 Int64、Int128、UInt64 和 UInt128 这 4 个类型,Julia 会对溢出值做环绕式处理。
如果你需要的是不会溢出的整数类型,那么可以使用 BigInt。它的值的大小只受限于当前计算机的内存空间。
5.2.4 BigInt
BigInt 类型属于有符号的整数类型。它表示的数值可以是非常大的正整数,也可以是非常小的负整数。由此,我们可以说,它的值可以是任意精度的。
与其他的整数类型一样,其实例的构造函数与类型拥有相同的名称。并且,我们还可以使用一种非常规的字符串来构造它的值。例如:
julia> BigInt(1234567890123456789012345678901234567890)
1234567890123456789012345678901234567890
julia> typeof(ans)
BigInt
julia> big"1234567890123456789012345678901234567890"
1234567890123456789012345678901234567890
julia> typeof(ans)
BigInt
julia>
可以看到,我们把一串很长的数字传给了 BigInt 函数,并由此构造了一个 BigInt 类型的值。实际上,BigInt 函数接受的唯一参数可以是任意长度的整数字面量,也可以是任何其他整数类型的值。
甚至,这个构造函数的参数值还可以是像 big"1234" 这样的非常规字符串。不过,我们没有必要这么做。因为 big"1234" 本身就能够表示一个 BigInt 类型的实例。更宽泛地讲,在一个内容形似整数的字符串前添加 big 这 3 个字母就可以把它变成一个 BigInt 类型的值。
另外,任何溢出的整数值的类型都不会被自动地转换成 BigInt。如有需要,我们只能手动地进行类型转换。
最后,你需要了解的是,虽然 BigInt 直接继承自 Signed 类型,但它是一个比较特殊的整数类型。它被定义在了 Base.GMP 包中,而其他的整数类型的定义都在 Core 包中。GMP 指的是 GNU Multiple Precision Arithmetic Library,可以翻译为多精度算术库。Julia 中的 Base.GMP 包实际上只是对这个库的再次封装而已。虽然如此,这样一个类型的值却可以直接与其他类型的数值一起做数学运算。这主要得益于 Julia 中数值类型的层次结构,以及它的类型提升和转换机制。