介子（综述）

                     

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 在粒子物理学中，介子是强子亚原子粒子，由一个夸克和一个反夸克组成，通过强相互作用结合在一起。因为介子由夸克子组成，它们的物理尺寸[需要进一步解释]，特别是直径约为 1 飞米，[1] 约为质子或中子尺寸的 1.2 倍。所有介子都是不稳定的，寿命最长的只有百分之几微秒。带电介子衰变(有时通过中介粒子)形成电子和中微子。不带电荷的介子可能衰变为光子。这两种衰变都意味着色不再是反应产物的特性。

　　 在原子核之外，介子在自然界中只是由夸克组成的粒子(如宇宙射线(高能质子和中子)和普通物质之间高能碰撞的短暂产物。通常通过使回旋加速器中的质子、反质子或其他粒子发生碰撞来人工地产生介子。

　　 高能(更大质量)介子是在大爆炸中瞬间产生的，在自然界中几乎不会出现。但是为了理解构成重介子的更重类型夸克的性质，可以通过粒子加速器实验来有规律地产生这种重介子。

　　 介子是强子粒子家族的一部分，简单地定义为由偶数个夸克组成的粒子。强子家族的其他成员是重子:由奇数个价夸克(至少 3 个)组成的亚原子粒子，一些实验显示存在奇异介子，它们不是具有通常的两个夸克(一个夸克和一个反夸克)，而是具有 4 个或更多。

　　 因为夸克的自旋为 1/2，介子和重子之间夸克数的差异导致传统的双夸克介子是玻色子，而重子是费米子。

　　 每种介子都有一个对应的反粒子(反介子)，其中夸克被它们对应的反粒子所取代，反之亦然。例如，正 $\pi$ 介子($\pi^+$)由一个上夸克和一个下反夸克组成；它相应的反粒子负 $\pi$ 由一个上反夸克和一个下夸克组成。因为介子由夸克组成，所以它们同时参与弱相互作用和强相互作用。带净电荷的介子也参与电磁相互作用。介子根据它们的夸克含量、总角动量、奇偶性和其他各种性质，如碳奇偶性和重力奇偶性来分类。虽然没有介子是稳定的，但质量较低的介子比质量较大的介子更稳定，因此在粒子加速器或宇宙射线实验中更容易观察和研究。介子通常比重子质量小，这意味着它们在实验中更容易产生，因此比重子更容易表现出某些高能现象。例如，粲夸克于 1974 年首次出现在 J/Psi 介子(j/ψ), 1977 年在[2][3] 和 upsilon 介子(ϒ)中的底部夸克。[4]

1. 历史

　　 从理论上考虑，1934 年汤川秀树[5][6] 预测了 “介子” 作为将原子核结合在一起的核力的载体的存在和近似质量。如果没有核力，所有带有两个或更多质子的原子核都会因电磁排斥而分裂。汤川称他的载体粒子介子，来自μέσος介子，希腊语中 “中间体” 一词，因为它的预测质量介于电子质量和质子质量之间，质子质量约为电子质量的 1836 倍。汤川最初把他的粒子命名为 “介子”，但物理学家沃纳·海森堡(他的父亲是慕尼黑大学的希腊教授)纠正了他的说法。海森堡指出，希腊单词 “介子” 中没有 “tr”。[7]

　　 汤川介子的第一个候选者，现在在现代术语中被称为μ子，是 1936 年由卡尔·大卫·安德森和其他人在宇宙射线相互作用的衰变产物中发现的。μ介子有合适的质量成为汤川强核力的载体，但是在接下来的十年里，它显然不是合适的粒子。最终发现 “μ介子” 根本不参与强核相互作用，而是表现得像电子的重态，最终被归类为像电子一样的轻子，而不是介子。做出这一选择的物理学家决定，除了粒子质量之外，应该寻找其他属性来作为分类的依据。

　　 第二次世界大战(1939-1945)期间，亚原子粒子的研究出现了多年的延迟，大多数物理学家都在为战争需要而从事应用项目。1945 年 8 月战争结束时，许多物理学家逐渐回到和平时期的研究。第一个被发现的真正介子是后来被称为 “$\pi$ 介子”(或 $\pi$ 介子)。这个发现是塞西尔·鲍威尔、塞萨尔·拿铁和朱塞佩·奥契亚利尼在 1947 年发现的，他们在英国布里斯托尔大学根据安第斯山脉的摄影胶片研究宇宙射线产品。其中一些介子的质量与已知介子大致相同，但似乎是通过衰变得到的，这导致物理学家罗伯特·马尔夏克在 1947 年假设它实际上是一个新的不同的介子。在接下来的几年里，更多的实验表明π介子确实参与了强相互作用。$\pi$ 介子(作为虚拟粒子)也被认为是原子核中核力的主要载体。其他介子，如虚拟ρ介子也参与了这种力的调节，但程度较轻。发现π介子后，汤川因其预言获得了 1949 年诺贝尔物理学奖。

　　 在过去，介子这个词有时被用来指任何力的载体，比如 “Z0 介子”，它参与了弱相互作用的调解。[8] 然而，这种用途已经失宠，介子现在被定义为由成对的夸克和反夸克组成的粒子。

2. 概论

2.1 自旋、轨道角动量和总角动量

　　 自旋(量子数)是一个矢量，代表粒子的 “内在” 角动量。它的增量是 1/2 ħ.ħ经常被丢弃，因为它是自旋的 “基本” 单位，这意味着 “自旋 1” 意味着 “自旋 1 ħ".”(在一些自然单位系统中，ħ被选择为 1，因此不出现在方程中。)

　　 夸克是自旋为 1/2 的费米子。因为自旋投影增量为 1(即 1 ħ)，所以单个夸克具有长度为 1/2 的自旋矢量，并且具有两个自旋投影(SZ =+1/2 和 SZ = -1/2)。两个夸克可以使它们的自旋对齐，在这种情况下，两个自旋向量相加形成一个长度为 S = 1 的向量和三个自旋投影(Sz = +1，Sz = 0，Sz = -1)，称为自旋为 1 的三重态。如果两个夸克有不对齐的自旋，自旋向量加起来就是一个长度为 S = 0 的向量，只有一个自旋投影(Sz = 0)，称为自旋为 0 的单态。因为介子是由一个夸克和一个反夸克组成的，所以它们可以在三重态和单态中找到。

　　 还有另一个量子化的角动量，称为轨道角动量(量子数 l)，增量为 1 ħ，代表夸克围绕彼此旋转产生的角动量。因此，粒子的总角动量(量子数 J)是固有角动量(自旋)和轨道角动量的组合。它可以取从 J = | L-S |到 J = |L + S|的任何值，增量为 1。

表1：Meson angular momentum quantum numbers for L = 0, 1, 2, 3
S L J P (See below) $ J^P$
0 0 0 - $ 0^-$
0 1 1 + $1^+$
0 2 2 - $2^-$
0 3 3 + $3^+$
1 0 1s - 1−
1 1 2,1,0 + 2+, 1+, 0+
1 2 3, 2, 1 - 3−, 2−, 1−
1 3 4, 3, 2 + 4+, 3+, 2+

　　 粒子物理学家对没有轨道角动量(L = 0)的介子最感兴趣，因此研究最多的两组介子是 S = 1；L = 0，S = 0；L = 0，对应于 J = 1 和 J = 0，尽管它们不是唯一的。也可以从 S = 0 和 L = 1 获得 J = 1 粒子。如何区分 S = 1，L = 0 和 S = 0，L = 1 介子是介子光谱学研究的一个活跃领域。

2.2 宇称

　　 如果宇宙被反射到镜子里，大多数物理定律都是一样的——不管我们称之为 “左” 还是 “右”，事物都会以同样的方式运行。镜像反射的概念被称为宇称。无论宇宙是否在镜子中反射，重力、电磁力和强相互作用都以相同的方式表现，因此被称为宇称守恒(P 对称)。然而，弱交互确实区分了 “左” 和 “右”，这种现象被称为宇称破缺。

　　 基于此，人们可能会认为，如果每个粒子的波函数(更准确地说，每个粒子类型的量子场)同时镜像反转，那么新的波函数集将完全满足物理定律(除了弱相互作用)。事实证明，这并不完全正确:为了满足方程，某些类型粒子的波函数必须乘以-1，此外还要镜像反转。这种粒子类型被称为具有负或奇宇称(P = -1，或者可选地 P = -)，而其他粒子被称为具有正或偶宇称(P = +1，或者可选地 P = +)。

　　 对于介子，宇称与轨道角动量的关系是:[9]

\begin{equation} P=(-1)^{L+1}~ \end{equation}
其中 L 是波函数的相应球面调和的奇偶性的结果。“+ 1” 来自于这样一个事实，根据狄拉克方程，夸克和反夸克具有相反的固有同位旋。因此，介子的本征奇偶是夸克(+1)和反夸克(-1)的本征奇偶的乘积。由于这些不同，它们的乘积是-1，因此它贡献了指数中出现的 “+ 1”。因此，所有没有轨道角动量(L = 0)的介子都有奇宇称(P = -1)。

2.3 C-宇称

　　 C-宇称仅定义为自身为反粒子的介子(即中性介子)。它代表介子的波函数在夸克和反夸克交换下是否保持不变。[10] 如果

\begin{equation} \left\lvert q\bar q \right\rangle = \left\lvert \bar q q \right\rangle ~ \end{equation}
则介子是 “偶数”(C = +1)。另一方面，如果
\begin{equation} \left\lvert q\bar q \right\rangle =- \left\lvert \bar q q \right\rangle ~ \end{equation}
那么介子是 “奇数”(C = 1)。

　　 很少单独研究 C-宇称，更常见的是将 C-宇称与 P-宇称结合起来研究。CP-奇偶校验被认为是保守的，但后来发现在弱相互作用中被违反。[11][12]

2.4 G-宇称

　　 宇称是 C 宇称的推广。它不是简单地比较交换夸克和反夸克后的波函数，而是比较用介子交换相应的反介子后的波函数，而不管夸克的含量如何。[13]

　　 如果

\begin{equation} \left\lvert q_1\bar q_2 \right\rangle = \left\lvert \bar q_1q_2 \right\rangle ~ \end{equation}
则介子是 “偶数”(G = +1)。另一方面，如果
\begin{equation} \left\lvert q_1\bar q_2 \right\rangle =- \left\lvert \bar q_1q_2 \right\rangle ~ \end{equation}
那么介子是 “奇数”(G = 1)。

2.5 同位旋和电荷

　　 同位旋的概念是由维尔纳·海森堡(Werner Heisenberg)在 1932 年首次提出的，它用来解释质子和中子在强相互作用下的相似性。[14] 尽管它们有不同的电荷，但它们的质量非常相似，物理学家认为它们实际上是相同的粒子。不同的电荷被解释为某种类似自旋的未知激发的结果。这种未知的激发后来在 1937 年被尤金·维格纳称为同位旋。[15]当第一批介子被发现时，它们也是在研究同位旋时被发现的，三个π介子被认为是相同但是处于不同的同位旋状态的粒子

图
图 1：一个 u、d 或 s 夸克与一个 u、d 或 s 反夸克在 JP = 0− 构型中形成一个九重态（nonet）.
图
图 2：一个 u、d 或 s 夸克与一个 u、d 或 s 反夸克在 JP = 1− 构型中也形成一个九重态。

　　 同位旋的数学是以自旋的数学为模型的。同位旋投影以 1 的增量变化，就像自旋一样，每个投影都有一个 “带电状态”。因为 “$\pi$ 介子粒子” 有三种 “带电状态”，所以据说它的同位旋ⅰ= 1。它的 “带电状态” $\pi^+$, $\pi^0$，和 π−分别对应于同位旋投影 I3 = +1、I3 = 0 和 I3 = -1。另一个例子是 “ρ粒子”，也有三种带电状态。它的 “带电状态” ρ+, ρ0，和 ρ−分别对应于同位旋投影 $i_3$ = +1，$i_3$= 0，和 $i_3$ = -1。后来人们注意到同位旋投影通过下面这种关系与粒子的上夸克和下夸克组成有关：

\begin{equation} I_3=\frac{1}{2}[(n_u-n_{\bar u})-(n_d-n_{\bar d})]~ \end{equation}
其中 n 是上下夸克和反夸克的数量。

　　 在 “同位旋图” 中，三个 $\pi$ 和三个ρ被认为是两个粒子的不同状态。然而，在夸克模型中，ρ是 $\pi$ 介子的激发态。同位旋虽然传达了不准确的事物图像，但仍然被用来对强子进行分类，导致不自然且经常令人困惑的命名。因为介子是强子，所以也使用同位旋分类，上夸克和下夸克用 $ i_3$ =$+\frac{1}{2}$，上夸克和下夸克用 $ i_3$ =$-\frac{1}{2}$ 。

2.6 味道量子数

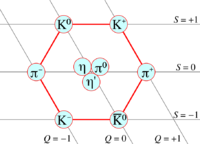
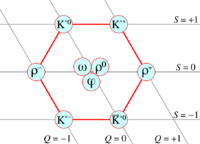
　　 异量子数 S(不要与自旋混淆)随着粒子质量上下波动。质量越高，奇异性越低(s 夸克越多)。粒子可以用同位旋投影(与电荷相关)和奇异性(质量)来描述(见 uds nonet 图)。当其他夸克被发现时，新的量子数被制成具有类似 udc 和 udb nonets 的描述。因为只有 u 和 d 质量是相似的，这种用同位旋和味道量子数来描述粒子质量和电荷的方法只适用于由一个 u、一个 d 和另一个夸克组成的导子，而对其他导子(例如 ucb 导子)来说则是无效的。如果夸克都有相同的质量，它们的行为将被称为对称，因为它们在强相互作用中的行为完全相同。然而，由于夸克质量不同，它们的相互作用方式也不同(就像放在电场中的电子因质量较轻而加速的速度比放在同一个电场中的质子快)，这种对称性被打破了。

　　 根据盖勒-曼-西岛公式，电荷(Q)与同位旋投影($i_3$)，重子数(B)和味道量子数(S, C, B′, T)由盖勒-曼-西岛公式:[17]

\begin{equation} Q=I_3+\frac{1}{2}(B+S+C+B'+T)~ \end{equation}
其中，S、C、B′和 T 分别代表奇异数、粲数、底和顶味道量子数。它们与奇异、粲、底和顶夸克与反夸克的数量有关，根据这种关系:
\begin{equation} S=-(n_s-n_{\bar s}) ~ \end{equation}
\begin{equation} C=+(n_c-n_{\bar c})~ \end{equation}
\begin{equation} B'=-(n_b-n_{\bar b})~ \end{equation}
\begin{equation} T=+(n_t-n_{\bar t})~ \end{equation}
这意味着盖勒-曼-西岛公式相当于夸克含量的电荷表达式:
\begin{equation} Q=\frac{2}{3}[(n_u-n_{\bar u})+(n_c-n_{\bar c})+(n_t-n_{\bar t})]-\frac{1}{3}[(n_d-n_{\bar d})+(n_s-n_{\bar s})+(n_b-n_{\bar b})]~ \end{equation}

3. 分类

　　 介子根据它们的同位旋(ⅰ)、总角动量(J)、宇称(P)、适用时的重力宇称(G)或重力宇称(C)以及夸克(q)含量分类。分类规则由粒子数据组定义，相当复杂。[18] 为了简单起见，这些规则以表格的形式呈现在下面。

3.1 介子的类型

　　 介子根据它们的自旋构型被分成几类。一些特定的构型根据它们自旋构型的数学性质被赋予特殊的名称。

表2：介子类型 [19]
类型 S L P J $J^P$
赝标量介子 0 0 - 0 $ 0^-$
赝标量介子 0,1 1 + 1 $ 1^+$
矢量介子 1 0,2 - 1 $ 1^-$
标量介子 11 + 0 $ 0^+$
张量介子 1 1,3 + 2 $2^+$

3.2 命名法

　　 无味介子

　　 无味介子是由一对相同味道的夸克和反夸克组成的介子(它们所有的味道量子数都为零:S= 0，C= 0，B′= 0，T= 0)。[20] 无味介子的规则是:[18]

表3：无味介子的命名
qq content $J^{P'C}\to I \downarrow$ $0^{-+} ,2^{-+}, 4^{-+} $... $1^{+-} ,3^{+-}, 5^{+-} $... $1^{--} ,2^{--}, 3^{--} $... $0^{++} ,1^{++}, 2^{++} $...
ud$\frac{u\bar u-d\bar d}{\sqrt{2}}$du 1 $\pi ^+ ,\pi ^0 ,\pi^-||b^+,b^0,b^-||\rho^+,\rho^0,\rho^-||a^+,a^0,a^-$
Mix of uu, dd, ss 0 $\eta ,\eta'||h,\eta'|| \omega,\varphi||f,f'$
cc 0 $\eta_c||h_c||\psi||\chi_c$
bb 0 $\eta_b||h_b||\gamma||\chi_b$
tt 0 $\eta_t||h_t||\theta||\chi_t$

　　 ^ C-宇称只与中性介子相关。

　　 ^对于 $J^{PC}$=$1^{--}$，ψ称为 $J/\psi$,此外

　　 味道介子

　　 味道介子是由一对不同味道的夸克和反夸克组成的介子。在这种情况下，规则更简单:主要符号取决于较重的夸克，上标取决于电荷，下标(如果有的话)取决于较轻的夸克。在表格形式中，它们是:[18]

表4：味道介子的命名
反夸克 $\to$ 夸克 上 下 粲 奇异 顶 底
上 - [20] $ D^0 || K^+ || T^0 || B^+$
下 [20] - $D^- || K^0 || T^- || B^0 $
粲$ D^0 || D^+ || - || D^+_s || T^0_c || B^+_c $
奇异 $K^- || K^0 || D^-_s || - || T^-_s || B^0_s $
顶 $T^0 || T^+ || T^0_c || T^+_s || - ||T^+_b $
底 $B^- || B^0 || B^-_c || B^0_s || T^-_b || -$

　　 此外：

4. 奇异介子

　　 奇异介子

　　 有实验证据表明粒子是强子(即由夸克组成)并且颜色中性，重子数为零，因此根据传统定义是介子。然而，这些粒子并不像上面讨论的所有其他传统介子那样由单个夸克/反夸克对组成。这些粒子的暂定类别是奇异介子。

　　 至少有五种奇异介子共振被两个或更多独立的实验证实存在。其中最具统计意义的是 Z(4430)，2007 年由贝尔实验发现，2014 年由 LHCb 证实。它含有四夸克:由两个夸克和两个反夸克组成的粒子。[21] 请参阅上面的主要文章，了解其他粒子共振是奇异介子的候选。

5. 列表

5.1 Pseudoscalar mesons

表5：Pseudoscalar mesons
Particl e name Particl e symbol Antipar ticle symbol Quark content Rest mass (MeV/$c^2$) $I^G$ $J^{PC}$ S C B' Mean lifetime (s) Commonly decays to (>5\% of decays)
Pion[22] $\pi^+$ $\pi^-$ u d 139.57018±0.00035 $1^-$ $ 0^- $ 0 0 0 (2.6033±0.0005)×10−8 $\mu^++v_\mu$
Pion[23] $\pi^0$ Self $\frac{u\bar u-d \bar d}{\sqrt{2}}$ 0134.9766±0.0006 $0^{-+}$ 1 0 0 0 (8.4±0.6)×10−17 $\gamma+\gamma$
Eta meson[24] $\eta $ Self $\frac{u\bar u+d\bar d-2s\bar s}{\sqrt{6}}$ 547.853±0.024 $0^+$ $0^{-+}$ 0 0 0 (5.0±0.3)×10−19 $\gamma+\gamma \quad or quad \pi^0+\pi^0+\pi^0 quad or quad \pi^++\pi^0+\pi^-$
Eta prime meson[25] $\eta'$ (958) Self $\frac{u\bar u+d\bar d+s\bar s}{\sqrt{3}}$ 957.66±0.24 $0^+$ $0^{-+}$ 0 0 0 (3.2±0.2)×10−21 $\pi^+ +\pi^-+\eta \quad or \quad (\rho^0+\gamma)/(\pi^+ +\pi^- +\gamma)\quad or \quad \pi^0+\pi^0+\eta$
Charmed eta meson[26] $\eta_c(1S)$Self cc 2980.3±1.2 $0^+$ $0^{-+}$ 0 0 0 (2.5±0.3)×10−23 See $\eta_C$ decay modes
Bottom eta meson[27] $\eta_b(1S)$ Self bb 9300±40 $0^+$ $ 0^{-+}$ 0 0 0 Unknown See $\eta_B$ decay modes
Kaon[28] $K^+$ $K^-$ us 493.677±0.016 $\frac{1}{2}$ $0^-$ 1 0 0 (1.2380±0.0021)×10−8 $\mu^+ +v_\mu \quad or \quad \pi^+ \pi^0 \quad or \quad \pi^0+e^+ +v_e \quad or \quad \pi^+ +\pi^0$
Kaon[29] $K^0$ $K^0$ ds 497.614±0.024 $\frac{1}{2}$ $0^-$ 1 0 0
K-Short[30] $K^0_L$ Self $\frac{d\bar s+s\bar d}{\sqrt{2}}$ 497.614±0.024 $\frac{1}{2}$ $0^-$ (*) 0 0 (8.953±0.005)×10−11 $\pi^+ +\pi^- \quad or \quad \pi^0+\pi^0$
K-Long[31] $K^0_L$ Self $ \frac{d\bar s+s\bar d}{\sqrt{2}}$ 497.614±0.024 $\frac{1}{2}$ $0^-$ (*) 0 0 (5.116±0.020)×10−8 $\pi^{\pm}+e^{\mp}+v_e \quad or \quad \pi^\pm+\mu^\mp+v_\mu\ \quad or \quad \pi^0+\pi^0+\pi^0 \quad or \quad \pi^+ +\pi^0+\pi^-$
D meson[32] $D^+$ $D^-$ $cd$ 1869.62±0.20 $\frac{1}{2}$ $0^-$ 0 +1 0 (1.040±0.007)×10−12See $D^+$ decay modes
D meson[33] $D^0$ $D^0$ cu 1864.84±0.17 $\frac{1}{2}$ $0^-$ 0 +1 0 (4.101±0.015)×10−13 See $D^0$ decay modes
strange D meson[34] $D^+_s$ $D^+_s$ cs 1968.49±0.34 0 $0^-$ +1 +1 0 (5.00±0.07)×10−13 See $D^+_s$ decay modes
B meson[35] $B^+$ $B^-$ ub 5279.15±0.31 $\frac{1}{2}$ $0^-$ 0 0 +1 (1.638±0.011)×10−12 See $B^+$ decay modes
B meson[36] $B^0$ $B^0$ db 5279.53±33 $\frac{1}{2}$ $0^-$ 0 0 +1 (1.530±0.009)×10−12 See $B^0$ decay modes
Strange B meson[37] $B^0_s$ $B^0_s$ sb 5366.3±0.6 0 $0^-$ -1 0 +1 1.470+0.026−0.027×10−12 See$ B^0_s$ decay modes
Charmed B meson[38] $B^+_c$ $B^+_c$ cb 6276±4 0 $0^-$ 0 +1 +1 (4.6±0.7)×10−13 See $B^+_c$ decay modes

　　 [a] Makeup inexact due to non-zero quark masses.

　　 [b] PDG reports the resonance width (Γ). Here the conversion τ = ħ⁄Γ is given instead.

　　 [c] Strong eigenstate. No definite lifetime (see kaon notes below)

　　 [d] The mass of the K0L and K0S are given as that of the K0. However, it is known that a difference between the masses of the K0L and K0S on the order of 2.2×10−11 MeV/c2 exists.[31]

　　 [e] Weak eigenstate. Makeup is missing small CP–violating term (see notes on neutral kaons below).

5.2 Vector mesons

表6：Vector mesons
Particle name Particle symbol Antiparticle symbol Quark content Rest mass (MeV/$c^2$) $I^G$ $J^{PC}$S C $B'$ Mean lifetime (s) Commonly decays to (>5\% of decays)
Charged rho meson[39] $\rho^+(770)$ $\rho^-(770)$ u d 775.4±0.4 $1^+$ 1^- 0 0 0 ~$4.5$x$10^{-24}$ $\pi^\pm+\pi^0$
Neutral rho meson[39] $\rho^0(770)$ Self $\frac{u\bar u-d\bar d}{\sqrt{2}}$ 775.49±0.34 $1^+$ $1^{--}$ 0 0 0 ~$4.5$x$10^{-24}$ $\pi^+ +\pi^-$
Omega meson[40] $\omega(782)$Self $\frac{u\bar u-d\bar d}{\sqrt{2}}$ 782.65±0.12 $0^-$ $1^{--}$ 0 0 0 (7.75±0.07)x$10^-{23}$ $\pi^+ +\pi^0 +\pi^- \quad$ or$\quad \pi^0+$ γ
Phi meson[41] $\varphi(1020)$ Self ss 1019.445±0.020 $0^-$ $1^{--}$ 0 0 0 $(1.55\text{±}0.01)$×$10^-22$ $K^+ +K^- \quad$or $\quad K^0_s + K^0_L \quad$or $\quad (\rho +\pi)/(\pi^+\pi^0 +\pi^-)$
J/Psi[42] $J/\Psi$ Self c c 3096.916±0.011 $0^-$ $1^{--}$ 0 0 0 ($7.1$±$0.2$)×$10^-21$ See $J/\Psi$ decay modes
Upsilon meson[43] ϒ (1S) Self b b 9460.30±0.26 $0^-$ $1^{--}$ 0 0 0 ($1.22$±$0.03$)×$10^-20$ See ϒ(1S) decay modes
Kaon[44] $K^{*+}$ $K^{*-}$ us 891.66±0.026 $\frac{1}{2}$ $1^-$ 1 0 0 ~$7.35$×$10^-20$ See $K^*$ (892) decay modes
Kaon[44] $K^{*0}$ $K^{*0}$ ds 896.00±0.025 $\frac{1}{2}$ $1^-$ 1 0 0 ($7.346$±$0.002$)×$10^-20$ See $K^*$ (892) decay modes
D meson[45] $D^{*+}(2010)$ $D^{*-}(2010)$ cd 2010.27±0.17 $\frac{1}{2}$ $1^-$ 0 +1 0 ($6.9$±$1.9$)×$10^-21$ $D^0+\pi^+ \quad$or $\quad D^+ +\pi^0$
D meson[46] $D^{*+}(2007)$ $D^{*+}(2007)$ cu 2006.97±0.19 $\frac{1}{2}$ $1^-$ 0 +1 0 >$3.1$×$10^-20$ $D^0+\pi^0 \quad$or $D^0+$ϒ
strange D meson[47] $D^{*+}_s$ $D^{*-}_s$ cs 2112.3±0.5 0 $1^-$ +1 *+1 0 >$3.4$×$10^-22$ $D^{*+}+\text{ϒ} \quad$or $\quad D^{*+}+\pi^0$
B meson[48] $B^{*+}$ $B^{*-}$ ub 5325.1±0.5 $\frac{1}{2}$ $1^-$ 0 0 +1 Unknown $B^+ +$ϒ
B meson[48] $B^{*0}$ $B^{*0}$ db 5325.1±0.5 $ \frac{1}{2}$$1^-$ 0 0 +1 Unknown $B^0 +$ϒ
Strange B meson[49] $B^{*0}_s$ $B^{*0}_s$ sb5412.8±1.3 0 $1^-$ -1 0 +1 Unknown $B^0_s+$ϒ
Charmed B meson† $B^{*+}_s$ $B^{*-}_s$ cb Unknown 0 $1^-$ 0 +1 +1 Unknown Unknown

　　 [f] PDG reports the resonance width (Γ). Here the conversion τ = ħ⁄Γ is given instead.

　　 [g] The exact value depends on the method used. See the given reference for detail.

5.3 Notes on neutral kaons

　　 There are two complications with neutral kaons:[50]

　　 Note that these issues also exist in principle for other neutral flavored mesons; however, the weak eigenstates are considered separate particles only for kaons because of their dramatically different lifetimes.[50]

6. 笔记

  1. D. Griffiths (2008)
  2. J.J. Aubert et al. (1974)
  3. J.E. Augustin et al. (1974)
  4. S.W. Herb et al. (1977)
  5. "Nobel Prize in Physics 1949". Presentation Speech. The Noble Foundation. 1949.
  6. H. Yukawa, (1935)
  7. G. Gamow, (1961)
  8. J. Steinberger, (1998)
  9. C. Amsler et al. (2008): Quark Model
  10. M.S. Sozzi (2008b)
  11. J.W. Cronin (1980)
  12. V.L. Fitch (1980)
  13. M.S. Sozzi (2008c)
  14. K. Gottfried, V.F. Weisskopf (1986)
  15. W. Heisenberg (1932)
  16. E. Wigner (1937)
  17. M. Gell-Mann (1964)
  18. S.S.M Wong (1998)
  19. C. Amsler et al. (2008): Naming scheme for hadrons
  20. W.E. Burcham, M. Jobes (1995)
  21. For the purpose of nomenclature, the isospin projection I3 isn't considered a flavour quantum number. This means that the charged pion-like mesons ($\pi^\pm$,$a^\pm$,$a^\pm$, and $\rho^\pm$ mesons) follow the rules of flavourless mesons, even if they aren't truly "flavourless".
  22. LHCb collaborators (2014): Observation of the resonant character of the Z(4430)− state
  23. C. Amsler et al. (2008): Particle listings – $\pi^\pm$
  24. C. Amsler et al. (2008): Particle listings – $\pi^0$
  25. C. Amsler et al. (2008): Particle listings – $\eta$
  26. C. Amsler et al. (2008): Particle listings – $\eta'$
  27. C. Amsler et al. (2008): Particle listings – $\eta_c$
  28. C. Amsler et al. (2008): Particle listings – $\eta_b$
  29. C. Amsler et al. (2008): Particle listings – $K^\pm$
  30. C. Amsler et al. (2008): Particle listings – $K^0$
  31. C. Amsler et al. (2008): Particle listings – $K^0_S$
  32. C. Amsler et al. (2008): Particle listings – $K^0_L$
  33. C. Amsler et al. (2008): Particle listings – $D^\pm$
  34. C. Amsler et al. (2008): Particle listings – $D^0$
  35. C. Amsler et al. (2008): Particle listings – $D^\pm_s$
  36. C. Amsler et al. (2008): Particle listings – $B^\pm$
  37. C. Amsler et al. (2008): Particle listings – $B^0$
  38. C. Amsler et al. (2008): Particle listings – B0s
  39. C. Amsler et al. (2008): Particle listings – $B^\pm_c$
  40. C. Amsler et al. (2008): Particle listings – $\rho$
  41. C. Amsler et al. (2008): Particle listings – $\omega(782)$
  42. C. Amsler et al. (2008): Particle listings – $\varphi$
  43. C. Amsler et al. (2008): Particle listings – $J/\Psi$
  44. C. Amsler et al. (2008): Particle listings – ϒ(1S)
  45. C. Amsler et al. (2008): Particle listings – $K^*$(892)
  46. C. Amsler et al. (2008): Particle listings – $D^{*\pm}$(2010)
  47. C. Amsler et al. (2008): Particle listings –$D^{*0}$(2007)
  48. C. Amsler et al. (2008): Particle listings – $D^{*\pm}_s$
  49. C. Amsler et al. (2008): Particle listings – $B^*$
  50. C. Amsler et al. (2008): Particle listings – $B^*_s$

7. 参考文献

　　 [1]D. Griffiths (2008).

　　 [2]J.J. Aubert et al. (1974).

　　 [3]J.E. Augustin et al. (1974).

　　 [4]S.W. Herb et al. (1977).

　　 [5]"Nobel Prize in Physics 1949". Presentation Speech. The Noble Foundation. 1949..

　　 [6]H. Yukawa, (1935).

　　 [7]G. Gamow, (1961).

　　 [8]J. Steinberger, (1998).

　　 [9]C. Amsler et al. (2008): Quark Model.

　　 [10]M.S. Sozzi (2008b).

　　 [11]V.L. Fitch (1980).

　　 [12]M.S. Sozzi (2008c).

　　 [13]K. Gottfried, V.F. Weisskopf (1986).

　　 [14]W. Heisenberg (1932).

　　 [15]E. Wigner (1937).

　　 [16]M. Gell-Mann (1964).

　　 [17]S.S.M Wong (1998).

　　 [18]C. Amsler et al. (2008): Naming scheme for hadrons.

　　 [19]W.E. Burcham, M. Jobes (1995).

　　 [20]For the purpose of nomenclature, the isospin projection I3 isn't considered a flavour quantum number. This means that the charged pion-like mesons (π±, a±, b±, and ρ± mesons) follow the rules of flavourless mesons, even if they aren't truly "flavourless"..

　　 [21]LHCb collaborators (2014): Observation of the resonant character of the Z(4430)− state.

　　 [22]C. Amsler et al. (2008): Particle listings – π±.

　　 [23]C. Amsler et al. (2008): Particle listings – π0

　　 [24]C. Amsler et al. (2008): Particle listings – η.

　　 [25]C. Amsler et al. (2008): Particle listings – η′.

　　 [26]C. Amsler et al. (2008): Particle listings – ηc.

　　 [27]C. Amsler et al. (2008): Particle listings – ηb.

　　 [28]C. Amsler et al. (2008): Particle listings – K±.

　　 [29]C. Amsler et al. (2008): Particle listings – K0.

　　 [30]C. Amsler et al. (2008): Particle listings – K0S.

　　 [31]C. Amsler et al. (2008): Particle listings – K0L.

　　 [32]C. Amsler et al. (2008): Particle listings – D±.

　　 [33]C. Amsler et al. (2008): Particle listings – D0.

　　 [34]C. Amsler et al. (2008): Particle listings – D±s.

　　 [35]C. Amsler et al. (2008): Particle listings – B±.

　　 [36]C. Amsler et al. (2008): Particle listings – B0.

　　 [37]C. Amsler et al. (2008): Particle listings – B0s.

　　 [38]C. Amsler et al. (2008): Particle listings – B±c.

　　 [39]C. Amsler et al. (2008): Particle listings – ρ.

　　 [40]C. Amsler et al. (2008): Particle listings – ω(782).

　　 [41]C. Amsler et al. (2008): Particle listings – φ.

　　 [42]C. Amsler et al. (2008): Particle listings – J/Ψ.

　　 [43]C. Amsler et al. (2008): Particle listings – ϒ(1S).

　　 [44]C. Amsler et al. (2008): Particle listings – K∗(892).

　　 [45]C. Amsler et al. (2008): Particle listings – D∗±(2010).

　　 [46]C. Amsler et al. (2008): Particle listings – D∗0(2007).

　　 [47]C. Amsler et al. (2008): Particle listings – D∗±s.

　　 [48]C. Amsler et al. (2008): Particle listings – B∗.

　　 [49]C. Amsler et al. (2008): Particle listings – B∗s.

　　 [50]J.W. Cronin (1980).

                     

© 小时科技 保留一切权利