经典力学（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：显示卫星绕地球轨道运动的示意图，其中展示了垂直的速度和加速度（力）矢量，通过经典力学的解释进行表示。

　　 经典力学是一种物理理论，用于描述物体的运动，例如抛射物、机械部件、航天器、行星、恒星和星系等。经典力学的发展涉及物理学方法和哲学的重大变革。[1] “经典” 这一限定词将这种力学类型与 20 世纪初物理学革命之后发展起来的物理学区分开来，这些现代物理理论揭示了经典力学的局限性。[2]

　　 经典力学最早的形式通常被称为牛顿力学。它基于 17 世纪以艾萨克·牛顿爵士为代表的奠基性工作的物理概念，以及牛顿、戈特弗里德·威廉·莱布尼茨、莱昂哈德·欧拉等人发明的数学方法，用来描述物体在力的作用下的运动。后来，基于能量的方法由欧拉、约瑟夫-路易·拉格朗日、威廉·罗恩·哈密顿等人发展，最终形成了分析力学（包括拉格朗日力学和哈密顿力学）。这些进步主要发生在 18 世纪和 19 世纪，超越了早期的工作；经过一定的修正，它们被应用于现代物理学的各个领域。

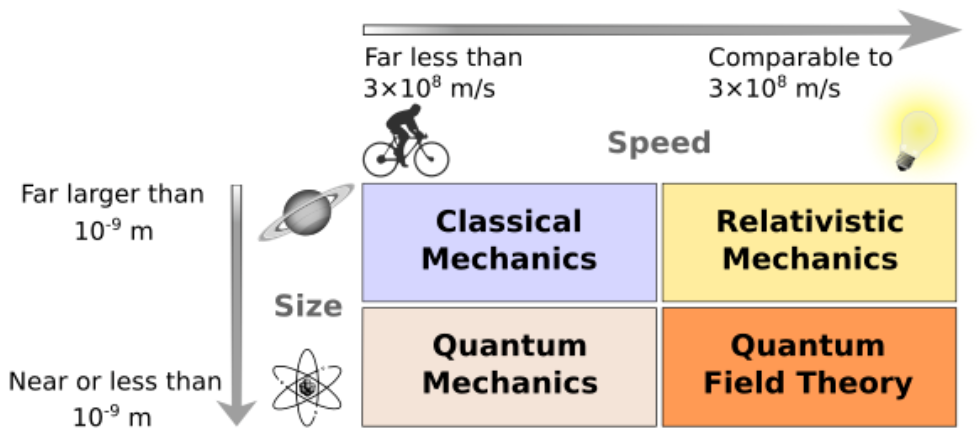
　　 如果一个遵循经典力学定律的物体的当前状态已知，就可以确定它将来的运动方式以及过去的运动轨迹。然而，混沌理论表明，经典力学对长期预测并不可靠。在研究非极端质量且速度未接近光速的物体时，经典力学能够提供精确的结果。当研究的对象接近原子直径大小时，就需要使用量子力学；而描述接近光速的速度时，则需要使用狭义相对论。当物体质量极大时，广义相对论则变得适用。一些现代文献将相对论力学归入经典物理学范畴，认为它是该领域最成熟和精确的形式。

1. 分支

传统划分

　　 经典力学传统上分为三个主要分支。静力学是经典力学的一个分支，研究作用在不加速的物理系统上的力和力矩的分析，这些系统与其环境处于平衡状态。[3] 运动学描述点、物体以及物体系统（物体群）的运动，而不考虑引起这些运动的力。[4][5][3] 作为一个研究领域，运动学常被称为 “运动的几何学”，有时甚至被视为数学的一个分支。[6][7][8] 动力学不仅仅描述物体的行为，还考虑解释这些行为的力。一些作者（例如 Taylor (2005)[9] 和 Greenwood (1997)[10]）将狭义相对论包含在经典动力学中。

力与能量

　　 另一种划分方法基于数学形式主义的选择。经典力学可以用多种不同的数学方式来表述。这些不同形式的物理内容是相同的，但它们提供了不同的洞察力，并有助于进行不同类型的计算。虽然 “牛顿力学” 一词有时被用作非相对论经典物理的同义词，但它也可以特指一种基于牛顿运动定律的特定形式主义。在这种意义上，牛顿力学强调力作为矢量量的重要性。[11]

　　 与之相对的是，解析力学利用描述系统整体运动的标量属性——通常是动能和势能。运动方程通过某种关于标量变化的基本原理从标量量推导出来。解析力学的两个主要分支是： 拉格朗日力学，它使用广义坐标和对应的广义速度，在配置空间中进行分析；哈密顿力学，它使用坐标和对应的广义动量，在相空间中进行分析。

　　 这两种表述通过对广义坐标、速度和动量进行勒让德变换是等价的；因此，两者包含描述系统动力学所需的相同信息。此外，还有其他表述方法，例如哈密顿-雅可比理论、鲁斯力学和阿佩尔运动方程。

　　 所有描述粒子和场运动的方程，无论采用何种形式主义，都可以从一种广泛适用的结果——最小作用量原理推导出来。一个重要的结果是诺特定理，它将守恒定律与它们所关联的对称性联系起来。

按应用领域划分

　　 另一种划分方式是根据应用领域：

2. 物体及其运动的描述

图
图 2：抛体运动的分析是经典力学的一部分。

　　 为了简化，经典力学通常将现实世界中的物体建模为点粒子，即大小可忽略不计的物体。点粒子的运动由少量参数决定：其位置、质量以及作用在其上的力。经典力学还描述了非点状扩展物体的更复杂运动。欧拉定律在这一领域对牛顿定律进行了扩展。角动量的概念依赖于与描述一维运动相同的微积分方法。火箭方程将物体动量变化率的概念扩展到包含物体 “损失质量” 的影响。（这些推广和扩展是通过将刚体分解为一组点粒子并基于牛顿定律推导出来的。）

　　 实际上，经典力学能够描述的物体总是具有非零的大小。（非常小的粒子，如电子，其行为更准确地由量子力学描述。）具有非零大小的物体因额外的自由度而表现出比假想的点粒子更复杂的行为。例如，一个棒球在运动的同时可以旋转。然而，通过将此类物体视为由大量协同作用的点粒子组成的复合物体，可以使用点粒子的结果来研究它们。复合物体的质心表现得像一个点粒子。

　　 经典力学假设物质和能量具有明确且可知的属性，例如在空间中的位置和速度。非相对论力学还假设力是瞬时作用的（参见远距作用）。

运动学

　　 点粒子的位置是相对于一个坐标系定义的，该坐标系以空间中任意固定的参考点作为原点 \( O \)。一个简单的坐标系可以通过一个标记为 \( \mathbf{r} \) 的矢量描述粒子 \( P \) 的位置，该矢量由一个箭头表示，从原点 \( O \) 指向点 \( P \)。一般来说，点粒子不需要相对于 \( O \) 静止。在 \( P \) 相对于 \( O \) 运动的情况下，\( \mathbf{r} \) 被定义为时间 \( t \) 的函数。在爱因斯坦相对论之前（称为伽利略相对论），时间被认为是绝对的，即，对于任意一对事件，所有观察者所观测到的时间间隔都是相同的。[12]

　　 除了依赖于绝对时间，经典力学还假设空间的结构遵循欧几里得几何。[13]

　　 速度与速率 速度（即位移随时间变化的速率）定义为位置对时间的导数： \[ \mathbf{v} = \frac{\mathrm{d} \mathbf{r}}{\mathrm{d} t}~ \] 在经典力学中，速度可以直接相加或相减。例如，一辆汽车以每小时 60 公里向东行驶，并超过另一辆以每小时 50 公里向东行驶的汽车，则较慢的汽车会感知较快的汽车以 \( 60 - 50 = 10 \) km/h 的速度向东运动。然而，从较快汽车的角度来看，较慢的汽车以 10 km/h 向西移动，通常表示为 \(-10 \) km/h，其中符号负号表示方向相反。

　　 作为矢量量，速度需要用矢量分析方法进行处理。

　　 数学上，如果将之前讨论中的第一个物体的速度表示为矢量 \(\mathbf{u} = u \mathbf{d}\)，第二个物体的速度表示为矢量 \(\mathbf{v} = v \mathbf{e}\)，其中 \(u\) 是第一个物体的速率，\(v\) 是第二个物体的速率，\(\mathbf{d}\) 和 \(\mathbf{e}\) 分别是两个物体运动方向的单位矢量，则第二个物体观察到的第一个物体的速度为： \[ \mathbf{u}' = \mathbf{u} - \mathbf{v}~ \] 类似地，第一个物体观察到的第二个物体的速度为： \[ \mathbf{v}' = \mathbf{v} - \mathbf{u}~ \] 当两个物体沿同一方向运动时，该公式可以简化为： \[ \mathbf{u}' = (u - v) \mathbf{d}~ \] 或者，忽略方向，仅以速率表示其差值： \[ u' = u - v~ \] 加速度 加速度，即速度的变化率，定义为速度对时间的导数（位置对时间的二阶导数）： \[ \mathbf{a} = \frac{\mathrm{d} \mathbf{v}}{\mathrm{d} t} = \frac{\mathrm{d}^2 \mathbf{r}}{\mathrm{d} t^2}~ \] 加速度表示速度随时间的变化。速度的变化可以表现为大小的变化、方向的变化，或两者同时变化。

　　 有时，速度大小的减小被称为减速（deceleration），但通常来说，任何随时间变化的速度，包括减速在内，统称为加速度。

　　 参考系

　　 虽然可以相对于任何状态运动的观察者描述粒子的位置、速度和加速度，经典力学假设存在一个特殊的参考系族，在其中自然的力学定律呈现出相对简单的形式。这些特殊的参考系被称为惯性参考系。惯性参考系是一个理想化的参考系，在其中，如果一个物体所受的合力为零，它将以恒定的速度运动；即，要么保持静止，要么沿直线做匀速运动。在惯性参考系中，牛顿运动定律 \( F = ma \) 是有效的。[14]: 185 

　　 非惯性参考系相对于某个惯性参考系加速运动。例如，一个相对于惯性参考系旋转的参考系并不是惯性参考系。[14] 从惯性参考系观察，非惯性参考系中的粒子似乎以不能通过现有力场解释的方式运动，因此方程中似乎出现了额外的力，这些力仅仅是相对加速度的结果。这些力被称为虚拟力、惯性力或伪力。

　　 考虑两个参考系 \( S \) 和 \( S' \)。对于每个参考系中的观察者，一个事件在参考系 \( S \) 中的时空坐标为 \( (x, y, z, t) \)，在 \( S' \) 中的时空坐标为 \( (x', y', z', t') \)。假设在所有参考系中时间的测量方式相同，并且在 \( t = 0 \) 时满足 \( x = x' \)，那么在参考系 \( S \) 和 \( S' \)（两者以相对速度 \( u \) 沿 \( x \) 方向运动）中观察到的同一事件的时空坐标关系为： \[ \begin{aligned} x' &= x - tu, \\ y' &= y, \\ z' &= z, \\ t' &= t. \end{aligned}~ \] 这一组公式定义了一种称为伽利略变换的群变换（非正式称为伽利略变换）。该群是狭义相对论中庞加莱群的一个极限情况，当速度 \( u \) 远小于光速 \( c \) 时适用。

　　 这些变换带来了以下结果：

　　 对于某些问题，使用旋转坐标系（参考系）会更加方便。这样可以选择保留到一个惯性参考系的映射，或者额外引入虚拟离心力和科里奥利力。

3. 牛顿力学

　　 在物理学中，力是指引起物体速度变化（即加速）的任何作用。力源于某种场，例如静电场（由静电荷产生）、电磁场（由运动电荷产生）或引力场（由质量产生）等。

　　 牛顿是第一个用数学表达力与动量关系的人。一些物理学家将牛顿第二定律视为力和质量的定义，而另一些人将其看作一个基本假设，即自然法则。[15] 无论哪种解释，其数学表达都是相同的，历史上称为 “牛顿第二定律”： \[ \mathbf{F} = \frac{\mathrm{d} \mathbf{p}}{\mathrm{d} t} = \frac{\mathrm{d} (m\mathbf{v})}{\mathrm{d} t}~ \] 其中，\( m\mathbf{v} \) 被称为（标准）动量。因此，作用在粒子上的合力等于粒子动量随时间的变化率。由于加速度的定义为 \( \mathbf{a} = \frac{\mathrm{d} \mathbf{v}}{\mathrm{d} t} \)，第二定律可以写成更简化和常见的形式： \[ \mathbf{F} = m\mathbf{a}~ \] 只要作用在粒子上的力是已知的，牛顿第二定律就足以描述粒子的运动。一旦可以获得每个作用力的独立关系，就可以将它们代入牛顿第二定律，得到一个常微分方程，这个方程被称为运动方程。

　　 示例：假设摩擦力是作用在粒子上的唯一力，并且摩擦力可以表示为粒子速度的函数，例如： \[ \mathbf{F}_{\mathrm{R}} = -\lambda \mathbf{v}~ \] 其中 \( \lambda \) 是一个正常数，负号表明力的方向与速度的方向相反。此时，运动方程为： \[ -\lambda \mathbf{v} = m\mathbf{a} = m\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} t}~ \] 将其积分可以得到： \[ \mathbf{v} = \mathbf{v}_0 e^{-\lambda t / m}~ \] 其中，\( \mathbf{v}_0 \) 是初速度。这意味着，随着时间的推移，粒子的速度以指数形式衰减为零。在这种情况下，等效的观点是粒子的动能被摩擦力吸收，并根据能量守恒定律转化为热能，从而导致粒子减速。通过进一步积分，还可以得到粒子的位置 \( \mathbf{r} \) 随时间的变化关系。

　　 重要的力包括引力和用于描述电磁现象的洛伦兹力。此外，牛顿第三定律有时可以用来推导作用在粒子上的力：如果已知粒子 \( A \) 对另一个粒子 \( B \) 施加了力 \( \mathbf{F} \)，则 \( B \) 必须对 \( A \) 施加大小相等、方向相反的反作用力 \( -\mathbf{F} \)。牛顿第三定律的强形式要求 \( \mathbf{F} \) 和 \( -\mathbf{F} \) 沿 \( A \) 和 \( B \) 的连线作用，而弱形式则没有这样的要求。弱形式的牛顿第三定律的例子通常可以在磁力中找到。[需要澄清]

功与能量

　　 如果对粒子施加一个恒定力 \( \mathbf{F} \)，使其产生位移 \( \Delta \mathbf{r} \)（注释 1），则力所做的功定义为力矢量与位移矢量的标量积： \[ W = \mathbf{F} \cdot \Delta \mathbf{r}~ \] 更一般地说，如果粒子从位置 \( \mathbf{r}_1 \) 沿路径 \( C \) 移动到位置 \( \mathbf{r}_2 \)，而力随位置变化，则作用在粒子上的功由线积分给出： \[ W = \int_{C} \mathbf{F}(\mathbf{r}) \cdot \mathrm{d} \mathbf{r}~ \] 如果从 \( \mathbf{r}_1 \) 到 \( \mathbf{r}_2 \) 的功与路径无关，则称该力为保守力。重力是保守力，理想弹簧的弹力（由胡克定律描述）也是保守力，而摩擦力是非保守力。

　　 粒子质量为 \( m \)，速度为 \( v \) 时，其动能 \( E_k \) 为： \[ E_k = \frac{1}{2} m v^2~ \] 对于由多个粒子组成的扩展物体，其总动能为所有粒子动能的总和。

　　 功-能定理指出，对于质量 \( m \) 不变的粒子，从位置 \( \mathbf{r}_1 \) 移动到 \( \mathbf{r}_2 \) 所做的总功 \( W \) 等于粒子动能的变化 \( \Delta E_k \)： \[ W = \Delta E_k = E_{k2} - E_{k1} = \frac{1}{2} m \left(v_2^2 - v_1^2\right)~ \] 保守力可以表示为一个标量函数（称为势能）的梯度，记作 \( E_p \)： \[ \mathbf{F} = -\mathbf{\nabla} E_p~ \] 如果作用在粒子上的所有力都是保守力，且 \( E_p \) 为总势能（定义为作用力通过重新排列物体间位置所做的功），则通过对每个力的势能求和可以得到： \[ \mathbf{F} \cdot \Delta \mathbf{r} = -\mathbf{\nabla} E_p \cdot \Delta \mathbf{r} = -\Delta E_p~ \] 势能的减少等于动能的增加： \[ -\Delta E_p = \Delta E_k \implies \Delta (E_k + E_p) = 0~ \] 这个结果被称为能量守恒定律，表明总能量： \[ \sum E = E_k + E_p~ \] 在时间上是恒定的。这一定律非常有用，因为许多常见的力是保守力。

4. 拉格朗日力学

　　 拉格朗日力学是一种基于驻定作用原理（也称为最小作用原理）的经典力学表述。这一理论由意大利-法国数学家和天文学家约瑟夫-路易·拉格朗日（Joseph-Louis Lagrange）于 1760 年在其向都灵科学院的报告中首次提出，[16] 并在 1788 年的重要著作《分析力学》（Mécanique analytique）中得到总结。

　　 拉格朗日力学将一个力学系统描述为一个由配置空间 \( M \) 和其中的一个平滑函数 \( L \)（称为拉格朗日量）组成的对 \( (M, L) \)。对于许多系统，拉格朗日量可以表示为： \[ L = T - V~ \] 其中，\( T \) 是系统的动能，\( V \) 是系统的势能。

　　 驻定作用原理要求系统从拉格朗日量 \( L \) 派生出的作用量泛函在系统的时间演化过程中保持在一个驻定点（即最大值、最小值或鞍点）。这一约束条件允许通过拉格朗日方程计算系统的运动方程。[17]

5. 哈密顿力学

　　 哈密顿力学于 1833 年作为拉格朗日力学的重新表述而出现，由威廉·罗恩·哈密顿爵士（Sir William Rowan Hamilton）提出。[18] 在哈密顿力学中，拉格朗日力学中的（广义）速度 \( \dot{q}^i \) 被替换为（广义）动量。两种理论都是经典力学的解释方式，并描述相同的物理现象。哈密顿力学与几何学（特别是辛几何和泊松结构）关系密切，是经典力学与量子力学之间的一个桥梁。

　　 在这种形式主义中，系统的动力学由哈密顿方程控制，这些方程用一个称为哈密顿量的函数的偏导数表达位置和动量变量的时间导数： \[ \frac{\mathrm{d} \boldsymbol{q}}{\mathrm{d} t} = \frac{\partial \mathcal{H}}{\partial \boldsymbol{p}}, \quad \frac{\mathrm{d} \boldsymbol{p}}{\mathrm{d} t} = -\frac{\partial \mathcal{H}}{\partial \boldsymbol{q}}~ \] 哈密顿量是拉格朗日量的勒让德变换。在许多物理感兴趣的情况下，哈密顿量等于系统的总能量。

6. 适用性限制

图
图 3：经典力学的适用范围

　　 经典力学的许多分支是更精确形式的简化或近似，其中最精确的形式之一是广义相对论和相对论统计力学。几何光学是光量子理论的一种近似，并不存在更优越的 “经典” 形式。

　　 当量子力学和经典力学都无法适用时，例如在具有许多自由度的量子层面上，量子场论（QFT）可以发挥作用。量子场论处理小距离、高速运动以及具有多个自由度的情况，同时还允许在相互作用中粒子数的变化可能性。

　　 在宏观层面处理大量自由度时，统计力学变得有用。统计力学描述了大量（但可数）粒子及其整体相互作用在宏观层面的行为。统计力学主要用于热力学，尤其是当系统超出经典热力学假设范围时。

　　 当高速物体的速度接近光速时，经典力学通过狭义相对论进行扩展。当物体的质量极大（即其施瓦西半径在给定应用中不再可以忽略不计）时，偏离牛顿力学的现象会显现，此时可以通过参数化后牛顿形式主义进行量化。在这种情况下，广义相对论（GR）变得适用。

　　 然而，迄今为止，还没有一种能够统一广义相对论和量子场论的量子引力理论，可以用来描述既极小又极重的物体。[4][5]

牛顿力学对狭义相对论的近似

　　 在狭义相对论中，粒子的动量由以下公式给出： \[ \mathbf{p} = \frac{m\mathbf{v}}{\sqrt{1 - \frac{v^2}{c^2}}}~ \] 其中，\( m \) 是粒子的静止质量，\( \mathbf{v} \) 是其速度矢量，\( v \) 是 \( \mathbf{v} \) 的大小，\( c \) 是光速。

　　 当 \( v \) 相对于 \( c \) 非常小时，\( \frac{v^2}{c^2} \) 可以近似为零，因此： \[ \mathbf{p} \approx m\mathbf{v}~ \] 由此可见，对于速度远小于光速的物体，牛顿公式 \( \mathbf{p} = m\mathbf{v} \) 是狭义相对论公式的近似。

　　 例如，回旋加速器（cyclotron）、陀螺管（gyrotron）或高压磁控管（magnetron）的相对论回旋频率可以表示为： \[ f = f_{\mathrm{c}} \frac{m_0}{m_0 + \frac{T}{c^2}}~ \] 其中，\( f_{\mathrm{c}} \) 是粒子（如电子）在磁场中绕圈的经典频率，\( T \) 是其动能，\( m_0 \) 是粒子的（静止）质量。

　　 以电子为例，其（静止）质量为 511 keV。因此，对于加速电压为 5.11 kV 的磁控管，频率校正约为 1%。

经典力学对量子力学的近似

　　 当德布罗意波长不再远小于系统的其他特征尺寸时，经典力学中的射线近似失效。对于非相对论性粒子，德布罗意波长由以下公式表示： \[ \lambda = \frac{h}{p}~ \] 其中，\( h \) 是普朗克常数，\( p \) 是动量。

　　 这种现象在电子中比在较重的粒子中更早发生。例如，1927 年克林顿·戴维森（Clinton Davisson）和莱斯特·革末（Lester Germer）通过 54 伏加速的电子，其波长为 0.167 nm，与镍晶体原子间距 0.215 nm 的晶面反射时，足够表现出一个单独的衍射旁瓣。如果使用更大的真空腔室，将角分辨率从约 1 弧度提高到 1 毫弧度，可能可以观测到集成电路存储器中周期性图案的量子衍射。

　　 在工程领域，经典力学失效的更实用的例子包括隧道二极管中通过量子隧穿效应的导电现象，以及集成电路中非常窄的晶体管栅极。

　　 经典力学与几何光学具有相同的极高频近似特性。它通常更准确，因为经典力学描述了具有静止质量的粒子和物体。这些粒子具有更大的动量，因此与同等动能的无质量粒子（如光子）相比，其德布罗意波长更短。

7. 历史

　　 对物体运动的研究可以追溯到古代，使经典力学成为科学、工程和技术中最古老、最广泛的学科之一。经典力学的发展还促进了许多数学领域的产生。[19]: 54

　　 一些古希腊哲学家（其中包括亚里士多德，他是亚里士多德物理学的创始人）可能是最早提出 “万物皆有因” 的观点的人，并认为理论原则有助于理解自然。尽管对于现代读者而言，这些保留下来的思想显得非常合理，但显著的是，它们缺乏我们现在所熟知的数学理论和受控实验。这些因素后来成为形成现代科学的决定性因素，其早期应用被称为经典力学。在他的著作《论重力的元素》（*Elementa super demonstrationem ponderum*）中，中世纪数学家约尔达努斯·德·内莫尔（Jordanus de Nemore）引入了 “位置重力”（positional gravity）的概念，并开始使用分力分析方法。

图
图 4：阿尔伯特·萨克森的三阶段冲力理论

　　 关于行星运动的第一个因果解释由约翰内斯·开普勒在 1609 年出版的《新天文学》（Astronomia nova）中提出。他基于第谷·布拉赫对火星轨道的观测得出结论：行星的轨道是椭圆形的。这一突破性的观点与古代思想决裂，与此同时，伽利略正在提出关于物体运动的抽象数学定律。他可能（也可能没有）进行过著名的比萨斜塔实验，通过从塔上同时投下两颗不同重量的炮弹，展示它们同时落地。尽管这一具体实验的真实性存在争议，但他确实通过在斜面上滚动小球进行定量实验。他的加速运动理论正是基于这些实验的结果，并成为经典力学的基石之一。

　　 1673 年，克里斯蒂安·惠更斯在其著作《摆钟》（Horologium Oscillatorium）中描述了第一和第二运动定律。[20] 该著作也是第一部现代意义上的论文，其中将一个物理问题（自由落体的加速运动）通过一组参数进行理想化处理，然后进行数学分析。这部作品构成了应用数学领域的重要奠基之作之一。[21]

图
图 5：艾萨克·牛顿爵士（1643–1727），物理学史上具有重要影响的人物，其三大运动定律构成了经典力学的基础。

　　 牛顿在三条运动定律的基础上构建了其自然哲学的原则：惯性定律、上文提到的加速度定律（第二定律），以及作用与反作用定律。他为经典力学奠定了基础。牛顿在其《自然哲学的数学原理》（Philosophiæ Naturalis Principia Mathematica）中对第二和第三定律进行了科学和数学上的严格处理，从而区别于之前试图解释类似现象的尝试，这些尝试通常是不完整的、不正确的，或者缺乏精确的数学表达。牛顿还阐述了动量守恒定律和角动量守恒定律的原则。

　　 在力学领域，牛顿是第一个正确科学地和数学地表述万有引力定律的人。牛顿运动定律和引力定律的结合为经典力学提供了最全面、最准确的描述。他证明了这些定律既适用于日常物体，也适用于天体物体。特别是，他为开普勒行星运动定律提供了理论解释。

　　 牛顿早先发明了微积分，但《数学原理》的表述完全基于长期确立的几何方法，以效仿欧几里得的风格。牛顿及其大多数同时代人（克里斯蒂安·惠更斯是一个显著例外）都认为经典力学可以解释所有现象，包括以几何光学形式描述的光学现象。即使在发现了所谓的牛顿环（一种波的干涉现象）后，他仍然坚持自己的粒子光学理论。

图
图 6：拉格朗日的贡献在于用现代数学的语言实现了牛顿的思想，这种方法现在被称为拉格朗日力学。

　　 一些在 19 世纪后期发现的问题只能通过更现代的物理学加以解决。其中一些问题与电磁理论的兼容性有关，例如著名的迈克尔逊-莫雷实验。这些问题的解决催生了狭义相对论，这通常仍被视为经典力学的一部分。

　　 另一类问题与热力学有关。当经典力学与热力学结合时，出现了吉布斯悖论（Gibbs paradox）这一经典统计力学中的问题，导致熵无法成为一个良定义的量。此外，黑体辐射无法在不引入量子的情况下得到解释。随着实验深入到原子尺度，经典力学甚至无法近似解释一些基本现象，例如原子的能级、原子的大小以及光电效应。解决这些问题的努力最终促成了量子力学的发展。

图
图 7：哈密顿提出了一种不同于拉格朗日力学的表述方法，现在被称为哈密顿力学。

　　 自 20 世纪末以来，经典力学在物理学中不再被视为一门独立的理论。相反，经典力学现在被认为是更广义的量子力学的近似理论。研究重点已转向理解自然的基本力，例如标准模型及其更现代的扩展——统一理论（即 “万物理论”）。经典力学是一种有用的理论，适用于研究非量子力学、低能粒子在弱引力场中的运动。

8. 另见

9. 注释

10. 参考文献：

　　
1. Ben-Chaim, Michael (2004), 实验哲学与经验科学的诞生：波义耳、洛克和牛顿，奥尔德肖特：Ashgate 出版社，ISBN 0-7546-4091-4, OCLC 53887772。
2. Agar, Jon (2012), 20 世纪及以后的科学，剑桥：Polity 出版社，ISBN 978-0-7456-3469-2。
3. Thomas Wallace Wright (1896), 力学元素，包括运动学、动力学和静力学：及其应用，E. and F. N. Spon 出版社，第 85 页。
4. Edmund Taylor Whittaker (1904), 粒子与刚体的分析动力学论，剑桥大学出版社，第 1 章，ISBN 0-521-35883-3。
5. Joseph Stiles Beggs (1983), 运动学，Taylor & Francis 出版社，第 1 页，ISBN 0-89116-355-7。
6. Russell C. Hibbeler (2009), “粒子运动学与动力学”，《工程力学：动力学》（第 12 版），Prentice Hall 出版社，第 298 页，ISBN 978-0-13-607791-6。
7. Ahmed A. Shabana (2003), “参考运动学”，《多体系统动力学》（第 2 版），剑桥大学出版社，ISBN 978-0-521-54411-5。
8. P. P. Teodorescu (2007), “运动学”，《机械系统，经典模型：粒子力学》，Springer 出版社，第 287 页，ISBN 978-1-4020-5441-9。
9. John Robert Taylor (2005), 经典力学，University Science Books 出版社，ISBN 978-1-891389-22-1。
10. Donald T Greenwood (1997), 经典力学（1977 年版重印），Courier Dover Publications，第 1 页，ISBN 0-486-69690-1。
11. Lanczos, Cornelius (1970), 力学的变分原理（第 4 版），纽约：Dover Publications Inc.，引言部分，第 xxi 至 xxix 页，ISBN 0-486-65067-7。
12. Knudsen, Jens M.; Hjorth, Poul (2012), 牛顿力学要素（插图版），Springer Science & Business Media，第 30 页，ISBN 978-3-642-97599-8。
13. 麻省理工学院物理学 8.01 讲义（第 12 页），存档于 2013 年 7 月 9 日，美国国会图书馆网络档案馆。
14. Goldstein, Herbert (1950), 经典力学（第 1 版），Addison-Wesley 出版。
15. Thornton, Stephen T.; Marion, Jerry B. (2004), 粒子与系统的经典动力学（第 5 版），Belmont, CA: Brooks/Cole 出版社，第 50 页，ISBN 978-0-534-40896-1。
16. Fraser, Craig (1983), “J.L.拉格朗日在力学原理与方法方面的早期贡献”，《精确科学史档案》，第 28 卷（第 3 期）：197–241，doi:10.1007/BF00328268，JSTOR 41133689。
17. Hand, L. N.; Finch, J. D. (1998), 解析力学（第 2 版），剑桥大学出版社，第 18–20, 23, 46, 51 页，ISBN 9780521575720。
18. Hamilton, William Rowan (1833), 关于用特征函数系数表达光路径和行星路径的一种通用方法，P.D. Hardy 印刷，OCLC 68159539。
19. Doran, Chris; Lasenby, Anthony N. (2003), 物理学家的几何代数，剑桥纽约：剑桥大学出版社，ISBN 978-0-521-48022-2。
20. Rob Iliffe & George E. Smith (2016), 牛顿的剑桥指南，剑桥大学出版社，第 75 页，ISBN 9781107015463。
21.Yoder, Joella G. (1988). 《时间的展开：克里斯蒂安·惠更斯与自然的数学化》，剑桥：剑桥大学出版社，ISBN 978-0-521-34140-0。

11. 进一步阅读

12. 外部链接

                     

© 小时科技 保留一切权利