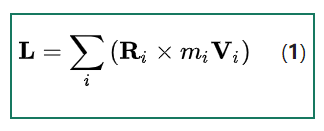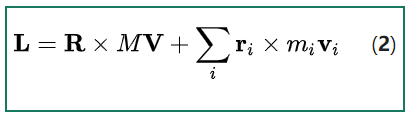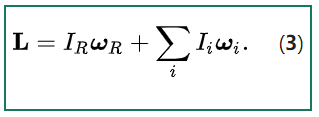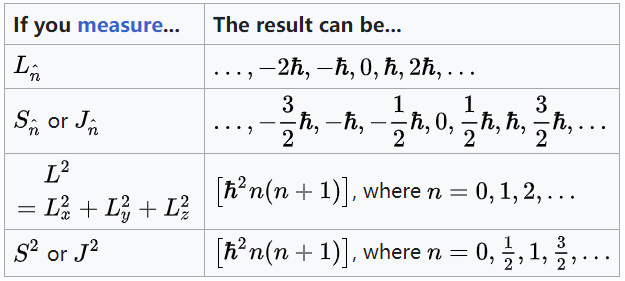角动量(综述)
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章)
角动量(有时称为动量矩或旋转动量)是线性动量的旋转类比。它是一个重要的物理量,因为它是守恒量——封闭系统的总角动量保持不变。角动量既有方向也有大小,并且两者都守恒。自行车和摩托车、飞盘、膛线子弹以及陀螺仪的有用特性都归因于角动量守恒。角动量守恒也是飓风形成螺旋状以及中子星具有高速旋转率的原因。通常,守恒定律限制了系统可能的运动,但并不能唯一确定其运动方式。
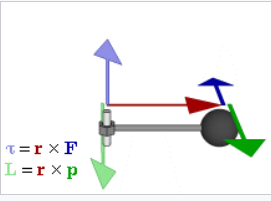
三维角动量在经典力学中表示为伪向量 \( \mathbf{r} \times \mathbf{p} \),即粒子位置向量 \( \mathbf{r} \)(相对于某一原点)与其动量向量的叉积;后者在牛顿力学中为 \( \mathbf{p} = m\mathbf{v} \)。与线性动量不同,角动量取决于原点的选择,因为粒子的位置是从该原点测量的。
角动量是一种广延量;也就是说,任何复合系统的总角动量是其组成部分角动量的总和。对于连续的刚体或流体,系统的总角动量是角动量密度(即单位体积的角动量,当体积趋近于零时)的体积分在整个物体上的积分。
类似于线性动量守恒,如果没有外力作用,线性动量守恒;同样,如果没有外力矩作用,角动量也守恒。力矩可以定义为角动量的变化率,类似于力的作用。任何系统的净外力矩始终等于系统上的总力矩;系统内的所有内力矩之和总是为 0(这是牛顿第三运动定律的旋转类比)。因此,对于封闭系统(没有净外力矩),系统的总力矩必须为 0,这意味着系统的总角动量是恒定的。
特定相互作用下角动量的变化称为角冲量,有时称为 “旋转”。角冲量是线性冲量的旋转类比。[3]
1. 示例
对于一个处于轨道中的物体,其角动量 \( L \) 的简单情况表示为: \[ L = 2\pi Mfr^2~ \] 其中,\( M \) 是轨道物体的质量,\( f \) 是轨道的频率,\( r \) 是轨道的半径。
对于一个绕其轴旋转的均匀刚性球体,其角动量 \( L \) 表示为: \[ L = \frac{4}{5} \pi Mfr^2~ \] 其中,\( M \) 是球体的质量,\( f \) 是旋转的频率,\( r \) 是球体的半径。
例如,地球相对于太阳的轨道角动量约为 \( 2.66 \times 10^{40} \) kg⋅m²⋅s⁻¹,而地球的自转角动量约为 \( 7.05 \times 10^{33} \) kg⋅m²⋅s⁻¹。
对于一个绕其轴旋转的均匀刚性球体,如果已知其密度而非质量,其角动量 \( L \) 表示为: \[ L = \frac{16}{15} \pi^2 \rho fr^5~ \] 其中,\( \rho \) 是球体的密度,\( f \) 是旋转频率,\( r \) 是球体的半径。
对于最简单的旋转圆盘,角动量 \( L \) 表示为:[4] \[ L = \pi Mfr^2~ \] 其中,\( M \) 是圆盘的质量,\( f \) 是旋转频率,\( r \) 是圆盘的半径。
如果圆盘绕其直径旋转(例如抛硬币时),其角动量 \( L \) 表示为:[4] \[ L = \frac{1}{2} \pi Mfr^2~ \]
2. 经典力学中的定义
“轨道角动量” 重定向至此。关于其他用途,参见轨道角动量(消歧义)。
“自旋角动量” 重定向至此。关于其他用途,参见自旋角动量(消歧义)。
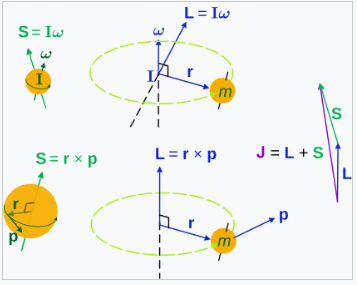
正如角速度一样,物体的角动量有两种特殊类型:自旋角动量是相对于物体质心的角动量,而轨道角动量是相对于选定旋转中心的角动量。例如,地球因为围绕太阳公转而具有轨道角动量,同时由于每天绕极轴自转而具有自旋角动量。总角动量是自旋角动量和轨道角动量的总和。在地球的情况下,主要守恒量是太阳系的总角动量,因为行星与太阳之间会有少量但重要的角动量交换。质点的轨道角动量矢量始终与其轨道角速度矢量 \( \omega \) 平行且成正比,比例常数取决于粒子的质量和其距离原点的距离。刚体的自旋角动量矢量与自旋角速度矢量 \( \Omega \) 成正比,但不总是平行,因此比例常数是一个二阶张量而非标量。
3. 二维中的轨道角动量
角动量是一个矢量量(更准确地说是伪矢量),它表示物体的转动惯量与绕某特定轴的转速(以弧度/秒为单位)的乘积。然而,如果粒子的轨迹位于一个平面内,则可以忽略角动量的矢量性质,将其作为标量(更准确地说是伪标量)处理。[5] 角动量可以看作是线性动量的旋转类比。因此,线性动量 \( p \) 与质量 \( m \) 和线速度 \( v \) 成正比: \[ p = mv,~ \]
角动量 \( L \) 与转动惯量 \( I \) 和以弧度/秒为单位的角速度 \( \omega \) 成正比。[6] \[ L = I\omega.~ \]
与只依赖物质数量的质量不同,转动惯量还取决于旋转轴的位置以及物质的分布。与不依赖原点选择的线速度不同,轨道角速度总是相对于固定原点测量。因此,严格来说,\( L \) 应被称为相对于该中心的角动量。[7]
对于单个粒子的圆周运动,可以使用 \(I = r^2 m\) 和 \(\omega = v/r\) 来展开角动量为 \(L = r^2 m \cdot v/r\) 简化为: \[ L = rmv.~ \] 角动量是旋转半径 \( r \) 和粒子的线动量 \( p = mv \) 的乘积,其中 \(v = r\omega\) 是线速度(切向速度)。
如果使用与半径向量垂直的运动分量,这种简单的分析也适用于非圆周运动: \[ L = rmv_{\perp},~ \] 其中 \(v_{\perp} = v \sin\left(\theta\right) \) 是运动的垂直分量。展开为:\(L = rmv \sin\left(\theta\right) \),重新排列后为:\(L = r \sin\left(\theta\right) mv\),简化后,角动量也可以表示为: \[ L = r_{\perp} mv,~ \] 其中 \(r_{\perp} = r \sin\left(\theta\right) \) 是力矩臂的长度,即从原点垂直投影到粒子轨迹上的线段。这个定义(力矩臂长度 × 线动量)即为 “动量矩” 一词的来源。[8]
来自拉格朗日力学的标量角动量
另一种方法是将角动量定义为机械系统的角坐标 \(\phi\) 的共轭动量(也称为正则动量)。考虑一个质量为 \(m\) 的机械系统,它被约束在半径为 \(r\) 的圆上运动,且没有外部力场的存在。系统的动能为” \[ T = \frac{1}{2}mr^2\omega^2 = \frac{1}{2}mr^2{\dot{\phi}}^2. ~\] 势能为: \[ U = 0.~ \] 因此,拉格朗日量为: \[ \mathcal{L}(\phi, \dot{\phi}) = T - U = \frac{1}{2}mr^2{\dot{\phi}}^2. ~\] 广义动量,即与坐标 \(\phi\) 正则共轭的动量,定义为: \[ p_\phi = \frac{\partial \mathcal{L}}{\partial \dot{\phi}} = mr^2{\dot{\phi}} = I\omega = L.~ \] 这里,\(L\) 是角动量,\(I\) 是转动惯量,\(\omega\) 是角速度。
轨道角动量在三维空间中的描述
要完全定义三维中的轨道角动量,需要知道位置向量扫过角度的速率、垂直于瞬时角位移平面的方向、相关的质量以及该质量在空间中的分布情况。[9] 通过保留角动量的向量性质,可以保留方程的一般性质,从而能够描述绕旋转中心的任何类型的三维运动——无论是圆周运动、线性运动还是其他形式的运动。用向量表示法,绕原点运动的点质点的轨道角动量可以表示为: \[ \mathbf {L} = I{\boldsymbol {\omega }}, ~\] 其中:
- \(I = r^2 m\) 是质点的转动惯量,
- \({\boldsymbol {\omega }} = \frac {\mathbf {r} \times \mathbf {v} }{r^2}\) 是该质点绕原点的轨道角速度,
- \(\mathbf {r} \) 是质点相对于原点的位置向量,\(r = |\mathbf {r}|\) 是位置向量的模,
- \(\mathbf {v} \) 是质点相对于原点的线速度,
- \(m \) 是质点的质量。
这个表达式可以展开、化简,并通过向量代数的规则重新排列: \[ \mathbf {L} = \left(r^2 m\right)\left(\frac {\mathbf {r} \times \mathbf {v} }{r^2}\right) = m\left(\mathbf {r} \times \mathbf {v} \right) = \mathbf {r} \times m\mathbf {v} = \mathbf {r} \times \mathbf {p},~ \] 其中,\(\mathbf {p}\) 是质点的动量。
这是位置向量 \( \mathbf{r} \) 和粒子的线动量 \( \mathbf{p} = m\mathbf{v} \) 的叉积。根据叉积的定义,角动量向量 \( \mathbf{L} \) 垂直于 \( \mathbf{r} \) 和 \( \mathbf{p} \)。它的方向垂直于角位移的平面,按照右手法则指示的方向——因此角速度从向量的顶端看是逆时针的。相反,角动量向量 \( \mathbf{L} \) 定义了 \( \mathbf{r} \) 和 \( \mathbf{p} \) 所在的平面。
通过定义一个垂直于角位移平面的单位向量 \( \mathbf{\hat{u}} \),可以得到一个标量角速度 \( \omega \),其公式为 \(\omega \mathbf{\hat{u}} = {\boldsymbol{\omega}},\) 并且 \(\omega = \frac{v_{\perp}}{r}, \) 其中 \( v_{\perp} \) 是运动的垂直分量,如上所述。
因此,前一节中的二维标量方程可以赋予方向: \[ \mathbf{L} = I{\boldsymbol{\omega}} = I\omega \mathbf{\hat{u}} = \left(r^{2}m\right)\omega \mathbf{\hat{u}} = rmv_{\perp} \mathbf{\hat{u}} = r_{\perp}mv \mathbf{\hat{u}},~ \] 对于圆周运动,其中所有运动都垂直于半径 \( r \)。
在球坐标系中,角动量向量表达为: \[ \mathbf{L} = m\mathbf{r} \times \mathbf{v} = mr^{2} \left( \dot{\theta} \, {\hat{\boldsymbol{\varphi}}} - \dot{\varphi} \sin \theta \, \mathbf{\hat{\boldsymbol{\theta}}} \right).~ \]
4. 与线性动量的类比
角动量可以描述为线性动量的旋转类比。与线性动量类似,它涉及质量和位移的元素。不像线性动量,它还涉及位置和形状的元素。
物理学中的许多问题涉及围绕某个空间点的物质运动,无论是实际围绕它旋转,还是简单地经过它,在这些情况下需要知道移动的物质对该点有什么影响——它是否可以对该点施加能量或在其周围做功?能量,即做功的能力,可以通过让物质运动来储存——这是一种惯性和位移的组合。惯性通过其质量来衡量,位移通过其速度来衡量。它们的乘积:
(惯量) × (位移量) = (惯量·位移量) 质量 × 速度 = 动量 \( m \times v = p \)
是物质的动量。[10] 将这个动量参照一个中心点会引入一个复杂性:动量并不是直接作用在该点上的。例如,一个位于车轮外缘的物质颗粒实际上位于一个与车轮半径相同长度的杠杆的末端,其动量使杠杆围绕中心点旋转。这个假想的杠杆被称为力臂。它的效果是按其长度的比例放大动量的作用,这种效果被称为力矩。因此,物质颗粒相对于某个特定点的动量为:
(力臂)×(惯量)×(位移量)=(惯量·位移量的力矩) 长度 × 质量 × 速度 = 动量矩 \( r \times m \times v = L \)
角动量,有时也被称为相对于特定中心点的动量矩。方程 \( L = rmv \) 将力矩(质量 \( m \) 旋转力臂 \( r \))与线性(直线等效)速度 \( v \) 结合起来。相对于中心点的线速度只是距离 \( r \) 和相对于该点的角速度 \( \omega \) 的乘积: \( v = r\omega \),这也是一个力矩。因此,角动量包含双重力矩: \( L = rmr\omega \)。 稍作简化,\( L = r^{2}m\omega \),其中量 \( r^{2}m \) 是粒子的转动惯量,有时也被称为质量的二阶矩。它是旋转惯性的量度。[11]
上述平移动量和旋转动量的类比可以用矢量形式表示:[需要引用]
- \(\mathbf{p} = m\mathbf{v} \)(线性运动中的动量)
- \( \mathbf{L} = I{\boldsymbol{\omega}} \)(旋转中的角动量)
动量的方向与线性运动中的速度方向相关,而角动量的方向与旋转的角速度相关。
由于转动惯量是自旋角动量的关键部分,后者必然包含前者的所有复杂性。转动惯量是通过将质量的基本部分与它们到旋转中心的距离的平方相乘来计算的。因此,总的转动惯量和角动量是关于物质配置及其旋转方向的复杂函数。
对于刚体,例如一个轮子或小行星,旋转的方向只是相对于物体本身物质的旋转轴的位置。这个轴可能穿过质心,也可能不穿过,甚至可能完全位于物体之外。对于同一个物体,角动量可能会对每一个可能的旋转轴取不同的值。当旋转轴通过质心时,角动量达到最小值。
对于围绕某个中心旋转的物体集合,例如太阳系中的所有天体,旋转的方向可能是有些组织化的,就像太阳系一样,大多数天体的旋转轴接近系统的轴。它们的方向也可能完全随机。
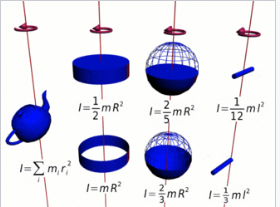
简言之,质量越大,距离旋转中心越远(即力臂越长),则转动惯量越大,因此在给定的角速度下,角动量越大。在许多情况下,转动惯量以及角动量可以简化为 \[ I = k^2 m,~ \] 其中 \( k \) 是回转半径,即可以认为整个质量 \( m \) 集中在距离轴的距离。
类似地,对于一个点质量 \( m \),转动惯量定义为 \[ I = r^2 m,~\] 其中 \( r \) 是点质量距离旋转中心的半径。
对于任意多个粒子 \( m_i \),转动惯量为各粒子的总和: \[ \sum_{i} I_i = \sum_{i} r_i^2 m_i. ~\] 角动量对位置和形状的依赖性反映在其单位与线动量的单位差异上:角动量的单位是 kg⋅m²/s 或 N⋅m⋅s,而线动量的单位是 kg⋅m/s 或 N⋅s。当计算角动量时,使用转动惯量乘以角速度,角速度必须以弧度每秒表示,其中弧度被视为无量纲单位,取值为 1。(在进行量纲分析时,可以使用将弧度视为基本单位的方向分析,但这在国际单位制中并不使用。)角动量的单位可以解释为力矩⋅时间。具有角动量 L N⋅m⋅s 的物体可以通过一个大小为 L N⋅m⋅s 的角冲量将其角速度降为零。
垂直于角动量轴并通过质心的平面有时被称为不变平面,因为如果只考虑系统内部物体之间的相互作用,而不受外部影响,该轴的方向将保持不变。其中一个这样的平面是太阳系的不变平面。
角动量与力矩
牛顿第二运动定律可以通过以下数学公式表达: \[ F = ma ~\] 即,力 = 质量 × 加速度。对于点粒子,旋转等效方程可以推导如下: \[ L = I\omega ~\] 这意味着力矩(即角动量的时间导数)为: \[ \tau = \frac{dI}{dt} \omega + I\frac{d\omega}{dt} ~\] 由于转动惯量是 \( I = mr^2 \),因此: \[ \frac{dI}{dt} = 2mr\frac{dr}{dt} = 2rp_{\parallel} ~\] 并且: \[ \frac{dL}{dt} = I\frac{d\omega}{dt} + 2rp_{\parallel} \omega ~\] 简化为: \[ \tau = I\alpha + 2rp_{\parallel} \omega ~\] 这就是牛顿第二定律的旋转类比。需要注意的是,力矩不一定与角加速度成正比或平行(如预期的那样)。其原因在于粒子的转动惯量可以随时间变化,而对于普通的质量而言,这种情况是不会发生的。
5. 角动量守恒
一般考虑
牛顿第三定律的旋转类比可以写为:“在一个封闭系统中,任何物质上施加的扭矩都无法不对其他物质施加相等且相反的扭矩。” 因此,角动量可以在封闭系统中的物体之间交换,但交换前后的总角动量保持不变(守恒)。
从另一个角度来看,牛顿第一定律的旋转类比可以写为:“刚体在没有外部影响作用下,继续保持匀速旋转状态。” 因此,在没有外部影响的情况下,系统的原始角动量保持不变。
角动量守恒用于分析中心力运动。如果某个物体上的合力始终指向某个中心点,则该物体相对于中心没有扭矩,因为所有力都沿半径向量方向作用,且没有力垂直于半径。数学上,扭矩 \(\boldsymbol{\tau} = \mathbf{r} \times \mathbf{F} = 0\),因为在这种情况下,\(\mathbf{r}\) 和 \(\mathbf{F}\) 是平行向量。因此,物体关于中心的角动量是恒定的。这种情况适用于行星和卫星的引力轨道,其中引力始终指向主要天体,运行物体通过交换距离和速度来保持角动量。中心力运动也用于分析波尔原子模型。
对于行星,角动量分布在行星的自转和轨道革命之间,且这两者常通过各种机制进行交换。地月系统中角动量的守恒导致地球向月球转移角动量,这源于月球对地球施加的潮汐扭矩。这反过来导致地球的自转速率减慢,约为每天 65.7 纳秒,同时月球轨道的半径逐渐增加,约为每年 3.82 厘米。
角动量守恒解释了冰上滑冰者在将手臂和腿靠近垂直旋转轴时的角加速度。通过将身体部分质量靠近轴心,他们减少了身体的转动惯量。由于角动量是转动惯量与角速度的乘积,如果角动量保持不变(守恒),那么滑冰者的角速度(旋转速度)必然增加。
同样的现象导致紧凑星体(如白矮星、中子星和黑洞)在由更大且旋转缓慢的星体形成时,会出现极快的旋转。
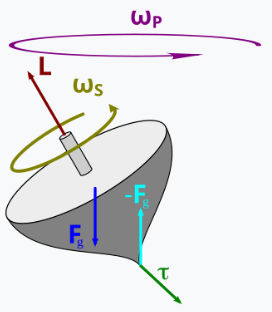
守恒并不总能全面解释系统的动力学,但却是一个关键约束。例如,旋转的陀螺受到重力扭矩的影响,导致其倾斜并改变关于摇动轴的角动量,但如果忽略旋转接触点的摩擦,它关于旋转轴的角动量是守恒的,而关于进动轴的角动量也是如此。此外,在任何行星系统中,行星、恒星、彗星和小行星都可以以许多复杂的方式运动,但仅仅是为了确保系统的角动量得到守恒。
诺特定理表明,每个守恒定律都与底层物理的对称性(不变性)相关。与角动量守恒相关的对称性是旋转不变性。这意味着如果一个系统绕某个轴旋转任意角度,其物理性质不发生改变,从而暗示角动量是守恒的。
与牛顿第二运动定律的关系
虽然角动量的总守恒可以独立于牛顿运动定律理解,视为源于诺特定理在对称于旋转的系统中的表现,但它也可以被简单地理解为一种有效的计算结果的方法,这些结果也可以直接从牛顿第二运动定律及自然力的相关定律(如牛顿第三定律、麦克斯韦方程和洛伦兹力)得出。实际上,给定每个点的初始位置和速度,以及在这种条件下的力,可以使用牛顿第二运动定律计算位置的二阶导数,解出这个方程可以得到关于物理系统随时间发展的全面信息。然而,值得注意的是,在量子力学中,这一情况不再成立,因为存在粒子自旋,这是无法通过空间中点状运动的累积效应来描述的角动量。
作为一个例子,考虑动量惯量的减少,例如当花样滑冰运动员收紧双手时,圆周运动加速。在角动量守恒的情况下,我们有角动量 \( L \)、动量惯量 \( I \) 和角速度 \( \omega \) 的关系: \[ 0 = dL = d(I \cdot \omega) = dI \cdot \omega + I \cdot d\omega~ \] 使用这个关系,我们可以看到变化需要的能量为: \[ dE = d\left(\frac{1}{2} I \cdot \omega^2\right) = \frac{1}{2} dI \cdot \omega^2 + I \cdot \omega \cdot d\omega = -\frac{1}{2} dI \cdot \omega^2~ \] 因此,动量惯量的减少需要投入能量。
这可以与使用牛顿定律计算的功进行比较。旋转体中的每个点在每个时刻都在加速,其径向加速度为: \[ -r \cdot \omega^2~ \] 让我们观察一个质量为 \( m \) 的点,其相对于运动中心的位置向量在某个时刻垂直于 z 轴,且距离为 z。作用在这个点上的向心力,用于保持圆周运动为: \[ -m \cdot z \cdot \omega^2~ \] 因此,将这个点移动到距离运动中心更远的距离 \( dz \) 所需的功为: \[ dW = -m \cdot z \cdot \omega^2 \cdot dz = -m \cdot \omega^2 \cdot d\left(\frac{1}{2} z^2\right)~ \] 对于非点状物体,必须在此基础上进行积分,用单位 z 的质量密度替换 \( m \)。这给出: \[ dW = -\frac{1}{2} dI \cdot \omega^2~ \] 这正是保持角动量守恒所需的能量。
注意,上述计算也可以仅通过运动学按质量进行。因此,滑冰者在收手时加速切向速度的现象可以用通俗的语言理解如下:滑冰者的手掌并不是沿直线移动,因此它们不断向内加速,但由于向内移动的速度始终为零,所以不会获得额外的速度。然而,当手掌靠近身体时情况有所不同:由于旋转产生的加速度现在会增加速度;但由于旋转,速度的增加并不会转化为显著的向内速度,而是导致旋转速度的增加。
静止作用原理
在经典力学中,可以证明作用泛函的旋转不变性意味着角动量守恒。作用在经典物理中定义为位置的泛函,通常用方括号表示 \( x_{i}(t) \),以及初始时间和最终时间。它在笛卡尔坐标系中假设如下形式: \[ S\left([x_{i}];t_{1},t_{2}\right) \equiv \int_{t_{1}}^{t_{2}} dt \left({\frac {1}{2}}m {\frac {dx_{i}}{dt}} {\frac {dx_{i}}{dt}} - V(x_{i})\right)~ \] 其中重复的指标表示对该指标求和。如果作用在一个无穷小变换下是不变的,可以数学地表示为: \[ \delta S = S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right) - S\left([x_{i}];t_{1},t_{2}\right) = 0~ \] 在变换 \( x_{i} \rightarrow x_{i} + \delta x_{i} \) 下,作用变为: \[ S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right) = \int_{t_{1}}^{t_{2}} dt \left({\frac {1}{2}}m {\frac {d(x_{i}+\delta x_{i})}{dt}} {\frac {d(x_{i}+\delta x_{i})}{dt}} - V(x_{i}+\delta x_{i})\right)~ \] 在这里,我们可以对各项进行展开,直到一阶项 \( \delta x_{i} \): \[ \begin{aligned} \frac{d(x_{i}+\delta x_{i})}{dt}\frac{d(x_{i}+\delta x_{i})}{dt} & \simeq \frac{dx_{i}}{dt}\frac{dx_{i}}{dt} - 2\frac{d^{2}x_{i}}{dt^{2}}\delta x_{i} + 2\frac{d}{dt}\left(\delta x_{i}\frac{dx_{i}}{dt}\right) \\ V(x_{i}+\delta x_{i}) & \simeq V(x_{i}) + \delta x_{i}\frac{\partial V}{\partial x_{i}} \end{aligned}~ \] 这给出了作用量的变化: \[ S[x_{i}+\delta x_{i}] \simeq S[x_{i}] + \int_{t_{1}}^{t_{2}}dt\,\delta x_{i}\left(-\frac{\partial V}{\partial x_{i}} - m\frac{d^{2}x_{i}}{dt^{2}}\right) + m\int_{t_{1}}^{t_{2}}dt\frac{d}{dt}\left(\delta x_{i}\frac{dx_{i}}{dt}\right).~ \] 由于所有旋转都可以表示为斜对称矩阵的矩阵指数,即 \(R({\hat {n}},\theta) = e^{M\theta}\) 其中 \(M\) 是一个斜对称矩阵,\(\theta\) 是旋转角度,我们可以将旋转引起的坐标变化 \(R({\hat {n}},\delta \theta)\) 表达为: \[ \delta x_{i} = M_{ij}x_{j}\delta \theta.~ \] 结合运动方程和作用的旋转不变性,我们从上述方程得到: \[ 0 = \delta S = \int_{t_{1}}^{t_{2}}dt\,\frac{d}{dt}\left(m\frac{dx_{i}}{dt}\delta x_{i}\right) = M_{ij}\,\delta \theta \,m\,x_{j}\frac{dx_{i}}{dt}\Bigg|_{t_{1}}^{t_{2}}~ \] 由于这一关系对任何满足 \(M_{ij} = -M_{ji}\) 的矩阵 \(M_{ij}\) 都成立,因此得出以下量的守恒: \[ \ell_{ij}(t) := m\left(x_{i}\frac{dx_{j}}{dt} - x_{j}\frac{dx_{i}}{dt}\right),~ \] 并且有 \(\ell_{ij}(t_{1}) = \ell_{ij}(t_{2})\).这对应于在运动过程中角动量的守恒。
拉格朗日形式
在拉格朗日力学中,围绕给定轴的角动量是该轴上角度广义坐标的共轭动量。例如,围绕 z 轴的角动量 \(L_{z}\) 为: \[ L_{z} = \frac{\partial {\cal L}}{\partial {\dot{\theta}}_{z}}~ \] 其中 \({\cal L}\) 是拉格朗日量,\(\theta_{z}\) 是围绕 z 轴的角度。
注意到 \(\dot{\theta}_{z}\) 是角度的时间导数,即角速度 \(\omega_{z}\)。通常,拉格朗日量通过动能依赖于角速度:动能可以通过将速度分解为径向和切向部分来表示,其中在 x-y 平面围绕 z 轴的切向部分为: \[ \sum_{i}{\frac{1}{2}}m_{i}{v_{T}}_{i}^{2} = \sum_{i}{\frac{1}{2}}m_{i}\left(x_{i}^{2}+y_{i}^{2}\right){{\omega_{z}}_{i}}^{2}~ \] 其中下标 \(i\) 代表第 \(i\) 个物体,\(m\)、\(v_{T}\) 和 \(\omega_{z}\) 分别表示质量、围绕 z 轴的切向速度和该轴的角速度。
对于一个不是点状的物体,其密度为 \(\rho\),我们有: \[ \frac{1}{2}\int \rho (x,y,z)\left(x_{i}^{2}+y_{i}^{2}\right){{\omega_{z}}_{i}}^{2}\,dx\,dy = \frac{1}{2}{I_{z}}_{i}{{\omega_{z}}_{i}}^{2}~ \] 其中积分遍历物体的面积,\(I_{z}\) 是围绕 z 轴的转动惯量。
因此,假设势能不依赖于 \(\omega_{z}\)(这一假设对于电磁系统可能不成立),我们得到第 \(i\) 个物体的角动量: \[ \begin{aligned} {L_{z}}_{i} &= {\frac {\partial {\cal L}}{\partial {{\omega_{z}}_{i}}}} = {\frac {\partial E_{k}}{\partial {{\omega_{z}}_{i}}}} \\ &= {I_{z}}_{i} \cdot {\omega_{z}}_{i} \end{aligned}~ \] 到目前为止,我们已将每个物体旋转了一个单独的角度;我们还可以定义一个整体角度 \(\theta_{z}\),通过它旋转整个系统,从而也使每个物体围绕 z 轴旋转,并得到整体角动量: \[ L_{z} = \sum_{i}{I_{z}}_{i} \cdot {\omega_{z}}_{i}~ \] 然后从欧拉–拉格朗日方程可以得出: \[ 0 = \frac{\partial {\cal L}}{\partial {{\theta_{z}}_{i}}} - \frac{d}{dt}\left(\frac{\partial {\cal L}}{\partial {{{\dot{\theta}}_{z}}_{i}}}\right) = \frac{\partial {\cal L}}{\partial {{\theta_{z}}_{i}}} - \frac{d{L_{z}}_{i}}{dt}~ \] 由于拉格朗日量仅通过势能依赖于物体的角度,我们有: \[ \frac{d{L_{z}}_{i}}{dt} = \frac{\partial {\cal L}}{\partial {{\theta_{z}}_{i}}} = -\frac{\partial V}{\partial {{\theta_{z}}_{i}}}~ \] 这就是第 \(i\) 个物体上的扭矩。
假设系统对旋转不变,因此势能与整体角度 \(\theta_z\) 的旋转无关(因此它可能仅通过物体之间的角度差异依赖于角度,形式为 \(V(\theta_{z_i}, \theta_{z_j}) = V(\theta_{z_i} - \theta_{z_j})\))。因此我们得到总角动量: \[ \frac{dL_z}{dt} = -\frac{\partial V}{\partial \theta_z} = 0~ \] 因此,围绕 z 轴的角动量守恒。
这种分析可以对每个轴分别重复,从而得到角动量向量的守恒。然而,三个轴周围的角度不能同时作为广义坐标处理,因为它们并不是独立的;特别是,每个点用两个角度就足以确定其位置。虽然对于刚体,完整描述其状态需要除了三个平移自由度外,还需要三个旋转自由度;但这些不能定义为围绕笛卡尔坐标轴的旋转(参见欧拉角)。这一警告在量子力学中反映为不同角动量算符分量的非平凡对易关系。
哈密顿形式
同样地,在哈密顿力学中,哈密顿量可以描述为角动量的函数。如前所述,第 \(i\) 个物体围绕 z 轴旋转的动能部分为: \[ \frac{1}{2}{I_{z}}_{i}{{\omega_{z}}_{i}}^{2} = \frac{{{L_{z}}_{i}}^{2}}{2{I_{z}}_{i}}~ \] 这类似于能量与 z 轴方向动量的依赖关系:\(\frac{{{p_{z}}_{i}}^{2}}{2m_{i}}\).
哈密顿方程将围绕 z 轴的角度与其共轭动量(即围绕同一轴的角动量)联系起来: \[ \begin{aligned} \frac{d{\theta_{z}}_{i}}{dt} &= \frac{\partial {\cal H}}{\partial {L_{z}}_{i}} = \frac{{L_{z}}_{i}}{{I_{z}}_{i}} \\ \frac{d{L_{z}}_{i}}{dt} &= -\frac{\partial {\cal H}}{\partial {\theta_{z}}_{i}} = -\frac{\partial V}{\partial {\theta_{z}}_{i}}. \end{aligned}~ \] 第一个方程给出: \[ {L_{z}}_{i} = {I_{z}}_{i} \cdot {\dot{\theta_{z}}_{i}} = {I_{z}}_{i} \cdot {\omega_{z}}_{i}~ \] 因此,我们得到与拉格朗日形式相同的结果。
注意,对于将所有轴组合在一起,我们将动能写为: \[ E_{k} = \frac{1}{2} \sum_{i} \frac{|{\bf{p}_{i}}|^{2}}{2m_{i}} = \sum_{i} \left( \frac{{p_{r}}_{i}^{2}}{2m_{i}} + \frac{1}{2} {\bf{L}_{i}}^{\textsf{T}} {I_{i}}^{-1} {\bf{L}_{i}} \right)~ \] 其中 \(p_{r}\) 是径向方向的动量,转动惯量是一个三维矩阵;加粗的字母表示三维向量。
对于点状物体,我们有: \[ E_{k} = \sum_{i} \left( \frac{{p_{r}}_{i}^{2}}{2m_{i}} + \frac{|{\bf{L}_{i}}|^{2}}{2m_{i}{r_{i}}^{2}} \right)~ \] 这种哈密顿量中动能部分的形式在分析中心势问题时非常有用,并且很容易转化为量子力学的框架(例如在氢原子问题中)。
6. 轨道力学中的角动量
虽然在经典力学中,角动量的语言可以被牛顿运动定律所取代,但它在分析中心势中的运动(如太阳系中的行星运动)中特别有用。因此,太阳系中行星的轨道由其能量、角动量和轨道长轴相对于坐标系的角度所定义。
在天体动力学和天体力学中,一个与角动量密切相关的量定义为: \[ \mathbf{h} = \mathbf{r} \times \mathbf{v},~ \] 称为比角动量。注意到:\(\mathbf{L} = m\mathbf{h}\).在轨道力学计算中,质量通常不重要,因为物体的运动由引力决定。系统中的主天体通常远大于任何围绕它运动的物体,因此较小物体对主天体的引力效应可以忽略;主天体保持近似恒定的速度。所有物体的运动都受到主天体引力的相同影响,无论质量如何,因此在相同条件下它们的运动大致相同。
7. 刚体
角动量也是描述旋转刚体(如陀螺仪或岩质行星)时极其有用的概念。对于具有密度函数 \(\rho(\mathbf{r})\) 的连续质量分布,位于质量内部位置向量为 \(\mathbf{r}\) 的微小体积元 \(dV\) 具有质量元 \(dm = \rho(\mathbf{r})dV\)。因此,该元件的微小角动量为: \[ d\mathbf{L} = \mathbf{r} \times dm \mathbf{v} = \mathbf{r} \times \rho(\mathbf{r})dV \mathbf{v} = dV \mathbf{r} \times \rho(\mathbf{r}) \mathbf{v}~ \] 将这个微小量对整个质量的体积积分,得到其总角动量: \[ \mathbf{L} = \int_{V} dV \mathbf{r} \times \rho(\mathbf{r}) \mathbf{v}~ \] 在接下来的推导中,类似的积分可以替代连续质量情况下的求和。
粒子集合
对于围绕任意原点运动的粒子集合,通过将它们的运动分解为围绕自身质心和围绕原点的分量来推导角动量方程是很有意义的。给定条件为,
- \({\displaystyle m_{i}}\) 是第 \(i\) 个粒子的质量,
- \({\displaystyle \mathbf {R}_{i}}\) 是第 \(i\) 个粒子相对于原点的位置向量,
- \({\displaystyle \mathbf {V}_{i}}\) 是第 \(i\) 个粒子相对于原点的速度向量,
- \({\displaystyle \mathbf {R}}\) 是质心相对于原点的位置向量,
- \({\displaystyle \mathbf {V}}\) 是质心相对于原点的速度向量,
- \({\displaystyle \mathbf {r}_{i}}\) 是第 \(i\) 个粒子相对于质心的位置向量,
- \({\displaystyle \mathbf {v}_{i}}\) 是第 \(i\) 个粒子相对于质心的速度向量。
粒子的总质量就是它们的质量之和, \[ M = \sum_{i} m_{i}.~ \] 质心的位置向量定义为,[30] \[ M \mathbf{R} = \sum_{i} m_{i} \mathbf{R}_{i}.~ \] 观察可得,\(\mathbf{R}_{i} = \mathbf{R} + \mathbf{r}_{i}\) 和 \(\mathbf{V}_{i} = \mathbf{V} + \mathbf{v}_{i}.\)
粒子集合的总角动量是每个粒子角动量的总和。
展开 \(\mathbf{R}_{i}\): \[ \mathbf{L} = \sum_{i} \left[\left(\mathbf{R} + \mathbf{r}_{i}\right) \times m_{i} \mathbf{V}_{i}\right] = \sum_{i} \left[\mathbf{R} \times m_{i} \mathbf{V}_{i} + \mathbf{r}_{i} \times m_{i} \mathbf{V}_{i}\right]~ \] 展开 \(\mathbf{V}_{i}\): \[ \mathbf{L} = \sum_{i} \left[\mathbf{R} \times m_{i} \left(\mathbf{V} + \mathbf{v}_{i}\right) + \mathbf{r}_{i} \times m_{i} \left(\mathbf{V} + \mathbf{v}_{i}\right)\right]~ \] \[ = \sum_{i} \left[\mathbf{R} \times m_{i} \mathbf{V} + \mathbf{R} \times m_{i} \mathbf{v}_{i} + \mathbf{r}_{i} \times m_{i} \mathbf{V} + \mathbf{r}_{i} \times m_{i} \mathbf{v}_{i}\right]~ \] \[ = \sum_{i} \mathbf{R} \times m_{i} \mathbf{V} + \sum_{i} \mathbf{R} \times m_{i} \mathbf{v}_{i} + \sum_{i} \mathbf{r}_{i} \times m_{i} \mathbf{V} + \sum_{i} \mathbf{r}_{i} \times m_{i} \mathbf{v}_{i}.~ \] 可以证明(见下式。)
证明:\(\sum _{i} m_{i} \mathbf{r}_{i} = \mathbf{0}\)
\(\sum _{i}m_{i}\mathbf {r}_{i}=\mathbf{0}\) 和 \(\sum _{i}m_{i}\mathbf {v}_{i}=\mathbf{0},\)
因此,第二项和第三项消失, \[ \mathbf{L} = \sum_{i} \mathbf{R} \times m_{i} \mathbf{V} + \sum_{i} \mathbf{r}_{i} \times m_{i} \mathbf{v}_{i}.~ \] 第一项可以重新排列为, \[ \sum _{i} \mathbf{R} \times m_{i} \mathbf{V} = \mathbf{R} \times \sum _{i} m_{i} \mathbf{V} = \mathbf{R} \times M \mathbf{V},~ \] 因此,粒子集合的总角动量最终为,[31]”
第一项是质心相对于原点的角动量,类似于下文的‘单个粒子’部分,它是一个质量为 \( M \) 的粒子在质心处以速度 \( V \) 运动的角动量。第二项是粒子相对于质心的角动量,类似于下文的‘固定质心’部分。结果是通用的——粒子的运动不局限于围绕原点或质心的旋转或公转。粒子不必是独立的质量点,而可以是连续分布的元素,如刚体。
通过向量恒等式重新排列方程(2),将两项都乘以 “1”,并适当分组后,得到
单粒子情况
在单个粒子围绕任意原点运动的情况下, \[ \begin{aligned} \mathbf{r}_{i} &= \mathbf{v}_{i} = \mathbf{0}, \\ \mathbf{r} &= \mathbf{R}, \\ \mathbf{v} &= \mathbf{V}, \\ m &= M, \end{aligned}~ \] \[ \sum_{i} \mathbf{r}_{i} \times m_{i} \mathbf{v}_{i} = \mathbf{0},~ \] \[ \sum_{i} I_{i} \boldsymbol{\omega}_{i} = \mathbf{0},~ \] 此时总角动量的方程(2)和(3)简化为: \[ \mathbf{L} = \mathbf{R} \times m \mathbf{V} = I_{R} \boldsymbol{\omega}_{R}.~ \] 固定质心情况
在质心相对于原点固定不动的情况下, \[ \mathbf{V} = \mathbf{0},~ \] \[ \mathbf{R} \times M \mathbf{V} = \mathbf{0},~ \] \[ I_{R} \boldsymbol{\omega}_{R} = \mathbf{0},~ \] 此时总角动量的方程(2)和(3)简化为: \[ \mathbf{L} = \sum_{i} \mathbf{r}_{i} \times m_{i} \mathbf{v}_{i} = \sum_{i} I_{i} \boldsymbol{\omega}_{i}.~ \]
8. 广义相对论中的角动量
在现代(20 世纪)理论物理中,角动量(不包括任何内禀角动量——见下文)采用不同的形式描述,而不是经典的伪向量。在这种形式中,角动量是与旋转不变性相关的二形式 Noether 荷。因此,除非时空具有旋转对称性,否则在一般弯曲时空中角动量通常不会局部守恒;而从全局来看,角动量的概念仅在时空渐进平坦的情况下才有意义。如果时空仅具有轴对称性(如 Kerr 度规),则总角动量不守恒,但 \( p_{\phi} \) 是守恒的,这与绕对称轴旋转的不变性有关,其中 \(p_{\phi} = g_{\mu \phi} p^{\phi} = m g_{\mu \phi} dX^{\mu}/d\tau\) 其中 \( g_{\mu \nu} \) 是度规,\( m = \sqrt{|p_{\mu} p^{\mu}|} \) 是静止质量,\( dX^{\mu}/d\tau \) 是四维速度,而 \( X^{\mu} = (t, r, \theta, \phi) \) 是球坐标中的四维位置。
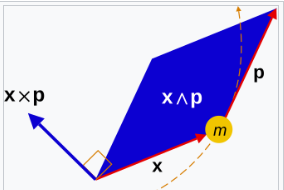
在经典力学中,粒子的角动量可以被重新解释为一个平面元: \[ \mathbf{L} = \mathbf{r} \wedge \mathbf{p}.~ \] 其中外积(∧)取代了叉积(×)(这两种乘积具有相似特性,但并不等同)。这种表示的优势在于,它使用向量 \( x \) 和 \( p \) 来定义平面元,使得几何解释更加清晰,并且该表达式在任意维度中都成立。在笛卡尔坐标系下:
在相对论力学中,粒子的相对论角动量表示为一个二阶反对称张量: \[ M_{\alpha \beta} = X_{\alpha} P_{\beta} - X_{\beta} P_{\alpha} ~ \] 其中使用了四维向量,即四维位置 \( X \) 和四维动量 \( P \),并且将上面的 \( L \) 与质量矩结合在一起,即粒子的相对论质量与其质心的乘积。这可以视为描述质心的运动,因为质量能量是守恒的。
在上述每种情况下,对于一个粒子系统,总角动量就是各个粒子角动量的总和,质心则对应于该系统的质心。
9. 量子力学中的角动量
在量子力学中,角动量(如同其他量一样)被表示为一个算符,其一维投影具有量子化的特征值。角动量服从海森堡不确定性原理,这意味着在任意时刻,只有一个投影(也称为 “分量”)可以被精确测量,其他两个则保持不确定性。因此,量子粒子的旋转轴是未定义的。量子粒子确实具有一种称为 “自旋” 的非轨道角动量,但这种角动量并不对应于旋转运动。在相对论量子力学中,上述的相对论定义成为一个张量算符。
自旋、轨道角动量和总角动量
角动量的经典定义为 \(\mathbf{L} = \mathbf{r} \times \mathbf{p}\) 可以在量子力学中得到延续,通过将 \( \mathbf{r} \) 重新解释为量子位置算符,\( \mathbf{p} \) 重新解释为量子动量算符。此时,\( \mathbf{L} \) 就成为一个算符,具体称为轨道角动量算符。角动量算符的各分量满足李代数 so(3) 的对易关系。事实上,这些算符正是量子希尔伯特空间上旋转群的无穷小作用。(另见下面关于作为旋转生成元的角动量算符的讨论。)
然而,在量子物理中,还存在另一种类型的角动量,称为自旋角动量,由自旋算符 \( \mathbf{S} \) 表示。自旋常被描绘成粒子围绕某轴自转,但这种描述是误导且不准确的:自旋是粒子的一种内在属性,与任何空间中的运动无关,且与轨道角动量本质上不同。所有基本粒子都具有一个特定的自旋(可能为零),并且几乎所有基本粒子都具有非零自旋。例如,电子的 “自旋为 1/2”(实际意味着 “自旋为 \( \hbar / 2 \)”),光子的 “自旋为 1”(实际意味着 “自旋为 \( \hbar \)”),而 π 介子的自旋为 0[40]。
最后,总角动量 \( \mathbf{J} \) 包含了所有粒子和场的自旋角动量和轨道角动量的总和。(对于单个粒子,有 \( \mathbf{J} = \mathbf{L} + \mathbf{S} \))。角动量守恒适用于 \( \mathbf{J} \),但不适用于 \( \mathbf{L} \) 或 \( \mathbf{S} \);例如,自旋-轨道相互作用允许角动量在 \( \mathbf{L} \) 和 \( \mathbf{S} \) 之间相互转移,而总角动量保持不变。电子和光子的总角动量不一定是整数值,也可以是半整数值。[41]
在分子中,总角动量 \( \mathbf{F} \) 是旋振电(轨道)角动量 \( \mathbf{N} \)、电子自旋角动量 \( \mathbf{S} \) 和核自旋角动量 \( \mathbf{I} \) 的总和。对于电子单重态,旋振电角动量记作 \( \mathbf{J} \) 而不是 \( \mathbf{N} \)。正如范弗莱克所解释的,分子旋振电角动量的分量相对于分子固定轴具有不同的对易关系,与相对于空间固定轴的分量的对易关系不同。
量子化
在量子力学中,角动量是量子化的——也就是说,它不能连续变化,而只能在某些允许值之间以 “量子跃迁” 的方式变化。对于任何系统,测量结果的以下限制适用,其中 \( \hbar \) 是约化普朗克常数,\( \hat{n} \) 是任何欧几里得向量,如 \( x \)、\( y \) 或 \( z \):
约化普朗克常数 \( \hbar \) 按日常标准来看非常小,约为 \( 10^{-34} \, \text{J} \cdot \text{s} \),因此这种量子化对宏观物体的角动量没有显著影响。然而,在微观世界中,这一特性非常重要。例如,角动量的量子化对化学中的电子壳层和亚壳层结构有显著影响。
角动量的量子化最早由尼尔斯·玻尔在他的原子模型中提出,随后由埃尔温·薛定谔在他的薛定谔方程中得以预测。
不确定性
在定义 \(\mathbf{L} = \mathbf{r} \times \mathbf{p}\) 中,涉及六个算符:位置算符 \( r_x \)、\( r_y \)、\( r_z \) 和动量算符 \( p_x \)、\( p_y \)、\( p_z \)。然而,海森堡不确定性原理告诉我们,不可能同时以任意精度知道这六个量。因此,关于粒子角动量的可知或可测量性存在限制。结果表明,最好的情况是可以同时测量角动量向量的大小及其沿某一轴的分量。
这种不确定性与角动量算符的不同分量之间不对易密切相关,例如 \( L_x L_y \neq L_y L_x \)。(有关具体的对易关系,请参见角动量算符。
作为旋转生成元的总角动量
如上所述,轨道角动量 \( \mathbf{L} \) 的定义与经典力学中相同:\(\mathbf{L} = \mathbf{r} \times \mathbf{p}\) 但总角动量 \( \mathbf{J} \) 的定义则不同且更基本:\( \mathbf{J} \) 被定义为 “旋转的生成元”。更具体地说,\( \mathbf{J} \) 被定义为使算符 \[ R(\hat{n}, \phi) \equiv \exp\left(-\frac{i}{\hbar} \phi \, \mathbf{J} \cdot \hat{\mathbf{n}}\right)~ \] 成为旋转算符,它将任意系统绕轴 \( \hat{\mathbf{n}} \) 旋转角度 \( \phi \)。(公式中的 "exp" 表示算符的指数函数。)反过来说,不论我们的量子希尔伯特空间是什么,我们期望旋转群 \( \text{SO(3)} \) 会作用在其上。由此便产生了 \( \text{SO(3)} \) 的李代数 \( \text{so(3)} \) 的关联作用;描述 \( \text{so(3)} \) 在我们的希尔伯特空间上作用的算符即为(总)角动量算符。
角动量算符与旋转算符之间的关系与数学中李代数和李群之间的关系相同。角动量与旋转的紧密关系在诺特定理中得到了体现,该定理证明,当物理定律具有旋转不变性时,角动量守恒。
10. 电动力学中的角动量
在描述带电粒子在电磁场中的运动时,由系统的拉格朗日量导出的规范动量 \( \mathbf{P} \) 不是规范不变的。结果,规范角动量 \( \mathbf{L} = \mathbf{r} \times \mathbf{P} \) 也不是规范不变的。相反,物理上有意义的动量,即所谓的动量(在本文中一直使用的),是规范不变的动量,表达式(以 SI 单位表示)为 \[ \mathbf{p} = m \mathbf{v} = \mathbf{P} - e \mathbf{A}~ \] 其中 \( e \) 是粒子的电荷,\( \mathbf{A} \) 是电磁场的磁矢势。规范不变的角动量,即动角动量,给出为 \[ \mathbf{K} = \mathbf{r} \times (\mathbf{P} - e \mathbf{A})~ \] 与量子力学的关系可在关于规范对易关系的文章中进一步讨论。
11. 光学中的角动量
在经典的麦克斯韦电动力学中,坡印廷矢量表示电磁场的线性能量密度。【44】 \[ \mathbf{S} (\mathbf{r}, t) = \epsilon_0 c^2 \mathbf{E} (\mathbf{r}, t) \times \mathbf{B} (\mathbf{r}, t) .~ \] 角动量密度矢量 \( \mathbf{L} (\mathbf{r}, t) \) 的表达与经典力学中的矢量积类似:【45】 \[ \mathbf{L} (\mathbf{r}, t) = \epsilon_0 \mu_0 \mathbf{r} \times \mathbf{S} (\mathbf{r}, t) .~ \] 上述关系在局部(即每个空间点 \( \mathbf{r} \) 的某一时刻 \( t \))都成立。
12. 自然与宇宙中的角动量
热带气旋和其他相关的天气现象涉及角动量守恒以解释其动力学。由于科里奥利效应,气流围绕低压系统缓慢旋转。如果低压增强并且缓慢旋转的空气被吸向中心,为了保持角动量守恒,分子必须加速。当它们到达中心时,速度变得具有破坏性。【2】
约翰内斯·开普勒在不了解动量守恒的情况下推导出了行星运动定律。然而,不久之后,人们发现这些定律可以从角动量守恒中推导出来。行星在椭圆轨道上离太阳越远,运动速度越慢,这可以通过直观的方式解释,因为轨道角动量与轨道半径成正比。由于质量不变且角动量守恒,速度会降低。
潮汐加速是轨道卫星(例如月球)与其主行星(例如地球)之间潮汐力的效应。月球与地球潮汐隆起之间的引力扭矩使月球不断向更高的轨道移动(约每年 3.8 厘米),地球自转减速(−25.858 ± 0.003″/cy²),每天的长度每世纪增加约 1.7 毫秒(其中潮汐效应增加 2.3 毫秒,冰川后反弹减少 0.6 毫秒)。地球失去的角动量转移给月球,以保证整体角动量守恒。
13. 工程与技术中的角动量
利用角动量守恒实现实际优势的例子比比皆是。在蒸汽机或内燃机等发动机中,需要飞轮来有效地将活塞的往复运动转换为旋转运动。
惯性导航系统明确利用了相对于惯性空间角动量守恒的原理。惯性导航使得潜艇能够在极地冰盖下航行,同时也对所有形式的现代导航至关重要。
来复枪子弹利用角动量守恒提供的稳定性,使其飞行轨迹更加准确。来复枪和火炮的发明在战斗中赋予了使用者显著的战略优势,因此成为历史上技术的一个转折点。
14. 历史
艾萨克·牛顿在《自然哲学的数学原理》中,通过对第一运动定律的例子暗示了角动量:
“一个陀螺,其各个部分因凝聚力不断偏离直线运动,但不会停止旋转,除非受到空气的阻力。行星和彗星这样的更大天体在较自由的空间中遇到的阻力较小,因此能够保持其进动和旋转运动更长的时间。”【46】
他在《原理》中没有进一步直接研究角动量,而是写道:
“此类反射有时也会引起物体绕其自身中心的圆周运动。但这些情况在接下来的讨论中不予考虑;如果要证明与此相关的每一个细节将会过于繁琐。”【47】
然而,他关于面积定律的几何证明是牛顿天才的杰出例证,且在中央力的情况下间接证明了角动量守恒。
面积定律
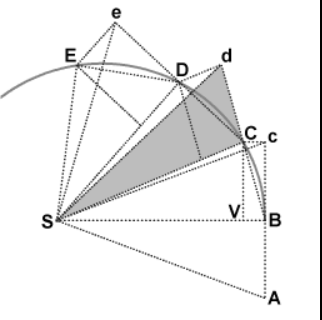
牛顿的推导
当行星绕太阳运行时,太阳与行星之间的连线在相等的时间间隔内扫过相等的面积。这一现象自开普勒阐述其行星运动第二定律以来便已为人所知。牛顿为此推导出了独特的几何证明,并进一步表明太阳引力是所有开普勒定律的成因。
在第一个时间间隔内,物体从点 \( A \) 运动到点 \( B \)。如果不受干扰,它将在第二个时间间隔内继续到达点 \( c \)。当物体到达 \( B \) 时,受到一个朝向 \( S \) 点的冲量。这个冲量赋予它一个指向 \( S \) 的小速度,如果这成为它的唯一速度,它将在第二个时间间隔内从 \( B \) 移动到 \( V \)。根据速度合成规则,这两个速度相加,通过平行四边形 \( BcCV \) 的构造可得出点 \( C \)。因此,物体的路径被冲量偏转,使其在第二个时间间隔结束时到达点 \( C \)。由于三角形 \( SBc \) 和 \( SBC \) 具有相同的底边 \( SB \) 和相同的高度 \( Bc \) 或 \( VC \),它们的面积相同。由于对称性,三角形 \( SBc \) 的面积也等于三角形 \( SAB \) 的面积,因此物体在相等的时间内扫过了相等的面积 \( SAB \) 和 \( SBC \)。
在点 \( C \),物体再次受到朝向 \( S \) 的冲量,在第三个时间间隔内将其路径从 \( d \) 偏转至 \( D \)。因此,物体继续到达 \( E \) 及更远的点,三角形 \( SAB \)、\( SBc \)、\( SBC \)、\( SCd \)、\( SCD \)、\( SDe \)、\( SDE \) 的面积都相同。允许时间间隔无限缩小,路径 \( ABCDE \) 无限接近一条连续曲线。
注意,由于此推导是几何性的,且未施加特定力,因此它证明了比开普勒行星运动第二定律更为普遍的规律。这表明面积定律适用于任何中心力,不论是吸引力还是排斥力,连续或不连续,甚至零力。
面积定律中的角动量守恒
角动量与运动物体扫过面积的比例关系可以通过认识到三角形的底边,即从 \( S \) 到物体的线段,相当于半径 \( r \),而三角形的高与速度的垂直分量 \( v_\perp \) 成比例来理解。因此,如果单位时间内扫过的面积保持不变,则根据三角形面积公式 \(\frac{1}{2} \times (\text{底边}) \times (\text{高})\) 可知,底边与高的乘积(即 \( r v_\perp \) 的乘积)保持不变:如果 \( r \) 和底边长度减少,则 \( v_\perp \) 和高度必须成比例增加。质量保持不变,因此,通过距离和速度的这种交换,角动量 \( r m v_\perp \) 保持守恒。
以三角形 \( SBC \) 为例,其面积等于 \(\frac{1}{2} \times (\text{SB}) \times (\text{VC})\) 无论冲量作用下 \( C \) 最终位于何处,乘积 \( (\text{SB}) \times (\text{VC}) \) 以及 \( r m v_\perp \) 都保持不变。对每个三角形也是如此。
关于任何中心力角动量守恒的另一种面积证明使用了马米孔的扫掠切线定理。【48】【49】
在牛顿之后
莱昂哈德·欧拉、丹尼尔·伯努利和帕特里克·达西都通过对开普勒行星运动第二定律的分析,理解了角动量与面积速度守恒的关系。他们不太可能意识到这对普通旋转物体的影响。
1736 年,欧拉在其《力学》中提到了一些角动量的方程,但并没有进一步发展。
伯努利在 1744 年的一封信中提到 “旋转运动的力矩”,这可能是我们现在理解的角动量的首次概念。
1799 年,皮埃尔-西蒙·拉普拉斯首次意识到固定平面与旋转有关——他称之为不变平面。
1803 年,路易·波瓦松开始将旋转表示为垂直于旋转的线段,并详细阐述了 “力矩守恒”。
在 1852 年,莱昂·傅科在实验中使用陀螺仪展示了地球的自转。
威廉·J·M·兰金在 1858 年的《应用力学手册》中首次以现代意义定义了角动量:
……一条长度与角动量的大小成正比的线,其方向垂直于物体的运动平面和固定点的平面,当从这条线的端点观察物体的运动时,物体的半径向量似乎呈右手旋转。
在 1872 年同一本书的版本中,兰金提到 “角动量一词是由海沃德先生引入的”,可能指的是 R.B.海沃德的文章《一种直接方法来估计关于在空间中以任何方式移动的轴的速度、加速度及所有类似量》,该文章在 1856 年引入,并于 1864 年出版。兰金的说法有误,因为从 18 世纪末到 19 世纪初的许多出版物中都开始使用该术语。然而,海沃德的文章显然是许多英语国家首次使用该术语和概念的文献。在此之前,角动量通常在英语中被称为 “旋转动量”。
15. 另见
- 绝对角动量
- 角动量耦合
- 光的角动量
- 角动量图(量子力学)
- 混沌旋转
- 克莱布施–戈尔丹系数
- 线性-旋转类比
- 量级(角动量
- 保利–鲁班斯基伪向量
- 相对论角动量
- 刚性转子
- 特定相对角动量
- 最优态
16. 参考文献
- “飞碟飞行的空气动力学”。《科学美国人》。2012 年 8 月 9 日。于 2022 年 1 月 4 日检索。
- “热带气旋结构”。国家气象局。于 2022 年 1 月 4 日检索。
- Moore, Thomas (2016). 《塑造物理学的六个思想》,第 C 单元:守恒定律限制相互作用(第三版)。麦 Graw-Hill 教育。第 91 页。ISBN 978-0-07-351394-2。
- 乔治亚州立大学物理与天文学系。“转动惯量:薄盘”。HyperPhysics。于 2023 年 3 月 17 日检索。
- Wilson, E. B. (1915). “线性动量、动能和角动量”。《美国数学月刊》。第 XXII 卷。Ginn and Co.,波士顿,联合芝加哥大学等:第 190 页。
- Worthington, Arthur M. (1906). 《旋转动力学》。Longmans, Green and Co.,伦敦。第 21 页 — 通过 Google 图书。
- Taylor, John R. (2005). 《经典力学》。University Science Books,米尔谷,加州。第 90 页。ISBN 978-1-891389-22-1。
- Dadourian, H. M. (1913). 《物理与工程学生的分析力学》。D. Van Nostrand Company,纽约。第 266 页 — 通过 Google 图书。
- Watson, W. (1912). 《普通物理学》。Longmans, Green and Co.,纽约。第 33 页 — 通过 Google 图书。
- Barker, George F. (1893). 《物理学:高级课程》(第 4 版)。Henry Holt and Company,纽约。第 66 页 — 通过 Google 图书。
- Barker, George F. (1893). 《物理学:高级课程》(第 4 版)。Henry Holt and Company,纽约。第 67–68 页 — 通过 Google 图书。
- Oberg, Erik; 等 (2000). 《机械工程手册》(第 26 版)。Industrial Press, Inc.,纽约。第 143 页。ISBN 978-0-8311-2625-4。
- Watson, W. (1912). 《普通物理学》。Longmans, Green and Co.,纽约。第 34 页 — 通过 Google 图书。
- Kent, William (1916). 《机械工程师口袋书》(第 9 版)。John Wiley and Sons, Inc.,纽约。第 517 页 — 通过 Google 图书。
- Oberg, Erik; 等 (2000). 《机械工程手册》(第 26 版)。Industrial Press, Inc.,纽约。第 146 页。ISBN 978-0-8311-2625-4。
- Oberg, Erik; 等 (2000). 《机械工程手册》(第 26 版)。Industrial Press, Inc.,纽约。第 161–162 页。ISBN 978-0-8311-2625-4。
- Kent, William (1916). 《机械工程师口袋书》(第 9 版)。John Wiley and Sons, Inc.,纽约。第 527 页 — 通过 Google 图书。
- Battin, Richard H. (1999). 《天体动力学的数学与方法简介,修订版》。美国航空航天学会。ISBN 978-1-56347-342-5,第 97 页。
- Rankine, W. J. M. (1872). 《应用力学手册》(第 6 版)。Charles Griffin and Company,伦敦。第 507 页 — 通过 Google 图书。
- Crew, Henry (1908). 《力学原理:为物理和工程学生而作》。Longmans, Green, and Company,纽约。第 88 页 — 通过 Google 图书。
- Worthington, Arthur M. (1906). 《旋转动力学》。Longmans, Green and Co.,伦敦。第 82 页 — 通过 Google 图书。
- Worthington, Arthur M. (1906). 《旋转动力学》。Longmans, Green and Co.,伦敦。第 11 页 — 通过 Google 图书。
- Stephenson, F. R.; Morrison, L. V.; Whitrow, G. J. (1984). "地球自转的长期变化 — 从公元前 700 年到公元 1980 年"。《皇家学会哲学 Transactions》。313 (1524): 47–70。Bibcode:1984RSPTA.313...47S。doi:10.1098/rsta.1984.0082。S2CID 120566848。+2.40 毫秒/世纪,除以 36525 天。
- Dickey, J. O.; 等 (1994). "月球激光测距:阿波罗计划的持续遗产"(PDF)。《科学》。265 (5171): 482–90,见 486。Bibcode:1994Sci...265..482D。doi:10.1126/science.265.5171.482。PMID 17781305。S2CID 10157934。原始文件存档(PDF)于 2022-10-09。
- Landau, L. D.; Lifshitz, E. M. (1995). 《场的经典理论》。理论物理课程。牛津,Butterworth–Heinemann。ISBN 978-0-7506-2768-9。
- Tenenbaum, M.,& Pollard, H. (1985). 《常微分方程:数学、工程与科学的初学者教科书》。
- Ramond, Pierre (2020). 《场论:现代入门》(第 2 版)。Routledge。ISBN 9780429689017。第 1 页摘录。
- David Morin (2008). 《经典力学入门:包括问题和解决方案》。剑桥大学出版社。第 311 页。ISBN 978-1-139-46837-4。第 311 页摘录。
- Battin, Richard H. (1999). 《天体动力学的数学与方法简介,修订版》。美国航空航天学会。第 115 页。ISBN 978-1-56347-342-5。
- Wilson, E. B. (1915). "线性动量、动能和角动量"。《美国数学月刊》。XXII。Ginn and Co.,波士顿,与芝加哥大学等合作:第 188 页,方程(3)。
- Wilson, E. B. (1915). "线性动量、动能和角动量"。《美国数学月刊》。XXII。Ginn and Co.,波士顿,与芝加哥大学等合作:第 191 页,第 8 定理。
- Hawking, S. W.; Ellis, G. F. R. (1973). 《时空的大尺度结构》。剑桥大学出版社。第 62–63 页。doi:10.1017/CBO9780511524646。ISBN 978-0-521-09906-6。
- Misner, C. W.; Thorne, K. S.; Wheeler, J. A. (1973). "20: 4-动量和角动量的守恒定律"。《引力》。W. H. Freeman and Company。
- Synge 和 Schild,《张量微积分》,Dover 出版,1978 年版,第 161 页。ISBN 978-0-486-63612-2。
- de Podesta, Michael (2002). 《理解物质的性质》(第 2 版,插图版,修订版)。CRC Press。第 29 页。ISBN 978-0-415-25788-6。
- R.P. Feynman; R.B. Leighton; M. Sands (1964). 《费曼物理讲义》(第 2 卷)。Addison–Wesley。第 31–37 页。ISBN 978-0-201-02117-2。
- Hall 2013 第 17.3 节
- Veltman, Martinus J G (2018). 《基础粒子物理中的事实与奥秘》(修订版)。世界科学。ISBN 978-981-323-707-0。
- Thaller, Bernd (2005). 《高级视觉量子力学》(插图版)。Springer Science & Business Media。第 114 页。ISBN 978-0-387-27127-9。
- Strange, Paul (1998). 《相对论量子力学:在凝聚态和原子物理中的应用》(插图版)。剑桥大学出版社。第 64 页。ISBN 978-0-521-56583-7。
- Ballantine, K. E.; Donegan, J. F.; Eastham, P. R. (2016). "有多种方式可以旋转光子:总光学角动量的半量化"。《科学进展》。2 (4): e1501748。Bibcode:2016SciA....2E1748B。doi:10.1126/sciadv.1501748。PMC 5565928。PMID 28861467。
- J. H. Van Vleck (1951). "分子中角动量向量的耦合"。《现代物理评论》。23 (3): 213。Bibcode:1951RvMP...23..213V。doi:10.1103/RevModPhys.23.213。
- Littlejohn, Robert (2011). "量子力学中旋转的讲义笔记"(PDF)。物理 221B 2011 年春季。归档(PDF)于 2022-10-09 的原始文件。检索于 2012 年 1 月 13 日。
- Okulov, A Yu (2008). "光子的角动量和相位共轭"。《物理学 B:原子、分子和光学物理》。41 (10): 101001。arXiv:0801.2675。Bibcode:2008JPhB...41j1001O。doi:10.1088/0953-4075/41/10/101001。S2CID 13307937。
- Okulov, A.Y. (2008). "Mandelstam – Brillouin 镜中的光学和声波螺旋结构"。《JETP 信件》(俄文)。88 (8): 561–566。Bibcode:2008JETPL..88..487O。doi:10.1134/s0021364008200046。S2CID 120371573。归档于 2015-12-22 的原始文件。检索于 2015-10-31。
- Newton, Isaac (1803). "公理;或运动定律,定律 I"。《自然哲学的数学原理》。安德鲁·莫特翻译。H. D. Symonds,伦敦。第 322 页 – 通过 Google 图书
- Newton, 公理;或运动定律,推论 III。
- Withers, L. P. (2013). "视觉角动量:Mamikon 与开普勒相遇"。《美国数学月刊》。120 (1): 71–73。doi:10.4169/amer.math.monthly.120.01.071。S2CID 30994835。
- Apostol, Tom M.; Mnatsakanian, Mamikon A. (2012). 《几何的新视野》。MAA 出版社。第 29–30 页。ISBN 978-1-4704-4335-1。
- 见 Borrelli, Arianna (2011). "物理与数学之间的角动量"(PDF)。归档(PDF)于 2022-10-09 的原始文件,提供了关于角动量概念的优秀详细总结。
- Bruce, Ian (2008). "欧拉:力学第 1 卷"。
- "欧拉与丹尼尔·伯努利的通信,伯努利致欧拉,1744 年 2 月 4 日"(PDF)。欧拉档案。归档(PDF)于 2022-10-09 的原始文件。
- Rankine, W. J. M. (1872). 《应用力学手册》(第 6 版)。查尔斯·格里芬公司,伦敦。第 506 页 – 通过 Google 图书。
- Hayward, Robert B. (1864). "一种直接估计速度、加速度及所有类似量的方法,适用于在空间中以任何方式移动的轴及其应用"。《剑桥哲学学会会刊》。10: 1。Bibcode:1864TCaPS..10....1H。
- 例如,见 Gompertz, Benjamin (1818). "关于在两颊之间振动的摆"。《科学与艺术杂志》。III (V): 17 – 通过 Google 图书;Herapath, John (1847). 《数学物理学》。威塔克公司,伦敦。第 56 页 – 通过 Google 图书。
- 例如,见 Landen, John (1785). "关于任何形状物体的旋转运动"。《哲学交易》。LXXV (I): 311–332。doi:10.1098/rstl.1785.0016。S2CID 186212814。
17. 进一步阅读
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2006). 《量子力学》(2 卷)。John Wiley & Sons。ISBN 978-0-471-56952-7。
- Condon, E. U.; Shortley, G. H. (1935). “第三章:角动量”。《原子光谱理论》。剑桥大学出版社。ISBN 978-0-521-09209-8。
- Edmonds, A. R. (1957). 《量子力学中的角动量》。普林斯顿大学出版社。ISBN 978-0-691-07912-7。
- Hall, Brian C. (2013),《数学家的量子理论》,《研究生数学教程》,第 267 卷,Springer。Bibcode:2013qtm..book.....H。ISBN 978-0-387-40122-5。
- Jackson, John David (1998). 《经典电动力学》(第 3 版)。John Wiley & Sons。ISBN 978-0-471-30932-1。
- Serway, Raymond A.; Jewett, John W. (2004). 《科学家和工程师的物理学》(第 6 版)。Brooks/Cole。ISBN 978-0-534-40842-8。
- Thompson, William J. (1994). 《角动量:物理系统旋转对称性的图解指南》。Wiley。ISBN 978-0-471-55264-2。
- Tipler, Paul (2004). 《科学家和工程师的物理学:力学、振荡与波、热力学》(第 5 版)。W. H. Freeman。ISBN 978-0-7167-0809-4。
- Feynman R; Leighton R; Sands M (2013 年 9 月). “19–4 旋转动能”。《费曼物理讲义》(在线版)– 通过费曼讲义网站。