命题与推理(高中)
贡献者: 欄、停敘
在我们的日常生活中,我们总是在做出各种判断和推测。这些判断和推测的基础是什么?它们又是如何得出的?在面对复杂问题时,逻辑能帮助你对事物进行理解,理清思路,做出合理的判断。命题和推理是逻辑思维的基础。命题是我们讨论的对象,是可以判断为真或假的陈述,而推理则是通过一系列合理的步骤,从已知的命题得出新的结论。这种逻辑推理不仅在数学和科学中至关重要,在我们的日常决策中也同样不可或缺。掌握命题和推理的知识,就像拥有了一把打开智慧之门的钥匙,让你在学习和生活中都更加得心应手。
本文将主要介绍原子命题及其相关概念,并深入探讨几种重要的推理过程。虽然这些内容在教材中已经难寻踪迹,但它们是高中数学、其他学科的学习,乃至未来科研探索、日常生活的重要基础。这些知识不仅帮助你认清问题的本质,更为你提供了解决问题的工具。具体点说,面对高考,与其说是在考察每一个具体的知识点,不如说是在假设你已经掌握了所有知识的基础上,去评估你的推理能力和运用熟练度。因此,尽管这些内容看似与高考或数学关系不大,但一旦你能够熟练运用并将其融入日常思维,它们将变得极为重要。
1. 命题
每个领域都有自己的研究对象。研究集合时,研究的对象是集合和元素。研究逻辑时,研究的对象就是命题。
一条可供判断的陈述句被称为命题(proposition),常用大写拉丁字母 $A,B,C$ 等来表示。命题使用真值(truth value)来表示判断的结果。真值用布尔值表示。布尔值有两个,分别为 “真” 和 “假”,分别记作:“${\rm True}$”、“$1$”、“$T$” 和 “${\rm False}$”、“$0$”、“$F$”。
根据命题的判断结果区分,若被判断为真,则称为真命题,判断为假,则称为假命题。一个命题要么为真,要么为假。如果一条陈述句既真又假,或者无法判断真假,则不能称为命题。这种情况出现时,一般是陈述句中的某些概念的定义不清晰。例如:“这个班级中长得好看的人占比 $30\%$” 就不称为命题,因为 “好看的人” 是一个定义不清晰的概念。
不能被分解成更简单部分的命题,称为原子命题(atomic proposition,或基本命题,basic proposition)。例如:“自然数 2 是一个偶数”、“猫在椅子上” 等是原子命题,而 “2 是偶数而且 3 不是偶数”、“如果猫在椅子上,那么猫不在窝里” 就不是原子命题。
如果一个命题包含变量,则称为开放命题(open proposition)。开放命题的真值取决于变量的取值,例如,“自然数 $x$ 是一个偶数” 是一个开放命题,也是一个原子命题。如果 $x=2$,则为真命题;如果 $x=3$,则为假命题。注意,有时限定条件会成为开放命题的变量,比如 “总人口最多的城市是重庆市” 则隐含了空间和时间的限定条件,如果把条件限定在 “2021 年中国” 则是真命题,如果把条件限定在 “2022 年全世界” 则是假命题。
2. *与命题相似、相关的词汇
下面将会介绍一些经常使用的,与命题相似或相关的词汇。他们经常出现,但使用时却极易混淆。
概念、定义
概念(concept)是通过抽象从一群事物中提取出来的,用于反映这些事物共同特性的思维单位。定义(definition)是为了规范某个概念的范围而用语言进行的简要、完整的陈述。通常,描述概念的定义时,会给出概念的内涵或外延:
- 内涵指概念所有特性和关系,反映所指事物的本质属性或特有属性,描述了概念的 “质”、“属性”。
- 外延指所有包括在这个概念中的事物,反映概念的适用范围或具体对象,描述了概念的 “量”、“范围”。
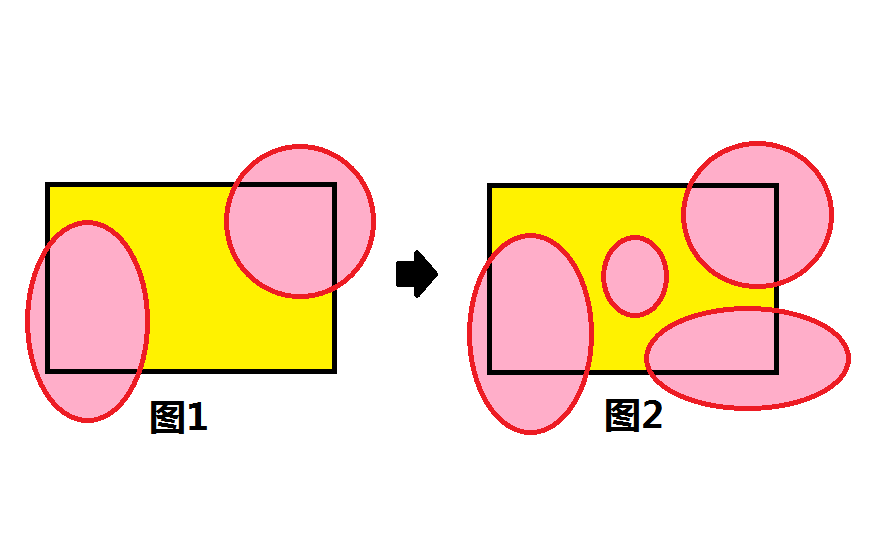
一般说来,一个概念的内涵越丰富,包含的特征越多,其外延就越小;反之,一个概念的内涵越简单,包含的特征越少,其外延就越大。例如,“菱形” 的内涵比 “平行四边形” 更 “多”,但其外延比 “平行四边形” 要 “小”,也就是说 “菱形” 的限定条件比 “平行四边形” 更多,但存在一些 “平行四边形” 不是 “菱形”。也可以借助维恩图来理解内涵与外延的关系,如果用 “黄色” 表示全集,即所有的个体,用 “粉色” 来表示各种性质,那么随着性质的增多,也即条件或要求的增多,个体的数量就越来越少,即 “黄色” 在维恩图上的范围越来越小。
公理、悖论
在某个理论系统中,被视为无需证明的真命题,称为公理(axiom)。作为系统的基本假设,它们是逻辑推理和演绎系统的基础,用于推导其他真命题。初中时学习过的欧几里得几何的五条公理就是最早的公理系统。
对于一个理论系统而言,如何选取公理是最重要的事情。公理是整个理论大厦的基石,决定了理论的框架和结构,直接影响了整个理论系统的结论是否可信。一组精心选取的公理不仅能确保理论的严密性和一致性,还能提高其应用的广泛性和实用性。数学领域的进步,往往是由人们对某条公理的质疑和挑战开始,并由数学家对公理进行调整或重建而引发的。在选取公理时,一般有几项原则:
- 公理必须是自洽的,即公理之间不能相互矛盾。
- 公理应尽可能简洁明了,减少使用概念的数量。
- 公理应具有普遍性和广泛适用性,涵盖尽可能多的情况。
- 理想情况下,每一个公理都应该是独立的,即不能通过其他公理推导出来。
当看到公理时,不必将其奉为神明,根据前面的原则去审视他们,或许就能够发现一个不一样的体系。
悖论(paradox)并非命题,而是一条在逻辑推理中出现了表面看上去互相矛盾结论的陈述句,即:既没有办法判定其为真,又没有办法判定其为假的陈述。悖论的出现通常是因为一些隐含假设或定义问题导致的,它蕴涵着深刻的思想,往往揭示了理论体系中的潜在问题和局限性。一般解决悖论的过程,会带来公理、概念上的明晰和变化。
定理、猜想、引理、推论
在数学领域,对进一步研究和应用有深远影响的一些真命题,称为定理(theorem)。定理常常用于构建更多的理论和解决复杂的问题。定理通常会有一个正式的名字,包含条件和结论两部分,并且以明确的数学语言表述。理解和掌握定理及其证明过程,对于数学和学习和研究至关重要。
猜想(conjecture)是基于部分已知信息或观察提出的一种尚未得到真假性结论的命题。猜想在数学中具有重要作用,因为它们往往为进一步的研究和理论发展提供了方向。很多定理在确认成为定理之前,都曾是猜想。
注意,这里所说的 “尚未得到真假性结论” 的命题并不与命题的定义中 “可供判断” 相冲突。命题的要求是 “可供” 判断,至于怎么样才能判断命题的真假则不包含在内。比如,“每一个不小于 6 的偶数都是两个素数的和”,这句话本身是可供判断的,比如只要有人给出一个反例就说明这句话是假的,又或者如果有人证明出来就说明他是真的。但是在当下,这句话我们尚不知道它的真伪。而刚才给出的例子就是著名的 “哥德巴赫猜想”。
有时,证明一个定理的过程太长了,如果证明过程中有一些与证明过程中其他内容关系不大,且可以重复使用的结论,一般会提前作为一个部分先行证明,并在定理的证明过程中作为一个独立的结论使用,这个部分就称为引理(lemma)。而一个比较重要的定理,往往会根据不同情况得到一些更具体的、便于使用的命题,这些命题称为推论(corollary)。
小结
一下子多出了这么多名词,简单概括一下:
- “概念” 是从实体到思维的抽象结果,是在脑海中的认识和理解,“定义” 是对概念的语言描述,可以用来判别一个事物是否属于某个概念,或区分不同概念。定义描述概念时,或者明确其属性,或者确定其范围。
- “公理” 是不需要证明默认是真命题的命题,“悖论” 是一种既真又假的陈述。这两者对数学领域的变迁举足轻重。
- 由部分已知信息提出的命题,就是 “猜想”。如果猜想得证,并且影响深远,一般会称为 “定理”。证明定理之前使用的一些有用的命题会称为 “引理”,证明定理之后推出的针对具体情况的命题称为 “推论”。
3. 推理方法
在我们的学习和生活中,推理是一种不可或缺的思维工具。它帮助我们从已知的信息出发,得出新的结论,解决问题,甚至是探索未知的领域。推理方法有多种形式,但最基础的是:演绎推理、归纳推理和溯因推理。这三种方法是推理的基本形式,其他类型的推理本质上都是这三种方法的形式和风格上的混搭。
接下来,我们将深入探讨这三种主要的推理方法,了解它们各自的特点和应用场景,之后再了解一个数学上常用的方法——反证法和学习上常用的方法——类比推理。通过学习这些推理方法,你将掌握更加灵活的思考方式,为应对学习中的各种挑战提供强有力的工具。在最后,会稍微谈一谈在学习和题目处理时,这些推理方法的启发。
演绎推理:从大原则到具体结论的思考
从一个大原则推导出具体结论的推理过程,就是所谓的演绎推理(deductive reasoning)。演绎推理的厉害之处在于,只要我们的推理方法和前提是对的,那么最终的结论就肯定不会出错。在数学课上,我们经常会使用演绎推理。数学家们通常会先给出一些基础的规则或公理,然后从这些规则出发,逐步推导出更加复杂的结论。这样的推理不仅精确,而且很可靠。
我们来看看一个非常经典的例子——苏格拉底的 “三段论”(syllogism)。这个例子说明了演绎推理是如何运作的:
这个推理非常简单明了,只要大前提和小前提是对的,那么结论就必然正确。
总的来说,演绎推理是一种很有用的思考方式。只要我们确保前提是正确的,就能放心大胆地使用演绎推理去得出可靠的结论,出现错误结论的情况大多是因为没有正确审视前提或没有使用正确的演绎方法。这样的方法不仅能帮助我们在数学上取得成功,还能在生活中做出明智的决定。
归纳推理:从小观察到大结论的思考
你有没有发现,有时候我们通过观察一些小现象,就能推测出一个大概的结论?比如你观察到食堂中,那些清淡口味的菜品通常剩得最多,你归纳出一个结论:大多数学生更喜欢辛辣的口味。这种从具体的、个别的观察出发,得出一般性结论的思考方式,就叫做归纳推理(inductive reasoning)。在我们的日常生活、学习和研究中,总是会看到各种各样的现象:有些是偶然发生的,比如突然下场大雨;有些是反复出现的,比如每天早晨太阳从东边升起。通过仔细观察这些现象,我们可以猜测并总结出很多有趣的结论。
但是,归纳推理有个小 “缺陷”。因为我们看到的现象只是整体的一部分,所以得出的结论不一定总是准确的。比如,你可能注意到每次寒假你的朋友都会待在家里,于是你猜测,“他寒假都会在家”。但也许有一年他突然决定去旅行了呢?所以,归纳推理虽然有帮助,但它的结论并不是百分百可靠的。
有些人因此对归纳推理不太信任,觉得它不够可靠,容易出错。但其实,在探索未知领域时,尤其是没有现成答案的时候,归纳推理是非常有用的。它能帮助我们从零开始,找到新的方向和可能性。虽然归纳得出的结论有时候不够精确,但它能给我们提供一个大致的方向,这比完全没有头绪要好得多。事实上,大多数现代 AI,尤其是机器学习和深度学习模型,主要依赖于归纳推理。
所以,虽然归纳推理有时候会让我们走偏,但只要我们清楚它的局限性,并且在得出结论前多加思考,它依然是我们探索世界的一把利器。保持开放的心态,留意各种现象,你会发现,归纳推理在学习和生活中有着非常大的价值。
溯因推理:寻找最佳解释的推理方法
有时候我们看到某个现象后,会开始猜测它背后的原因,这种推理方式叫做溯因推理(abductive reasoning),也可以理解为 “最佳解释的推论”。
溯因推理主要用来处理不确定的猜测,它的过程通常是:
- 观察到一个现象;
- 将这个现象和已知的事实进行比较;
- 提出一个可能的解释,这种解释就是所谓 “推测性假设”;
- 通过测试和收集证据,来验证假设。
溯因推理的核心在于提出假设,而魅力也就在于,它提供了一个 “最佳解释” 的方向。虽然猜测未必总是正确,但它帮助我们找到一个出发点,然后我们可以通过进一步的调查或实验来验证这个猜测的准确性。在 AI 的异常检测、诊断推理和解释生成模型方面主要使用溯因推理。
尽管都是得到一个不太可靠的结果,但溯因推理是试图得到解释现有的现象或结果最可能的原因,而归纳推理则是试图从多个观察中总结出一个规律或趋势,得出一个更广泛的结论。
所以,当你下次看到一个现象并感到好奇时,不妨尝试用溯因推理来做出一个猜测。虽然这个猜测可能需要进一步验证,但它将引导你迈出探索的第一步,帮助你更好地理解事物背后的原因。
还原推理:错误的力量
你有没有听说过一种叫做还原推理(reductive reasoning)的方法?它还有两个更常见的名字,叫做归谬法或反证法。这个方法有点特别,因为它的思路是从反面入手,通过证明某个假设是错误的,来间接证明另一个结论是正确的。
还原推理的逻辑其实很简单:你假设某个结论是错误的,然后看看这种假设会不会导致矛盾或不合理的结果。只要你保证推理的过程是正确的,那么如果最终得出的结果明显不可能或者自相矛盾,就可以得出结论:最初的假设是错误的,所以原本被否定的结论其实是正确的。注意,如果你推出来的结论并不是错误的,而是正确的,则并不能证明你最初的假设一定是正确的,刚开始接触反证法的人,大部分会出现这样的问题。
还原推理在数学证明中非常有用,特别是在一些难以直接证明的情况下。它不仅让我们从另一个角度思考问题,还教会我们如何利用矛盾来寻找真相。反证法在逻辑推理中起到的作用是不可忽视的。
*类比推理:以旧识新,寻找相似的智慧
当学习或解决问题时,我们常常会把新遇到的事物和已经熟悉的东西进行比较,找到他们相似的方面,来理解事物或找到解决方法,这就是类比推理(analogical reasoning)的基本思路:通过找出事物之间的相似性,从而发现结论。
类比推理的核心在于:如果两件事情在某些方面相似,那么它们可能在其他方面也会表现出类似的特征。我们可以利用这个思路,用已经了解的知识去理解或推测我们还不完全明白的事物。
再举个例子,假设你喜欢玩某款复杂的策略游戏,后来你接触到另一款新的策略游戏。你可能会自然而然地想:既然这两个游戏都属于策略类型,那么它们的玩法或规则可能也有相似之处。于是,你可以把之前的游戏经验应用到新游戏中,从而更快地掌握它的玩法。
当然,类比推理并不总是准确的,因为相似性不等于完全相同,即使在某些方面相似,也可能在其他方面有很大差异。但它确实是我们在探索新事物时的一种非常有用的思考工具。它让我们能够从过去的经验中获得启发,找到应对新挑战的办法。我们可以更快地理解新事物,也可以发现一些隐藏的规律。在学习和生活中,掌握类比推理的技巧,将让你更具创造力和适应能力,更轻松地应对和理解未知的事物。
总的来说,类比推理不仅是一种推理方法,更一种学习策略。类比推理帮助我们从已知的经验中寻找线索,从而快速理解新知识。
对于学习数学和处理题目的启发
在学习和处理题目时,掌握各种推理方法不仅能帮助我们更有效地解决问题,还能提高我们的思维灵活性和创造力。下面是一些经验之谈,说明这些推理方法如何在学习和题目处理中发挥作用:
- 在解题时,理解并掌握基本的公式、定理和概念至关重要。做数学题的过程,也就是进行演绎推理的过程。保证自己的基础知识牢固、对题目中的信息理解正确、严格按照逻辑顺序进行推导都是在保证演绎推理不出错。学习和应用时,注意定理、推论、条件应用的范围准确是演绎推理的第一要求。
- 在处理陌生领域、方向不甚清晰的问题,尤其是与自然数相关的题目(如:数列、找规律等)时,先举出一些例子,然后通过归纳来猜想出大概的方向,往往让我们在面对新问题时,能迅速找出关键点,归纳出可能的解决方案。
- 当你在解题中条件可能的指向太多,可以通过溯因推理反推出导致最终结果的条件或原因。这种方法在解决复杂问题时特别有用,尤其是在没有明确解题思路的情况下。通过反向思考,你可以推测出可能的解题路径,然后逐步验证,找到正确答案。
- 在数学证明中,反证法非常常用,特别是当直接证明一个结论较为困难时。反证法教会我们在面对问题时,可以换个角度,从相反的方向入手,从而揭示真相。
- 在学习新知识或解决新问题时,类比推理是一种非常有效的策略。它帮助我们利用已有的经验和知识,快速理解新概念或找到新问题的解答路径。