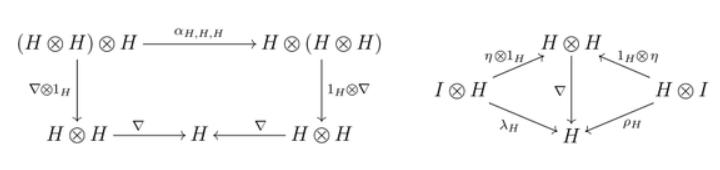霍普夫代数(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章
在数学中,霍普夫代数(Hopf algebra,以海因茨·霍普夫 Heinz Hopf 命名)是一种结构,它既是一个(含幺结合的)代数,又是一个(含余元的余结合)余代数;这些结构的相容性使它成为一个双代数,此外它还配备了一个满足特定性质的反同态。霍普夫代数的表示论尤其优美,因为兼容的余乘法、余元以及反元的存在,使得能够构造表示的张量积、平凡表示以及对偶表示。
霍普夫代数自然地出现在代数拓扑中(其起源之处,并与 H-空间概念相关)、群概形理论、群论(通过群环的概念),以及许多其他地方,因此可能是最常见的一类双代数。霍普夫代数也作为独立的研究对象受到关注,一方面有许多关于具体类实例的研究,另一方面也存在分类问题。它们拥有广泛的应用,从凝聚态物理与量子场论,到弦论以及大型强子对撞机(LHC)现象学。
1. 形式定义
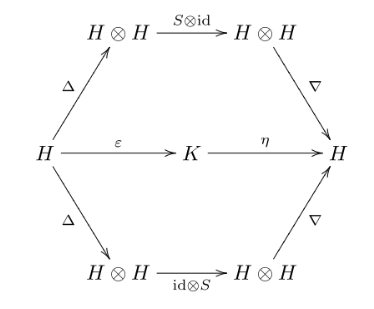
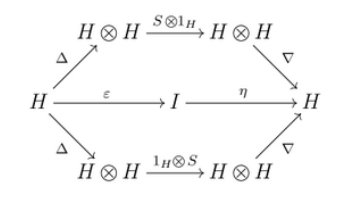
形式上,霍普夫代数是域 $K$ 上的一个(结合且余结合的)双代数 $H$,并配备一个 $K$-线性映射 $S: H \to H$(称为反元,antipode),使得下列图表交换:
这里,$\Delta$ 是双代数的余乘法,$\nabla$ 是其乘法,$\eta$ 是其单位元映射,$\varepsilon$ 是其余元映射。在无求和的 Sweedler 记号下,这一性质也可以表述为: $$ S(c_{(1)})c_{(2)} \;=\; c_{(1)}S(c_{(2)}) \;=\; \varepsilon(c)\,1 \qquad \text{对于所有 } c \in H.~ $$ 与代数的情况类似,在上述定义中,可以将底层的域 $K$ 替换为交换环 $R$。\(^\text{[4]}\)
霍普夫代数的定义是自对偶的(这在上面图表的对称性中有所体现),因此如果可以定义 $H$ 的对偶(当 $H$ 是有限维时总是可能的),那么该对偶也自动是一个霍普夫代数。\(^\text{[5]}\)
结构常数
在固定了底层向量空间的一组基 $\{ e_k \}$ 之后,可以通过乘法的结构常数来定义代数: $$ e_i \nabla e_j = \sum_k \mu_{ij}^k e_k~ $$ 对于余乘法: $$ \Delta e_i = \sum_{j,k} \nu_i^{\,jk} \, e_j \otimes e_k~ $$ 以及反元: $$ S e_i = \sum_j \tau_i^{\,j} e_j~ $$ 结合律要求: $$ \mu_{ij}^k \, \mu_{kn}^m \;=\; \mu_{jn}^k \, \mu_{ik}^m~ $$ 而余结合律要求: $$ \nu_k^{\,ij} \, \nu_i^{\,mn} \;=\; \nu_k^{\,mi} \, \nu_i^{\,nj}~ $$ 连接公理要求: $$ \nu_k^{\,ij} \, \tau_j^{\,m} \, \mu_{im}^n \;=\; \nu_k^{\,jm} \, \tau_j^{\,i} \, \mu_{im}^n~ $$
反元的性质
反元 $S$ 有时被要求具有一个 $K$-线性逆映射,这在有限维情形下会自动成立【需要澄清】,或者当 $H$ 是交换的、余交换的(或更一般地是拟三角的 quasitriangular)时也成立。
一般而言,$S$ 是一个反同态 \(^\text{[6]}\),因此 $S^2$ 是同态;若 $S$ 可逆(通常要求如此),那么 $S^2$ 就是一个自同构。
若 $S^2 = \mathrm{id}_H$,则称该霍普夫代数为对合的,其底层带对合的代数是一个 $*$-代数。若 $H$ 是有限维、在零特征域上半单、交换或余交换的,那么它是对合的。
如果一个双代数 $B$ 承认一个反元 $S$,那么这个 $S$ 是唯一的(“一个双代数至多承认一个霍普夫代数结构”)\(^\text{[7]}\)。因此,反元并不是可以随意选择的额外结构:作为霍普夫代数,是双代数的一个性质。
反元可以类比为群上的逆映射,即把元素 $g$ 映射为 $g^{-1}$\(^\text{[8]}\)。
霍普夫子代数
若 $H$ 是一个霍普夫代数,$A$ 是其子代数,则当 $A$ 同时也是 $H$ 的子余代数,并且反元 $S$ 将 $A$ 映射到 $A$ 中时,称 $A$ 为一个霍普夫子代数。换言之,当把 $H$ 的乘法、余乘法、余元和反元限制到 $A$ 上时,$A$ 本身就是一个霍普夫代数(此外还要求 $H$ 的单位元 $1$ 属于 $A$)。Warren Nichols 与 Bettina Zoeller 于 1989 年证明的 **Nichols–Zoeller 自由性定理表明:如果 $H$ 是有限维的,则自然的 $A$-模 $H$ 是有限秩的自由模;这推广了子群的拉格朗日定理 \(^\text{[9]}\)。由此及积分理论推出,半单有限维霍普夫代数的霍普夫子代数自动是半单的。
在霍普夫代数 $H$ 中,若一个霍普夫子代数 $A$ 满足右稳定性条件,即 $\operatorname{ad}_r(h)(A) \subseteq A \quad \text{对所有 } h \in H$,则称 $A$ 在 $H$ 中是右正规的。其中右伴随映射 $\operatorname{ad}_r$ 定义为 $\operatorname{ad}_r(h)(a) = S(h_{(1)})\, a \, h_{(2)}, \quad a \in A, \; h \in H$.类似地,若 $A$ 在左伴随映射 $\operatorname{ad}_l(h)(a) = h_{(1)}\, a \, S(h_{(2)})$ 下稳定,则称 $A$ 在 $H$ 中是左正规的。当反元 $S$ 是双射时,左右正规条件等价,此时称 $A$ 为一个正规霍普夫子代数。
在 $H$ 中的正规霍普夫子代数 $A$ 满足以下条件(作为 $H$ 的子集相等):$H A^{+} = A^{+} H$,其中 $A^{+}$ 表示 $A$ 上余元的核。此正规性条件意味着 $H A^{+}$ 是 $H$ 的一个霍普夫理想(即:它既是余元核中的代数理想,也是余代数的余理想,并且在反元下稳定)。因此,可以得到一个商霍普夫代数 $H / H A^{+}$,以及一个满射 $H \to H / A^{+} H$,其理论与群论中正规子群和商群的理论类似 \(^\text{[10]}\)。
霍普夫整环
设 $R$ 是一个整环,$K$ 是其分式域。若 $H$ 是 $K$ 上的一个霍普夫代数,则 $R$ 上的一个霍普夫整环 $O$ 是 $H$ 的一个整环,且在代数与余代数运算下封闭:特别地,余乘法 $\Delta : O \to O \otimes O$ 成立 \(^\text{[11]}\)。
类群元素
一个类群元素是满足 $\Delta(x) = x \otimes x$ 的非零元素 $x$。类群元素在反元给出的逆元运算下构成一个群 \(^\text{[12]}\)。
一个原始元素 $x$ 则满足:$\Delta(x) = x \otimes 1 + 1 \otimes x$\(^\text{[13][14]}\)。
2. 例子
| 取决于 | 余乘法 | 余元 | 反元 | 交换性 | 余交换性 | 备注 | |
| 群代数 $KG$ | 群 $G$ | $\Delta(g) = g \otimes g \quad \forall g \in G$ | $\varepsilon(g) = 1 \quad \forall g \in G$ | $S(g) = g^{-1} \quad \forall g \in G$ | 当且仅当 $G$ 是阿贝尔群时成立 | 是 | |
| 从有限群到 $K$ 的函数 $f$,$K^G$(带点加与点乘运算) | 有限群 $G$ | $\Delta(f)(x,y) = f(xy)$ | $\varepsilon(f) = f(1_G)$ | $S(f)(x) = f(x^{-1})$ | 是 | 当且仅当 $G$ 是阿贝尔群时成立 | |
| 紧群上的表象函数 | 紧群 $G$ | $\Delta(f)(x,y) = f(xy)$ | $\varepsilon(f) = f(1_G)$ | $S(f)(x) = f(x^{-1})$ | 是 | 当且仅当 $G$ 是阿贝尔群时成立 | 反之,每一个在 $\mathbb{C}$ 上具有有限 Haar 积分的交换的、对合的、约化的霍普夫代数都以这种方式出现,这给出了 Tannaka–Krein 对偶性的一种表述 \(^\text{[15]}\)。 |
| 代数群上的正则函数 | $\Delta(f)(x,y) = f(xy)$ | $\varepsilon(f) = f(1_G)$ | $S(f)(x) = f(x^{-1})$ | 是 | 当且仅当 $G$ 是阿贝尔群时成立 | 反之,域上的每一个交换霍普夫代数都以这种方式来自一个群概形,从而给出了范畴之间的一种反等价 \(^\text{[16]}\)。 | |
| 张量代数 $T(V)$ | 向量空间 $V$ | $\Delta(x) = x \otimes 1 + 1 \otimes x, \; x \in V,\; \Delta(1) = 1 \otimes 1$ | $\varepsilon(x) = 0$ | $S(x) = -x \quad \forall x \in T^1(V)$(并推广到更高阶张量幂) | 当且仅当 $\dim(V) = 0,1$ 时成立 | 是 | 对称代数与外代数(它们是张量代数的商)在此余乘法、余元和反元定义下也都是霍普夫代数 |
| 普遍包络代数 $U(\mathfrak{g})$ | 李代数 $\mathfrak{g}$ | $\Delta(x) = x \otimes 1 + 1 \otimes x \quad \forall x \in \mathfrak{g}$(此规则与对易子相容,因此可以唯一地扩展到整个 $U$) | $\varepsilon(x) = 0 \quad \forall x \in \mathfrak{g}$(同样可扩展到 $U$) | $S(x) = -x$ | 当且仅当 $\mathfrak{g}$ 是阿贝尔李代数时成立 | 是 | |
| Sweedler 的霍普夫代数 $H = K[c, x] / (c^2 = 1, \; x^2 = 0, \; xc = -cx)$。 | $K$ 是一个特征不等于 2 的域。 | $\Delta(c) = c \otimes c,\;\; \Delta(x) = c \otimes x + x \otimes 1,\;\; \Delta(1) = 1 \otimes 1$ | $\varepsilon(c) = 1,\;\; \varepsilon(x) = 0$ | $S(c) = c^{-1} = c,\;\; S(x) = -cx$ | 否 | 否 | 其底层向量空间由 $\{1, c, x, cx\}$ 张成,因此维数为 4。这是最小的同时非交换且非余交换的霍普夫代数例子。 |
| 对称函数环 \(^\text{[17]}\) | 以完全齐次对称函数 $h_k \; (k \geq 1)$ 表示 $\Delta(h_k) = 1 \otimes h_k + h_1 \otimes h_{k-1} + \cdots + h_{k-1} \otimes h_1 + h_k \otimes 1$ | $\varepsilon(h_k) = 0$ | $S(h_k) = (-1)^k e_k$ | 是 | 是 |
注意:有限群上的函数可以与群环对应起来,尽管它们更自然地被视为对偶结构——群环由有限个元素的和组成,因此可以通过将函数作用在这些求和元素上,与群上的函数配对。
李群的上同调
李群 $G$ 的上同调代数(在域 $K$ 上)是一个霍普夫代数:乘法由杯积给出;余乘法则由群乘法 $G \times G \to G$ 所诱导: $$ H^{*}(G,K) \;\longrightarrow\; H^{*}(G \times G,K) \;\cong\; H^{*}(G,K) \otimes H^{*}(G,K) .~ $$ 这一观察实际上正是霍普夫代数概念的来源。利用这种结构,霍普夫证明了关于李群上同调代数的一个结构定理。
定理(Hopf)\(^\text{[18]}\) 设 $A$ 是一个有限维、分次交换、分次余交换的霍普夫代数,定义在特征为 0 的域上。那么,作为代数,$A$ 是一个自由外代数,其生成元均为奇次数。
3. 表示论
设 $A$ 是一个霍普夫代数,$M, N$ 是 $A$-模。则 $M \otimes N$ 也是一个 $A$-模,定义为: $$ a (m \otimes n) := \Delta(a)(m \otimes n) = (a_{1} \otimes a_{2})(m \otimes n) = (a_{1}m \otimes a_{2}n),~ $$ 其中 $m \in M, \; n \in N,\; \Delta(a) = (a_1, a_2)$。此外,可以将平凡表示定义为基域 $K$,其作用为: $$ a(m) := \epsilon(a) m, \quad m \in K.~ $$ 最后,还可以定义 $A$ 的对偶表示:若 $M$ 是一个 $A$-模,且 $M^{*}$ 是其对偶空间,则有: $$ (af)(m) := f(S(a)m), ~ $$ 其中 $f \in M^{*}, \; m \in M$。
$\Delta, \epsilon, S$ 三者之间的关系保证了某些自然的向量空间同态实际上是 $A$-模同态。例如:向量空间的自然同构 $M \to M \otimes K$ 与 $M \to K \otimes M$ 同时也是 $A$-模同构;向量空间同态 $M^{*} \otimes M \to K,\; f \otimes m \mapsto f(m)$ 也是 $A$-模同态;但映射 $M \otimes M^{*} \to K$ 并不一定是 $A$-模同态。
4. 相关概念
分次霍普夫代数常用于代数拓扑:它们是 $H$-空间所有同调或上同调群的直和上自然出现的代数结构。
局部紧量子群是霍普夫代数的推广,并携带拓扑结构。李群上所有连续函数所成的代数就是一个局部紧量子群。
拟霍普夫代数是霍普夫代数的推广,其中余结合律只在 “扭曲” 意义下成立。它们被用于研究 Knizhnik–Zamolodchikov 方程 \(^\text{[21]}\)。
乘子霍普夫代数由 Alfons Van Daele 于 1994 年提出 \(^\text{[22]}\),是霍普夫代数的推广:其余乘法是从一个代数(可含幺元,也可无幺元)映射到该代数与自身张量积的乘子代数。
霍普夫群-(余)代数由 V. G. Turaev 于 2000 年提出,也是霍普夫代数的一种推广。
弱霍普夫代数
弱霍普夫代数,又称为量子群胚,是霍普夫代数的推广。与霍普夫代数一样,弱霍普夫代数构成一个自对偶的代数类;即:若 $H$ 是一个(弱)霍普夫代数,则其对偶空间 $H^*$(即 $H$ 上的线性形式空间)也是一个(弱)霍普夫代数,其中的代数–余代数结构由 $H$ 与其余代数–代数结构的自然配对给出。
- 通常,弱霍普夫代数 $H$ 被假设为一个有限维的代数和余代数,带有余积 $\Delta: H \to H \otimes H$ 和余元 $\epsilon: H \to k$,它满足霍普夫代数的所有公理,除了可能存在 $\Delta(1) \neq 1 \otimes 1$ 或 $\epsilon(ab) \neq \epsilon(a)\epsilon(b)$(某些 $a,b \in H$)。取而代之,要求满足以下条件: $$ (\Delta(1)\otimes 1)(1\otimes \Delta(1)) \;=\; (1\otimes \Delta(1))(\Delta(1)\otimes 1) \;=\; (\Delta \otimes \mathrm{Id})\Delta(1),~ $$ $$ \epsilon(abc) \;=\; \sum \epsilon(ab_{(1)}) \, \epsilon(b_{(2)}c) \;=\; \sum \epsilon(ab_{(2)}) \, \epsilon(b_{(1)}c),~ $$ 对所有 $a,b,c \in H$ 成立。
- 此外,$H$ 拥有一个弱化的反元 $S: H \to H$,它满足以下公理:
1.$S(a_{(1)})a_{(2)} = 1_{(1)} \, \epsilon(a1_{(2)}), \quad \forall a \in H$(右侧是一个投影,通常记作 $\Pi_R(a)$ 或 $\epsilon_s(a)$,其像是一个称为 $H_R$ 或 $H_s$ 的可分子代数);
2.$a_{(1)} S(a_{(2)}) = \epsilon(1_{(1)}a) \, 1_{(2)}, \quad \forall a \in H$(这是另一个投影,通常记作 $\Pi_L(a)$ 或 $\epsilon_t(a)$,其像是一个可分代数 $H_L$ 或 $H_t$,并且通过 $S$ 与 $H_L$ 反同构);
3.$S(a_{(1)})a_{(2)}S(a_{(3)}) = S(a), \quad \forall a \in H$.需要注意的是,如果 $\Delta(1) = 1 \otimes 1$,那么这些条件便化简为霍普夫代数反元的通常两条条件。
这些公理部分上是为了保证 $H$-模范畴是一个刚性单 oidal 范畴。其中的单位 $H$-模就是上文提到的可分代数 $H_L$。
例如,有限群胚代数就是一个弱霍普夫代数。特别地,集合 $[n]$ 上的群胚代数,若在其中每对元素 $i, j \in [n]$ 之间都有一对可逆箭头 $e_{ij}$ 与 $e_{ji}$,则它同构于 $n \times n$ 矩阵代数 $H$。在这个特殊的 $H$ 上,其弱霍普夫代数结构由下式给出:余积:$\Delta(e_{ij}) = e_{ij} \otimes e_{ij}$,余元:$\epsilon(e_{ij}) = 1$,反元:$S(e_{ij}) = e_{ji}$。 在此情形下,可分子代数 $H_L$ 与 $H_R$ 重合,并且它们是非中心的交换代数(即对角矩阵的子代数)。
关于弱霍普夫代数的早期理论性贡献,可以参见 \(^\text{[23]}\) 和 \(^\text{[24]}\)。
霍普夫代数胚
- 参见 Hopf algebroid。
与群的类比
群可以通过与霍普夫代数相同的图表(或等价地,相同的运算)来公理化,只是此时 $G$ 被视为一个集合而非模。在这种情况下:
- 域 $K$ 被替换为一个单点集;
- 存在一个自然的余元(映射到单点);
- 存在一个自然的余乘法(对角映射);
- 单位元是群的单位元;
- 乘法就是群的乘法;
- 反元就是群的逆元。
从这个角度来看,可以把群看作是定义在 “一元域” 上的一个霍普夫代数 \(^\text{[25]}\)。
5. 编织单 oidal 范畴中的霍普夫代数
霍普夫代数的定义可以自然推广到任意编织单 oidal 范畴 \(^\text{[26][27]}\)。在这样一个范畴 $(C, \otimes, I, \alpha, \lambda, \rho, \gamma)$ 中,一个霍普夫代数是一个六元组 $(H, \nabla, \eta, \Delta, \varepsilon, S)$,其中 $H$ 是 $C$ 中的一个对象,并且:
$\nabla : H \otimes H \to H$ —— 乘法;
$\eta : I \to H$ —— 单位;
$\Delta : H \to H \otimes H$ —— 余乘法;
$\varepsilon : H \to I$ —— 余元;
$S : H \to H$ —— 反元;
这些都是范畴 $C$ 中的态射,并满足相应的条件。
1)三元组 $(H, \nabla, \eta)$ 是单 oidal 范畴 $(C, \otimes, I,\alpha, \lambda, \rho, \gamma)$ 中的一个幺半群,即下列图表交换 \(^\text{[b]}\):
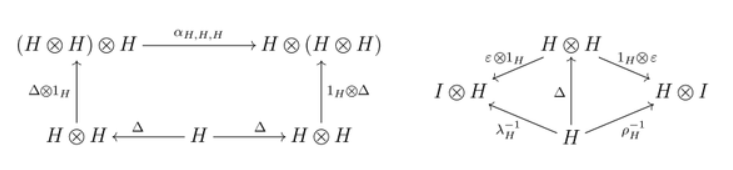
2)三元组 $(H, \Delta, \varepsilon)$ 是单 oidal 范畴 $(C, \otimes, I, \alpha, \lambda, \rho, \gamma)$ 中的一个余幺半群,即下列图表交换 \(^\text{[b]}\):
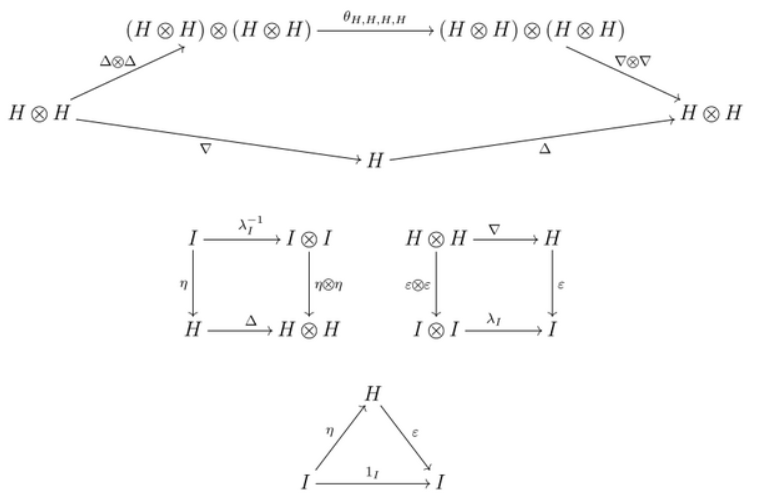
3)在 $H$ 上的幺半群与余幺半群结构是相容的:乘法 $\nabla$ 与单位 $\eta$ 是余幺半群的态射,并且(在这种情形下是等价的)余乘法 $\Delta$ 与余元 $\varepsilon$ 同时也是幺半群的态射;这意味着下列图表必须交换:
其中,$\lambda_{I}: I \otimes I \to I$ 是范畴 $C$ 中的左单位态射,而 $\theta$ 是函子之间的一个自然变换:$(A \otimes B) \otimes (C \otimes D) \;\;\xrightarrow{\;\theta\;}\;\; (A \otimes C) \otimes (B \otimes D)$,它在所有由范畴 $C$ 的结构变换(结合律、左右单位、对换及其逆变换)所构成的自然变换类中是唯一的。
满足 1)、2)、3)性质的五元组 $(H, \nabla, \eta, \Delta,\varepsilon)$ 称为范畴 $(C, \otimes, I, \alpha, \lambda, \rho, \gamma)$ 中的一个双代数。
4)反元的图表是交换的:
典型例子如下:
- 群.在集合范畴 $(\text{Set}, \times, 1)$ 中(其中张量积是笛卡尔积 $\times$,单位对象取为一个任意的单点集,例如 $1=\{\varnothing\}$),三元组 $(H, \nabla, \eta)$ 是范畴意义下的幺半群,当且仅当它是通常代数意义下的幺半群,即运算 $\nabla(x,y) = x \cdot y, \quad \eta(1)$ 的行为与通常的乘法和单位元一致(但元素 $x \in H$ 可能没有逆元)。与此同时,三元组 $(H, \Delta, \varepsilon)$ 是范畴意义下的余幺半群,当且仅当 $\Delta$ 是对角映射:$\Delta(x) = (x,x)$.并且余元 $\varepsilon$ 也能唯一确定:$\varepsilon(x) = \varnothing$。任何这样的余幺半群结构 $(H,\Delta,\varepsilon)$ 都与任意的幺半群结构 $(H,\nabla,\eta)$ 相容,即定义第 3 部分中的图表始终交换。推论:在 $(\text{Set},\times,1)$ 中,每一个幺半群 $(H,\nabla,\eta)$ 自然可以被看作是一个双代数 $(H,\nabla,\eta,\Delta,\varepsilon)$,反之亦然。在这种双代数中,若存在反元 $S:H \to H$,则恰好意味着每个元素 $x \in H$ 在乘法 $\nabla(x,y)=x \cdot y$ 下都有逆元 $x^{-1} \in H$。因此,在集合范畴 $(\text{Set},\times,1)$ 中,霍普夫代数恰好就是通常代数意义下的群。
- 经典霍普夫代数.在特殊情形下,若 $(C,\otimes,s,I)$ 是某个域 $K$ 上的向量空间范畴,那么其中的霍普夫代数正是上述的经典霍普夫代数。
- 群上的函数代数.群上的标准函数代数 $\mathcal{C}(G),\; \mathcal{E}(G),\; \mathcal{O}(G),\; \mathcal{P}(G)$(分别表示连续函数、光滑函数、全纯函数和正则函数)是在 stereotype 空间范畴 $(\text{Ste},\odot)$ 中的霍普夫代数 \(^\text{[28]}\)。
- 群代数.群上的 stereotype 群代数 $\mathcal{C}^{\star}(G),\; \mathcal{E}^{\star}(G),\; \mathcal{O}^{\star}(G),\; \mathcal{P}^{\star}(G)$(分别表示测度、分布、解析泛函与流)是在 stereotype 空间范畴 $(\text{Ste},\circledast)$ 中的霍普夫代数 \(^\text{[28]}\)。这些霍普夫代数被用于非交换群的对偶理论 \(^\text{[29]}\)。
6. 参见
- 拟三角霍普夫代数
- 代数/集合类比
- 霍普夫代数的表示论
- 缎带霍普夫代数
- 超代数
- 超群
- 任意子李代数
- Sweedler 的霍普夫代数
- 置换的霍普夫代数
- Milnor–Moore 定理
7. 注释与参考文献
注释
a.群 $G$ 的有限性意味着 $KG \otimes KG$ 自然同构于 $K[G \times G]$。这被用于上文中的余乘法公式。对于无限群 $G$,$KG \otimes KG$ 是 $K[G \times G]$ 的真子集。在这种情况下,可以赋予有限支撑函数空间一个霍普夫代数结构。
b.这里 $\alpha_{H,H,H} : (H \otimes H) \otimes H \;\to\; H \otimes (H \otimes H)$,$\lambda_H : I \otimes H \;\to\; H$,$
\rho_H : H \otimes I \;\to\; H$ 分别是单 oidal 范畴 $(C, \otimes, I, \alpha, \lambda, \rho, \gamma)$ 中的结合律、左单位和右单位的自然变换。
引文
- Haldane, F. D. M.; Ha, Z. N. C.; Talstra, J. C.; Bernard, D.; Pasquier, V. (1992). *Yangian symmetry of integrable quantum chains with long-range interactions and a new description of states in conformal field theory. Physical Review Letters. 69 (14): 2021–2025. Bibcode:1992PhRvL..69.2021H. doi:10.1103/physrevlett.69.2021. PMID 10046379.
- Plefka, J.; Spill, F.; Torrielli, A. (2006). Hopf algebra structure of the AdS/CFT S-matrix. Physical Review D. 74 (6) 066008. arXiv\:hep-th/0608038. Bibcode:2006PhRvD..74f6008P. doi:10.1103/PhysRevD.74.066008. S2CID 2370323.
- Abreu, Samuel; Britto, Ruth; Duhr, Claude; Gardi, Einan (2017-12-01). Diagrammatic Hopf algebra of cut Feynman integrals: the one-loop case. Journal of High Energy Physics. 2017 (12): 90. arXiv:1704.07931. Bibcode:2017JHEP...12..090A. doi:10.1007/jhep12(2017)090. ISSN 1029-8479. S2CID 54981897.
- Underwood 2011, p. 55
- Underwood 2011, p. 62
- Dăscălescu, Năstăsescu & Raianu (2001). "Prop. 4.2.6". Hopf Algebra: An Introduction. p. 153.
- Dăscălescu, Năstăsescu & Raianu (2001). "Remarks 4.2.3". Hopf Algebra: An Introduction. p. 151.
- Quantum groups lecture notes
- Nichols, Warren D.; Zoeller, M. Bettina (1989). *A Hopf algebra freeness theorem. American Journal of Mathematics, 111 (2): 381–385. doi:10.2307/2374514. JSTOR 2374514. MR 0987762.
- Montgomery 1993, p. 36
- Underwood 2011, p. 82
- Hazewinkel, Michiel; Gubareni, Nadezhda Mikhaĭlovna; Kirichenko, Vladimir V. (2010). *Algebras, Rings, and Modules: Lie Algebras and Hopf Algebras*. Mathematical surveys and monographs. Vol. 168. American Mathematical Society. p. 149. ISBN 978-0-8218-7549-0.
- Mikhalev, Aleksandr Vasilʹevich; Pilz, Günter, eds. (2002). The Concise Handbook of Algebra. Springer-Verlag. p. 307, C.42. ISBN 978-0-7923-7072-7.
- Abe, Eiichi (2004). Hopf Algebras. Cambridge Tracts in Mathematics. Vol. 74. Cambridge University Press. p. 59. ISBN 978-0-521-60489-5.
- Hochschild, G (1965). Structure of Lie groups. Holden-Day, pp. 14–32.
- Jantzen, Jens Carsten (2003). Representations of algebraic groups. Mathematical Surveys and Monographs, vol. 107 (2nd ed.), Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-3527-2. Section 2.3.
- Hazewinkel, Michiel (January 2003). Symmetric Functions, Noncommutative Symmetric Functions, and Quasisymmetric Functions. Acta Applicandae Mathematicae. 75 (1–3): 55–83. arXiv\:math/0410468. doi:10.1023/A:1022323609001. S2CID 189899056.
- Hopf, Heinz (1941). Über die Topologie der Gruppen–Mannigfaltigkeiten und ihre Verallgemeinerungen. Ann. of Math. 2 (in German). 42 (1): 22–52. doi:10.2307/1968985. JSTOR 1968985.
- Underwood 2011, p. 57
- Underwood 2011, p. 36
- Montgomery 1993, p. 203
- Van Daele, Alfons (1994). *Multiplier Hopf algebras* (PDF). Transactions of the American Mathematical Society. 342 (2): 917–932. doi:10.1090/S0002-9947-1994-1220906-5.
- Böhm, Gabriella; Nill, Florian; Szlachanyi, Kornel (1999). Weak Hopf Algebras. J. Algebra. 221 (2): 385–438. arXiv\:math/9805116. doi:10.1006/jabr.1999.7984. S2CID 14889155.
- Nikshych, Dmitri; Vainerman, Leonid (2002). Finite groupoids and their applications. In Montgomery, S.; Schneider, H.-J. (eds.). New directions in Hopf algebras. Vol. 43. Cambridge: M.S.R.I. Publications. pp. 211–262. ISBN 978-0-521-81512-3.
- Group = Hopf algebra, « Secret Blogging Seminar, Group objects and Hopf algebras », video of Simon Willerton.
- Turaev & Virelizier 2017, 6.2.
- Akbarov 2009, p. 482.
- Akbarov 2003, 10.3.
- Akbarov 2009.
参考文献
- Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras. An Introduction, Pure and Applied Mathematics, vol. 235 (1st ed.), Marcel Dekker, ISBN 978-0-8247-0481-0, Zbl 0962.16026.
- Cartier, Pierre (2007), "A Primer of Hopf Algebras", in Cartier, P.; Moussa, P.; Julia, B.; Vanhove, P. (eds.), Frontiers in Number Theory, Physics, and Geometry, vol. II, Berlin: Springer, pp. 537–615, doi:10.1007/978-3-540-30308-4_12, ISBN 978-3-540-30307-7.
- Fuchs, Jürgen (1992), Affine Lie algebras and quantum groups. An introduction with applications in conformal field theory, Cambridge Monographs on Mathematical Physics, Cambridge: Cambridge University Press, ISBN 978-0-521-48412-1, Zbl 0925.17031.
- Heinz Hopf, Über die Topologie der Gruppen-Mannigfaltigkeiten und ihrer Verallgemeinerungen, Annals of Mathematics 42 (1941), 22–52. Reprinted in Selecta Heinz Hopf, pp. 119–151, Springer, Berlin (1964). MR 0004784, Zbl 0025.09303.
- Montgomery, Susan (1993), Hopf algebras and their actions on rings, Regional Conference Series in Mathematics, vol. 82, Providence, Rhode Island: American Mathematical Society, ISBN 978-0-8218-0738-5, Zbl 0793.16029.
- Street, Ross (2007), Quantum groups: A Path To Current Algebra, Australian Mathematical Society Lecture Series, vol. 19, Cambridge University Press, ISBN 978-0-521-69524-4, MR 2294803, Zbl 1117.16031.
- Sweedler, Moss E. (1969), Hopf algebras, Mathematics Lecture Note Series, W. A. Benjamin, Inc., New York, ISBN 978-0-8053-9254-8, MR 0252485, Zbl 0194.32901.
- Underwood, Robert G. (2011), An Introduction to Hopf Algebras, Berlin: Springer-Verlag, ISBN 978-0-387-72765-3, Zbl 1234.16022.
- Turaev, Vladimir; Virelizier, Alexis (2017), Monoidal Categories and Topological Field Theory, Progress in Mathematics, vol. 322, Springer, doi:10.1007/978-3-319-49834-8, ISBN 978-3-319-49833-1.
- Akbarov, S.S. (2003). "Pontryagin duality in the theory of topological vector spaces and in topological algebra". Journal of Mathematical Sciences. 113 (2): 179–349. doi:10.1023/A:1020929201133. S2CID 115297067.
- Akbarov, S.S. (2009). "Holomorphic functions of exponential type and duality for Stein groups with algebraic connected component of identity". Journal of Mathematical Sciences. 162 (4): 459–586. arXiv:0806.3205. doi:10.1007/s10958-009-9646-1. S2CID 115153766.