哈尔滨工业大学 2000 年硕士物理考试试题

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

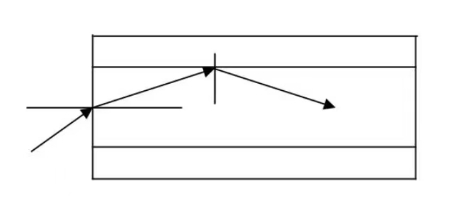
1. 设光纤芯线与外套的折射率 $n_g>n_c$，垂直端面外介质的折射率为 $n_a$(如图 1)，试求能使光在光纤内发生全反射的入射光束的最大孔径角 $i_0$。若将光纤制成圆锥腔，试问有否 “聚光” 作用，并说明理由。
   
   图 1
2. 如图二所示望远镜，物镜 $L_1$ 的焦距 $f_1$，镜框内径 $D_1$;目镜 $L_2$ 的焦距 $f_2$,镜框内径 $D_2$。在重合焦平面上的光阑 $A$ 的孔径为 $d$。试求该望远镜的孔径光阑、入射瞳、出射瞳和视场光阑的位置和大小。又若当你用此望远镜观测时上述量有何不同。
   
   图 2
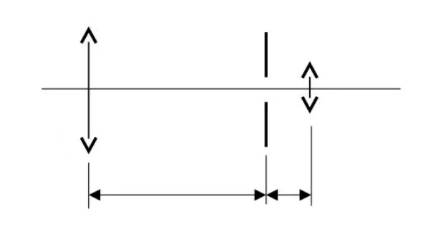
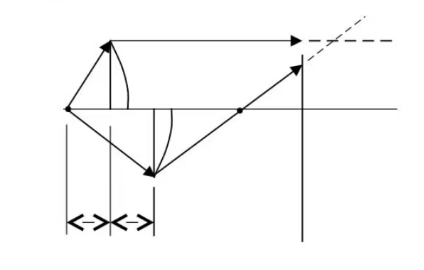
3. 将焦距为的柱透镜沿轴线对半剖开，分成两片半透镜 $L_A$ 和 $L_B$，按图三位置安放。$P$ 点为波长 $\lambda$ 的单色线光源。在两束光交叠区域放置观察屏 $Q$。
   (1)写出明暗条纹的条件;
   (2)指出中央条纹的位置及明或暗;
   (3)讨论若屏 $Q$ 向右移动，条纹为何变化。
   
   图 3
4. 一凹面镜上放一平晶，为图 4 所示，以单色光垂直照射观察干涉现象。当波长 $\lambda_1=500nm$ 时，中心处为暗纹，连续改变波长直至 $\lambda_2=600nm$ 时，中心处才又变为暗纹。
   (1)请定性描述零级条纹的位置及明暗、条纹宽窄、条纹间距和条纹形状;
   (2)计算空气膜的最大厚度。
   
   图 4
5. 一平面透射光栅置于两介质之界面上，光栅常数为 $d$。两介质的折射率 $n_1< n_2$。入射光在 $n_!$ 介质中波长为 $\lambda$，入射角为 $\theta$，照亮光栅的 $N$ 个缝。试求
   (1)光栅零级条纹的衍射角 $\varphi$_0;
   (2)该零级条纹的半角宽度。
6. 两正交尼科耳棱镜之间插一方解石晶片，它的光轴与表面平行，并与尼科耳棱镜的主截面成 45°角。设光通过第一个尼科耳棱镜后的振幅为 1，通过晶片时引起 o 光 e 光的位相差 $\Delta \varphi$。试求
   (1)通过晶片后 o 光和 e 光的振幅和光强;
   (2)通过第二个尼科耳棱镜后光的振幅和光强。
7. 一平薄圆环内外半径为 $R_1$、$R_2$，若以圆环中心为原点，在圆环平面上 $r$ 为矢径。面电荷密度 $\sigma_e=\frac{\sigma}{r}$，其中 $R_1\le r \le R_2$，常量 $\sigma>0$。试求其轴线上距原点 $x$ 处的电场强度。
8. 上题中，若圆环绕轴线以匀角速ω转动，试求轴线上距原点 $x$ 处的磁感应强度。