格林函数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：如果我们已知某个微分方程在点源作用下的解 $G(x, x')$，即满足 $\hat{L}(x)G(x,x') = \delta(x - x')$ 的格林函数，其中 $\hat{L}(x)$ 是一个线性微分算子，那么我们可以通过叠加原理构造出任意源项 $f(x)$ 下的解：$u(x) = \int f(x') G(x, x')\, dx'$ 从而求得方程 $\hat{L}(x) u(x) = f(x)$ 的解。简而言之，如果你知道格林函数，就可以用它通过积分方式表示出任意源函数 $f(x)$ 下的解 $u(x)$。

　　 在数学中，格林函数（Green's function，亦称 Green 函数）是定义在某一给定初始条件或边界条件下的非齐次线性微分算子的冲激响应。

　　 这意味着，如果 $L$ 是一个线性微分算子，那么：

　　 通过叠加原理，对于一个线性常微分方程（ODE）$Ly = f$，可以先对每个源点 $s$ 求解 $LG = \delta_s$，由于源项可以看作多个δ函数的叠加，根据线性算子 $L$ 的线性性，最终的解也是各个格林函数的线性叠加。

　　 格林函数得名于英国数学家乔治·格林，他在 1820 年代首次提出了这一概念。在现代关于线性偏微分方程的研究中，格林函数更多被视为基本解的一种方式来研究。

　　 在多体理论中，这一术语也广泛用于物理学，特别是在量子场论、空气动力学、空气声学、电动力学、地震学和统计场论中，用来表示各种类型的关联函数，即便它们并不总是符合严格的数学定义。在量子场论中，格林函数还扮演着传播子的角色。

1. 定义与用途

　　 格林函数 $G(x, s)$ 是一个线性微分算子 $L = L(x)$ 在欧几里得空间子集 $\mathbb{R}^n$ 上的某个点 $s$ 处作用于分布（广义函数）上的解，它满足以下方程： $$ L\,G(x,s) = \delta(s - x),~ $$ 其中 $\delta$ 是狄拉克 δ 函数。 格林函数的这个性质可以被用来求解如下形式的微分方程： $$ L\,u(x) = f(x).~ $$ 如果算子 $L$ 的核（解空间）非平凡，那么格林函数不唯一。不过在实际中，通过对称性、边界条件或其他外部施加的限制条件，通常可以选定一个唯一的格林函数。格林函数可根据所满足的边界条件类型进行分类，称为 “格林函数编号”。格林函数不一定是实变量意义下的函数，通常是在分布意义下理解的。

　　 格林函数也是求解波动方程和扩散方程的重要工具。在量子力学中，哈密顿算子的格林函数是一个核心概念，与态密度的概念有重要联系。

　　 在物理学中，格林函数的定义通常与上述数学定义符号相反，即满足： $$ L\,G(x, s) = \delta(x - s).~ $$ 由于狄拉克 δ 函数是偶函数，这种符号差异不会对格林函数的基本性质产生实质影响。

　　 如果算子是平移不变的，也就是说当 $L$ 对 $x$ 的系数是常数时，格林函数可以写成卷积核的形式： $$ G(x, s) = G(x - s).~ $$ 在这种情形下，格林函数等同于线性时不变系统理论中的脉冲响应。

2. 动机

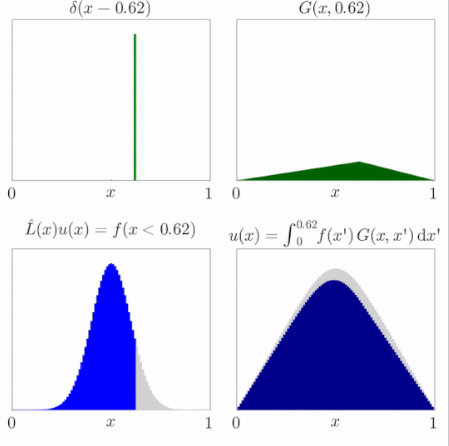
　　 粗略地说，如果对于算子 $L$ 能找到一个函数 $G$ 满足格林函数方程（公式 1），那么将该方程两边乘以 $f(s)$ 并对 $s$ 积分，就得到： $$ \int L G(x, s)\, f(s)\, ds = \int \delta(x - s)\, f(s)\, ds = f(x).~ $$ 因为算子 $L = L(x)$ 是线性的，且仅作用于变量 $x$（而不作用于积分变量 $s$），我们可以将 $L$ 移出积分号，得到： $$ L\left(\int G(x, s)\, f(s)\, ds\right) = f(x).~ $$ 这意味着： $$ u(x) = \int G(x, s)\, f(s)\, ds~ $$ 是微分方程 $Lu(x) = f(x)$ 的一个解。

　　 因此，只要已知公式 1 中的格林函数 $G(x, s)$ 和公式 2 中右侧的源项 $f(x)$，就可以通过公式 3 求得解 $u(x)$。这个过程依赖于算子 $L$ 的线性性质。

　　 换句话说，公式 2 的解 $u(x)$ 可以通过公式 3 的积分表达式来确定。尽管 $f(x)$ 是已知的，但除非 $G$ 也已知，否则这个积分无法实际计算。因此，问题的关键转变为寻找满足公式 1 的格林函数 $G$。因此，格林函数有时也被称为与算子 $L$ 对应的基本解。

　　 并非每一个算子 $L$ 都允许存在格林函数。从另一个角度看，格林函数也可以被视为算子 $L$ 的一个右逆元。除了找到特定算子的格林函数可能具有挑战之外，公式 3 中的积分本身可能也相当难以计算。但这种方法在理论上给出了一个精确解法。

　　 这个过程还可以被理解为：将 $f$ 分解为狄拉克 δ 函数基底的展开（即将 $f$ 投影到 $\delta(x - s)$ 上），并将每个投影对应的解叠加起来。这样的积分方程被称为 Fredholm 积分方程，其研究构成了 Fredholm 理论的基础。

3. 用于求解非齐次边值问题的格林函数

　　 在数学中，格林函数的主要用途是求解非齐次边值问题。在现代理论物理中，格林函数通常也用作费曼图中的传播子；在这种语境下，“格林函数” 一词也常被泛指为**任意的关联函数。

框架

　　 设 $L$ 是一个 Sturm–Liouville 算子，也即如下形式的线性微分算子： $$ L = \frac{d}{dx}\left[p(x)\frac{d}{dx}\right] + q(x)~ $$ 同时设 $\mathbf{D}$ 是一个向量值的边界条件算子，定义为： $$ \mathbf{D}u = \begin{bmatrix} \alpha_1 u'(0) + \beta_1 u(0) \\ \alpha_2 u'(\ell) + \beta_2 u(\ell) \end{bmatrix}~ $$ 设 $f(x)$ 是定义在区间 $[0, \ell]$ 上的连续函数。进一步设定如下边值问题成立： $$ \begin{aligned} Lu &= f \\ \mathbf{D}u &= \mathbf{0} \end{aligned}~ $$ 该问题被称为 “正则的”，即：当 $f(x) = 0$（在所有 $x$ 上恒等于零）时，其唯一解为 $u(x) = 0$。\(^\text{[a]}\)

定理

　　 存在且仅存在一个函数 $u(x)$，满足以下边值问题： $$ \begin{aligned} Lu &= f \\ \mathbf{D}u &= \mathbf{0} \end{aligned}~ $$ 其解可由下式给出： $$ u(x) = \int_0^{\ell} f(s)\, G(x, s)\, ds~ $$ 其中 $G(x, s)$ 是满足以下条件的格林函数：

  1. 连续性：$G(x, s)$ 在变量 $x$ 和 $s$ 上连续。
  2. 齐次性：对于 $x \ne s$，有 $L G(x, s) = 0$
  3. 边界条件：对于 $s \ne 0$，有 $\mathbf{D} G(x, s) = \mathbf{0}$
  4. 导数跳跃条件：$G'(s_0^+, s) - G'(s_0^-, s) = 1/p(s)$
  5. 对称性：$G(x, s) = G(s, x)$

先进格林函数与延迟格林函数

　　 格林函数并不一定是唯一的，因为将任意一个齐次方程的解加到某个格林函数上，所得的函数仍然是一个格林函数。因此，如果齐次方程存在非平凡解，那么将会存在多个不同的格林函数。在某些边值问题或初值问题中，我们需要寻找一种在 $s \leq x$ 时才非零的格林函数，这种情况下得到的解被称为延迟格林函数。类似地，如果格林函数只在 $s \geq x$ 时才非零，它被称为先进格林函数。在这种情形下，任何这两种格林函数的线性组合也是一个有效的格林函数。先进格林函数与延迟格林函数统称为单边格林函数，而在整个定义域 $x$ 上都可能非零的格林函数被称为双边格林函数。在变量 $x$ 表示时间的情形下，“先进” 与 “延迟” 的术语尤为重要。

　　 此时，延迟格林函数所给出的解仅依赖于过去的源项，因此是因果的；而先进格林函数所给出的解则依赖于未来的源项，因此是非因果的。在这类问题中，因果性的延迟格林函数通常具有物理意义。然而，在某些反问题（例如从边界数据反推出源项）中，先进格林函数则是一个有力的工具。在研究非齐次电磁波动方程的解时，先进格林函数与延迟格林函数的使用尤为常见。

4. 求解格林函数

单位分析

　　 虽然单位分析无法唯一确定格林函数的具体形式，但它是通过其他方法求得格林函数后进行合理性检查的重要工具。我们先来看格林函数的定义方程： $$ LG(x, s) = \delta(x - s),~ $$ 这表明格林函数 $G$ 的单位不仅依赖于算子 $L$ 的单位，还依赖于位置向量 $x$ 和 $s$ 所在空间的维度与单位。因此我们可以得到如下单位关系： $$ [[G]] = [[L]]^{-1} [[dx]]^{-1},~ $$

　　 其中 $[[G]]$ 表示格林函数 $G$ 的物理单位，$dx$ 是该空间（或时空）的体积元。

　　 示例 1：时间变量中的二阶微分

　　 若 $L = \partial_t^2$，且时间是唯一变量，则：
$[[L]] = [[\text{time}]]^{-2}$，
$[[dx]] = [[\text{time}]]$，
所以 $[[G]] = [[\text{time}]]$ 即此时格林函数的单位为时间。

　　 示例 2：d'Alembert 算子（波动算子）

　　 若 $L = \Box = \frac{1}{c^2} \partial_t^2 - \nabla^2$，为 d'Alembert 算子，且空间维数为 3，则：
$[[L]] = [[\text{length}]]^{-2}$，（单位为 $\text{m}^{-2}$）
$[[dx]] = [[\text{time}]] [[\text{length}]]^3$，（单位为 $\text{s} \cdot \text{m}^3$）
所以： $$ [[G]] = [[\text{time}]]^{-1} [[\text{length}]]^{-1}.~ $$ 即此时格林函数的单位为 $\text{s}^{-1} \cdot \text{m}^{-1}$。

特征值展开

　　 如果一个微分算子 $L$ 存在一组完备的特征向量 $\Psi_n(x)$（即存在函数 $\Psi_n$ 和标量 $\lambda_n$ 满足 $L \Psi_n = \lambda_n \Psi_n$），那么就可以利用这些特征函数和特征值构造出格林函数。

　　 “完备” 意味着函数集合 $\{\Psi_n\}$ 满足以下完备关系： $$ \delta(x - x') = \sum_{n=0}^{\infty} \Psi_n^{\dagger}(x') \Psi_n(x),~ $$ 其中 $\delta(x - x')$ 是狄拉克δ函数，$\dagger$ 表示复共轭。

　　 于是格林函数可以表示为： $$ G(x, x') = \sum_{n=0}^{\infty} \frac{\Psi_n^{\dagger}(x') \Psi_n(x)}{\lambda_n},~ $$ 这提供了一种将格林函数表示为特征函数与特征值之和的方法。

　　 将算子 $L$ 应用于上述等式的两边，会得到我们预设的完备性关系。

　　 以上形式的格林函数研究，以及其与由特征向量构成的函数空间之间的关系，被称为弗雷德霍姆理论。

　　 除此之外，还有多种方法可以求得格林函数，包括镜像法、变量分离法和拉普拉斯变换等。\(^\text{[8]}\)

关于 Wronskian 的表示

　　 设 $L$ 是定义在 $[a, b] \subset \mathbb{R}$ 上的一般线性二阶微分算子，我们写作： $$ Lu(x) = \alpha(x)\frac{d^2}{dx^2}u(x) + \beta(x)\frac{d}{dx}u(x) + \gamma(x)u(x) = f(x)~ $$ 假设 $u_1$ 和 $u_2$ 构成齐次问题 $Lu = 0$ 的一组线性无关解。给定格林函数满足齐次边界条件：$G(a, s) = G(b, s) = 0$ 我们可以通过要求：$u_1(a) = 0,\quad u_2(b) = 0$ 来构造 $G(x, s)$。满足这些条件的格林函数（同时满足函数连续性与导数 “跳跃” 条件）可以表示为： $$ G(x, s) = \begin{cases} \displaystyle \frac{u_1(x) u_2(s)}{\alpha(s)\mathcal{W}(s)}, & a \leq x < s \\ \displaystyle \frac{u_2(x) u_1(s)}{\alpha(s)\mathcal{W}(s)}, & s < x \leq b \end{cases}~ $$ 其中：$\mathcal{W}(x) = u_1(x) u_2'(x) - u_1'(x) u_2(x)$ 称为 $u_1$ 与 $u_2$ 的 Wronskian 行列式（或 Wronskian 判别式）。虽然这是一个相对受限的情形，但 Wronskian 在其他类型的边值问题中也频繁出现，尤其是在需要构造单边（先进或延迟）格林函数的问题中，包括那些带有边界导数条件（Neumann 条件）或在单一边界上同时对函数及其法向导数施加条件的问题（Cauchy 条件）。

合成格林函数

　　 如果微分算子 $L$ 可以因式分解为：$L = L_1 L_2$ 那么 $L$ 的格林函数 $G(x, s)$ 可以通过 $L_1$ 和 $L_2$ 的格林函数 $G_1$ 和 $G_2$ 构造如下： $$ G(x, s) = \int G_2(x, s_1) \, G_1(s_1, s) \, ds_1~ $$ 这个恒等式直接来自于将 $G(x, s)$ 视为算子 $L$ 的右逆的表示，类似于如下线性代数的情况：若有可逆线性算子 $C = (AB)^{-1} = B^{-1} A^{-1}$，那么其矩阵元可表示为 $C_{i,j}$。换句话说，组合两个算子的格林函数等价于先用 $G_1$ 处理源项，再将结果通过 $G_2$ 推送至目标点，从而构成完整算子的响应。

　　 当微分算子是导数的标量多项式时，即：$L = P_N(\partial_x)$ 我们可以利用代数学基本定理以及导数算子 $\partial_x$ 之间可交换的事实，将其分解为： $$ L = \prod_{i=1}^{N} (\partial_x - z_i)~ $$ 其中 $z_i$ 是多项式 $P_N(z)$ 的零点。对格林函数的定义式：$L G(x, s) = \delta(x - s)$ 同时对变量 $x$ 和 $s$ 进行傅里叶变换，得到： $$ \widehat{G}(k_x, k_s) = \frac{\delta(k_x - k_s)}{\prod_{i=1}^{N} (ik_x - z_i)}~ $$ 我们可以对上述分式进行部分分式分解，然后再进行傅里叶反变换，从而得到一系列将格林函数表示为多个格林函数积分的恒等式。例如，若：$L = (\partial_x + \gamma)(\partial_x + \alpha)^2$ 那么它的一种格林函数形式为： $$ \begin{aligned} G(x, s) =\;& \frac{1}{(\gamma - \alpha)^2} \, \Theta(x - s) e^{-\gamma(x - s)} \\ & - \frac{1}{(\gamma - \alpha)^2} \, \Theta(x - s) e^{-\alpha(x - s)} \\ & + \frac{1}{\gamma - \alpha} \, \Theta(x - s) (x - s) e^{-\alpha(x - s)} \\ =\;& \int \Theta(x - s_1)(x - s_1) e^{-\alpha(x - s_1)} \, \Theta(s_1 - s) e^{-\gamma(s_1 - s)} \, ds_1 \end{aligned}~ $$ 其中 $\Theta(x - s)$ 是阶跃函数。尽管这个例子在解析上是可解的，它也展示了一种更普适的构造方法：当算子较为复杂（例如为 $\nabla^2$ 拉普拉斯算子）时，该过程依然适用。这种技巧可以用于推导复杂微分算子的格林函数表达式。

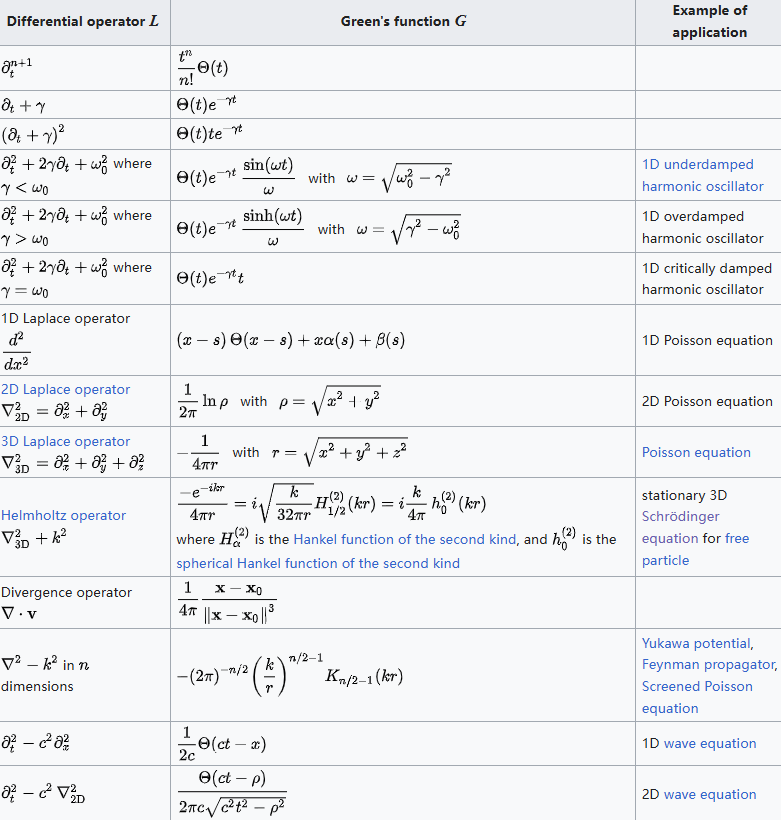
格林函数表

　　 下表概述了常见微分算子的格林函数，其中：$r = \sqrt{x^2 + y^2 + z^2}$，$\rho = \sqrt{x^2 + y^2}$，$\Theta(t)$ 表示海维赛德阶跃函数，$J_{\nu}(z)$ 表示贝塞尔函数，$I_{\nu}(z)$ 表示第一类修正贝塞尔函数，$K_{\nu}(z)$ 表示第二类修正贝塞尔函数。\(^\text{[9]}\) 当第一列中出现时间变量 $t$ 时，列出的是迟致（因果）格林函数。

图
图 2
图
图 3

5. 拉普拉斯算子的格林函数

　　 涉及拉普拉斯算子的线性微分算子的格林函数可以通过第二个格林恒等式直接应用。

　　 为了推导格林定理，先从散度定理（又称高斯定理）出发： $$ \int_V \nabla \cdot \mathbf{A} \, dV = \int_S \mathbf{A} \cdot d\hat{\boldsymbol{\sigma}}\,.~ $$ 令 $\mathbf{A} = \varphi \, \nabla \psi - \psi \, \nabla \varphi$ 并将其代入高斯定理中。

　　 计算 $\nabla \cdot \mathbf{A}$ 并对 ∇ 运算符应用乘积法则： $$ \begin{aligned} \nabla \cdot \mathbf{A} &= \nabla \cdot \left( \varphi \nabla \psi - \psi \nabla \varphi \right) \\ &= (\nabla \varphi) \cdot (\nabla \psi) + \varphi \nabla^2 \psi - (\nabla \varphi) \cdot (\nabla \psi) - \psi \nabla^2 \varphi \\ &= \varphi \nabla^2 \psi - \psi \nabla^2 \varphi. \end{aligned}~ $$ 将上述结果代入散度定理，就得到了格林定理： $$ \int_V \left( \varphi \nabla^2 \psi - \psi \nabla^2 \varphi \right) dV = \int_S \left( \varphi \nabla \psi - \psi \nabla \varphi \right) \cdot d\hat{\boldsymbol{\sigma}}.~ $$ 假设线性微分算子 $L$ 是拉普拉斯算子 $\nabla^2$，并存在相应的格林函数 $G$，则格林函数的定义性质仍然成立： $$ L G(\mathbf{x}, \mathbf{x}') = \nabla^2 G(\mathbf{x}, \mathbf{x}') = \delta(\mathbf{x} - \mathbf{x}').~ $$ 令 $\psi = G$，代入第二个格林恒等式（详见格林恒等式），得到： $$ \int_V \left[ \varphi(\mathbf{x}') \delta(\mathbf{x} - \mathbf{x}') - G(\mathbf{x}, \mathbf{x}') \nabla'^2 \varphi(\mathbf{x}') \right] d^3\mathbf{x}' = \int_S \left[ \varphi(\mathbf{x}') \nabla' G(\mathbf{x}, \mathbf{x}') - G(\mathbf{x}, \mathbf{x}') \nabla' \varphi(\mathbf{x}') \right] \cdot d\hat{\boldsymbol{\sigma}}'.~ $$ 这就是在拉普拉斯算子背景下应用格林函数的核心表达式。

　　 利用这个表达式，我们可以求解拉普拉斯方程 $\nabla^2 \varphi(\mathbf{x}) = 0$ 或泊松方程 $\nabla^2 \varphi(\mathbf{x}) = -\rho(\mathbf{x})$ 前提是满足诺伊曼边界条件或狄里克雷边界条件。换句话说，只要在某个体积的边界面上给定 (1) 函数 $\varphi(\mathbf{x})$ 的取值（狄里克雷边界条件），或 (2) 函数的法向导数（诺伊曼边界条件），那么我们就可以在整个体积内部求解出 $\varphi(\mathbf{x})$。

　　 假设我们的问题是要求解该区域内部的 $\varphi(\mathbf{x})$，那么积分 $$ \int_V \varphi(\mathbf{x}')\,\delta(\mathbf{x} - \mathbf{x}')\,d^3\mathbf{x}'~ $$ 由于狄拉克 δ 函数的定义性质，直接化简为 $\varphi(\mathbf{x})$，于是我们得到：

　　 $$ \varphi(\mathbf{x}) = -\int_V G(\mathbf{x}, \mathbf{x}')\,\rho(\mathbf{x}')\,d^3\mathbf{x}' + \int_S \left[ \varphi(\mathbf{x}')\,\nabla' G(\mathbf{x}, \mathbf{x}') - G(\mathbf{x}, \mathbf{x}')\,\nabla' \varphi(\mathbf{x}') \right] \cdot d\hat{\boldsymbol{\sigma}}'.~ $$

　　 这个形式表达了调和函数的一个著名性质：只要知道一个函数在边界面上的取值或法向导数，就可以确定它在体积内部的所有取值。

　　 在静电学中，$\varphi(\mathbf{x})$ 被解释为电势，$\rho(\mathbf{x})$ 为电荷密度，而 $\nabla \varphi(\mathbf{x}') \cdot d\hat{\boldsymbol{\sigma}}'$ 表示电场的法向分量。

　　 如果我们要解的是一个狄里克雷边值问题，那么格林函数应选择为当 $\mathbf{x}$ 或 $\mathbf{x}'$ 位于边界面上时满足 $G(\mathbf{x}, \mathbf{x}') = 0$。这样，表面积分中的两项就只剩下一项。

　　 如果问题是求解诺伊曼边值问题，看起来似乎应该选择使其法向导数在边界面上为零的格林函数。但实际上，如果我们将高斯定理应用于定义格林函数的微分方程，会得到： $$ \int_S \nabla' G(\mathbf{x}, \mathbf{x}') \cdot d\hat{\boldsymbol{\sigma}}' = \int_V \nabla'^2 G(\mathbf{x}, \mathbf{x}')\,d^3\mathbf{x}' = \int_V \delta(\mathbf{x} - \mathbf{x}')\,d^3\mathbf{x}' = 1,~ $$ 这意味着格林函数的法向导数在边界面上不可能为零，因为它必须在整个边界上积分为 1\(^\text{[10]}\)。

　　 法向导数最简单的形式是常数，即 $1/S$，其中 $S$ 是边界面的面积。此时解中的表面积分项变为： $$ \int_S \varphi(\mathbf{x}')\,\nabla' G(\mathbf{x}, \mathbf{x}') \cdot d\hat{\boldsymbol{\sigma}}' = \langle \varphi \rangle_S,~ $$ 其中 $\langle \varphi \rangle_S$ 表示势函数在边界面上的平均值。这个数值在一般情况下是未知的，但通常也不重要，因为我们更关注的是由势的梯度得到的电场，而不是势本身。

　　 在没有边界条件的情况下，拉普拉斯算子的格林函数（三维拉普拉斯方程的格林函数）为： $$ G(\mathbf{x}, \mathbf{x}') = -\frac{1}{4\pi |\mathbf{x} - \mathbf{x}'|}~ $$ 假设边界面延伸至无穷远处，并将该格林函数表达式代入求解电势函数的公式，最终得到电势与电荷密度之间的标准关系式： $$ \varphi(\mathbf{x}) = \int_V \frac{\rho(\mathbf{x}')}{4\pi \varepsilon |\mathbf{x} - \mathbf{x}'|} \, d^3\mathbf{x}'~ $$ 进一步阅读：泊松方程。

6. 示例

　　 求解以下问题的格林函数，其格林函数编号为 X11： $$ \begin{aligned} Lu &= u'' + k^2 u = f(x) \\ u(0) &= 0, \quad u\left(\frac{\pi}{2k}\right) = 0. \end{aligned}~ $$ 第一步：给定线性算子的格林函数定义为以下方程的解： $$ G''(x,s) + k^2 G(x,s) = \delta(x-s). \tag{Eq.*}~ $$ 当 $x \neq s$ 时，$\delta(x-s) = 0$，此时方程的通解为： $$ G(x,s) = c_1 \cos kx + c_2 \sin kx.~ $$ 当 $x < s$ 时，边界条件 $x = 0$ 给出： $$ G(0,s) = c_1 \cdot 1 + c_2 \cdot 0 = 0, \quad c_1 = 0,~ $$ 即 $$ G(x,s) = c_2 \sin kx, \quad x < s.~ $$ 当 $x > s$ 时，边界条件 $x = \frac{\pi}{2k}$

　　 给出： $$ G\left(\frac{\pi}{2k},s\right) = c_3 \cdot 0 + c_4 \cdot 1 = 0, \quad c_4 = 0,~ $$ 即 $$ G(x,s) = c_3 \cos kx, \quad x > s.~ $$ 总结目前的结果： $$ G(x,s) = \begin{cases} c_2 \sin kx, & x < s, \\ [0.4ex] c_3 \cos kx, & s < x. \end{cases}~ $$ 第二步：接下来需要确定 $c_{2}$ 和 $c_{3}$。

　　 要求格林函数在 $x = s$ 处连续，可得： $$ c_{2} \sin ks = c_{3} \cos ks~ $$ 为了保证一阶导数的不连续性，需将定义的微分方程（即式 \*）从 $x = s - \varepsilon$ 积分到 $x = s + \varepsilon$，并在 $\varepsilon \to 0$ 时取极限。注意，只需积分二阶导数项，因为其他项按构造是连续的： $$ c_{3} \cdot (-k \sin ks) - c_{2} \cdot (k \cos ks) = 1~ $$ 联立上述两个（不）连续性方程，解得： $$ c_{2} = -\frac{\cos ks}{k}, \quad c_{3} = -\frac{\sin ks}{k}~ $$ 因此，本问题的格林函数为： $$ G(x,s) = \begin{cases} -\dfrac{\cos ks}{k} \sin kx, & x < s, \\ -\dfrac{\sin ks}{k} \cos kx, & s < x. \end{cases}~ $$

7. 更多示例

8. 另见

9. 脚注

　　
a.技术术语中，“正规 (regular)” 意味着齐次问题 $f(x) = 0$ 只有平凡解 $u(x) = 0$ 存在。

10. 参考文献

  1. Wright, M. C. M. (2006-10-01). “格林函数还是格林的函数？” 《自然·物理学》，2 (10): 646. Bibcode:2006NatPh...2..646W. doi:10.1038/nphys411. ISSN 1745-2473.
  2. Khorrami, Mohammad (2021). “不同维度下波动方程的格林函数”。《米什科尔茨数学通报》，22 (2): 721. doi:10.18514/mmn.2021.2922. ISSN 1787-2405.
  3. Yu, Xiao; Lan, Kunquan; Wu, Jianhong (2021). “格林函数、线性二阶微分方程及一维扩散-对流模型”。《应用数学研究》，147 (1): 319–362. doi:10.1111/sapm.12384. ISSN 1467-9590.
  4. Chu, Yi-Zen; Starkman, Glenn D. (2011-11-10). “用于宇宙学和引力物理的扰动时空中的迟延格林函数”。《物理评论 D》，84 (12): 124020. arXiv:1108.1825. Bibcode:2011PhRvD..84l4020C. doi:10.1103/PhysRevD.84.124020.
  5. Soares de Castro, Antonio (2024-09-01). “一阶微分方程的迟延和超前格林函数”。《物理学报·手稿》，99 (9): 096101. Bibcode:2024PhyS...99i6101S. doi:10.1088/1402-4896/ad6bc7. ISSN 0031-8949.
  6. Camargo, Rubens de Figueiredo; Chiacchio, Ary Orozimbo; de Oliveira, Edmundo Capelas (2013-03-06). “单边与双边格林函数”。《边值问题》，2013 (1): 45. doi:10.1186/1687-2770-2013-45. hdl:11449/113526. ISSN 1687-2770.
  7. Jackson, John David (2009). 《经典电动力学》（第 3 版，[再版]）。霍博肯，纽约：Wiley 出版社。ISBN 978-0-471-30932-1.
  8. Cole, K.D.; Beck, J.V.; Haji-Sheikh, A.; Litkouhi, B. (2011). “获取格林函数的方法”。见 《利用格林函数的热传导》。Taylor and Francis 出版社。pp. 101–148. ISBN 978-1-4398-1354-6.
  9. 部分示例取自：Schulz, Hermann (2001). 《用铅笔学物理：自然科学家的分析工具》（第 4 版）。美因河畔法兰克福：Deutsch 出版社。ISBN 978-3-8171-1661-4.
  10. Jackson, John David (1998-08-14). 《经典电动力学》。John Wiley & Sons 出版社。p. 39.

引用文献

11. 外部链接

                     

© 保留一切权利