Floyd 判圈算法

                     

贡献者： int256

1. Floyd 判圈算法

　　 首先需要注意的一点，Floyd 判圈算法不是 Floyd 全源最短路算法。Floyd 判圈算法是用来判断链表中是否有圈（或环）的存在的。

　　 Floyd 判圈算法（又称为 Floyd 判环算法或龟兔赛跑算法）的思想类似于快慢指针。原理是 “龟兔赛跑”，慢指针每次向前移动 $1$ 步、快指针每次向前移动两步。如果两者在遍历链表的过程中相遇，则说明链表存在一个圈；如果快指针达到了链表的结尾（有尾则一定无环），说明链表无环。

　　 下面给出一个常见的实现方法：

bool hasCyc(ListNod* head) {
    if(head == nullptr)  return false;
    ListNod *slow = head, *fast = head;
    fast = fast -> next;

    while(fast != nullptr && fast -> next != nullptr) {
        if(slow == fast)  return true;
        slow = slow -> next;
        fast = fast -> next -> next;
    }
    
    return false;
}

2. Floyd 判圈算法的拓展

求环的长度

　　 在找到环后可以很容易地求出环的长度，固定 fast 快指针不动，然后让 slow 慢指针一直移动直到再与 fast 快指针相遇，这移动的距离恰好就是环的长度。

求环的起点

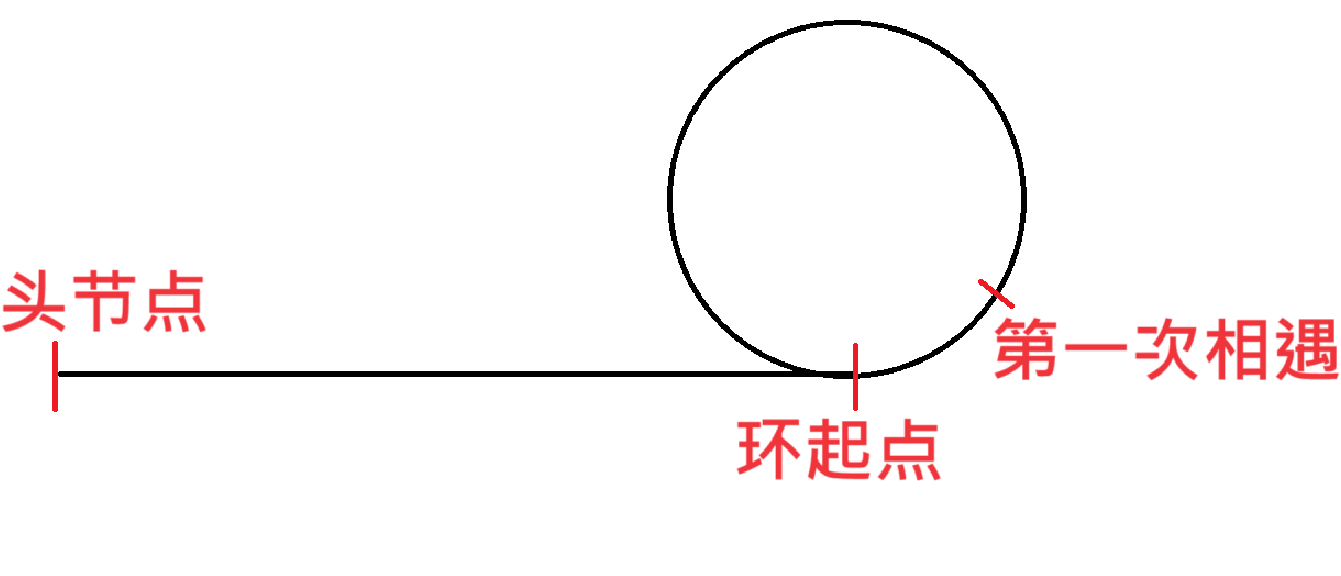
　　 假设链表是类似于如下形式：

　　 不失一般性地，考虑这个环的逆时针走的。

　　 设环长 $L$（可以通过刚才的方法求出），非环部分（也就是头节点到环）长 $a$，环的起点到快慢指针第一次相遇点的距离为 $b$（对应图的劣弧部分）、剩余的优弧长 $c = L-b$。设快指针走了 $f$ 圈、慢指针走了 $s$ 圈。

　　 而我们知道，快慢指针速度是两倍关系，而 $s_{fast} = a + b + fL$、$s_{slow} = a+ b + sL$，故 $s_{fast} = 2 s_{slow}$，故 $(f-2s)L = a+b$，即 $a+b$ 是 $L$ 的整数倍。不妨设 $a+b = k L$，即 $a+b=k (b+c)$，则 $a = (k-1)(b+c)+c$。所以我们可以让一个指针停留在首次相遇位置，另一个指针回到起点。这两个指针以相同速度同时再出发，必定会在环起点的位置相遇。

　　 注意这里，快慢指针要从同一起点出发。快指针 fast 不可以先走一步。

ListNod* getCycBeginNod(ListNod* head) {
    if(head == nullptr)  return nullptr;
    ListNod *slow = head, *fast = head;

    while(fast != nullptr && fast->next != nullptr) {
        slow = slow -> next, fast = fast -> next -> next;
        if(slow == fast) {
            // 发现环后, 一指针停留，另一指针回起点
            slow = head;
            while(slow != fast) {
                slow = slow -> next, fast = fast -> next;
            }
            return slow;
        }
    }
    return nullptr;
}