分部积分法（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在微积分中，更一般地说，在数学分析中，分部积分（integration by parts，或称偏积分 partial integration）是一种方法，用来将函数乘积的积分，转化为它们的导数与原函数乘积的积分形式。它常用于把一个函数乘积的不定积分转化为另一个更容易求解的不定积分。这个公式可以被看作是微分中乘积法则的积分版本；事实上，它正是由乘积法则推导而来的。

　　 分部积分公式表述如下： $$ \begin{aligned} \int_{a}^{b} u(x)\,v'(x)\,dx &= \Big[u(x)v(x)\Big]_{a}^{b} - \int_{a}^{b} u'(x)\,v(x)\,dx \\ &= u(b)v(b) - u(a)v(a) - \int_{a}^{b} u'(x)\,v(x)\,dx . \end{aligned}~ $$ 或者，设 $u = u(x), \quad du = u'(x)\,dx, \quad v = v(x), \quad dv = v'(x)\,dx$,则公式可以写得更为简洁： $$ \int u\,dv = uv - \int v\,du .~ $$ 前一个公式写作定积分形式，而后一个公式则写作不定积分形式。若对后者加上适当的积分限，应当能得到前者，但后者并不必然与前者等价。

　　 数学家布鲁克·泰勒于 1715 年首次发表了分部积分的思想。对于 Riemann–Stieltjes 积分与 Lebesgue–Stieltjes 积分，存在更一般化的分部积分形式。而在序列的离散情形中，其对应的类比被称为分部求和。

1. 定理

两个函数的乘积

　　 该定理可以如下推导。对于两个连续可微函数 $u(x)$ 和 $v(x)$，乘积法则表明： $$ (u(x)v(x))' = u'(x)v(x) + u(x)v'(x).~ $$ 对等式两边关于 $x$ 积分： $$ \int (u(x)v(x))'\,dx = \int u'(x)v(x)\,dx + \int u(x)v'(x)\,dx,~ $$ 注意到不定积分就是原函数，便得到： $$ u(x)v(x) = \int u'(x)v(x)\,dx + \int u(x)v'(x)\,dx,~ $$ 其中省略了积分常数。由此得到分部积分公式： $$ \int u(x)v'(x)\,dx = u(x)v(x) - \int u'(x)v(x)\,dx,~ $$ 或者用微分形式表示： $$ du = u'(x)\,dx, \quad dv = v'(x)\,dx,~ $$ 则有： $$ \int u(x)\,dv = u(x)v(x) - \int v(x)\,du.~ $$ 这应当理解为函数之间的相等式，两边均可加上一个未指定的常数。若在 $x=a$ 与 $x=b$ 两点取差，并应用微积分基本定理，就得到定积分形式： $$ \int_{a}^{b} u(x)v'(x)\,dx = u(b)v(b) - u(a)v(a) - \int_{a}^{b} u'(x)v(x)\,dx.~ $$ 原始积分 $\int u v'\,dx$ 包含导数 $v'$；要应用该定理，必须先找到 $v$，即 $v'$ 的一个原函数，然后再计算所得积分 $\int v u'\,dx$。

较低光滑性函数情况下的有效性

　　 并不要求 $u$ 和 $v$ 必须是连续可微的。当 $u$ 是绝对连续的，并且指定为 $v'$ 的函数是 Lebesgue 可积的（但不一定连续），分部积分公式依然成立。\(^\text{[3]}\)（如果 $v'$ 在某点不连续，那么它的原函数 $v$ 在该点可能没有导数。）

　　 若积分区间不是紧区间，则不需要 $u$ 在整个区间上绝对连续，也不需要 $v'$ 在整个区间上 Lebesgue 可积，如下的一些例子（其中 $u$ 与 $v$ 是连续且连续可微的）所示。例如： $$ u(x) = e^x/x^2, \quad v'(x) = e^{-x},~ $$ 此时 $u$ 在区间 $[1,\infty)$ 上并不是绝对连续的，但仍然有： $$ \int_{1}^{\infty} u(x)v'(x)\,dx = \Big[u(x)v(x)\Big]_{1}^{\infty} - \int_{1}^{\infty} u'(x)v(x)\,dx .~ $$ 只要 $[u(x)v(x)]_{1}^{\infty}$ 被理解为极限 $$ \lim_{L \to \infty} \big(u(L)v(L) - u(1)v(1)\big),~ $$ 并且只要右边的两个项都是有限的，那么公式仍然成立。这只在我们选择 $v(x) = -e^{-x}$ 时才为真。

　　 类似地，如果 $$ u(x) = e^{-x}, \quad v'(x) = x^{-1} \sin\left(x\right) ,~ $$ 则 $v'$ 在区间 $[1,\infty)$ 上并不是 Lebesgue 可积的，但依然有 $$ \int_{1}^{\infty} u(x)v'(x)\,dx = [u(x)v(x)]_{1}^{\infty} - \int_{1}^{\infty} u'(x)v(x)\,dx,~ $$ 并且应作同样的解释。

　　 同样，人们也可以很容易构造出类似的例子，其中 $u$ 和 $v$ 并不是连续可微的。

　　 进一步地，如果 $f(x)$ 是区间 $[a,b]$ 上的一个有界变差函数，而 $\varphi(x)$ 在 $[a,b]$ 上可微，则有 $$ \int_{a}^{b} f(x)\varphi'(x)\,dx = -\int_{-\infty}^{\infty} \widetilde{\varphi}(x)\, d\big(\widetilde{\chi}_{[a,b]}(x)\,\widetilde{f}(x)\big),~ $$ 其中 $$ d\big(\chi_{[a,b]}(x)\widetilde{f}(x)\big)~ $$ 表示对应于有界变差函数 $\chi_{[a,b]}(x)f(x)$ 的符号测度，而函数 $\widetilde{f}, \widetilde{\varphi}$ 是 $f, \varphi$ 在整个实数轴 $\mathbb{R}$ 上的扩展，分别为有界变差函数与可微函数。

多个函数的乘积

　　 对三个函数 $u(x), v(x), w(x)$ 的乘积法则进行积分，可以得到类似的结果： $$ \int_{a}^{b} uv\,dw \;=\; [uvw]_{a}^{b} - \int_{a}^{b} uw\,dv - \int_{a}^{b} vw\,du.~ $$ 一般而言，对于 $n$ 个因子的乘积，有： $$ \left(\prod_{i=1}^{n} u_i(x)\right)' \;=\; \sum_{j=1}^{n} u_j'(x)\,\prod_{i \neq j}^{n} u_i(x),~ $$ 由此可得： $$ \Bigg[\prod_{i=1}^{n} u_i(x)\Bigg]_{a}^{b} \;=\; \sum_{j=1}^{n} \int_{a}^{b} u_j'(x)\,\prod_{i \neq j}^{n} u_i(x).~ $$

2. 可视化

　　 考虑一个参数曲线 $(x,y) = (f(t), g(t))$.假设该曲线在局部是一一对应且可积的，我们可以定义： $$ x(y) = f(g^{-1}(y)), \quad y(x) = g(f^{-1}(x)).~ $$ 蓝色区域的面积为 $$ A_{1} = \int_{y_{1}}^{y_{2}} x(y)\,dy,~ $$ 同样，红色区域的面积为 $$ A_{2} = \int_{x_{1}}^{x_{2}} y(x)\,dx.~ $$ 总面积 $A_1 + A_2$ 等于大矩形的面积 $x_{2}y_{2}$，减去小矩形的面积 $x_{1}y_{1}$： $$ \overbrace{\int_{y_{1}}^{y_{2}} x(y)\,dy}^{A_{1}} + \overbrace{\int_{x_{1}}^{x_{2}} y(x)\,dx}^{A_{2}} = \Bigl. x \cdot y(x) \Bigr|_{x_{1}}^{x_{2}} = \Bigl. y \cdot x(y) \Bigr|_{y_{1}}^{y_{2}}.~ $$ 换用参数 $t$ 表示： $$ \int_{t_{1}}^{t_{2}} x(t)\,dy(t) + \int_{t_{1}}^{t_{2}} y(t)\,dx(t) = \Bigl. x(t)y(t) \Bigr|_{t_{1}}^{t_{2}}.~ $$ 换作不定积分形式，可以写作： $$ \int x\,dy + \int y\,dx = xy.~ $$ 整理得： $$ \int x\,dy = xy - \int y\,dx.~ $$ 因此，分部积分可以被理解为：通过矩形面积与红色区域面积，推导出蓝色区域的面积。

　　 这种可视化也解释了为什么当已知函数 $f(x)$ 的积分时，分部积分可以帮助求其反函数 $f^{-1}(x)$ 的积分。实际上，函数 $x(y)$ 与 $y(x)$ 互为反函数，而积分 $\int x\,dy$ 可以如上所示，通过已知的积分 $\int y\,dx$ 来计算。特别地，这说明了分部积分在处理对数函数与反三角函数积分时的应用。事实上，如果函数 $f$ 在某个区间上可微且一一对应，那么分部积分就可以用来推导一个公式，将 $f^{-1}$ 的积分表示为 $f$ 的积分。这一点在文章《反函数的积分》中已有展示。

3. 应用

寻找原函数

　　 分部积分是一种启发式方法，而不是纯粹的机械过程。给定一个函数需要积分时，常见的策略是巧妙地将该函数拆分为两个函数的乘积 $u(x)v(x)$，使得通过分部积分公式得到的剩余积分比原积分更容易计算。下面的形式有助于说明选择策略： $$ \int uv\,dx \;=\; u \int v\,dx \;-\; \int \Bigl(u' \int v\,dx\Bigr)\,dx .~ $$ 在右边，$u$ 被微分而 $v$ 被积分；因此，通常选择 $u$ 是一个在微分后简化的函数，或选择 $v$ 是一个在积分后简化的函数。一个简单的例子： $$ \int \frac{ \ln\left(x\right) }{x^{2}}\,dx .~ $$ 因为 $ \ln\left(x\right) $ 的导数是 $\tfrac{1}{x}$，所以令 $ \ln\left(x\right) $ 作为 $u$ 而 $\tfrac{1}{x^2}$ 的原函数是 $-\tfrac{1}{x}$，因此令 $\tfrac{1}{x^2}$ 作为 $v$。代入分部积分公式： $$ \int \frac{ \ln\left(x\right) }{x^{2}}\,dx = -\frac{ \ln\left(x\right) }{x} - \int \left(\frac{1}{x}\right)\left(-\frac{1}{x}\right)\,dx .~ $$ 其中 $-\tfrac{1}{x^2}$ 的原函数可以通过幂次法则求得，为 $\tfrac{1}{x}$，于是最终得到： $$ \int \frac{ \ln\left(x\right) }{x^{2}}\,dx = \left(-\frac{ \ln\left(x\right) + 1}{x}\right)\, + C~ $$ 其中 $C$ 是积分常数。

　　 或者，可以选择 $u$ 和 $v$，使得乘积 $u' \bigl(\int v\,dx\bigr)$ 因为消去而简化。例如，若要求解： $$ \int \sec^{2}(x)\cdot \ln\!\bigl(| \sin\left(x\right) |\bigr)\,dx.~ $$ 如果取 $u(x) = \ln\left(| \sin\left(x\right) |\right) $，$v(x) = \sec^{2}x$，那么由链式法则可得 $ u'(x) = \frac{1}{\tan x}$,而 $\sec^{2}x$ 的原函数是 $\tan x$。于是分部积分公式给出： $$ \int \sec^{2}(x)\cdot \ln\left(| \sin\left(x\right) |\right) \,dx = \tan\left(x\right) \cdot \ln\left(| \sin\left(x\right) |\right) - \int \tan\left(x\right) \cdot \frac{1}{ \tan\left(x\right) }\,dx .~ $$ 被积函数简化为 $1$，因此其原函数为 $x$。找到这种简化组合通常需要一定的尝试。

　　 在某些应用中，可能并不需要分部积分所产生的积分形式特别简单；例如在数值分析中，只要积分结果量级较小、对整体仅贡献微小的误差项就足够了。一些其他的特殊技巧将在下面的例子中展示。

　　 多项式与三角函数

　　 为了计算 $$ I = \int x \cos\left(x\right) \,dx,~ $$ 令： $$ \begin{aligned} u &= x \;\;\Rightarrow\;\; du = dx\\ dv &= \cos\left(x\right) \,dx \;\;\Rightarrow\;\; v = \int \cos\left(x\right) \,dx = \sin\left(x\right) \end{aligned}~ $$ 于是： $$ \begin{aligned} \int x \cos\left(x\right) \,dx &= \int u\,dv \\ &= u \cdot v - \int v\,du \\ &= x \sin\left(x\right) - \int \sin\left(x\right) \,dx \\ &= x \sin\left(x\right) + \cos\left(x\right) + C, \end{aligned}~ $$ 其中 $C$ 为积分常数。

　　 对于更高次幂的 $x$，如： $$ \int x^{n}e^{x}\,dx, \quad \int x^{n} \sin\left(x\right) \,dx, \quad \int x^{n} \cos\left(x\right) \,dx,~ $$ 可以反复应用分部积分来计算；每一次应用该定理都会使 $x$ 的幂次降低 1。

　　 指数函数与三角函数

　　 一个常用来展示分部积分运作方式的例子是： $$ I = \int e^{x} \cos\left(x\right) \,dx.~ $$ 在这里，需要进行两次分部积分。第一次令： $$ u = \cos\left(x\right) \;\;\Rightarrow\;\; du = - \sin\left(x\right) \,dx~ $$ $$ dv = e^{x}\,dx \;\;\Rightarrow\;\; v = \int e^{x}\,dx = e^{x}~ $$ 于是： $$ \int e^{x} \cos\left(x\right) \,dx = e^{x} \cos\left(x\right) + \int e^{x} \sin\left(x\right) \,dx.~ $$ 接着，为了计算剩下的积分，再次应用分部积分： $$ \begin{aligned} u &= \sin\left(x\right) \;\;\Rightarrow\;\; du = \cos\left(x\right) \,dx\\ dv &= e^{x}\,dx \;\;\Rightarrow\;\; v = \int e^{x}\,dx = e^{x}. \end{aligned}~ $$ 于是： $$ \int e^{x} \sin\left(x\right) \,dx = e^{x} \sin\left(x\right) - \int e^{x} \cos\left(x\right) \,dx.~ $$ 把结果代入前式： $$ \int e^{x} \cos\left(x\right) \,dx = e^{x} \cos\left(x\right) + e^{x} \sin\left(x\right) - \int e^{x} \cos\left(x\right) \,dx.~ $$ 此时，等式两边出现了相同的积分项。把它加到等式两边： $$ 2\int e^{x} \cos\left(x\right) \,dx = e^{x}\bigl[ \sin\left(x\right) + \cos\left(x\right) \bigr] + C,~ $$ 整理得： $$ \int e^{x} \cos\left(x\right) \,dx = \tfrac{1}{2}e^{x}\bigl[ \sin\left(x\right) + \cos\left(x\right) \bigr] + C',~ $$ 其中 $C$（以及 $C' = \tfrac{C}{2}$）为积分常数。

　　 类似的方法也可以用来计算 $\sec^{3}x$ 的积分。

　　 与常数 1 相乘的函数

　　 另外两个著名的例子是：当分部积分应用于一个函数与常数 $1$ 相乘的情形。这种方法在已知该函数的导数，并且已知其导数与 $x$ 相乘后的积分时有效。

　　 第一个例子是：$\int \ln\left(x\right) \,dx$.我们将其写作： $$ I = \int \ln\left(x\right) \cdot 1\,dx.~ $$ 令： $$ \begin{aligned} u &= \ln\left(x\right) \;\;\Rightarrow\;\; du = \frac{dx}{x},\\ dv &= dx \;\;\Rightarrow\;\; v = x. \end{aligned}~ $$ 于是： $$ \begin{aligned} \int \ln\left(x\right) \,dx &= x \ln\left(x\right) - \int \frac{x}{x}\,dx \\ &= x \ln\left(x\right) - \int 1\,dx \\ &= x \ln\left(x\right) - x + C, \end{aligned}~ $$ 其中 $C$ 是积分常数。

　　 第二个例子是反正切函数 $ \arctan\left(x\right) $： $$ I = \int \arctan\left(x\right) \,dx.~ $$ 将其改写为： $$ \int \arctan\left(x\right) \cdot 1\,dx.~ $$ 令： $$ \begin{aligned} u &= \arctan\left(x\right) \;\;\Rightarrow\;\; du = \frac{dx}{1+x^{2}},\\ dv &= dx \;\;\Rightarrow\;\; v = x. \end{aligned}~ $$ 于是： $$ \int \arctan\left(x\right) \,dx = x \arctan\left(x\right) - \int \frac{x}{1+x^{2}}\,dx.~ $$ 后一个积分利用反向链式法则和自然对数积分公式可得： $$ \int \arctan\left(x\right) \,dx = x \arctan\left(x\right) - \frac{ \ln\left(1+x^{2}\right) }{2} + C.~ $$

　　 LIATE 法则

　　 LIATE 法则是分部积分的一条经验规则。它的核心思想是：在以下列表中，优先选择排在前面的函数作为 $u$：[4]

　　 而作为 $dv$ 的函数则是列表中排在最后的函数。原因是：列表越靠后的函数通常具有比前面函数更简单的原函数。该规则有时也写作 “DETAIL”，其中 D 代表 $dv$，即取列表顶部的函数作为 $dv$。另一个变体是 ILATE 法则，它与 LIATE 的区别在于：反三角函数排在对数函数之前。

　　 为了演示 LIATE 法则，考虑积分： $$ \int x \cdot \cos\left(x\right) \,dx.~ $$ 按照 LIATE 法则，取 $u = x$，$dv = \cos\left(x\right) \,dx$，于是 $du = dx$，而 $$ v = \int \cos\left(x\right) \,dx = \sin\left(x\right) ,~ $$ 因此积分变为： $$ x \cdot \sin\left(x\right) - \int 1 \cdot \sin\left(x\right) \,dx,~ $$ 即： $$ x \cdot \sin\left(x\right) + \cos\left(x\right) + C.~ $$ 一般来说，我们会尽量选择 $u$ 和 $dv$，使得 $du$ 比 $u$ 更简单，同时 $dv$ 易于积分。如果反过来，取 $ \cos\left(x\right) $ 作为 $u$，而 $x\,dx$ 作为 $dv$，那么会得到： $$ \frac{x^{2}}{2} \cos\left(x\right) + \int \frac{x^{2}}{2} \sin\left(x\right) \,dx,~ $$ 这种形式在递归地应用分部积分公式后，显然会导致无限递归，从而得不到结果。

　　 尽管 LIATE 法则是一个有用的经验规则，但它也有例外。一个常见的替代方法是按照 “ILATE” 的顺序来考虑。此外，在某些情况下，多项式项需要以非平凡的方式拆分。

　　 例如，要计算： $$ \int x^{3}e^{x^{2}}\,dx,~ $$ 我们可以设： $$ u = x^{2}, \quad dv = x \cdot e^{x^{2}}\,dx,~ $$ 于是： $$ du = 2x\,dx, \quad v = \frac{e^{x^{2}}}{2}.~ $$ 因此： $$ \int x^{3}e^{x^{2}}\,dx = \int (x^{2})(x e^{x^{2}})\,dx = \int u\,dv = uv - \int v\,du = \frac{x^{2}e^{x^{2}}}{2} - \int xe^{x^{2}}\,dx.~ $$ 最后得到： $$ \int x^{3}e^{x^{2}}\,dx = \frac{e^{x^{2}}\,(x^{2}-1)}{2} + C.~ $$ 分部积分在数学分析中常常被用作证明定理的工具。

4. 华里士乘积

　　 圆周率 $\pi$ 的华里士无穷乘积公式为： $$ \begin{aligned} \frac{\pi}{2} &= \prod_{n=1}^{\infty} \frac{4n^{2}}{4n^{2}-1} = \prod_{n=1}^{\infty} \left(\frac{2n}{2n-1} \cdot \frac{2n}{2n+1}\right)\\ &= \left(\frac{2}{1}\cdot\frac{2}{3}\right)\cdot\left(\frac{4}{3}\cdot\frac{4}{5}\right)\cdot\left(\frac{6}{5}\cdot\frac{6}{7}\right)\cdot\left(\frac{8}{7}\cdot\frac{8}{9}\right)\cdot\;\cdots \end{aligned}~ $$ 该结果可以通过分部积分推导出来。

伽玛函数恒等式

　　 伽玛函数是一个特殊函数的例子，它在 $z > 0$ 时由广义积分定义。通过分部积分可以看出它是阶乘函数的推广： $$ \begin{aligned} \Gamma(z) &= \int_{0}^{\infty} e^{-x}x^{\,z-1}\,dx\\ &= -\int_{0}^{\infty} x^{\,z-1}\,d(e^{-x})\\ &= -\Bigl[e^{-x}x^{\,z-1}\Bigr]_{0}^{\infty} + \int_{0}^{\infty} e^{-x}\,d(x^{\,z-1})\\ &= 0 + \int_{0}^{\infty} (z-1)x^{\,z-2}e^{-x}\,dx\\ &= (z-1)\Gamma(z-1). \end{aligned}~ $$ 又因为 $$ \Gamma(1) = \int_{0}^{\infty} e^{-x}\,dx = 1,~ $$ 所以当 $z$ 为自然数，即 $z = n \in \mathbb{N}$ 时，反复应用该公式可得阶乘：$ \Gamma(n+1) = n!$.

在调和分析中的应用

　　 分部积分常用于调和分析，尤其是傅里叶分析，用来说明：当被积函数足够光滑时，快速振荡的积分会迅速衰减。最常见的例子是，用它来证明函数的傅里叶变换的衰减速度取决于该函数的光滑性，如下所述。

　　 导数的傅里叶变换

　　 如果函数 $f$ 是 $k$ 次连续可微的，并且其直到第 $k$ 阶的所有导数在无穷远处都趋于零，那么它的傅里叶变换满足： $$ (\mathcal{F}f^{(k)})(\xi) = (2\pi i \xi)^{k}\,\mathcal{F}f(\xi),~ $$ 其中 $f^{(k)}$ 表示 $f$ 的第 $k$ 阶导数。（右边常数的精确形式取决于所采用的傅里叶变换定义约定。）

　　 证明思路是利用： $$ \frac{d}{dy}e^{-2\pi i y \xi} = -2\pi i \xi \, e^{-2\pi i y \xi},~ $$ 因此，在对导数的傅里叶变换应用分部积分时，可以得到： $$ \begin{aligned} (\mathcal{F}f')(\xi) &= \int_{-\infty}^{\infty} e^{-2\pi i y \xi}\,f'(y)\,dy \\[6pt] &= \Bigl[e^{-2\pi i y \xi} f(y)\Bigr]_{-\infty}^{\infty} - \int_{-\infty}^{\infty} \bigl(-2\pi i \xi e^{-2\pi i y \xi}\bigr) f(y)\,dy \\[6pt] &= 2\pi i \xi \int_{-\infty}^{\infty} e^{-2\pi i y \xi} f(y)\,dy \\[6pt] &= 2\pi i \xi \,\mathcal{F}f(\xi). \end{aligned}~ $$ 通过归纳法推广，即可得到一般 $k$ 阶的结论。类似的方法也可以用来求函数导数的拉普拉斯变换。

　　 傅里叶变换的衰减性

　　 上述结果告诉我们傅里叶变换的衰减性质。因为若 $f$ 与 $f^{(k)}$ 都是可积的，那么有： $$ |{\mathcal{F}}f(\xi)| \;\leq\; \frac{I(f)}{1 + |2\pi \xi|^{k}}, \quad \text{其中 } I(f) = \int_{-\infty}^{\infty} \bigl(|f(y)| + |f^{(k)}(y)|\bigr)\,dy.~ $$ 换句话说，如果 $f$ 满足这些条件，那么它的傅里叶变换在无穷远处的衰减速度至少与 $1/|\xi|^{k}$ 一样快。特别地，当 $k \geq 2$ 时，傅里叶变换本身就是可积的。

　　 证明依赖于一个直接由傅里叶变换定义得到的不等式： $$ |{\mathcal{F}}f(\xi)| \;\leq\; \int_{-\infty}^{\infty} |f(y)|\,dy.~ $$ 将同样的思想应用于本节开头给出的等式，可得： $$ |(2\pi i \xi)^{k}{\mathcal{F}}f(\xi)| \;\leq\; \int_{-\infty}^{\infty} |f^{(k)}(y)|\,dy.~ $$ 将这两个不等式相加，再除以 $1 + |2\pi \xi|^{k}$，即可得到所述的不等式。

在算子理论中的应用

　　 分部积分在算子理论中的一个应用是：它能说明 $-\Delta$（其中 $\Delta$ 是拉普拉斯算子）在 $L^{2}$ 空间中是一个正算子（参见 $L^p$ 空间）。若 $f$ 是光滑且具有紧支集的函数，那么利用分部积分可得： $$ \begin{aligned} \langle -\Delta f, f \rangle_{L^{2}} &= -\int_{-\infty}^{\infty} f''(x)\,\overline{f(x)}\,dx\\ &= -\Bigl[f'(x)\,\overline{f(x)}\Bigr]_{-\infty}^{\infty} + \int_{-\infty}^{\infty} f'(x)\,\overline{f'(x)}\,dx\\ &= \int_{-\infty}^{\infty} |f'(x)|^{2}\,dx \;\geq\; 0. \end{aligned}~ $$

其他应用

5. 反复分部积分

　　 在分部积分公式左边的积分中考虑 $v$ 的二阶导数，提示我们可以在右边积分上反复应用分部积分： $$ \int u v''\,dx = uv' - \int u'v'\,dx = uv' - \bigl(u'v - \int u''v\,dx\bigr).~ $$ 将这种反复分部积分的概念扩展到 $n$ 阶导数时，可以得到： $$ \int u^{(0)}v^{(n)}\,dx = u^{(0)}v^{(n-1)} - u^{(1)}v^{(n-2)} + u^{(2)}v^{(n-3)} - \cdots + (-1)^{n-1}u^{(n-1)}v^{(0)} + (-1)^{n}\int u^{(n)}v^{(0)}\,dx,~ $$ 或更紧凑地写为： $$ \int u^{(0)}v^{(n)}\,dx = \sum_{k=0}^{n-1} (-1)^{k} u^{(k)} v^{(n-1-k)} + (-1)^{n}\int u^{(n)}v^{(0)}\,dx.~ $$ 这一思想在以下情况下很有用：当 $v^{(n)}$ 的连续积分容易求得（例如指数函数或正弦、余弦函数，如在拉普拉斯变换或傅里叶变换中），并且当 $u$ 的第 $n$ 阶导数为零时（例如次数为 $(n-1)$ 的多项式函数）。后一种情况会终止分部积分的重复过程，因为右边的积分消失。

　　 在上述反复分部积分的过程中，积分 $$ \int u^{(0)}v^{(n)}\,dx, \quad \int u^{(\ell)}v^{(n-\ell)}\,dx, \quad \int u^{(m)}v^{(n-m)}\,dx \quad (1 \leq m, \ell \leq n)~ $$ 彼此之间建立了联系。这可以解释为在被积函数中任意地 “转移” 导数，在 $v$ 与 $u$ 之间切换。这一方法同样十分有用（参见 Rodrigues 公式）。

表格式分部积分

　　 上述公式的核心过程可以用一个表格来总结；这种方法称为 “表格式积分”[5]，并在电影《为人师表》（Stand and Deliver, 1988）中出现过。[6]

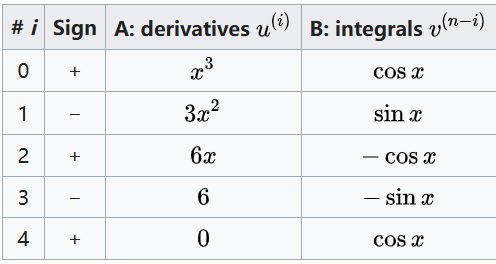
　　 例如，考虑积分： $$ \int x^{3}\cos x \, dx~ $$ 并取 $u^{(0)} = x^{3}, \quad v^{(n)} = \cos x$.

　　 在 $A$ 列中依次写下函数 $u^{(0)} = x^{3}$ 及其后续导数 $u^{(i)}$，直到结果为零为止。在 $B$ 列中依次写下函数 $v^{(n)} = \cos x$ 及其后续原函数 $v^{(n-i)}$，直到 $B$ 列的行数与 $A$ 列相同。

　　 结果如下所示：

图
图 1

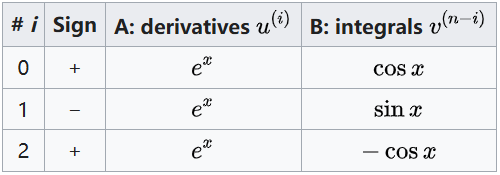
　　 $A$ 列与 $B$ 列中第 $i$ 行的项相乘，再配合相应的符号，就给出了在反复分部积分过程中第 $i$ 步对应的积分。当 $i = 0$ 时，得到原始积分。在 $i > 0$ 的步骤中，完整的结果必须将第 $i$ 个积分与之前所有的乘积相加：即 $A$ 列第 $j$ 项与 $B$ 列第 $(j+1)$ 项相乘（例如：$A$ 列第 1 项乘 $B$ 列第 2 项，$A$ 列第 2 项乘 $B$ 列第 3 项，依此类推），并加上第 $j$ 步对应的符号（$0 \leq j < i$）。当乘积为零时，过程自然结束（在该例中是 $i = 4$）。最终结果如下（每一项符号交替）： $$ \underbrace{(+1)(x^{3})(\sin x)}_{j=0} + \underbrace{(-1)(3x^{2})(-\cos x)}_{j=1} + \underbrace{(+1)(6x)(-\sin x)}_{j=2} + \underbrace{(-1)(6)(\cos x)}_{j=3} + \underbrace{\int (+1)(0)(\cos x)\,dx}_{i=4:\;\to C}.~ $$ 由此得到： $$ \underbrace{\int x^{3}\cos x\,dx}_{\text{step 0}} = x^{3}\sin x + 3x^{2}\cos x - 6x\sin x - 6\cos x + C.~ $$ 反复分部积分在以下情况下也很有用：当对函数 $u^{(i)}$ 与 $v^{(n-i)}$ 分别求导与积分时，它们的乘积会变成原始被积函数的某个倍数。在这种情形下，迭代可以在该索引 $i$ 处终止。这种情况往往出现在指数函数与三角函数中。例如，考虑积分： $$ \int e^{x}\cos x \, dx.~ $$

图
图 2

　　 在这种情况下，$A$ 列与 $B$ 列在 $i=2$ 时的乘积（配合相应符号）会得到原始被积函数的相反数（比较 $i=0$ 行与 $i=2$ 行）。 $$ \underbrace{\int e^{x}\cos x\,dx}_{\text{step 0}} = \underbrace{(+1)(e^{x})(\sin x)}_{j=0} + \underbrace{(-1)(e^{x})(-\cos x)}_{j=1} + \underbrace{\int(+1)(e^{x})(-\cos x)\,dx}_{i=2}.~ $$ 注意到右边的积分可以包含自己的积分常数 $C'$，把这个抽象的积分移到等式另一边，就得到： $$ 2\int e^{x}\cos x\,dx = e^{x}\sin x + e^{x}\cos x + C',~ $$ 最终： $$ \int e^{x}\cos x\,dx = \tfrac{1}{2}\bigl(e^{x}(\sin x + \cos x)\bigr) + C,~ $$ 其中 $C = \tfrac{C'}{2}$.

6. 高维情形

　　 分部积分可以扩展到多元函数的情形，其方法是将微积分基本定理的某种形式应用于合适的乘积法则。在多元微积分中存在若干种可能的配对方式，通常涉及一个标量函数 $u$ 和一个向量值函数（向量场 $V$。\(^\text{[7]}\)

　　 散度的乘积法则为： $$ \nabla \cdot (u\mathbf{V}) = u\,\nabla \cdot \mathbf{V} + \nabla u \cdot \mathbf{V}.~ $$ 设 $\Omega$ 是 $\mathbb{R}^n$ 中一个有界开子集，边界为分段光滑的 $\Gamma = \partial \Omega$。在 $\Omega$ 上用标准体积元 $d\Omega$ 积分，并应用散度定理，有： $$ \int_{\Gamma} u\mathbf{V} \cdot \hat{\mathbf{n}}\,d\Gamma = \int_{\Omega} \nabla \cdot (u\mathbf{V})\,d\Omega = \int_{\Omega} u\,\nabla \cdot \mathbf{V}\,d\Omega + \int_{\Omega} \nabla u \cdot \mathbf{V}\,d\Omega,~ $$ 其中 $\hat{\mathbf{n}}$ 是指向边界的单位外法向量，积分采用其标准黎曼体积元 $d\Gamma$。 整理得： $$ \int_{\Omega} u\,\nabla \cdot \mathbf{V}\,d\Omega = \int_{\Gamma} u\mathbf{V}\cdot \hat{\mathbf{n}}\,d\Gamma - \int_{\Omega} \nabla u \cdot \mathbf{V}\,d\Omega,~ $$ 换句话说： $$ \int_{\Omega} u\,\operatorname{div}(\mathbf{V})\,d\Omega = \int_{\Gamma} u\mathbf{V}\cdot \hat{\mathbf{n}}\,d\Gamma - \int_{\Omega} \operatorname{grad}(u)\cdot \mathbf{V}\,d\Omega.~ $$ 该定理的正则性要求可以放宽。例如，边界 $\Gamma = \partial \Omega$ 只需是 Lipschitz 连续的，而函数 $u, v$ 只需属于 Sobolev 空间 $H^{1}(\Omega)$。

格林第一恒等式

　　 设连续可微的向量场 $\mathbf{U} = u_{1}\mathbf{e}_{1} + \cdots + u_{n}\mathbf{e}_{n},\quad v\mathbf{e}_{1}, \ldots, v\mathbf{e}_{n}$，其中 $\mathbf{e}_{i}$ 是第 $i$ 个标准基向量，$i = 1, \ldots, n$。现在将上面的分部积分公式应用到每个 $u_{i}$ 与向量场 $v\mathbf{e}_{i}$ 的乘积上： $$ \int_{\Omega} u_{i}\,\frac{\partial v}{\partial x_{i}}\,d\Omega = \int_{\Gamma} u_{i}v\,\mathbf{e}_{i}\cdot \hat{\mathbf{n}}\,d\Gamma - \int_{\Omega} \frac{\partial u_{i}}{\partial x_{i}}\,v\,d\Omega.~ $$ 对所有 $i$ 求和后，得到新的分部积分公式： $$ \int_{\Omega} \mathbf{U}\cdot \nabla v\,d\Omega = \int_{\Gamma} v\,\mathbf{U}\cdot \hat{\mathbf{n}}\,d\Gamma - \int_{\Omega} v\,\nabla \cdot \mathbf{U}\,d\Omega.~ $$ 当 $\mathbf{U} = \nabla u$，且 $u \in C^{2}(\overline{\Omega})$ 时，该公式即为格林第一恒等式： $$ \int_{\Omega} \nabla u \cdot \nabla v\,d\Omega = \int_{\Gamma} v\,\nabla u \cdot \hat{\mathbf{n}}\,d\Gamma - \int_{\Omega} v\,\nabla^{2}u\,d\Omega.~ $$

微分形式

　　 外微分作用在微分形式上满足一个分级乘积法则。若 $u \in \Omega^{k}(M)$ 是一个 $k$-形式，$v \in \Omega^{n}(M)$ 是一个 $n$-形式，定义在一个可定向的 $(k+n+1)$-维有边界流形 $M$ 上，则有： $$ d(u \wedge v) = du \wedge v + (-1)^{k} u \wedge dv.~ $$ 在 $M$ 上对该等式两边积分： $$ \int_{M} d(u \wedge v) = \int_{M} du \wedge v + (-1)^{k} \int_{M} u \wedge dv.~ $$ 等价地： $$ \int_{M} du \wedge v = \int_{M} d(u \wedge v) - (-1)^{k} \int_{M} u \wedge dv.~ $$ 应用广义斯托克斯定理，可得其标准形式： $$ \int_{M} du \wedge v = \oint_{\partial M} u \wedge v - (-1)^{k} \int_{M} u \wedge dv.~ $$ 当 $u$ 与 $v$ 都取为 0-形式（即光滑函数）时，这一结果退化为经典情形。

7. 参见

8. 注释

  1. “Brook Taylor”. History.MCS.St-Andrews.ac.uk. 2018 年 5 月 25 日检索。
  2. “Brook Taylor”. Stetson.edu. 2018 年 1 月 3 日存档。2018 年 5 月 25 日检索。
  3. “Integration by parts”. Encyclopedia of Mathematics*.
  4. Kasube, Herbert E. (1983). “A Technique for Integration by Parts”. The American Mathematical Monthly. 90 (3): 210–211. doi:10.2307/2975556. JSTOR 2975556.
  5. Thomas, G. B.; Finney, R. L. (1988). Calculus and Analytic Geometry (第 7 版). Reading, MA: Addison-Wesley. ISBN 0-201-17069-8.
  6. Horowitz, David (1990). “Tabular Integration by Parts” (PDF). The College Mathematics Journal. 21 (4): 307–311. doi:10.2307/2686368. JSTOR 2686368.
  7. Rogers, Robert C. (2011 年 9 月 29 日). “The Calculus of Several Variables” (PDF).

9. 进一步阅读

10. 外部链接

                     

© 保留一切权利