分析力学(综述)
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章)
在理论物理和数学物理中,分析力学或理论力学是一系列紧密相关的经典力学表述。分析力学利用表示整个系统的标量运动性质——通常是其动能和势能。运动方程通过某种标量变化的基本原理从标量量推导出来。
分析力学是在牛顿力学之后,于 18 世纪及以后由许多科学家和数学家发展起来的。牛顿力学考虑运动的矢量量,特别是系统组成部分的加速度、动量、力等,因此也可以称为矢量力学。标量是一个数量,而矢量则由数量和方向表示。这两种方法的结果是等价的,但分析力学在处理复杂问题时具有许多优势。
分析力学利用系统的约束条件来解决问题。这些约束限制了系统的自由度,并可以用于减少求解运动所需的坐标数。这种形式适合任意选择的坐标,在此语境下称为广义坐标。系统的动能和势能用这些广义坐标或广义动量表示,运动方程可以轻松建立,因此,分析力学比完全矢量化的方法能够更高效地解决许多力学问题。然而,对于非保守力或如摩擦力等耗散力,分析力学并不总是有效,此时可以回归到牛顿力学。
分析力学的两个主要分支是拉格朗日力学(在构型空间中使用广义坐标及其对应的广义速度)和哈密顿力学(在相空间中使用坐标及对应的动量)。两种表述通过广义坐标、速度和动量上的勒让德变换互相等价,因此它们包含相同的信息来描述系统的动力学。还有其他表述方法,如哈密顿-雅可比理论、劳斯力学和阿佩尔运动方程。任意形式的粒子和场的运动方程都可以从广泛适用的最小作用量原理推导而出。其中一个结果是诺特定理,它将守恒定律与其相关对称性联系起来。
分析力学并没有引入新的物理概念,也不比牛顿力学更为普遍。它是一系列等效的形式,具有广泛的应用。事实上,相同的原理和形式可以用于相对论力学和广义相对论,并在经过一些修正后用于量子力学和量子场论。
分析力学广泛应用于基础物理学和应用数学,尤其是在混沌理论中。
分析力学的方法适用于离散粒子系统,每个粒子具有有限的自由度。它们可以被修改以描述具有无限自由度的连续场或流体。这些定义和方程与力学中的定义和方程有着密切的类比。
1. 分析力学的动机
力学理论的目标是解决物理学和工程学中出现的力学问题。从一个物理系统出发(如一个机械装置或一个恒星系统),建立一个微分方程形式的数学模型。该模型可以通过数值或解析方法求解,以确定系统的运动。
牛顿的矢量方法通过使用力、速度、加速度等矢量量来描述运动。这些量表征了被理想化为 “质点” 或 “粒子” 的物体的运动,即一个附有质量的单一质点。牛顿的方法已成功应用于广泛的物理问题中,包括粒子在地球引力场中的运动以及行星绕太阳的运动。在这种方法中,牛顿定律通过微分方程描述运动,问题随之简化为解该方程。
然而,当一个力学系统包含许多粒子时(如复杂的机械装置或流体),牛顿的方法难以应用。在适当的预防措施下(如将每个粒子与其他粒子隔离并确定作用在其上的所有力),可以使用牛顿的方法。然而,即使在相对简单的系统中,这样的分析也是繁琐的。牛顿认为他的第三定律 “作用等于反作用” 可以解决所有的复杂情况。【需要引用】但即使是旋转刚体等简单系统,这一说法也不完全正确。【需要澄清】在更复杂的系统中,矢量方法无法提供充分的描述。
分析方法通过将机械系统视为相互作用的粒子集合来简化问题,而不是将每个粒子视为孤立单元。在矢量方法中,必须分别确定每个粒子的力,而在分析方法中,只需知道一个单一的函数,它隐含地包含了系统中作用的所有力。这种简化通常通过先验规定的某些运动学条件来实现。然而,分析处理不需要知道这些力,而是将这些运动学条件视为已知。【需要引用】
然而,要推导出复杂机械系统的运动方程,仍需要一个统一的基础。【需要澄清】这种基础由各种变分原理提供:在每组方程背后,都有一个表达整个方程组含义的原理。给定一个被称为作用量的基本和普遍量,当某些其他力学量发生微小变化时,该作用量保持不变的原理生成所需的微分方程组。该原理的表述不依赖于任何特定的坐标系,所有结果都以广义坐标表示。这意味着分析运动方程在坐标变换下不会改变,这是矢量运动方程所不具备的不变性属性。【2】
对于 “解” 一组微分方程的确切含义并不完全清楚。当粒子的坐标以时间 \( t \) 和定义初始位置及速度的参数的简单函数表达时,问题被视为已解决。然而,“简单函数” 并不是一个明确的概念:如今,一个函数 \( f(t) \) 不再像牛顿时代那样仅被视为 \( t \) 的形式表达(基本函数),而通常被视为由 \( t \) 确定的量,无法清晰地界定 “简单” 与 “非简单” 函数的界限。如果仅谈论 “函数”,那么每个力学问题一旦在微分方程中被良好表述便已得到解决,因为给定初始条件,\( t \) 的值就能确定该时刻的坐标。特别是在现代计算机建模方法下,通过差分方程替代微分方程,可以以任何所需精度获得力学问题的数值解。
尽管缺乏精确定义,但显然,两体问题有一个简单的解,而三体问题则没有。两体问题可以通过涉及参数的公式来求解;通过改变这些参数的值,可以研究所有解的集合,也即问题的数学结构。此外,两体的运动可以形成准确的脑中图像或图示,且能和真实物体的运动与相互作用一样真实且精确。对于三体问题,尽管也可以为参数赋予特定值,但在这些指定值下的解或这些解的集合并不能揭示问题的数学结构。与许多其他问题一样,只有通过检验微分方程本身才能阐明其数学结构。
分析力学的目标更高远:它不仅旨在理解单个力学问题的数学结构,而且旨在理解一个广泛的问题类的结构,该问题类涵盖了大部分力学内容。分析力学专注于那些可以适用拉格朗日或哈密顿运动方程的系统,这类系统确实包含了非常广泛的力学问题。【3】
分析力学的发展的两个目标是:(i)通过开发适用于广泛领域的标准技术来增加可解问题的范围;(ii)理解力学的数学结构。然而,从长远来看,(ii)对(i)的帮助要大于仅专注于已经设计了特定方法的具体问题。
2. 内在运动
广义坐标与约束
在牛顿力学中,通常使用所有三个笛卡尔坐标或其他三维坐标系来描述物体在运动中的位置。然而,在物理系统中,一些结构或其他系统通常会限制物体的运动,使其不能朝某些方向或路径运动。因此,完整的笛卡尔坐标集通常是不必要的,因为这些约束决定了坐标之间不断变化的关系,这些关系可以通过与约束相对应的方程来建模。在拉格朗日和哈密顿形式中,约束被整合到运动的几何结构中,从而将坐标数减少到描述运动所需的最小数量。这些坐标称为广义坐标,记作 \( q_i \)(\( i = 1, 2, 3, \dots \))。【4】: 231
曲线坐标与广义坐标的区别
广义坐标包含了系统的约束条件。每个广义坐标 \( q_i \) 对应一个自由度(为了方便用索引 \( i = 1, 2, \dots, N \) 表示),即系统可以改变其构型的每一种方式,如曲线长度或旋转角度。广义坐标不同于曲线坐标。曲线坐标的数量等于位置空间的维数(通常为三维空间的 3),而广义坐标的数量不一定等于该维数;约束可以减少自由度的数量(因此也减少定义系统构型所需的广义坐标的数量),遵循以下通用规则:【5】【有疑问 – 讨论】 \[ [\text{位置空间的维数(通常为 3)}] \times [\text{系统的成分数量(“粒子”)}] - (\text{约束数量}) = (\text{自由度的数量}) = (\text{广义坐标的数量})~ \] 对于具有 \( N \) 个自由度的系统,可以将广义坐标收集为一个 \( N \)-元组: \[ \mathbf{q} = (q_1, q_2, \dots, q_N)~ \] 该元组的时间导数(用上标点表示)表示广义速度: \[ \frac{d\mathbf{q}}{dt} = \left(\frac{dq_1}{dt}, \frac{dq_2}{dt}, \dots, \frac{dq_N}{dt}\right) \equiv \dot{\mathbf{q}} = (\dot{q}_1, \dot{q}_2, \dots, \dot{q}_N).~ \]
达朗贝尔的虚功原理
主条目:达朗贝尔原理 达朗贝尔原理指出,在可逆位移下,由力所做的微小虚功为零,即力与系统的理想约束一致时所做的功为零。约束的概念很有用,因为它限制了系统的行为,并为求解系统的运动提供了步骤。达朗贝尔原理的方程为:【6】:265 \[ \delta W = \boldsymbol{\mathcal{Q}} \cdot \delta \mathbf{q} = 0 ~, \] 其中 \[ \boldsymbol{\mathcal{Q}} = (\mathcal{Q}_1, \mathcal{Q}_2, \dots, \mathcal{Q}_N)~ \] 是广义力(此处使用脚本体 \(\mathcal{Q}\) 而非普通体 \( Q \) 以避免与下文中的正则变换发生冲突),而 \( q \) 是广义坐标。这引出了牛顿运动定律在分析力学语言中的广义形式: \[ \boldsymbol{\mathcal{Q}} = \frac{d}{dt} \left( \frac{\partial T}{\partial \dot{\mathbf{q}}} \right) - \frac{\partial T}{\partial \mathbf{q}}, ~ \] 其中 \( T \) 为系统的总动能,符号 \[ \frac{\partial}{\partial \mathbf{q}} = \left( \frac{\partial}{\partial q_1}, \frac{\partial}{\partial q_2}, \dots, \frac{\partial}{\partial q_N} \right)~ \] 是一种有用的简写(关于此符号,参见矩阵微积分)。
约束
主条目:完整约束、刚性约束和流变约束 如果曲线坐标系由标准位置矢量 \( \mathbf{r} \) 定义,并且位置矢量可以表示为广义坐标 \( q \) 和时间 \( t \) 的函数形式: \[ \mathbf{r} = \mathbf{r} (\mathbf{q} (t), t)~ \] 并且此关系对所有时间 \( t \) 成立,那么 \( q \) 就称为完整约束。【7】当约束随时间变化时,矢量 \( \mathbf{r} \) 显式依赖于 \( t \),而不仅仅是因为 \( q(t) \)。对于时间无关的情况,约束也称为刚性约束;而对于时间相关的情况,则称为流变约束。【5】
3. 拉格朗日力学
引入广义坐标和基本拉格朗日函数: \[ L(\mathbf{q}, \mathbf{\dot{q}}, t) = T(\mathbf{q}, \mathbf{\dot{q}}, t) - V(\mathbf{q}, \mathbf{\dot{q}}, t)~ \] 其中 \( T \) 是整个系统的总动能,\( V \) 是总势能,接着通过变分法或使用上述公式导出欧拉-拉格朗日方程: \[ \frac{d}{dt} \left( \frac{\partial L}{\partial \mathbf{\dot{q}}} \right) = \frac{\partial L}{\partial \mathbf{q}} ~, \] 这是 \( N \) 个二阶常微分方程,每个方程对应一个 \( q_i(t) \)。
这种表述将实际路径描述为使动能时间积分最小的路径,假设总能量固定且对通过时间不施加限制。
拉格朗日表述使用系统的构型空间,即所有可能的广义坐标的集合: \[ \mathcal{C} = \{ \mathbf{q} \in \mathbb{R}^N \} ~, \] 其中 \( \mathbb{R}^N \) 是 \( N \) 维实数空间(参见集合构造符号)。欧拉-拉格朗日方程的特解称为(构型)路径或轨迹,即满足初始条件的特定 \( q(t) \)。通解形成一组可能的构型随时间变化的函数: \[ \{ \mathbf{q}(t) \in \mathbb{R}^N : t \geq 0, t \in \mathbb{R} \} \subseteq \mathcal{C} ~, \] 构型空间可以更普遍、甚至更深刻地通过拓扑流形和切丛来定义。
4. 哈密顿力学
通过拉格朗日量的勒让德变换,将广义坐标和速度 \((q, \dot{q})\) 替换为 \((q, p)\),即广义坐标和与之共轭的广义动量: \[ \mathbf{p} = \frac{\partial L}{\partial \mathbf{\dot{q}}} = \left( \frac{\partial L}{\partial \dot{q}_1}, \frac{\partial L}{\partial \dot{q}_2}, \cdots, \frac{\partial L}{\partial \dot{q}_N} \right) = (p_1, p_2, \cdots, p_N) ~, \] 并引入哈密顿量(以广义坐标和动量为变量): \[ H(\mathbf{q}, \mathbf{p}, t) = \mathbf{p} \cdot \mathbf{\dot{q}} - L(\mathbf{q}, \mathbf{\dot{q}}, t)~ \] 其中 “\(\cdot\)” 表示点积,这也引出了哈密顿方程: \[ \dot{\mathbf{p}} = -\frac{\partial H}{\partial \mathbf{q}} \,, \quad \dot{\mathbf{q}} = +\frac{\partial H}{\partial \mathbf{p}} ~, \] 这些方程构成了一组 \(2N\) 个一阶常微分方程,每个方程对应一个 \( q_i(t) \) 和 \( p_i(t) \)。勒让德变换的另一个结果是拉格朗日量和哈密顿量的时间导数关系: \[ \frac{dH}{dt} = -\frac{\partial L}{\partial t} ,~ \] 这通常被认为是哈密顿运动方程的一部分,附加于其他方程之上。广义动量可以按照与牛顿第二定律相同的方式,用广义力表示: \[ \dot{\mathbf{p}} = \boldsymbol{\mathcal{Q}} ~. \] 类似于构型空间,所有动量的集合即为广义动量空间: \[ \mathcal{M} = \{ \mathbf{p} \in \mathbb{R}^N \} ~. \] (“动量空间” 也称为 “k-空间”,在量子力学和波理论中指的是所有波矢量的集合,由德布罗意关系给出。)
所有位置和动量的集合构成相空间: \[ \mathcal{P} = \mathcal{C} \times \mathcal{M} = \{ (\mathbf{q}, \mathbf{p}) \in \mathbb{R}^{2N} \} ~, \] 即构型空间和广义动量空间的笛卡尔积。
哈密顿方程的一个特解称为相路径,即满足初始条件的特定曲线 \((q(t), p(t))\)。所有相路径的集合即微分方程的通解,称为相图: \[ \{ (\mathbf{q}(t), \mathbf{p}(t)) \in \mathbb{R}^{2N} : t \geq 0, t \in \mathbb{R} \} \subseteq \mathcal{P} ~. \]
泊松括号
所有动力学变量都可以从位置 \( q \)、动量 \( p \) 和时间 \( t \) 推导出来,并表示为这些变量的函数:\( A = A(q, p, t) \)。如果 \( A(q, p, t) \) 和 \( B(q, p, t) \) 是两个标量值的动力学变量,则泊松括号由广义坐标和动量定义为: \[ \{A, B\} \equiv \{A, B\}_{\mathbf{q}, \mathbf{p}} = \frac{\partial A}{\partial \mathbf{q}} \cdot \frac{\partial B}{\partial \mathbf{p}} - \frac{\partial A}{\partial \mathbf{p}} \cdot \frac{\partial B}{\partial \mathbf{q}} \equiv \sum_k \frac{\partial A}{\partial q_k} \frac{\partial B}{\partial p_k} - \frac{\partial A}{\partial p_k} \frac{\partial B}{\partial q_k} ~, \] 计算 \( A \) 的全导数,并将哈密顿方程代入结果中,得出 \( A \) 的时间演化: \[ \frac{dA}{dt} = \{A, H\} + \frac{\partial A}{\partial t} ~. \] 此方程与量子力学中海森堡图像的运动方程密切相关,在海森堡图像中,经典动力学变量成为量子算符(用上标 “^” 表示),泊松括号通过狄拉克的正则量子化被算符的对易子取代: \[ \{A, B\} \rightarrow \frac{1}{i \hbar} [\hat{A}, \hat{B}] ~. \]
5. 拉格朗日量和哈密顿量的性质
以下是拉格朗日量和哈密顿量函数之间的共同性质。【5】【8】
- 每个自由度的所有广义坐标 \( q_i(t) \)、速度 \( \dot{q}_i(t) \) 和动量 \( p_i(t) \) 彼此独立。函数的显式时间依赖性意味着该函数除了 \( q(t) \) 和 \( p(t) \) 外还将时间 \( t \) 作为变量,而不仅仅是通过 \( q(t) \) 和 \( p(t) \) 表现出隐式的时间独立性。
- 拉格朗日量在加上任何 \( q \) 和 \( t \) 的函数的总时间导数下不变,即: \[ L' = L + \frac{d}{dt}F(\mathbf{q}, t) ~, \] 因此每个拉格朗日量 \( L \) 和 \( L' \) 描述完全相同的运动。换句话说,系统的拉格朗日量不是唯一的。
- 同样地,哈密顿量在加上任何 \( q \)、\( p \) 和 \( t \) 的函数的偏时间导数下保持不变,即: \[ K = H + \frac{\partial}{\partial t}G(\mathbf{q}, \mathbf{p}, t) ~, \] (在这种情况下 \( K \) 是常用的字母)。该性质用于正则变换(见下文)。
- 如果拉格朗日量与某些广义坐标无关,则与这些坐标共轭的广义动量是运动的常量,即守恒量,这可以直接从拉格朗日方程得出: \[ \frac{\partial L}{\partial q_j} = 0 \rightarrow \frac{dp_j}{dt} = \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_j} = 0~ \] 这样的坐标称为 “循环” 或 “可忽略” 坐标。可以证明,哈密顿量在完全相同的广义坐标下也是循环的。
- 如果拉格朗日量与时间无关,则哈密顿量也与时间无关(即两者在时间上都是常量)。
- 如果动能是广义速度的二次齐次函数,并且拉格朗日量显式地与时间无关,那么: \[ T((\lambda \dot{q}_i)^2, (\lambda \dot{q}_j \lambda \dot{q}_k), \mathbf{q}) = \lambda^2 T((\dot{q}_i)^2, \dot{q}_j \dot{q}_k, \mathbf{q}) \,, \quad L(\mathbf{q}, \mathbf{\dot{q}})~ \] 其中 \( \lambda \) 是常数,则哈密顿量为总守恒能量,等于系统的总动能和势能: \[ H = T + V = E ~. \] 这是薛定谔方程的基础,直接插入量子算符即可得到该方程。
6. 最小作用量原理
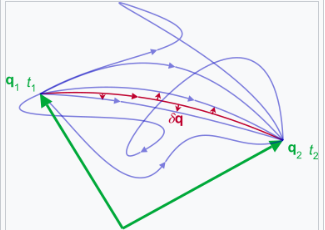
作用量是分析力学中的另一量,通过拉格朗日量定义为泛函: \[ \mathcal{S} = \int_{t_1}^{t_2} L(\mathbf{q}, \mathbf{\dot{q}}, t) \, dt ~. \] 从作用量找到运动方程的通用方法是最小作用量原理:【10】 \[ \delta \mathcal{S} = \delta \int_{t_1}^{t_2} L(\mathbf{q}, \mathbf{\dot{q}}, t) \, dt = 0 ~, \] 其中出发时间 \( t_1 \) 和到达时间 \( t_2 \) 是固定的。【1】术语 “路径” 或 “轨迹” 指的是系统作为构型空间 \( \mathcal{C} \) 中路径的时间演化,也就是说,\( q(t) \) 在 \( \mathcal{C} \) 中描绘出一条路径。作用量最小的路径即为系统实际经历的路径。
由此原理,可以推导出经典力学中的所有运动方程。该方法可以扩展到场而非粒子系统(见下文),并构成量子力学路径积分表述的基础【11】【12】,同时用于计算广义相对论中的测地线运动。【13】
7. 哈密顿-雅可比力学
哈密顿量的不变性(在加上任意 \( p \)、\( q \)、\( t \) 函数的偏时间导数下)允许将哈密顿量从一组坐标 \( q \) 和动量 \( p \) 转换为一组新的坐标 \( Q = Q(q, p, t) \) 和 \( P = P(q, p, t) \),可以通过四种可能的方式实现: \[ \begin{aligned} &K(\mathbf{Q}, \mathbf{P}, t) = H(\mathbf{q}, \mathbf{p}, t) + \frac{\partial}{\partial t} G_1(\mathbf{q}, \mathbf{Q}, t) \\ &K(\mathbf{Q}, \mathbf{P}, t) = H(\mathbf{q}, \mathbf{p}, t) + \frac{\partial}{\partial t} G_2(\mathbf{q}, \mathbf{P}, t) \\ &K(\mathbf{Q}, \mathbf{P}, t) = H(\mathbf{q}, \mathbf{p}, t) + \frac{\partial}{\partial t} G_3(\mathbf{p}, \mathbf{Q}, t) \\ &K(\mathbf{Q}, \mathbf{P}, t) = H(\mathbf{q}, \mathbf{p}, t) + \frac{\partial}{\partial t} G_4(\mathbf{p}, \mathbf{P}, t) \\ \end{aligned}~ \] 对 \( P \) 和 \( Q \) 的限制使得变换后的哈密顿系统为: \[ \mathbf{\dot{P}} = -\frac{\partial K}{\partial \mathbf{Q}} \,, \quad \mathbf{\dot{Q}} = +\frac{\partial K}{\partial \mathbf{P}} ~. \] 上述变换称为正则变换,每个函数 \( G_n \) 称为 “第 \( n \) 类” 或 “类型 \( n \)” 的生成函数。坐标和动量的变换可以简化哈密顿方程的求解。
\( Q \) 和 \( P \) 的选择是完全任意的,但并非所有选择都能构成正则变换。一个判断 \( q \to Q \) 和 \( p \to P \) 是否为正则变换的简单标准是泊松括号为 1: \[ \{ Q_i, P_i \} = 1~ \] 对于所有 \( i = 1, 2, \dots, N \)。如果不满足此条件,则该变换不是正则的。【5】
哈密顿-雅可比方程 将正则变换后的哈密顿量设为 \( K = 0 \),并将类型 2 的生成函数设为哈密顿主函数(也即作用量 \( \mathcal{S} \))加上一个任意常数 \( C \): \[ G_2(\mathbf{q}, t) = \mathcal{S}(\mathbf{q}, t) + C ~. \] 广义动量变为: \[ \mathbf{p} = \frac{\partial \mathcal{S}}{\partial \mathbf{q}}~ \] 并且 \( P \) 是常数,则哈密顿-雅可比方程(HJE)可以通过类型 2 的正则变换推导出: \[ H = -\frac{\partial \mathcal{S}}{\partial t}~ \] 其中 \( H \) 是哈密顿量,如之前所定义: \[ H = H(\mathbf{q}, \mathbf{p}, t) = H\left(\mathbf{q}, \frac{\partial \mathcal{S}}{\partial \mathbf{q}}, t\right)~ \] 另一个相关的函数是哈密顿特征函数: \[ W(\mathbf{q}) = \mathcal{S}(\mathbf{q}, t) + Et~ \] 用于通过对时间无关的哈密顿量 \( H \) 进行可加变量分离来求解 HJE。
对哈密顿-雅可比方程解的研究自然引向辛流形和辛拓扑的研究。【14】【15】在这种表述中,哈密顿-雅可比方程的解是哈密顿向量场的积分曲线。
8. 劳斯力学
劳斯力学是拉格朗日力学和哈密顿力学的混合表述,不常用但在消除循环坐标时尤其有用。【需要引用】如果一个系统的拉格朗日量有 \( s \) 个循环坐标 \( q = q_1, q_2, \dots, q_s \) 和共轭动量 \( p = p_1, p_2, \dots, p_s \),其余坐标为非循环坐标,记为 \( \zeta = \zeta_1, \zeta_2, \dots, \zeta_{N - s} \),则可以通过引入劳斯量来消除循环坐标: \[ R = \mathbf{p} \cdot \mathbf{\dot{q}} - L(\mathbf{q}, \mathbf{p}, \boldsymbol{\zeta}, \dot{\boldsymbol{\zeta}})~ \] 这引出了 \( s \) 个循环坐标 \( q \) 的 2 个哈密顿方程: \[ \dot{\mathbf{q}} = +\frac{\partial R}{\partial \mathbf{p}} \,, \quad \dot{\mathbf{p}} = -\frac{\partial R}{\partial \mathbf{q}} ~, \] 以及 \( N - s \) 个非循环坐标 \( \zeta \) 的拉格朗日方程: \[ \frac{d}{dt} \frac{\partial R}{\partial \dot{\boldsymbol{\zeta}}} = \frac{\partial R}{\partial \boldsymbol{\zeta}} ~. \] 以这种方式建立后,尽管劳斯量的形式类似于哈密顿量,但可以将其视为具有 \( N - s \) 个自由度的拉格朗日量。
坐标 \( q \) 不必是循环的,在哈密顿方程和拉格朗日方程中进入的坐标分区是任意的。让哈密顿方程消除循环坐标、拉格朗日方程处理非循环坐标只是出于方便。
9. 阿佩尔力学
阿佩尔运动方程涉及广义加速度,即广义坐标的二阶时间导数: \[ \alpha_r = \ddot{q}_r = \frac{d^2 q_r}{dt^2} ~, \] 以及前述达朗贝尔原理中的广义力。方程为: \[ \mathcal{Q}_r = \frac{\partial S}{\partial \alpha_r} \,, \quad S = \frac{1}{2} \sum_{k=1}^{N} m_k \mathbf{a}_k^2 ~, \] 其中 \[ \mathbf{a}_k = \ddot{\mathbf{r}}_k = \frac{d^2 \mathbf{r}_k}{dt^2}~ \] 是第 \( k \) 个粒子的加速度,即其位置矢量的二阶时间导数。每个加速度 \( \mathbf{a}_k \) 都用广义加速度 \( \alpha_r \) 表示,同样每个位置 \( \mathbf{r}_k \) 都用广义坐标 \( q_r \) 表示。
10. 经典场论
拉格朗日场论
广义坐标适用于离散粒子。对于 \( N \) 个标量场 \( \phi_i(r, t) \)(其中 \( i = 1, 2, \dots, N \)),拉格朗日密度是这些场及其空间和时间导数的函数,可能还包括空间和时间坐标本身: \[ \mathcal{L} = \mathcal{L}(\phi_1, \phi_2, \dots, \nabla \phi_1, \nabla \phi_2, \dots, \partial_t \phi_1, \partial_t \phi_2, \dots, \mathbf{r}, t) ~. \] 欧拉-拉格朗日方程在场的情况下有对应的形式: \[ \partial_\mu \left( \frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi_i)} \right) = \frac{\partial \mathcal{L}}{\partial \phi_i} ~, \] 其中 \( \partial_\mu \) 表示四维梯度,并使用了求和约定。对于 \( N \) 个标量场,这些拉格朗日场方程构成了场的 \( N \) 个二阶偏微分方程组,通常是耦合的非线性方程。
此标量场表述可扩展至矢量场、张量场和旋量场。
拉格朗日量为拉格朗日密度的体积分:【12】【16】 \[ L = \int_{\mathcal{V}} \mathcal{L} \, dV ~. \] 该表述最初为经典场发展,但适用于所有物理场,包括经典、量子和相对论情形,如牛顿引力、经典电磁学、广义相对论和量子场论。关键在于确定正确的拉格朗日密度以生成正确的场方程。
哈密顿场论
与 \( N \) 个标量场 \( \phi_i(r, t) \) 共轭的对应 “动量” 场密度为:【12】 \[ \pi_i(\mathbf{r}, t) = \frac{\partial \mathcal{L}}{\partial \dot{\phi}_i} \,, \quad \dot{\phi}_i \equiv \frac{\partial \phi_i}{\partial t}~ \] 在此上下文中,上标点表示偏时间导数,而非总时间导数。哈密顿密度 \( \mathcal{H} \) 类似于力学定义为: \[ \mathcal{H}(\phi_1, \phi_2, \dots, \pi_1, \pi_2, \dots, \mathbf{r}, t) = \sum_{i=1}^N \dot{\phi}_i(\mathbf{r}, t) \pi_i(\mathbf{r}, t) - \mathcal{L} ~. \] 运动方程为: \[ \dot{\phi}_i = +\frac{\delta \mathcal{H}}{\delta \pi_i} \,, \quad \dot{\pi}_i = -\frac{\delta \mathcal{H}}{\delta \phi_i} ~, \] 其中变分导数 \[ \frac{\delta}{\delta \phi_i} = \frac{\partial}{\partial \phi_i} - \partial_\mu \frac{\partial}{\partial (\partial_\mu \phi_i)}~ \] 必须替代单纯的偏导数。对于 \( N \) 个场,这些哈密顿场方程构成了一组 \( 2N \) 个一阶偏微分方程,通常是耦合且非线性的。
同样,哈密顿密度的体积分为哈密顿量: \[ H = \int_{\mathcal{V}} \mathcal{H} \, dV ~. \]
11. 对称性、守恒与诺特定理
经典空间和时间中的对称变换
每种变换都可以通过一个算符来描述(即作用于位置 \( \mathbf{r} \) 或动量 \( \mathbf{p} \) 变量的函数,以改变它们)。以下是算符不改变 \( \mathbf{r} \) 或 \( \mathbf{p} \) 的情况,即对称性。【11】
| 变换 | 算符 | 位置 | 动量 |
| 平移对称性 | \( X(\mathbf{a}) \) | \( \mathbf{r} \to \mathbf{r} + \mathbf{a} \) | \( \mathbf{p} \to \mathbf{p} \) |
| 时间平移 | \( U(t_0) \) | \( \mathbf{r}(t) \to \mathbf{r}(t + t_0) \) | \( \mathbf{p}(t) \to \mathbf{p}(t + t_0) \) |
| 旋转不变性 | \( R(\hat{\mathbf{n}}, \theta) \) | \( \mathbf{r} \to R(\hat{\mathbf{n}}, \theta) \mathbf{r} \) | \( \mathbf{p} \to R(\hat{\mathbf{n}}, \theta) \mathbf{p} \) |
| 伽利略变换 | \( G(\mathbf{v}) \) | \( \mathbf{r} \to \mathbf{r} + \mathbf{v}t \) | \( \mathbf{p} \to \mathbf{p} + m \mathbf{v} \) |
| 奇偶性(反演对称) | \( P \) | \( \mathbf{r} \to -\mathbf{r} \) | \( \mathbf{p} \to -\mathbf{p} \) |
| 时间反演对称性 | \( T \) | \( \mathbf{r} \to \mathbf{r}(-t) \) | \( \mathbf{p} \to -\mathbf{p}(-t) \) |
其中 \( R(\hat{\mathbf{n}}, \theta) \) 是绕由单位向量 \( \hat{\mathbf{n}} \) 定义的轴和角度 \( \theta \) 的旋转矩阵。
诺特定理
诺特定理指出,作用量的连续对称变换对应于一个守恒定律,即在由参数 \( s \) 参数化的变换下,作用量(以及拉格朗日量)不变: \[ L[q(s, t), \dot{q}(s, t)] = L[q(t), \dot{q}(t)]~ \] 拉格朗日量描述了与 \( s \) 无关的相同运动,其中 \( s \) 可以是长度、旋转角度或时间。与 \( q \) 对应的动量将守恒。【5】
12. 参见
- 拉格朗日力学
- 哈密顿力学
- 理论力学
- 经典力学
- 哈密顿-雅可比方程
- 哈密顿原理
- 运动学
- 动力学(物理学)
- 非自治力学
- Udwadia–Kalaba 方程【中立性存疑】
13. 参考文献和注释
- Lanczos, Cornelius (1970). *The Variational Principles of Mechanics* (4th ed.). New York: Dover Publications Inc. Introduction, pp. xxi–xxix. ISBN 0-486-65067-7.
- Lanczos, Cornelius (1970). *The Variational Principles of Mechanics* (4th ed.). New York: Dover Publications Inc. pp. 3–6. ISBN 978-0-486-65067-8.
- Synge, J. L. (1960). "Classical Dynamics". In Flügge, S. (ed.). *Principles of Classical Mechanics and Field Theory / Prinzipien der Klassischen Mechanik und Feldtheorie*. *Encyclopedia of Physics / Handbuch der Physik*. Vol. 2 / 3 / 1. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-642-45943-6. ISBN 978-3-540-02547-4. OCLC 165699220.
- Kibble, Tom, and Berkshire, Frank H. *Classical Mechanics* (5th Edition). Singapore: World Scientific Publishing Company, 2004.
- Analytical Mechanics*, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
- Torby, Bruce (1984). "Energy Methods". *Advanced Dynamics for Engineers*. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.
- McGraw Hill Encyclopaedia of Physics* (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3
- Classical Mechanics*, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- Penrose, R. (2007). *The Road to Reality*. Vintage Books. p. 474. ISBN 978-0-679-77631-4.
- Encyclopaedia of Physics* (2nd Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
- 量子力学,E. Abers,Pearson Ed.,Addison Wesley,Prentice Hall Inc,2004,ISBN 978-0-13-146100-0
- 量子场论,D. McMahon,McGraw Hill(美国),2008,ISBN 978-0-07-154382-8
- 相对论、引力与宇宙学,R.J.A. Lambourne,开放大学,剑桥大学出版社,2010,ISBN 978-0-521-13138-4
- Arnolʹd, V.I. (1989). 经典力学的数学方法 (第 2 版). Springer. 第 8 章. ISBN 978-0-387-96890-2.
- Doran, C.; Lasenby, A. (2003). 物理学家的几何代数. 剑桥大学出版社. §12.3,页 432–439. ISBN 978-0-521-71595-9.
- 引力,J.A. Wheeler,C. Misner,K.S. Thorne,W.H. Freeman & Co,1973,ISBN 0-7167-0344-0