单缝衍射的模拟(Matlab)
贡献者: addis
- 本文处于草稿阶段。
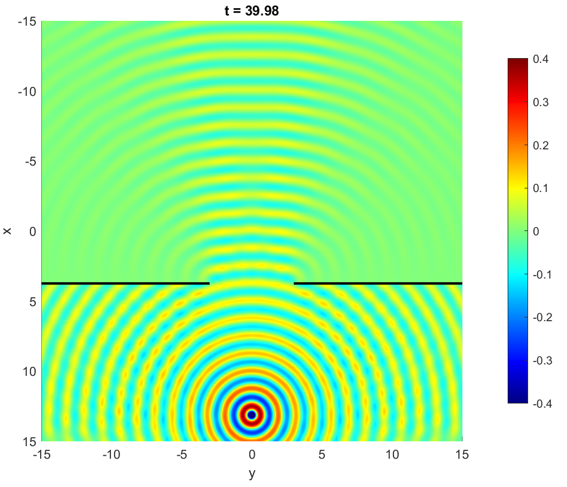
图 1:模拟结果,动画见这里。
挡板使用 Neumann 边界条件,其他边界使用开放边界条件。
代码 1:diffrac.m
% 二维波动方程的简单数值解
% 使用简单的差分法
function diffrac
% === 参数设置 ====
bc = 'o'; % 边界条件: [d] Dirichlet, [n] Neumann, [o] Open
v0 = 1;
Nplot = 20;
tmin = 0; tmax = 40; Nt = 2001;
xmin = -15; xmax = 15; Nx = 800;
ymin = -15; ymax = 15; Ny = 800;
crange = [-0.4,0.4];
ind_x0 = 750; ind_y0 = 400; % 波源
ind_x = 500; % 挡板
ind_y1 = 320; ind_y2 = 480;
% ================
close all;
t = linspace(tmin, tmax, Nt); dt = (tmax-tmin)/(Nt-1);
x = linspace(xmin, xmax, Nx); dx = (xmax-xmin)/(Nx-1);
y = linspace(ymin, ymax, Ny); dy = (ymax-ymin)/(Ny-1);
% [X, Y] = ndgrid(x, y);
Z = zeros(Nx, Ny, 3);
figure; set(gcf, 'Unit', 'Normalized', 'Position', [0.1,0.1,0.35,0.5]);
for it = 1:Nt
Z(ind_x0,ind_y0,2) = 2*sin(5*t(it));
d2Z = laplacian(Z(:,:,2), dx, dy);
if bc == 'd'
Z(:,:,3) = v0^2*dt^2*d2Z + 2*Z(:,:,2) - Z(:,:,1);
elseif bc == 'o'
Z(2:end-1,2:end-1,3) = (v0*dt)^2*d2Z(2:end-1, 2:end-1) +...
2*Z(2:end-1,2:end-1,2) - Z(2:end-1,2:end-1,1);
% ymax
grad_x = gradient(Z(:,end,2))/dx;
grad_y = (Z(:,end,2)-Z(:,end-1,2))/dy;
Z(:,end,3) = Z(:,end,2) ...
- (v0*dt)*sign(grad_y).*sqrt(grad_x.^2 + grad_y.^2);
% ymin
grad_x = gradient(Z(:,1,2))/dx;
grad_y = (Z(:,2,2)-Z(:,1,2))/dy;
Z(:,1,3) = Z(:,1,2) ...
+ (v0*dt)*sign(grad_y).*sqrt(grad_x.^2 + grad_y.^2);
% xmax
grad_x = (Z(end,:,2)-Z(end-1,:,2))/dx;
grad_y = gradient(Z(end,:,2))/dy;
Z(end,:,3) = Z(end,:,2) ...
- (v0*dt)*sign(grad_x).*sqrt(grad_x.^2 + grad_y.^2);
% xmin
grad_x = (Z(2,:,2)-Z(1,:,2))/dx;
grad_y = gradient(Z(1,:,2))/dy;
Z(1,:,3) = Z(1,:,2) ...
+ (v0*dt)*sign(grad_x).*sqrt(grad_x.^2 + grad_y.^2);
% left barrier
Z(ind_x,1:ind_y1,3) = Z(ind_x+1,1:ind_y1,2);
Z(ind_x-1,1:ind_y1,3) = Z(ind_x-2,1:ind_y1,2);
% right barrier
Z(ind_x,ind_y2:end,3) = Z(ind_x+1,ind_y2:end,2);
Z(ind_x-1,ind_y2:end,3) = Z(ind_x-2,ind_y2:end,2);
end
Z(:,:,1) = Z(:,:,2); Z(:,:,2) = Z(:,:,3);
% 画图
if mod(it, Nplot) == 0
clf; surfCart(x, y, Z(:,:,3)); caxis(crange);
colormap jet; shading interp; axis equal; hold on;
% plot barrier
plot3([1,1]*x(ind_x), [ymin, y(ind_y1)], [1,1]*0.4, ...
'Color', 'k', 'LineWidth', 2);
plot3([1,1]*x(ind_x), [y(ind_y2), ymax], [1,1]*0.4, ...
'Color', 'k', 'LineWidth', 2);
xlabel x; ylabel y; % view(78, 32);
axis([xmin,xmax,ymin,ymax,-2,2]);
set(gca, 'Unit', 'Normalized', 'Position', [0.1,0.2,0.7,0.68]);
title(['t = ' num2str(t(it), '%.2f')]);
saveas(gcf, [num2str(it/Nplot) '.png']);
end
end
end
% laplacian of Z(ix, iy)
% finite difference
% boundary condition (not included in Z) is 0
function d2Z = laplacian(Z, dx, dy)
N1 = size(Z, 1); N2 = size(Z, 2);
z1 = zeros(N1, 1); z2 = zeros(1, N2);
d2Z_1 = ([Z(2:end, :); z2] + [z2; Z(1:end-1, :)] - 2*Z)/dx^2;
d2Z_2 = ([Z(:, 2:end) z1] + [z1 Z(:, 1:end-1)] - 2*Z)/dy^2;
d2Z = d2Z_1 + d2Z_2;
end