中国科学院 2017 年考研普通物理
贡献者: Entanglement
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 选择题
- 单位质点在一个势能为 $V(r) = -\frac{a}{r}e^{-m_{o}r}+\frac{k}{2}r^{2}$ 的保守力场中运动,其中 $r$ 是质点离中心的径向距离,$(a,m_{0},k)$ 是势能参数。那么在该保守立场中,单位质点所受到的力为
A. $-\frac{ae^{-m_{0}r}}{r^{2}}-\frac{am_{0}e^{-m_{0}r}}{r}-kr$
B. $-\frac{ae^{-m_{0}r}}{r^{2}}-\frac{am_{0}e^{-m_{0}r}}{r}+kr$
C. $-kr$
D. $-\frac{ae^{-m_{0}r}}{r^{2}}-\frac{am_{0}e^{-m_{0}r}}{r}$
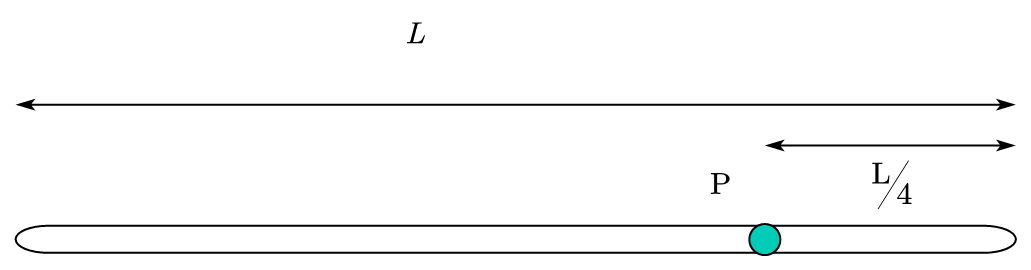
- 光滑水平桌面上静放一根长为 $L$ 的均质细杆,其质量为 $M$。已知 $P$ 点离杆的右端点距离为 $\frac{L}{4}$,如图所示。以 $P$ 点为轴心,转轴垂直于杆,则杆的转动惯量为
图 1:选择题 2 图示A. $\frac{1}{12}ML^{2} \quad$ B. $\frac{5}{24}ML^{2} \quad$ C. $\frac{7}{48}ML^{2} \quad$ D. $\frac{1}{24}ML^{2} \quad$ - 有一弹性介质,其介质密度记为 $\rho$.在该介质中,有一种机械振动,其振东量表示为 $\xi = \cos{[\omega(t-\frac{x}{u})]}$。下面有关介质中能量密度的说法正确的是
A. 能量密度只有动能项,其值为 $\frac{\rho}{2}\omega^{2}\sin^{2}{[\omega(t-\frac{x}{u})]}$
B. 能量密度只有势能项,其值为 $\frac{\rho}{2}\omega^{2}\cos^{2}{[\omega(t-\frac{x}{u})]}$
C. 能量密度包含动能项和势能项,其值为 $\rho\omega^{2}\sin^{2}{[\omega(t-\frac{x}{u})]}$
D. 能量密度包含动能项和势能项,其值为 $\rho\omega^{2}\cos^{2}{[\omega(t-\frac{x}{u})]}$
- 体积固定的容器内有一定量的气体,若温度升高,则分子的平均碰撞频率 $\underline{~~~~~~~~~~}$,分子的平均自由程 $\underline{~~~~~~~~~~}$。
A. 不变,减小 $\quad$ B. 不变,不变 $\quad$ C. 增大,减小 $\quad$ D. 增大,不变 $\quad$ - 如图所示,一个构成闭合电路的导电细线圈被扭成 “8” 字型(交叉处不接触),线圈的 1 部分比 2 部分面积大。将其放置在随时间变强的均匀磁场中,磁场方向与线圈所在的纸平面垂直并指向纸外,则线圈的 2 部分中电流是的方向为
A. 顺时针 $\quad$ B. 逆时针 $\quad$ C. 无电流 $\quad$ D. 不能确定 $\quad$图 2:选择题 5 图示 - 真空中,一半径为 $R$ 的球体均匀带电。在球内挖去一半径为 $r$ 的小球,且使球体其余部分带电分布不变。设小球空腔球心处为 $O$ 点。如果以无穷远处为电势零点,则在小球被挖去前后,关于 $O$ 点的电场强度和电势变化,下列说法正确的是
A. 电场强度和电势都不发生改变
B. 电场强度和电势都发生改变
C. 电场强度不发生改变,电势发生改变
D. 电场强度发生改变,电势不发生改变
- 钠原子处于基态时将束缚在最内层的一个电子移动到无穷远处的能量,与下面哪个能量量级最接近?
A. $1eV\quad$ B. $1keV\quad$ C. $1MeV\quad$ D. $1GeV\quad$ - 国际单位制,电阻的量纲是
A. $L^{2}MT^{-2}I^{-3}\quad$ B. $L^{2}MT^{-2}I^{-2}\quad$ C. $L^{2}MT^{-3}I^{-2}\quad$ D. $L^{2}MT^{-3}I^{-3}\quad$
2. 简答题
- (12 分)一时钟以恒定速度相对观测者运动,时间膨胀效应大小是否和时钟接近观测者或远离观测者有关?为什么?
- (10 分)利用磁偏转质量分析器可以将不同荷质比的带点粒子区分开。如下图所示,假设静止的带电粒子质量为 $m$,所带电荷量为 $q$,经过均匀静电加速后,从 $S_{1}$ 处垂直进入分析器的真空主体腔,腔体内有垂直于纸面的均匀静磁场。粒子在静磁场中飞行一段时间后,从 $S_{2}$ 处垂直射出,并被接收器探测到。假设 $S_{1}$ 和 $S_{2}$ 的间距为 2r。请问
(1) 当测量粒子带正电荷时,磁场方向应该垂直于纸面朝外还是朝内?
(2) 均匀加速静电场的电势差为 $U$,静磁场的磁感应强度为 $B$,写出探测到的带电粒子荷质比 $\frac{q}{m}$ 于 $U$ 和 $B$ 的关系表达式。
图 3:简答题 2 图示 - (8 分)在透明基地表面沉积一层折射率为 $n$ 的光学薄膜,可以制备成干涉滤光片。请简述干涉滤光片的原理,并给出透射光的波长 $\lambda_{0}$ 与该光学薄膜厚度 $l$ 及折射率 $n$ 的关系。
3.
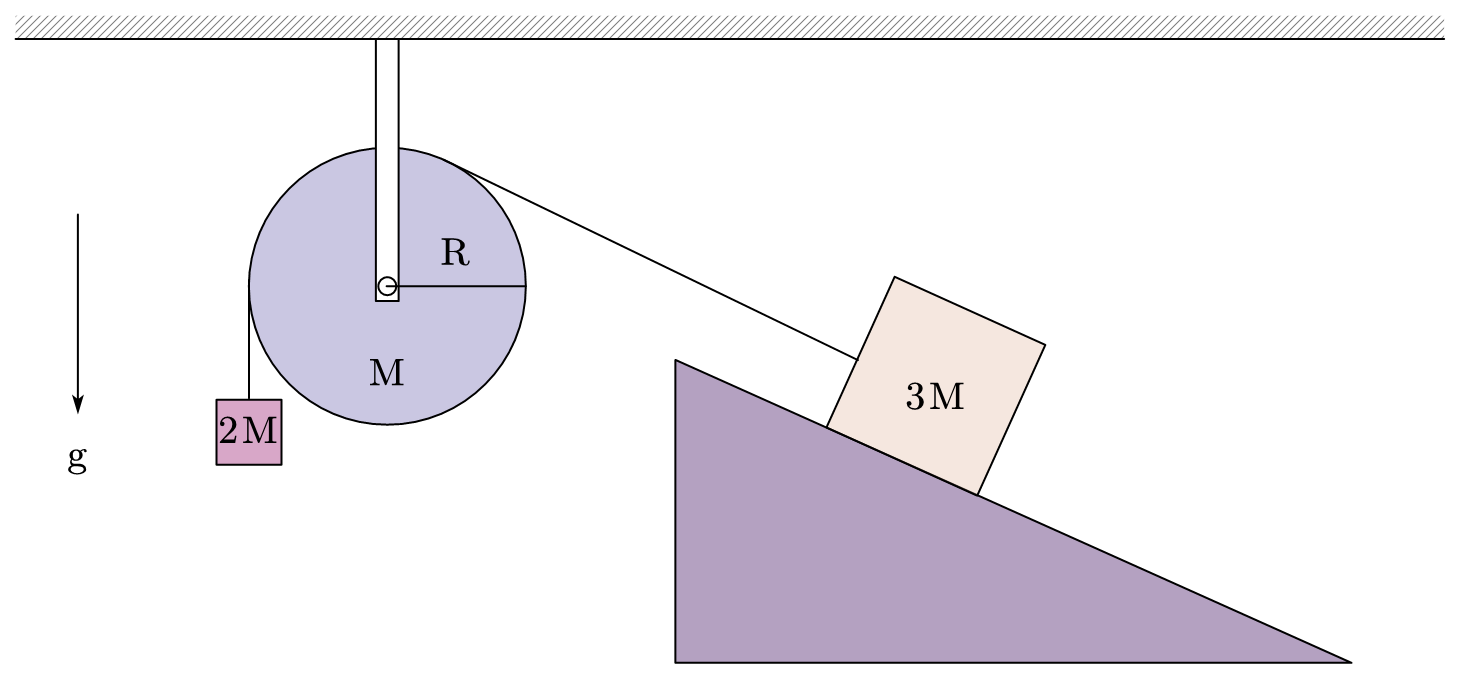
(共 20 分)如下图所示,一个阿特伍德机包含两个质量分别为 $2\mathrm{M}$ 和 $3\mathrm{M}$ 的物体,由一根无重量、无弹性的绳子连结并经过一个质量均匀分布的定滑轮。设滑轮的质量为 $\mathrm{M}$,半径为 $\mathrm{R}$,滑轮与绳之间的摩擦力以及滑轮与轴之间的摩擦力忽略不计,并且绳与滑轮之间无相对滑动。在初始状态,左边质量较轻的物体悬离地面,右边较重的物体被放置在一个斜坡上。斜坡与水平面的夹角为 $\theta$,斜坡表面与物体表面的摩擦系数为 $\mu$(忽略静摩擦与动摩擦的差异)。
(1)分别给出使得左边较轻的物体 $(i)$ 向上和 $(ii)$ 向下运动所需要满足的斜坡夹角 $\theta$ 以及摩擦系数 $\mu$ 的关系式(无需解出具体的 $\theta$ 值),并画出这两种情况下两个物体和滑轮分别的受力图。
(2)假设斜坡夹角 $\theta$ 以及摩擦系数 $\mu$ 满足使左边较轻的物体向下运动的条件,给出其对应的加速度表达式。
4.
(共 20 分)一根长为 $2L$ 的轻质刚性细杆位于水平的光滑桌面上,杆的两端分别固定一个质量为 $m$ 的小物块 $A$ 和一个质量为 $2\mathrm{m}$ 的小物块 $B$,杆可绕通过小物块 $B$ 所在端的竖直固定转轴在桌面上转动。一个质量为 $m$ 的小滑块 $C$ 套在细杆上($C$ 与杆密接),可沿杆滑动,环 $C$ 与杆之间的摩擦可忽略。一根轻质弹簧原长为 $L$,弹性系数为 $k$,两端分别与小环 $C$ 和物块 $B$ 相连。一个质量为 $m$ 的小滑块 $D$ 在桌面上以垂直于杆的速度飞向物块 $A$,并与之发生完全弹性碰撞,碰撞时间极短。碰撞前一瞬间,物块 $A$ 处于静止状态,小环 $C$ 恰好静止在距轴为 $r(r>L)$ 处。
(1)若碰撞前滑块 $D$ 的速度为 $v_{0}$,求碰撞过程中轴受到的作用力的冲量;
(2)若碰后物块 $A$、$C$ 和杆刚好做匀速转动,求碰前滑块 $D$ 的速度 $v_{0}$ 应满足的条件。
5.
(共 20 分)一不带电的圆球形肥皂泡半径为 $r$,肥皂水的表面张力系数为 $\alpha$(肥皂泡的厚度可忽略,则肥皂泡的表面能为 $2 \alpha S$,$S$ 为表面积),肥皂泡外大气压强为 $p$。使这肥皂泡均匀带上电荷量 $q$ 后,它的半径增大为 $R$,带电前后温度不变。求
(1)肥皂泡表面的电势以及系统的静电能;
(2)肥皂泡单位面积上所承受的静电力大小及方向;
(3)肥皂泡半径 $R$ 与所带电荷量 $q$ 所满足的关系。
6.
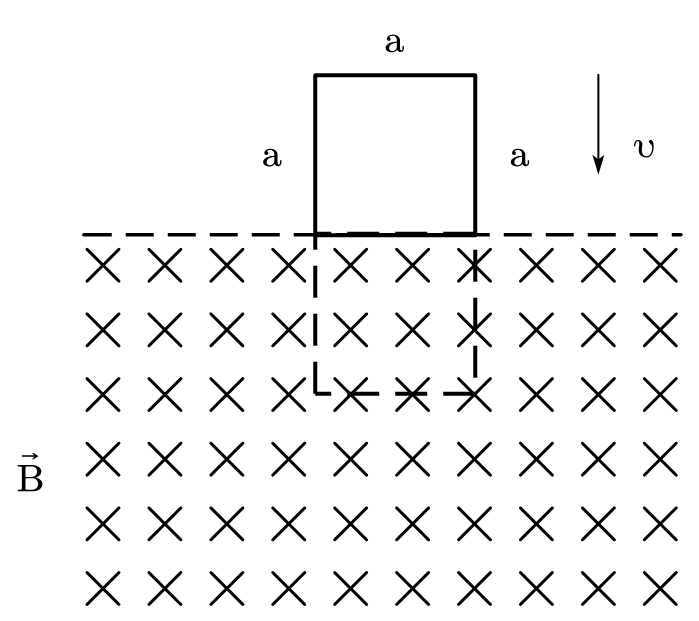
(共 20 分)如图所示,空间存在水平方向的磁感应强度 $B$ 的均匀磁场,且磁场存在一水平上边界(虚线所示)。空间中有一边长为 $a$ 的正方形细导线框,框面与磁场方向垂直,框的下边平行并紧贴磁场边界。导线框质量为 $m$,电阻为 $R$。忽略导线框的自感。导线框从起始位置垂直边界向下运动,直至刚刚完全浸入磁场区域的虚线位置。请问
(1)如果此过程在一个向上的外力作用下,线框维持匀速 $v$ 向下运动至虚线位置,那么给出该过程中导线框的电流总焦耳热;
(2)给出过程(1)中外力大小和总做功的大小;
(3)如果没有外力参与,线框从起始位置无初速度下落到虚线位置过程中,给出导线框的速度随时间的变化。
7.
(共 8 分)2016 年,LIGO 首次直接探测到引力波,其所使用装置类似于迈克耳孙干涉仪。一旦有引力波穿过装置,会导致两个光路的光程发生改变,干涉现象也随之改变,从而认为探测到引力波。具体说,由于两个光路的光程差发生改变,可以观测到干涉环在中心的吞吐现象:或者干涉环向中心收缩,或者干涉环从中心冒出。请问
(1)如果看到干涉环在中心冒出,这时两个光路的光程差的大小是增大还是减小?视场中的干涉环是越来越密集还是越来越稀疏?
(2)如果光程差改变 $0.25\mathrm{mm}$,那么会看到中心处条纹移过的数目为 909 个。求此时所用光源的波长?
(3)该实验使用两种手段改善实验效果:一种是采用强度很强的激光,二是隔离震动干扰。请问这两种实验手段中,哪个可以增加干涉条纹的亮度?哪个可以增加干涉条纹的对比度?