相机标定
编辑相机标定指的是求解相机的参数即成像模型参数的过程。相机的几何成像模型决定了三维空间物体表面的点与二维图像中对应点的变换关系,因此相机标定过程是三维重建中必不可少的步骤。相机参数包括了主点和焦距等与相机内部结构相关的内部参数,还包含了与相机旋转和平移等位置相关的外部参数[1]。随着三维重建技术的广泛应用使得相机标定方法的研究成为了一个研究的热点,简单、快捷和高精度的相机标定方法是研究相机标定技术追求的方向。
目录编辑
1 概述编辑
随着计算机视觉技术的发展,三维重建技术在机器人视觉、工业制造、工程建筑、文物保护和医疗等领域得到广泛应用。三维重建即是通过运用二维图像中的基本信息来恢复三维空间信息,而要从二维的图像信息中获取三维空间信息,也就需要研究二维图像中的点、线、面的二维坐标与三维空间中对应的点、线、面之间的对应关系,从而对空间物体的大小和位置关系进行定量分析。因此在三维重建中相机标定是不可或缺的步骤。
相机标定过程中需要对相机的内部参数和外部参数进行估计,即估计相机的几何参数和光学参数,还有相机相对于世界坐标系的空间位置和方向的参数。这些参数会直接影响到计算机视觉中获取到的三维空间信息的计算结果。目前能够达到实际使用并获得商业用途的三维形状信息获取技术中,主要有激光扫描、光飞跃时间、结构光扫描和 CT 等几种技术,但这些方法存在一些问题,如需要精密的设备、昂贵的价格以及获取的速度慢等问题。数码相机采用CCD 或 CMOS 代替传统银盐感光材质,将图像信息通过光电转换及数字处理,在存储器里得到的图像信息是以数码的形式存在的,其获取图像信息方便、快捷,普通的数码相机的价格不贵并且在不断的下降。相机的标定已成为计算机视觉方面的一个重要的研究方向[2]。
2 针孔成像模型编辑
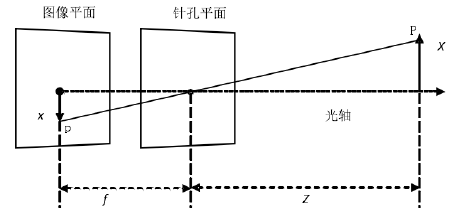
相机成像模型可以通过对光学成像模型的简化来确定,目前存在线性和非线性两种成像模型,相机实际的成像过程上是非线性的。小孔成像模型是相机成像系统中运用最多的模型(图1所示)。物体的三维空间坐标和图像坐标是线性的关系,因此估计相机参数的过程就在于求解线性方程组上。
从图1 可以看出,相机的光轴与图像平面垂直,其中𝑓为相机的焦距,𝑍为相机到物体之间的距离,𝑋是物体的长度,𝑥是物体在图像中对应的长度。根据相似三角形原理,有𝑥/𝑓 = −𝑋/𝑍。为了便于理解,在计算时一般假设图像平面位于针孔平面和物体之间,这样就可以得到目标图像不再为倒立的关系表达式: 𝑥/𝑓 = 𝑋/𝑍。3 坐标系转换模型编辑
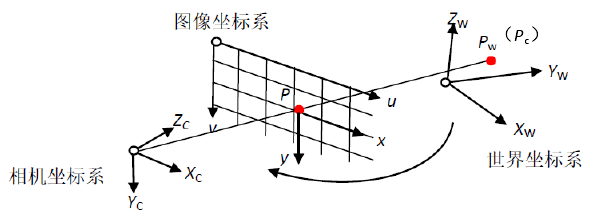
相机的成像模型中用到了三个不同的坐标系,分别为图像坐标系、相机坐标系和世界坐标系。假设世界坐标系中一点 


3.1 图像坐标系
图像坐标系是相机拍摄的图像的坐标系,其有像素单位和物理单位两种表达方法,意义分别表述如下:
像素坐标系:规定其原点位于图像的右上角,坐标轴分别为 u 轴和 v 轴,单位为像素。
物理坐标系:规定其原点为相机镜头光轴与图像坐标系下 uv 平面的交点,坐标轴为 x 轴和 y 轴,单位为米。 这两种坐标系的转换关系如式(2-1)所示:

其中

3.2 相机坐标系
以相机光心(可看作为镜头透镜的中心)为坐标系的原点,以相机的光轴作为



其中 f 为相机焦距。上式可用齐次坐标的矩阵形式表示为:

3.3 世界坐标系
世界坐标系是客观三维空间的绝对坐标系,也叫做客观坐标系。相机在三维空间中的位置通过建立世界坐标系来确定,确定相机位置的同时也确定了三维空间中目标物体的位置。相机坐标系与世界坐标系之间的转换关系为:

其中𝑅是 3×3 的旋转矩阵,𝑡是平移向量。综合式(2-2)、(2-4)、(2-5)可得:

经简化后可得:

其中𝑠为一个任意尺度比例,


4 镜头畸变模型编辑
在理想情况下,由式(2-7)可知,给定一个拥有足够数量的点集合,并且知道它们在世界坐标系下的坐标和对应的像素坐标系下的坐标,就可以解出相机的内外参数。但是在加工生成过程中,限于材料和工艺水平等因素,相机镜头并不是理想的光学成像系统。而且,在透镜的安装过程中,也很难保证透镜与成像感光芯片保持平行。因此,在用相机拍照时,实际成像点与理想的位置往往存在一定的偏差[4]。
4.1 径向畸变
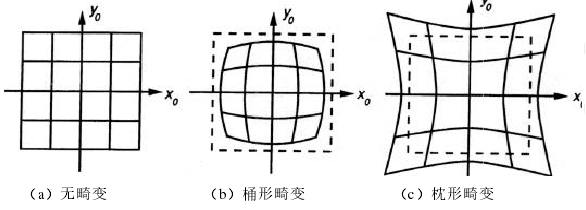
径向畸变只是由于相机镜头的透镜形状不理想所致实际的成像点的位置相对于理想位置沿径向产生偏移的现象。径向畸变可以分为桶形畸变和枕形畸变:
桶形畸变:视野中光轴中心附近区域放大率远大于边缘区域,如图 3(b)所示。常出现于广角镜头和鱼眼镜头。
枕形畸变:又称鞍形畸变,同桶形相反,视野中边缘区域的放大率远大于光轴中心附近区域放大率,如图 3(c)所示。常出现在远摄镜头中。
4.2 切向畸变
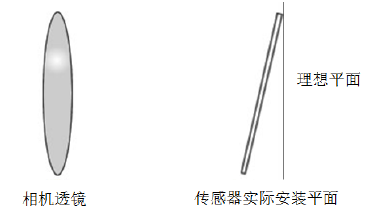
切向畸变是指由于透镜本身与相机传感器平面(成像平面)不平行而导致的线性畸变。这种情况多是因为在将透镜粘贴到镜头模组上时的安装偏差所引起,如图4所示。
4.3 实际相机成像模型
针孔成像模型是理想的透视模型,物和像之间满足相似三角形的关系。实际的情况是相机的光学系统存在畸变,透镜的物和像之间不满足相似三角形的关系。我们假设世界坐标系下有一点,其在考虑畸变情况的相机图像坐标系里的物理坐标为


其中


其中



5 标定方法分类编辑
相机标定的概念最先是源于摄影测量学,在对摄影测量学机器视觉领域的不断研究过程中,许多学者对相机标定也进行了深入的研究,并且提出了不同的相机标定方法。以标定方法中是否使用标定参照物来分类,可以从广义将相机标定方法分为传统相机标定方法、相机自标定方法和基于主动视觉的标定方法。
5.1 传统相机标定方法
传统的相机标定方法有很多学者提出了不同的算法思路,传统的相机标定方法根据算法的不同思路又可分为以及基于最优化算法的相机标定方法、基于相机变换矩阵的相机标定方法以及考虑了畸变补偿的其他方法。
1) 基于最优化算法的相机标定方法
利用最优化算法进行相机标定的方法假设相机成像的光学模型非常复杂,这是这类方法的一个优点。这类相机标定方法求得相机标定参数的结果受参数给定的初始值的影响,同时优化步骤也非常的耗时,假如给定的参数初始值不理想的的话,优化过程很难得到准确的参相机数结果,耗时的优化程序也无法得到实时的结果。根据参数模型的选取不同,这类算法的主要有摄影测量学中的传统方法和直接线性变换法。
摄影测量学中的传统方法典型代表方法是 Faig[5]提出来的方法,该标定方法建立一个很复杂的相机成像模型,建立相机模型的过程中不仅利用了针孔相机模型的共面约束条件,还考虑到了成像过程中各种因素对成像的影响。标定方法描述每一幅图像的空间约束关系至少利用了 17 个参数,因而计算量相当的大。
直接线性变换法是 Abde1.Aziz 和 Karara 在 1971 年提出的[6],这种方法求解相机的参数结果精度不高,因为算法忽略了相机成像过程中分线性的因素,相机的镜头畸变也没有考虑,标定相机模型的各个参数是通过求解线性方程来获得的。
2)基于透视变换矩阵的标定方法
该种相机标定用一个非线性的方程来描述三维世界坐标系与二维图像像素坐标系之间的变换关系,其中非线性的方程包含了相机模型的内外参数。在不考虑相机镜头畸变等分线性的约束条件的情况下,同时把透视变换矩阵中的元素当作未知数,可以运用一组三维空间点和图像对应点的对应信息来线性的求解矩阵中的元素的值。
3)Tsai 两步法
Tsai 提出的两步法是基于径向一致约束的方法[7],求解参数分为两步,根据径向一致约束条件,可以先求解出一部分相机成像模型的参数,再通过非线性优化步骤得到相机模型其他参数的值。这种方法在工业视觉系统中运用比较多,径向一致约束法这种方法获得的标定结果精度比较高,使用与需要精密测量的场合。径向一致约束法求解相机模型参数的过程中大部分方程式线性方程,降低了求解参数的复杂度,标定过程速度快、准确。但不适合普通的标定场景,因其需要高精度的标定设备作为代价。
4)张正友标定法
张正友[8]在 1998 年提出了一种比较简单灵活的方法,该方法是介于传统方法和自标定方法之间的一种方法,该方法假定平面标定板置于其所在的世界坐标系Zw=0 的平面上,其通过线性成像模型来求得相机参数的初值,然后基于非线性成像模型给出考虑了非线性畸变的目标函数,然后使用非线性最优化的方法来获得相机参数的最优解。这种标定方法具有较好的鲁棒性、实用性和较高的精度,避免了传统方法需要高精度设备的要求。不足之处在于线性估计相机参数初值是采用的是整幅图像的像点,不能为非线性求解过程提供一个较理想的初始值。
5.2 相机自标定法
相机自标定法标定相机仅需要用到相机运动过程中多幅环境图像之间的对应关系,并不需要特定的标定参照物。相对于传统的相机标定方法,其算法不足之处在于鲁棒性较差,但由于标定过程不需要标定参照物,所以算法更加的灵活,对于未知场景和相机运动任意的情况下也可以对相机进行标定。目前已而言,有基于 Kruppa 方程的自标定方法和基于二次曲面的自标定法,还有分层逐步标定法等自标定方法。
1)基于 Kruppa 方程的自标定方法
Faugeras[9]等对射影几何的研究证明了每两幅图像间存在两个形如 Kruppa 方程的二次约束,内部参数可以通过求解 Kruppa 方程组来确定。基于 Kruppa 方程的自标定方法标定相机的过程仅需要建立两幅图像之间的方程,对图像序列的摄影重建过程并不考虑。如果图像序列较长,且所有图像相对于确定的射影空间的无穷远平面一致性无法保证,标定算法的稳定性会受到影响。
2)基于二次曲面的自标定法
将绝对二次曲面引入相机标定的过程中,从本质上来说,其与基于 Kruppa 方程的标定方法是一直的概念,最先是由 Triggs[10]提出来的。都是根据欧式变换下的绝对二次曲线的不变性质来进行的。相对于基于 Kruppa 方程的自标定方法,基于绝对二次曲面的自标定法不仅包含了二次曲线的信息,还包含了无穷远平面的信息。标定方法计算二次曲面之前先对图像做了射影重建,因此对所有图像的无穷远平面的一致性就得到了保证,所以基于二次曲面的自标定法更加的稳定。
3)分层逐步标定
分层逐步标定法做相机标定之前,与基于二次曲面的自标定法一样要对图像序列做射影重建步骤,在重建图像序列的基础上接着进行放射标定和欧式标定。通过将所有图像与其中一幅图像做摄影对齐,减少了未知数的个数,应用非线性优化算法将所有的未知数同时求出。优化算法的收敛性不确定是这类标定方法的一个缺点,因为优化初始值只能估计,同时重建图像序列的射影对齐的参考图像是不确定的,不同的参考图像会使得相机参数标定结果不一样。
5.3 基于主动视觉的相机标定法
基于主动视觉的相机标定方法是在已知相机的某些运动信息的情况下进行标定相机的,这些信息有定性的和定量的,由于知道了一些相机的运动信息,基于主动视觉的相机标定方法求解相机的参数是线性的,所以算法具有较高的鲁棒性。基于主动视觉的相机标定法中的相机可以知道其精确的运动信息,通过控制相机运动的控制平台控制相机运动拍摄多幅图像,相机的内参数和外参数可以通过图像信息和相机的运动信息求得[11]。该种算法需要精准的相机运动平台,标定不够灵活是一个不足的方面。
6 经典标定方法——张正友法编辑
在 1998 年,张正友提出了一种基于棋盘格模板的相机标定方法成为相机标定研究的经典方法。这种方法分为两个步骤。一是对相机参数进行初始估计,二是通过优化函数对参数进行迭代求精。
6.1 相机参数的初始估计
假设标定目标位于世界坐标系 Z=0 的平面上,则图像坐标系中的点𝑃(𝑢,𝑣)和其在世界坐标系中对应的点𝑃𝑤(𝑋,𝑌,𝑍)之间的关系可以根据式(2-7)表述为:
(5-1)
其中。在已知点在世界坐标系下的坐标和对应的像素坐标系下的坐标的情况下,H 可以用最小二乘法求出。由于旋转矩阵𝑅具有
和
的性质,故每一幅标定图像对相机内参矩阵产生两个约束条件:
(5-2)
令:
(5-3)
由于 B 是对称矩阵,所以可以写成一个 6 维向量形式:
(5-4)
则可以计算得:
(5-5)
其中为矩阵 H 的第 i 列,
。
利用公式 3-2 的约束条件可以得到方程组:
(5-6)
如果在不同的位置拍摄了 n 幅图像,则可以获得与式(5-6)类似的 n 个方程,将其组合后可得:
(5-7)
由于 b 是一个 6 维向量,由线性代数的知识可知,当 n≧3 时,b 存在唯一解。所以,要完成相机标定至少需要拍摄三张图像,而且图像不能平行于相机的光轴。对式(5-7)进行求解以后,可以得到一个满足最小二乘的向量 b,进而可以解得相机内参矩阵 A。将内参数代入式(5-2)即可得到如下相机外参数:
(5-8)
6.2 参数优化求精
在理想的情况下,像素坐标系下的坐标与三维空间点的坐标通过所求出的相机参数矩阵投影到像素坐标系是同一个点,但在实际的情况下会存在误差,所以为了得到更加精确的相机参数,可以通过下面的投影误差最小化函数来对相机参数迭代求精[12]。
(5-9)
其中,,表示空间中点
投影到第 i 幅二维图像的坐标,
表示标定板的第 i 幅二维图像中第 j 个投影点的坐标,
分别表示标定板的第 i幅二维图像的旋转和平移参数。
参考文献
- [1]
^三维重建中的相机标定方法研究_冯焕飞[J]. .
- [2]
^夏仁波, 刘伟军, 赵吉宾, 徐金亭. 基于圆形标志点的全自动相机标定方法[J]. 仪器仪表学报 , 2009,(02)..
- [3]
^机器视觉和图像技术[J]. 自动化博览 , 2009,(02)..
- [4]
^基于多个深度相机的足部三维重建及形态分析_毋戈[J]..
- [5]
^Faig W·Calibration of close-range photogrammetric systems : mathematical formulation. Photogram metriceng[J].Remotesensing,1975.41(12):1479~1486. .
- [6]
^A bdel-A ziz YI, Karara HM. Direct linear transformation into object space coordinates in Close-Range Photogrammetry[A]. ProcSymp[C]. Close-Range Photogrammetry. 1971. 1-18..
- [7]
^Tsai. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE Journal of robotics and automation,1987,Vol. RA-3(4):323-344. .
- [8]
^Z.Zhang, Flexible camera calibration by viewing a plane from unknown orientations[C].Proceedings of the 7th International Conference on Computer Vision, 1999:666-673..
- [9]
^Zhang ZY. Camera calibration with one-dimensional objects[J]. IEEE-T PAMI,2004,26(7):892-899. [16] Y. I. Abdel-Aziz , H. M. Karara. Direct linear transformation into object space coordinates in close-range photogrammetry[C]. Proc. Symp. Close-Range Photogrammetry, Urbana-Champaign, IL, 1971:1–18. .
- [10]
^Triggs B, Auto—calibration and absolute quadric[A]. Proceedings of Computer Vision and PatternRecogintiong[C],1997,604-614. .
- [11]
^Ma S D.A self-calibration technique for active vision system[J].IEEE Trans.Robotics and Automation.1996.2. .
- [12]
^凌丹,黄洪钟等.混合威布尔分布参数估计的 L-M 算法[J].电子科技大学学报,2008.7. .
暂无