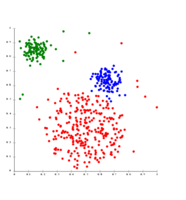
聚类分析

“聚类”的概念无法精确定义，这也是为什么有这么多聚类算法的原因之一。 它们有一个共同点:都是一组数据对象。然而，不同的研究者会使用不同的聚类模型，并且对于这些聚类模型中的每一个，同样可以给出不同的算法。由不同的算法发现，集群的概念在其属性上有很大的不同。理解这些“聚类模型”是理解不同算法之间差异的关键。典型的集群模型包括:

• 连通性模型 ：例如，分层聚类基于距离连通性来构建模型。
• 质心模型 ：例如，k-means算法用单个均值向量表示每个聚类。
• 分布模型 ：聚类是使用统计分布建模的，例如由期望最大化算法使用的多元正态分布。
• 密度模型 ：例如，DBSCAN和OPTICS将集群定义为数据空间中连接的密集区域。
• 子空间模型 ：在双聚类(也称为共聚类或双模聚类)中，聚类由聚类成员和相关属性建模。
• 组模型 ：有些算法不提供精确的结果模型，只提供分组信息。
• 图模型 ：一个集团，即图中节点的子集，令该子集中的每两个节点通过一条边连接，可以认为这是聚类的原型。完全连通性要求的松弛(一部分边缘可能丢失)被称为准派系，如HCS聚类算法。
• 神经网络模型 ：最著名的无监督神经网络是自组织映射，这些模型通常可以被描述为类似于上述模型当中的一个或多个，并且当神经网络实现一种形式的主成分分析或独立成分分析的形式时，子空间模型也会被包括在内。

“聚类”本质上是一组这样的聚类，它通常包含数据集中的所有对象。此外，它可以指定集群彼此之间的关系，例如，彼此嵌入的集群的层次结构。聚类可以大致区分为:

• 硬聚类 ：每个对象是否属于一个集群
• 软聚类 (同时: 模糊聚类 ):每个对象在一定程度上属于每个集群(例如，属于集群的可能性)

还有更细微的区别，例如:

• 严格分区聚类 ：每个对象恰好属于一个集群
• 带有野值的严格分区聚类 ：对象也可以不属于任何集群，并且被视为野值
• 交叠聚类 (同时: 替代聚类, 多视图聚类 ) ：对象可能属于多个集群；通常涉及硬聚类
• 分级聚类 ：属于子聚类的对象也属于父聚类
• 子空间聚类 ：虽然交叠聚类在唯一定义的子空间内，但聚类不应该重叠

如上所列，聚类算法可以根据它们的聚类模型进行分类。以下概述将仅列出聚类算法的最突出的例子，因为可能有超过100种已发布的聚类算法。不是所有的聚类算法都会为它们的集群提供模型，因此不容易分类。维基百科解释的算法概述可以在统计算法列表中找到。

现在这里没有客观“正确”聚类算法，但是正如所指出的，“聚类是旁观者的眼睛。”^[5] 对于一个特定的问题，最合适的聚类算法通常需要通过实验来选择，除非有数学上的原因使一个聚类模型优于另一个。应该注意的是，为一种模型设计的算法通常会在包含完全不同类型模型的数据集上失败。^[5] 例如，k-means算法找不到非凸集群。^[5]

2.1 基于连通性的聚类(分层聚类)

基于连通性的集群，也称为 分层聚类，是基于一个核心概念，即物体与附近物体的关系比与远处物体的关系更密切。这些算法根据“对象”的距离将它们连接起来形成“集群”。集群很大程度上可以用连接集群的各个部分所需的最大距离来描述。在不同的距离，将形成不同的聚类，这可以用树图来表示，树图解释了通用名称“分层聚类”的来源:这些算法不提供数据集的单一划分，而提供了在特定距离彼此融合的广泛的聚类层次。在树形图中，y轴表示集群融合的距离，而对象沿着x轴放置，这样集群就不会混淆。

基于连通性的聚类是一整套以距离计算方式为区别的方法。除了通常选择的距离函数，用户还需要决定要使用的链接标准(因为一个集群由多个对象组成，所以有多个候选对象来计算距离)。一般通用的选择被称为单链聚类(最小物距)、完全连锁聚类(最大物距)和UPGMA或WPGMA(“具有算术平均的未加权或加权对组方法”，也称为平均链聚类)。此外，层次聚类可以是聚集(从单个元素开始，然后将它们聚集成集群)或分裂的(从完整的数据集开始，然后将其划分成分区)。

这些方法不会产生数据集的唯一分区，但是用户仍然需要从中选择适当集群的层次结构。它们对于野值的表现不是很稳定，野值要么会显示为额外的集群，要么甚至会导致其他集群合并(称为“链式现象”，特别是单链聚类)。在一般情况下，对于聚集聚类，复杂性是    ，且对于分裂聚类，复杂性是   ，^[5] 这使得它们的处理速度对于大型数据集来说太慢。对于某些特殊情况，我们有已知的最佳有效方法(复杂性   ):用于单链聚类的SLINK^[6] 和用于完全连锁聚类的CLINK^[7] 。在数据挖掘社区，这些方法被认为是聚类分析的理论基础，但通常被认为是过时的。然而，它们确实为许多后来的方法提供了灵感，例如基于密度的聚类。

• 链接聚类的例子

• 

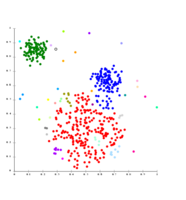
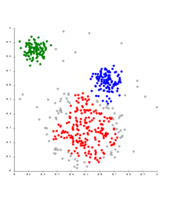
  高斯数据上的单链接。在35个聚类中，最大的聚类开始分裂成更小的部分，而在此之前，由于单链效应，它仍然连接到第二大聚类。

• 

  基于密度的聚类上的单链接。提取了20个聚类，其中大部分只包含单个元素，因为链接聚类没有“噪声”的概念。

2.2 基于质心的聚类

在基于质心的聚类中，聚类由中心向量表示，该向量不一定是数据集的成员。当集群数量固定为 k, k-均值聚类给出了优化问题的正式定义:找到 k 聚类中心，并将对象分配到最近的聚类中心，使得离聚类的平方距离最小化。

优化问题本身被称为NP难题，因此常用的方法是只搜索近似解。一种特别著名的近似方法是劳埃德算法，^[8] 通常简称为"k均值算法"(尽管另一种算法也采用了这个名称)。然而，它只会找到一个局部最优值，并且通常会以不同的随机初始化操作运行多次。k 均值算法的各种变体通常包括一些优化，例如选择多个运行中的最佳运行的同时，还将质心限制在数据集的成员(k-中心点算法)，选择中值(k-中心聚类)，减少对于初始中心的随机选择(k-means++)或允许模糊聚类分配(模糊c-均值)。

大部分k-均值类型算法需要预先指定集群数量–k ，这被认为是这些算法的最大缺点之一。此外，这些算法更适合大小近似的聚类，因为它们总是将对象分配到最近的质心。这导致聚类边界经常被错误地切割(这并不奇怪，因为该算法优化聚类中心，而不是聚类边界)。

K-均值算法有许多有趣的理论性质。首先，它将数据空间划分成一个沃罗诺伊图的结构。其次，它在概念上接近最近邻分类，因此在机器学习中很流行。第三，它可以被看作是基于模型的聚类的变体，劳埃德算法是下面讨论的该模型的期望最大化算法的变体。

• ''k''-均值聚类举例

• 

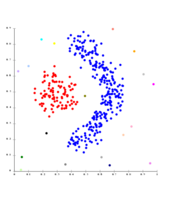
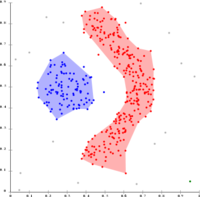
  k 均值算法将数据分离到Voronoi单元中，该单元假设聚类大小相同（此图不满足假设）

• 

  k 均值算法不能用于表示基于密度的聚类

2.3 基于分布的聚类

与统计最密切相关的聚类模型是以分布模型为基础的。聚类很容易被定义为最有可能属于同一分布的对象。这种方法的一个方便的特性是，它非常类似于人造数据集的生成方式:从一个分布中采取随机对象作为样本。

虽然这些方法的理论基础很好，但是，除非我们去限制模型的复杂性，不然它们就会遇到一个称为过拟合的关键问题。一个更复杂的模型通常能够更好地解释数据，这使得选出合适的模型复杂性这件事本身就是困难的。

有一种效果突出的方法被称为高斯混合模型(使用期望最大化算法)。在这里，数据集通常以固定(避免过拟合)数量的高斯分布建模，这些高斯分布被随机初始化，并且其参数被迭代优化以更好地适应数据集。这将收敛到局部上的最优解，所以多次运行可能会产生不同的结果。为了获得硬聚类，对象通常被分配到它们最可能属于的高斯分布；对于软集群，这不是必需的。

基于分布的聚类产生了复杂的聚类模型，可以捕捉属性之间的相关性和依赖性。然而，这些算法给用户带来了额外的负担:对于许多真实数据集，可能没有简明定义的数学模型(例如，假设高斯分布是一个对数据的相当强的假设)。

• 高斯混合模型聚类举例

• 

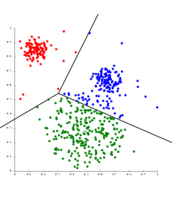
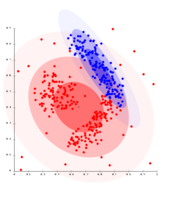
  在高斯分布的数据上，EM的运行效果很好，因为它使用了高斯方法对聚类进行建模

• 

  基于密度的聚类不能使用高斯分布来建模

2.4 基于密度的聚类

在基于密度的聚类中，^[9] 聚类被定义为密度高于数据集其余部分的区域。这些稀疏区域中的对象——这些对象需要去分离聚类——通常被认为是噪声和边界点。

最受欢迎的^[10] 基于密度的聚类方法是DBSCAN。^[11] 与许多更新的方法相比，它具有一个被称为“密度可达性”的定义明确的聚类模型。类似于基于链接的聚类，它基于特定距离阈值内的连接点。但是，它只连接满足密度标准的点，在原始变体中定义为该半径内的最小数量的其他对象。一个集群由所有密度连接的对象(与许多其他方法不同，它可以形成任意形状的集群)加上这些对象范围内的所有对象组成。DBSCAN的另一个有趣的特性是它的复杂性相当低——它需要在数据库上进行线性数量的范围查询——并且它将在每次运行中发现本质上相同的结果(它对于核心点和噪声点是确定性的算法，但对于边界点不是)，因此不需要多次运行它。OPTICS ^[12] 是DBSCAN的一个归纳，它不需要为范围参数   选择合适的值，并且它会产生与链接聚类相关的分层结果。DeLi-Clu，^[13] 即密度-链接-聚类算法结合了单链接聚类和OPTICS的思想，完全消除了    参数，并通过使用R树索引提供优于OPTICS的性能改进。

DBSCAN和OPTICS的主要缺点是它们期望由某种密度的下降来检测聚类边界。例如，在重叠高斯分布的数据集上——人工数据中的一个常见用例——这些算法产生的聚类边界通常看起来是任意的，因为聚类密度会不断降低。在由高斯混合模型组成的数据集上，诸如EM聚类等能够精确建模这种数据的方法几乎总是优于这些算法。

均值漂移是一种聚类方法，根据核密度估计，在这个运行的算法之下，每个对象将被移动到其附近密度最大的区域。最终，对象会收敛到密度的局部最大值。类似于k-均值聚类，这些“密度吸引子”可以作为数据集的代表，但是均值漂移可以检测类似于DBSCAN的任意形状的聚类。由于具有昂贵成本的迭代过程和密度估计，均值漂移通常比DBSCAN或k均值算法慢。此外，均值漂移算法对多维数据的适用性会受到核密度估计不平滑行为的阻碍，这导致了簇尾的过度分裂。^[13]

• 基于密度的聚类举例

• 

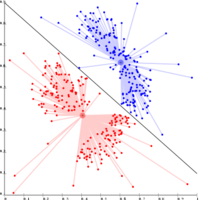
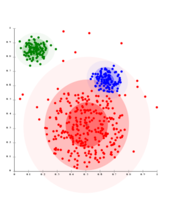
  基于密度的DBSCAN聚类

• 

  DBSCAN假设集群具有相似的密度，并且可能在分离附近的集群时存在问题

• 

  OPTICS是一种DBSCAN变体，改进了对不同密度集群的处理

2.5 最近的发展

近年来，在改进现有算法的性能方面人们已经付出了相当大的努力。^[14][15] 其中包括CLARANS (Ng和Han, 1994),^[16]和BIRCH (Zhang et al., 1996).。^[17] 随着最近对于处理越来越大的数据集(也称为大数据)的需求，人们越来越愿意用生成的集群的语义来交换性能。这导致了预聚类方法的发展，例如冠层聚类，它可以有效地处理巨大的数据集，但是产生的“聚类”仅仅是数据集的粗略预划分，然后用现有的较慢的方法(例如k-均值聚类)来分析分区。

对于高维数据，许多现有的方法由于维数灾难而失败，这使得特定的距离函数在高维空间中存在问题。这导致了针对高维数据的新的聚类算法的产生，该算法侧重于子空间聚类(其中仅使用一些属性，并且聚类模型包含聚类的相关属性)和相关聚类，该算法还寻找任意旋转(“相关”)的子空间聚类，该子空间聚类可以通过给出其属性的相关性来建模。^[18] 这种聚类算法的例子是CLIQUE^[19] 和SUBCLU^[20]。

基于密度的聚类方法(特别是DBSCAN/OPTICS系的算法)的思想已经被用于子空间聚类(HiSC，^[21] 分层子空间聚类和DiSH^[22])和相关聚类(HiCO，^[23] 分层相关聚类，4C^[24] 使用“相关连接“，ERiC^[25] 探索基于分层密度的相关聚类)。

几种不同的基于互信息的聚类系统已经被提出了。一种是玛丽娜·梅勒的信息的变化 度量；^[26] 另一种则提供分层聚类。^[27] 使用遗传算法，可以优化各种不同的包括互信息在内的拟合函数。^[28] 信息传递算法是计算机科学和统计物理的最新发展成果，它也导致了新型聚类算法的产生。^[29]

聚类结果的评估(或“验证”)和聚类本身一样困难。^[30] 流行的方法包括将聚类总结为单一质量分数的"内部 "评估，将聚类与现有“地面实况”分类进行比较的"外部 "评估，人类专家的"手动 "评估，以及通过评估聚类在预期应用中的效用的"间接 "评估。^[31]

内部评价措施的问题在于，它们代表的功能本身可以被视为一个聚类目标。例如，可以通过轮廓系数对数据集进行聚类；除了那以外再没有已知的有效算法来解决这个问题了。通过使用这种内部评估方法，它可以去比较优化问题的相似性，^[31] 但没有必要比较聚类用处的大小。

外部评估也有类似的问题:如果我们有这样的“地面实况”标签，那么我们就不需要聚类；但在实际应用中，我们通常没有这样的标签。另一方面，标签只反映了数据集的一种可能的划分，这并不意味着不存在不同的，甚至更好的聚类。

因此，这两种方法都不能最终判断聚类的实际质量，但这需要高度主观的人工评估^[31] 。然而，这种统计在识别不良聚类时可以提供大量信息，^[32] 但是我们不应该忽视人类的主观评价。^[32]

3.1 内部评估

当基于聚类本身的数据评估聚类结果时，这称为内部评估。这些方法通常会为，产生在聚类内相似性高、聚类间相似性低的聚类的算法，分配最佳分数。在聚类评估中使用内部标准的一个缺点是，内部度量上得出的高分不一定代表着有效的信息检索应用。^[33] 此外，这种评估偏向于使用相同聚类模型的算法。例如，k-means聚类自然地优化了对象距离，并且基于距离的内部标准可能会对结果聚类作出过高的评分。

因此，内部评估措施最适合深入了解一种算法比另一种算法表现更好的情况，但这并不意味着一种算法会比另一种算法产生更有效的结果。^[34] 用这种指标衡量的有效性取决于数据集内存在这种结构的事实。如果数据集包含一组完全不同的模型，或者如果评估衡量的标准完全不同，那么仅为某一种模型设计的算法就没有机会获得高分。^[34] 例如，k-均值聚类只能找到凸聚类，许多评价指标都以凸聚类为假设设定。在具有非凸聚类的数据集上，既不使用k均值，也不使用假定为凸性的评价标准，这都是合理的。

内部评估方法有十多种，它们通常是基于同一集群中的项目应该比不同集群中的项目更相似的直觉。^[34] 例如，以下方法可用于评估基于内部标准的聚类算法的质量:

• Davies Bouldin指数

Davies Bouldin指数可以通过以下公式计算:

   

n 是集群的数量，     是聚类    的质心,     是集群    中所有元素到质心    的平均距离，和     质心    和    之间的距离。由于产生低簇内距离(高簇内相似度)和高簇间距离(低簇间相似度)的聚类算法具有较低的Davies Bouldin指数，因此基于该准则，产生一组具有最小Davies Bouldin指数的聚类算法被认为是最佳算法。

• 邓恩指数

邓恩指数旨在识别密集和分离良好的聚类。它被定义为最小簇间距离与最大簇内距离之间的比率。对于每个集群分区，邓恩指数可以通过以下公式计算:       ^[35]  

     

d（ i, j )表示集群 i 和 j 之间的距离，和 d '( k ) 测量的是聚类 k 的簇内距离。在两个聚类之间的簇间距离 d（ i, j )可以是任意数量的距离度量，例如聚类的质心之间的距离。类似地，簇内距离 d '( k) 可以用多种方式测量，例如集群 k 中任意一对元素之间的最大距离。由于内部标准寻求具有高簇内相似性和低簇间相似性的聚类，所以产生具有高邓恩指数的簇的算法是更为理想的。

• 轮廓系数

轮廓系数将同一个聚类中元素的平均距离与其他聚类中元素的平均距离进行对比。轮廓值高的对象被认为是聚类良好的对象，而轮廓值低的对象可能是离群值。该指数适用于 k-均值群集，也用于确定群集的最佳数量。

3.2 外部评估

在外部评估中，聚类结果基于未用于聚类的数据进行评估，例如已知的类标签和外部基准。这样的基准由一组预先分类的项目组成，这些项目通常是由(专家)人类创建的。因此，基准集可以被视为评估的黄金标准。^[30] 这些类型的评估方法用于衡量聚类与预定基准类的接近程度。然而，这是否适用于实际数据，或者是否仅适用于具有事实基础事实的合成数据集等问题在近期被讨论过，因为类可以包含内部结构，存在的属性可能不允许聚类分离，或者类可能包含异常。^[36] 此外，从知识发现的角度来看，预期的结果不一定是已知知识的再现。^[36] 在约束聚类的特殊情况下，在聚类过程中已经使用了元信息(例如类标签)，出于评估目的的信息延迟不是微不足道的。^[37]

许多衡量标准都是根据用于评估分类任务的变量进行调整的。这类计数指标并非计算一个类被正确分配给单个数据点的次数(称为真阳性)，而是评估真正在同一集群中的每对数据点是否都被预测在同一集群中。^[30]

如同内部评估，外部评估措施也有若干个，^[34] 例如:

• 纯度:纯度是衡量聚类包含单一类别的程度。^[33] 它的计算可以认为如下:对于每个聚类，计算来自所述聚类中最常见类的数据点的数量。现在将所有聚类的总和除以数据点总数。形式上，给定一些聚类     和一些类    ，两个分区     数据点，纯度可以定义为:

     

请注意，这种方法不会对拥有许多聚类的情况造成不利影响。例如，通过将每个数据点放在它自己的簇中，可以获得纯度为1的分数。纯度也不适用于不平衡的数据:如果大小为1000的数据集由两个类组成，一个类包含999个点，另一个只有1个点。无论聚类算法的性能有多差，它都会给出非常高的纯度值。

• 兰德测量(威廉·兰德1971)^[38]

兰德指数计算聚类(由集群算法返回)与基准分类的相似程度。人们还可以将兰德指数视为算法做出正确决策的百分比的度量。可以使用以下公式计算:

   

    是真正阳性的数量，     是真正否定的数量，     是假阳性的数量，并且     是假阴性的数量。兰德指数的一个问题是假阳性和假阴性的权重相等。对于一些集群应用程序来说，这可能是不理想的特性。F-措施解决了这一问题， 机会修正后的兰德指数也解决了此问题。

• F-测量

F-测度可以通过参数    加权回收来平衡假阴性的贡献。设精确度和召回率(两个本身都是外部评估指标)定义如下:

   

   

    为精确率和     为召回率。我们可以使用以下公式计算F-测量:^[33]

   

注意什么时候    ,    。换句话说，当    ，召回对F-measure没有影响，并且在最后的F-测量中，    的增长会为召回分配越来越多的权重。

还要注意    不考虑在内且可以从0向上变化而没有界限。

• 杰卡德系数

杰卡德系数用于量化两个数据集之间的相似性。杰卡德系数的值介于0和1之间。指数为1表示这两个数据集是相同的，指数为0表示这两个数据集没有公共元素。杰卡德系数由以下公式定义:

   

这只是两组共有的唯一元素的数量除以两组中唯一元素的总数。

还要注意     不考虑在内，可以从0向上变化而没有界限。

• 骰子指数

骰子对称度量使    的权重加倍，同时仍然忽略    :

   

• Fowlkes–Mallows指数(E. B. Fowlkes & C. L. Mallows 1983)^[39]

Fowlkes–Mallows指数计算聚类算法返回的聚类和基准分类之间的相似性。 Fowlkes–Mallows指数值越高，聚类和基准分类越相似。可以使用以下公式计算:

   

   是真阳性的数量，    是假阳性的数量，并且    是假阴性的数量。    指数是精确度    和召回率    的几何平均值，因此也被称为G测度，而F测量是它们的调和平均数。^[40][41] 此外，精确度和召回率也被称为华莱士指数     和    。^[42] 召回率、精确度和G-测度的机会标准化版本对应于信息性、标记性和马修斯相关性，并与Kappa密切相关。^[43]

• 互信息是一种信息论度量，用于度量一个聚类和一个地面实况分类之间共享了多少信息，该分类可以检测两个聚类之间的非线性相似性。标准化的互信息是一系列的随机修正变量，对不同的聚类数有较小的偏差。^[30]
• 混淆矩阵

混淆矩阵可用于快速可视化分类(或聚类)算法的结果。它显示了集群与黄金标准集群的不同之处。

3.3 聚类趋势

测量聚类趋势是测量要聚类的数据中聚类存在的程度，并且可以在尝试聚类之前作为初始测试来执行。一种方法是将数据与随机数据进行比较。通常，随机数据不应该有聚类。

• 霍普金斯统计

霍普金斯统计有多种公式。^[44] 一个典型的例子如下。^[45] 在     维度空间内，设    为集合     数据点。考虑随机抽样(不替换)带有成员    的     数据点。也生成一个关于    均匀随机分布的数据点集合     。现在定义两个距离度量，     作为从    到它最近邻的X之间的距离，    作为从    到它最近邻的X之间的距离，然后我们定义霍普金斯统计量为:

   

根据这一定义，统一随机数据的值应该接近0.5，而聚类数据的值应该接近1。

然而，仅包含单个高斯分布的数据也将得分接近1，因为该统计量度测量偏离均匀分布而非多模态，使得该统计在应用中基本上无用（因为真实数据从不是远程统一的）。

应用程序

3.4 生物学、计算生物学和生物信息学

植物和动物生态学

聚类分析用于描述和进行异质环境中生物群落(组合)的空间和时间比较。它也被用于植物系统学，以在物种、属或更高级别上产生人工系统发育或生物(个体)集群，这些生物共享许多属性。

转录组学

聚类是用于建立具有相关表达模式的基因组(也称为共表达基因)，如在HCS聚类算法中。通常，这些组包含功能相关的蛋白质，如特定途径的酶或共调控的基因。使用表达序列标签或DNA微阵列的高通量实验可以成为基因组注释的有力工具——基因组学的一个一般方面。

序列分析

序列聚类用于将同源序列分组到基因家族中。这在生物信息学和进化生物学中是一个非常重要的概念。通过基因复制看进化。

高通量基因分型平台

聚类算法用于自动分配基因型。

人类遗传聚类

遗传数据的相似性被用于聚类来推断群体结构。

3.5 医学

医学成像

在PET扫描中，聚类分析可用于区分三维图像中不同类型的组织，以达到许多不同的目的。       ^[46]  

抗菌活性分析

聚类分析可用于分析抗生素耐药性模式，根据抗菌化合物的作用机制对其进行分类，根据抗菌活性对抗生素进行分类。

IMRT分割

在基于MLC的放射治疗中，聚类可用于将注量图分成不同的区域，以转换成可交付的字段。

3.6 商业和营销

市场调查

当使用来自调查和测试面板的多元数据时，聚类分析被广泛用于市场研究。市场研究人员使用聚类分析将一般消费者群体划分为细分市场，更好地理解不同消费者群体/潜在消费者之间的关系，并用于市场细分、产品定位、新产品开发和选择测试市场。

购物项目分组

聚类可以用来将网上所有的购物项目组合成一组独特的产品。例如，易趣上的所有商品都可以归入独特的产品(易趣没有“SKU”的概念)。

3.7 万维网

社会网络分析

在社交网络的研究中，聚类可以用来识别大群体中的社区。

搜索结果分组

在对文件和网站进行智能分组的过程中，与像谷歌这样的普通搜索引擎相比，聚类可以用来创建一组更相关的搜索结果 ^{[来源请求]}。目前有许多基于网络的聚类工具，如Clusty。它也可以用来返回一组更全面的结果，在这种情况下，一个搜索词可以指完全不同的东西。该术语的每一个不同用法对应于一个唯一的结果集群，允许排序算法通过从每个集群中挑选最重要的结果来返回综合结果。       ^[47]  

滑动映射优化

Flickr的照片地图和其他地图站点使用聚类来减少地图上标记的数量。这使得速度更快，并减少了视觉混乱的数量。

3.8 计算机科学

软件进化

集群在软件演化中很有用，因为它通过改造分散的功能来帮助减少代码中的遗留属性。这是一种重组形式，因此是一种直接预防性维护的方式。

图象分割法

聚类可用于将数字图像分成不同的区域，用于边界检测或对象识别。       ^[48]  

进化算法

聚类可用于识别进化算法群体中的不同小生境，以便繁殖机会可以在进化物种或亚种之间更均匀地分布。

推荐系统

推荐系统旨在根据用户的喜好推荐新的项目。 他们有时使用聚类算法根据用户群中其他用户的偏好来预测用户的偏好。

马尔科夫蒙特卡洛方法

聚类通常用于定位和表征目标分布中的极值。

异常检测

异常/异常值通常是针对数据中的聚类结构定义的，无论是显式的还是隐式的。

自然语言处理

聚类可以用来解决词汇歧义。       ^[47]  

3.9 社会科学

犯罪分析

聚类分析可用于确定特定类型犯罪发生率较高的领域。通过确定在一段时间内发生类似犯罪的不同地区或“热点”，有可能更有效地管理执法资源。

教育数据挖掘

例如，聚类分析用于识别具有相似属性的学校或学生群体。

类型学

从民意调查数据来看，皮尤研究中心开展的项目使用聚类分析来辨别可能对政治和营销有用的观点、习惯和人口统计的类型。

3.10 其他

野外机器人学

聚类算法用于机器人态势感知，以跟踪目标并检测传感器数据中的异常值。       ^[49]  

数学化学

寻找结构相似性等。例如，3000种化合物聚集在90个拓扑指数的空间中。       ^[50]  

气候学

寻找天气状况或更喜欢的海平面气压大气模式。       ^[51]  

金融

聚类分析被用来把股票分成几个部门。^[52]

石油地质学

聚类分析用于重建缺失的井底岩心数据或缺失的测井曲线，以评估储层性质。

自然地理

不同样品位置化学性质的聚集。

3.11 专门类型的聚类分析

• 自动聚类算法
• 平衡聚类
• 聚类高维数据
• 概念聚类
• 共识聚类
• 约束聚类
• 社区检测
• 数据流聚类
• HCS聚类
• 序列聚类
• 光谱聚类

3.12 聚类分析中使用的技术

• 人工神经网络
• 最邻近搜索
• 邻里成分分析
• 潜在类别分析
• 亲和力传播

3.13 数据投影和预处理

• 降维
• 主成分分析
• 多维标度

3.14 其他的

• 聚类加权建模
• 维数灾难
• 确定数据集中的集群数量
• 平行座标
• 结构化数据分析