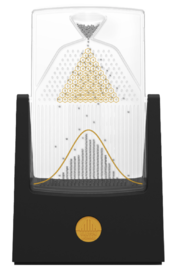
高尔顿钉板
编辑1 描述编辑
高尔顿板是一块竖直板,板上有交错排列的销钉。珠子从顶部落下,当装置水平放置时,珠子碰到销钉后弹向左边或右边,最终落入到底部的格子中,在格子中堆积的珠子高度最终将接近钟形曲线。如果将帕斯卡三角形叠加在格子上,就可以显示到达每个格子的不同路径的数量。[1]
查尔斯和雷·伊姆斯制作了这种装置的大型工作模型,在波士顿科学博物馆、纽约科学馆或亨利福特博物馆永久展出的《数学:数字的世界...又不止于此》展览中可以看到这些模型[2]。另一个大型模型版本展示在加利福尼亚州欧文市的指数基金顾问大厅里。[3]
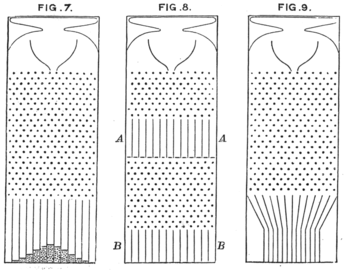
通过改变销钉的形状或将销钉朝向一个方向偏置,可以构造用于演示其他分布的豆机(甚至可以构造用于演示双峰分布的豆机)[4]。雅各布斯·卡普坦在研究和推广对数正态分布的统计数据时,建造了一台用于演示对数正态分布(在许多自然过程,特别是生物类的自然过程中,常见对数分布)的豆机,该豆机使用不同宽度的等腰三角形来“增加”珠子行进的距离,而不是将固定大小的行进步长累加,这种豆机有助于演示对数正态分布及其合理性[5]。(从1963年起,它被保存在格罗宁根大学中)[6]。埃克哈德·利珀斯设计了一种改进的对数正态豆机,它使用倾斜三角形,避免珠子的中间位置向左移动。[7]
2 珠子的分布编辑
如果一颗珠子在下落的过程中向右弹起k 次(在剩下的钉子上向左弹起),它将落在左边数第k个格子里。如果用n表示高尔顿板中销钉的行数,则珠子落入底部第k个格子的路径数量,可以通过如下的二项式系数获得 。如果在钉子上向右反弹的概率是 p (基于无偏估水平机,概率等于0.5),则珠子最终落入第k个格子的概率等于 。这是二项式分布的概率质量函数。行数对应于多次试验中二项式分布的大小,而在销钉向右反弹的概率 p 是二项式的 p。
根据中心极限定理(更具体地说,de Moivre-la place定理),假设行数和落珠数量都很大,则二项式分布近似于正态分布。改变行数将改变钟形曲线的标准偏差或宽度、或改变格子中的正态分布。
3 示例编辑
高尔顿板(7.5英寸乘4.5英寸)
被销钉反弹前后
豆机的复制品(遵循稍加修改的设计)
弗朗西斯·高尔顿爵士描绘的豆机
4 历史编辑
看似混乱的珠子被高尔顿板中的销钉反弹后形成钟形曲线,这一现象使弗朗西斯·高尔顿爵士着迷。他在《自然遗传》(1889)一书中雄辩地描述了这种关系:[8]
明显混乱中的秩序:我不知道还能有什么比误差频率定律所表现出来的宇宙秩序的奇妙形式更能打动想象力的了。如果希腊人早已知道这一定律的话,他们也许会将它人格化和神化。在最无序的混乱中,它平静地自我克制着。混乱状态越严重,它的影响力就越大。这是非理性的最高法则。每当手握大量混乱元素的样本,并按它们的数量级排列时,一种意想不到的、最美丽的规律性形式被证明一直存在着。
5 游戏编辑
根据利用销钉来改变小球或其他物体行进路线的想法,已经开发了多种游戏:
- 弹球
- 弹硬币
- 弹珠台
- 弹球
- 网格滴球
- 墙
参考文献
- [1]
^"The Galton Board". www.galtonboard.com (in 英语). Four Pines Publishing, Inc. Retrieved 2018-03-06..
- [2]
^"Henry Ford museum acquires Eames' Mathematica exhibit". Auction Central News. LiveAuctioneers. 20 March 2015. Retrieved 2018-03-06..
- [3]
^"IFA.tv - From Chaos to Order on the Galton Board -- A Random Walker". 23 December 2009. Retrieved 2018-03-06..
- [4]
^Brehmer et al 2018, "Mining gold from implicit models to improve likelihood-free inference": "Simulator Mining Example".
- [5]
^Kapteyn 1903, Skew frequency curves in biology and statistics v1; Kapteyn & van Uven 1916, Skew frequency curves in biology and statistics v2.
- [6]
^Aitchison & Brown 1963, The Lognormal Distribution, with Special Reference to its Uses in Economics.
- [7]
^Limpert et al 2001, "Log-normal Distributions across the Sciences: Keys and Clues".
- [8]
^Galton, Sir Francis (1894). Natural Inheritance. Macmillan..
暂无