The Wayback Machine - https://web.archive.org/web/20221025162719/https://baike.sogou.com/kexue/d10640.htm

光子晶体

编辑
这只手镯中的蛋白石含有天然的周期性微结构，使其表现出彩虹的颜色。这种蛋白石本质上是一种天然光子晶体。

光子晶体是一种可以调控光子传播的周期性的光学纳米结构，其对于光子的调控类似于离子晶格对电子运动的调控。光子晶体在自然界中表现为结构生色和动物皮毛反射颜色，在很多方面有广阔的应用前景。

1887年，英国物理学家瑞利勋爵（Lord Rayleigh）对多层周期性介电叠层进行了实验，实验结果表明这种结构具有一维光子带隙。自从1987年伊莱·亚布洛诺维奇（Eli Yablonovitch）和萨杰夫·约翰（Sajeev John）对多维周期性光学结构（今称光子晶体）进行了研究以后，学术界对于光子晶体的研究兴趣越来越大。

光子晶体可以制成一维、二维或三维的。一维光子晶体可以由沉积或堆叠在一起的介质层组成。二维的光子晶体可以通过在合适的衬底上钻孔或者光刻来制造。三维光子晶体的制造方法包括多角度钻孔、二维光子晶体层堆叠、激光直写、或者溶解基质中自组装的球体。

原则上，光子晶体可以应用在任何需要调控光场的地方。现有的一维光子晶体应用包括带有透镜涂层的薄膜光学器件。二维光子晶体光纤可用于制造非线性光学器件和特殊波段的光波导。三维光子晶体有望用于光学计算机。三维光子晶体可以作为电子设备的电源，制作更高效的光伏电池，从而减少电子器件对于能源的需求[1]。

1 介绍编辑

光子晶体由周期性电介质、金属电介质甚至超导体微结构或纳米结构组成，它调控电磁波传播的方式，就像半导体晶体中的周期电势通过电子能带来调控电子运动一样。光子晶体包含周期性重复的高介电常数和低介电常数的区域。光子 (表现为波)能不能通过这个光子晶体结构取决于波长。传播的波长称为模式，允许的模式组形成光子的导带，不允许的波段称为光子禁带（也称带隙）。这样的性质产生了独特的光学现象，例如自发辐射抑制、高反射全向反射镜和低损耗波导。光子晶体的带隙可以直观理解为由晶体中传播的光在高介电常数区域和低介电常数区域的界面处的多次反射的相消干涉产生，类似于固体中电子的带隙。

光子晶体结构的周期必须是被衍射电磁波波长的一半左右。对于可见光波段工作的光子晶体来说，大约350纳米(蓝色)到大约650纳米(红色)，平均折射率不同的话，周期可能会更小。因此，高介电常数和低介电常数的重复区域必须以这种尺度来制造，这非常的困难。

2 历史编辑

自1887年以来，光子晶体一直以各种形式被研究，但直到100多年后——在伊莱·亚布洛诺维奇（Eli Yablonovitch）和萨杰夫·约翰（Sajeev John）于1987年发表了两篇关于光子晶体的里程碑式论文之后——人们才开始使用光子晶体这个概念[2][2]。美国物理学会将光子晶体确定为物理学里程碑式的发展成果，并将光子晶体的早期发展历史以故事的形式很好地记录下来[3]。

在1987年之前，周期性多层介质叠层形式的一维光子晶体(例如布拉格镜)已经被广泛研究[4]。瑞利勋爵（Lord Rayleigh）在1887年开始的研究中证明了一维光子晶体具有一维光子带隙，即一个大反射率的光谱范围，这一波段今天被人们称为光子禁带。如今，这种结构被用于各种领域——从提高发光二极管发光效率的反射涂层，到特定激光腔中的高反射镜。 弗拉基米尔·比科夫（Vladimir P. Bykov）对一维光子晶体的光学结构进行了详细的理论研究[5]，首次研究了光子带隙对嵌入光子结构中的原子和分子自发辐射的影响。比科夫还预测了如果使用二维或三维周期性光学结构光子带隙对嵌入光子结构中的原子和分子自发辐射的影响[6]。之后的1979年Ohtaka讨论了三维光子晶体的概念[7]，他还开发了一种计算光子能带结构的方法。然而，这些方法一直到亚布洛诺维奇（Eli Yablonovitch）和约翰（Sajeev John）在1987年发表了两篇里程碑式的论文之后才开始起步。这两篇论文都涉及了高维周期光学结构，即光子晶体。亚布洛诺维奇（Yablonovitch）的主要目标是通过控制嵌入光子晶体的材料的自发辐射来调控光子态密度。约翰（Sajeev John）的想法是利用光子晶体来调控光子的局域化和传播。

1987年以后，关于光子晶体的研究论文开始呈指数级增长。然而，由于在光学尺度上制造这些结构的困难重重，早期的研究要么是理论上的，要么是在微波范围内，因为在微波频段光子晶体可以在更容易实现的厘米尺度上制造。(这是由于电磁场的尺度不变性。本质上，电磁场作为麦克斯韦方程的解，没有自然长度尺度——所以微波频率下厘米量级的解与光学频率下纳米量级的解性质相同)。

到1991年，亚布洛诺维奇（Yablonovitch）实现了微波频段中的首个拥有三维光子带隙的光子晶体[8]。亚布罗诺维奇（Yablonovitch）制造的结构是在透明材料上钻一系列孔，每一层的孔叠加起来形成一个反金刚石结构——今天这种结构被称为Yablonovite结构。

1996年，托马斯·克劳斯（Thomas Krauss）开创了利用半导体工业的方法在半导体材料中制造光子晶体的方法[9]。实现了光频段中的二维光子晶体。

今天，这种技术使用的是 “蚀刻”到半导体板上的二维光子晶体平板。通过全内反射将光限制在二维平板内，可以调控平板中的光子色散关系等光子晶体效应。世界各地的研究人员正在努力将光子晶体平板应用到在集成计算机芯片中，以优化芯片内和芯片间光学通信时的信息处理问题。

这种技术尚未成熟到商业应用，但是二维光子晶体已经在光子晶体光纤[10] (也称多孔光纤，因为这种结构中有很多孔洞)上实现商业化应用了。光子晶体最初于1998年开发，比(普通)光纤具有更好的性能。

三维光子晶体的研究进展比二维光子晶体更慢，这是因为三维光子晶体的制造更加困难[10]。三维光子晶体制造本身没有可供借鉴的半导体工业技术。然而，研究人员已经尝试改进了一些相同的技术，得到了一些成功的例子，例如在平面多层结构中制造的“木桩”结构。另一项研究试图依靠自组装构建三维光子结构——本质上是让电介质纳米球的混合物从溶液中沉降成具有光子带隙的三维周期性结构。伊夫研究所（Ioffe Institute）的瓦西里·阿斯特赖托夫（Vasily Astratov）研究小组在1995年认识到，天然的和人工合成的蛋白石是具有不完整带隙的光子晶体[11]。2000年，加拿大多伦多大学和西班牙马德里材料科学研究所(ICMM-CSIC)的研究人员首次实现了一种具有完整光子带隙的“反蛋白石”结构。 不断发展的仿生学领域——即研究自然结构以更好地理解和在设计中使用它们——也在帮助光子晶体领域的研究者[12][13]。例如，在2006年，研究人员在巴西甲虫的鳞片上发现了一种天然光子晶体 [14]。相似地，2012年研究人员不仅在象鼻虫中发现了钻石晶体结构[15][16]，还在蝴蝶中发现了螺旋形晶体结构[17]。

3 制造方法编辑

光子晶体的制造方法取决于光子带隙存在的维数。

  • '''一维、二维和三维光子晶体的可能结构示例'''

  • 一维、二维和三维光子晶体(从左到右)结构的比较。

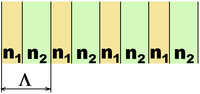
  • 一维光子晶体结构示意图，由高介电常数材料和低介电常数材料的交替层制成。每层的厚度通常为波长的四分之一。

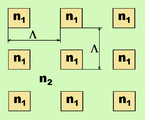
  • 正方形阵列的二维光子晶体结构。

  • 由圆孔构成的二维光子晶体示意图。

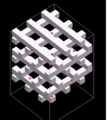
  • 木桩结构的三维光子晶体。这些结构对于所有偏振方向都具有三维带隙。

3.1 一维光子晶体

在一维光子晶体中，不同介电常数的层可以沉积或粘附在一起从而在单个方向上形成带隙。布拉格光栅就是这种光子晶体的一个例子。一维光子晶体可以是各向同性的，也可以是各向异性的，后者可以用作光学开关[18]。

一维光子晶体可以由无数超材料层和真空层交替平行排列的结构构成[19]。这种光子晶体可以对电磁TE波和TM波产生下相同的光子晶体结构。

最近，研究人员制作了一种基于石墨烯的布拉格光栅(一维光子晶体)，并证明了这种周期性结构在以633纳米氦氖激光器为光源时可以激发产生表面电磁波[20]。此外，研究人员还提出了一种新型的一维石墨烯介质光子晶体。这种结构可用作远红外滤波器，同时还可以产生低损耗表面等离子体激元，应用于波导和传感[21]。

3.2 二维光子晶体

在二维情况下，可以通过在特殊衬底上钻孔来制造光子晶体。衬底材料要可以传播带隙对应波长范围的电磁波。在这方面，三角形和正方形的孔格已经被成功地用于制造光子晶体。

多孔光纤或光子晶体光纤可以通过在六方晶格中采用圆柱形玻璃棒然后加热和拉伸而制成。玻璃棒之间的三角形气隙可以看做是这种结构中调控光学模式的孔格。

3.3 三维光子晶体

下列几种结构类型已经实现:[22]

  • 钻石晶格中的球体
  • Yablonovite结构
  • 木桩结构——“木桩”用激光光刻的方法反复蚀刻、填充并覆盖上一层新材料。随着该过程的重复，蚀刻在每一层中的通道与下一层相垂直，并且平行于下面两层的通道并与其相位相反。重复该过程，直到结构达到所需厚度。然后使用特定的溶剂溶解填充材料同时保留沉积材料。通常在该结构中很难引入缺陷。
  • 反蛋白石或反胶体晶体-球体(如聚苯乙烯或二氧化硅)可以沉积到悬浮在溶剂中的立方密堆积晶格中，然后加入硬化剂使溶剂占据的体积变成透明固体，接着用酸（如盐酸）溶解球体。由此产生的胶体含有超过75万个聚合物纳米棒。这些胶体既可以是球形的[23] 也可以是非球形的[23][24][25]。聚焦在这种分束器上的光会根据其偏振态被反射或者透射[26][27]。

A photonic crystal fiber
光子晶体光纤。美国NRL机构生产的光子晶体光纤的扫描电镜图像。光纤中心(左)的实心直径为5米， 而孔(右)的直径为4米。http://www.nrl.navy.mil/techtransfer/fs.php?fs_id=97

二维自组装PMMA光子晶体的扫描电镜图像

4 制造挑战编辑

高维光子晶体制造面临两大挑战:

  • 确保有足够高加工精度，以防止制造缺陷导致电磁散射，从而降低光子晶体的性能
  • 设计可以大规模量产的光子晶体的制造方法

二维周期性光子晶体的一种有前景的制造方法是利用光子晶体纤维，例如多孔光纤。为通信光纤开发的光纤拉制技术满足这两个要求，这种光子晶体光纤可以在市场上买到。开发二维光子晶体的另一种有前景的方法是所谓的光子晶体平板。这些结构使用半导体行业的刻蚀技术对一块平板材料(如硅)进行加工。这种芯片有潜力能够在单个芯片上同时实现光子处理和电子处理。

对于三维光子晶体的制造，用于集成电路的光刻和蚀刻技术等已经被广泛采用[28]。其中一些技术已经商业化。为了避免纳米技术制造方法的复杂机制，研究人员提出了一些替代方法比如以自组装结构的形式从胶体晶体中生长光子晶体。

现在人们可以通过使用剪切组装技术将200-300纳米胶体聚合物球堆叠成面心立方晶格（fcc）完美薄膜实现三维光子晶体薄膜和纤维的大规模生产。因为颗粒具有较软的透明橡胶涂层，所以其制成的薄膜可以拉伸和模塑，从而可以实现光子带隙的调节和显著的结构色彩效果。

5 计算光子带结构编辑

光子带隙(PBG)本质上是光子带隙（PBG）系统色散图中空气线和介质线之间的间隙。为了设计光子晶体系统，必须使用以下方法计算建模来设计带隙的位置和大小:

光子晶体结构中散射力和散射场的视频模拟[1]

  • 平面波展开法
  • 有限元法
  • 时域有限差分法
  • n阶谱方法[29][30]
  • KKR方法
  • 布洛赫波–矩量法（MoM）
  • 计算能带结构[31]

本质上，这些方法可以对波矢量给出的每个传播方向求出对应的光子晶体的频率(本征模式)，反之也可以通过给定光子晶体的频率求出对应波矢的传播方向。波段结构中的不同曲线对应于不同阶数n的能带。关于光子能带结构的介绍，见乔安诺普洛斯（Joannopoulos）[32]。

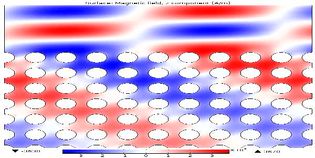
一维光子晶体的能带结构，用平面波展开方法利用101个平面波计算布拉格反射器(DBR)，其d/a=0.8，介电对比度为12.250。

平面波展开法用于通过麦克斯韦方程的本征公式计算能带结构，从而求解每个传播方向波矢的本征频率。它直接求解色散图。电场强度值也可以使用这一问题的特征向量在对应的空间域上计算。右边所示的图像对应于一维分布式布拉格反射器(DBR)的能带结构，在这种结构中空气层与相对介电常数为12.25的介电材料交错分布，并且在第一不可约布里渊区上使用101个平面波算出对应的晶格周期与空气层厚度之比(d/a)为0.8。

为了加速频带结构的计算，可以使用约化布洛赫模式展开法(RBME)。[33] RBME方法适用于上述任何一种主要展开方法的曲线“顶部”。对于大型单元结构模型，RBME方法可以将计算能带结构的时间最多减少两个数量级。

6 应用编辑

光子晶体是控制和操纵光流的热门光学材料。一维光子晶体已经以薄膜光学的形式广泛应用在从透镜和反射镜上的低反射涂层、高反射涂层到变色涂料和油墨的许多方面。基础研究和应用研究对高维光子晶体都有很大的兴趣，二维光子晶体也开始获得商业应用。

二维周期性光子晶体的第一批商业化产品，光子晶体光纤，使用微结构来束缚与传统光纤截然不同的特性的光，可以用于制造非线性光学器件和特殊波段的光波导。三维光子晶体商业化的道路还有很长的路要走，但是如果其制造工艺的主要困难（比如晶体结构有序度）得到突破的话，三维光子晶体可以用于制造光子计算机中的非线性光学晶体管。

参考文献

  • [1]

    ^Hwang, Dae-Kue; Lee, Byunghong; Kim, Dae-Hwan (2013). "Efficiency enhancement in solid dye-sensitized solar cell by three-dimensional photonic crystal". RSC Advances. 3 (9): 3017–23. doi:10.1039/C2RA22746K..

  • [2]

    ^Yablonovitch, Eli (1987). "Inhibited Spontaneous Emission in Solid-State Physics and Electronics". Physical Review Letters. 58 (20): 2059–62. Bibcode:1987PhRvL..58.2059Y. doi:10.1103/PhysRevLett.58.2059. PMID 10034639..

  • [3]

    ^Lindley, David (2013-08-23). "Focus: Landmarks—The Birth of Photonic Crystals". Physics (in 英语). 6..

  • [4]

    ^Rayleigh, Lord (2009). "XXVI. On the remarkable phenomenon of crystalline reflexion described by Prof. Stokes". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (160): 256–65. doi:10.1080/14786448808628259..

  • [5]

    ^Bykov, V. P (1972). "Spontaneous Emission in a Periodic Structure". Soviet Journal of Experimental and Theoretical Physics. 35: 269. Bibcode:1972JETP...35..269B..

  • [6]

    ^Bykov, Vladimir P (1975). "Spontaneous emission from a medium with a band spectrum". Soviet Journal of Quantum Electronics. 4 (7): 861–871. Bibcode:1975QuEle...4..861B. doi:10.1070/QE1975v004n07ABEH009654..

  • [7]

    ^Ohtaka, K (1979). "Energy band of photons and low-energy photon diffraction". Physical Review B. 19 (10): 5057–67. Bibcode:1979PhRvB..19.5057O. doi:10.1103/PhysRevB.19.5057..

  • [8]

    ^Yablonovitch, E; Gmitter, T; Leung, K (1991). "Photonic band structure: The face-centered-cubic case employing nonspherical atoms". Physical Review Letters. 67 (17): 2295–2298. Bibcode:1991PhRvL..67.2295Y. doi:10.1103/PhysRevLett.67.2295. PMID 10044390..

  • [9]

    ^, Bibcode:1996Natur.383..699K, doi:10.1038/383699a0 Missing or empty |title= (help).

  • [10]

    ^Jennifer Ouellette (2002), "Seeing the Future in Photonic Crystals" (PDF), The Industrial Physicist, 7 (6): 14–17, archived from the original (PDF) on August 12, 2011.

  • [11]

    ^Astratov, V. N; Bogomolov, V. N; Kaplyanskii, A. A; Prokofiev, A. V; Samoilovich, L. A; Samoilovich, S. M; Vlasov, Yu. A (1995). "Optical spectroscopy of opal matrices with CdS embedded in its pores: Quantum confinement and photonic band gap effects". Il Nuovo Cimento D. 17 (11–12): 1349–54. Bibcode:1995NCimD..17.1349A. doi:10.1007/bf02457208..

  • [12]

    ^Kolle, Mathias (2011), "Photonic Structures Inspired by Nature", Photonic Structures Inspired by Nature: (1st ed.), Bibcode:2011psin.book.....K, doi:10.1007/978-3-642-15169-9, ISBN 978-3-642-15168-2[页码请求].

  • [13]

    ^McPhedran, Ross C; Parker, Andrew R (2015). "Biomimetics: Lessons on optics from nature's school". Physics Today. 68 (6): 32. Bibcode:2015PhT....68f..32M. doi:10.1063/PT.3.2816..

  • [14]

    ^Galusha, Jeremy W; Richey, Lauren R; Gardner, John S; Cha, Jennifer N; Bartl, Michael H (2008). "Discovery of a diamond-based photonic crystal structure in beetle scales". Physical Review E. 77 (5): 050904. Bibcode:2008PhRvE..77e0904G. doi:10.1103/PhysRevE.77.050904. PMID 18643018..

  • [15]

    ^Wilts, B. D; Michielsen, K; Kuipers, J; De Raedt, H; Stavenga, D. G (2012). "Brilliant camouflage: Photonic crystals in the diamond weevil, Entimus imperialis". Proceedings of the Royal Society B: Biological Sciences. 279 (1738): 2524–30. doi:10.1098/rspb.2011.2651. PMC 3350696. PMID 22378806..

  • [16]

    ^Wilts, B. D; Michielsen, K; De Raedt, H; Stavenga, D. G (2011). "Hemispherical Brillouin zone imaging of a diamond-type biological photonic crystal". Journal of the Royal Society Interface. 9 (72): 1609–14. doi:10.1098/rsif.2011.0730. PMC 3367810. PMID 22188768..

  • [17]

    ^Wilts, B. D; Michielsen, K; De Raedt, H; Stavenga, D. G (2011). "Iridescence and spectral filtering of the gyroid-type photonic crystals in Parides sesostris wing scales". Interface Focus. 2 (5): 681–7. doi:10.1098/rsfs.2011.0082. PMC 3438581. PMID 24098853..

  • [18]

    ^Cao, Y; Schenk, J. O; Fiddy, M. A (2008). "Third Order Nonlinear Effect Near a Degenerate Band Edge". Optics and Photonics Letters. 1 (1): 1–7. doi:10.1142/S1793528808000033..

  • [19]

    ^Pravdin, K. V.; Popov, I. Yu. (2014). "Photonic crystal with negative index material layers" (PDF). Nanosystems: Physics, Chemistry, Mathematics. 5 (5): 626–643..

  • [20]

    ^Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "Excitation of surface electromagnetic waves in a graphene-based Bragg grating". Scientific Reports. 2: 737. Bibcode:2012NatSR...2E.737S. doi:10.1038/srep00737. PMC 3471096. PMID 23071901..

  • [21]

    ^Hajian, H; Soltani-Vala, A; Kalafi, M (2013). "Characteristics of band structure and surface plasmons supported by a one-dimensional graphene-dielectric photonic crystal". Optics Communications. 292: 149–57. Bibcode:2013OptCo.292..149H. doi:10.1016/j.optcom.2012.12.002..

  • [22]

    ^https://web.archive.org/web/20221025162719/http://ab-initio.mit.edu/book/photonic-crystals-book.pdf[full citation needed].

  • [23]

    ^Blanco, Alvaro; Chomski, Emmanuel; Grabtchak, Serguei; Ibisate, Marta; John, Sajeev; Leonard, Stephen W; Lopez, Cefe; Meseguer, Francisco; Miguez, Hernan; Mondia, Jessica P; Ozin, Geoffrey A; Toader, Ovidiu; Van Driel, Henry M (2000). "Large-scale synthesis of a silicon photonic crystal with a complete three-dimensional bandgap near 1.5 micrometres". Nature. 405 (6785): 437–40. Bibcode:2000Natur.405..437B. doi:10.1038/35013024. PMID 10839534..

  • [24]

    ^Hosein, Ian D; Lee, Stephanie H; Liddell, Chekesha M (2010). "Dimer-Based Three-Dimensional Photonic Crystals". Advanced Functional Materials. 20 (18): 3085–91. doi:10.1002/adfm.201000134..

  • [25]

    ^Hosein, Ian D; John, Bettina S; Lee, Stephanie H; Escobedo, Fernando A; Liddell, Chekesha M (2009). "Rotator and crystalline films viaself-assembly of short-bond-length colloidal dimers". J. Mater. Chem. 19 (3): 344–9. doi:10.1039/B818613H..

  • [26]

    ^"Optical computing gets a lift on butterfly wings". www.gizmag.com..

  • [27]

    ^Turner, Mark D; Saba, Matthias; Zhang, Qiming; Cumming, Benjamin P; Schröder-Turk, Gerd E; Gu, Min (2013). "Miniature chiral beamsplitter based on gyroid photonic crystals". Nature Photonics. 7 (10): 801. Bibcode:2013NaPho...7..801T. doi:10.1038/nphoton.2013.233..

  • [28]

    ^Review: S. Johnson (MIT) Lecture 3: Fabrication technologies for 3d photonic crystals, a survey.

  • [29]

    ^Ordejón, Pablo (1998). "Order-N tight-binding methods for electronic-structure and molecular dynamics". Computational Materials Science. 12 (3): 157–91. doi:10.1016/S0927-0256(98)00027-5..

  • [30]

    ^Richard M Martin, Linear Scaling 'Order-N' Methods in Electronic Structure Theory.

  • [31]

    ^"EM21 - EM Lab". emlab.utep.edu..

  • [32]

    ^John D Joannopoulos; Johnson SG; Winn JN; Meade RD (2008), "Photonic Crystals: Molding the Flow of Light", Photonic Crystals: Molding the Flow of Light (2nd ed.), Bibcode:2008pcmf.book.....J, ISBN 978-0-691-12456-8[页码请求].

  • [33]

    ^Hussein, M. I (2825). "Reduced Bloch mode expansion for periodic media band structure calculations". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 465 (2109): 2825–48. arXiv:0807.2612. Bibcode:2009RSPSA.465.2825H. doi:10.1098/rspa.2008.0471. JSTOR 30243411. Check date values in: |year= (help).

阅读 3244
版本记录

  • 暂无