The Wayback Machine - https://web.archive.org/web/20221028211502/https://baike.sogou.com/kexue/d10332.htm

卡诺图

编辑
卡诺图的一个例子。 该图像实际上显示了两个卡诺图：对于函数ƒ，使用 minterms （彩色矩形）并使用maxterms (灰色矩形）进行补充。 在图像中，E（）表示一个minterms的总和，在文章中表示为 \sum {m_i}.

卡诺图（Karnaugh map）是逻辑函数的一种图形表示，由莫里斯·卡诺（Maurice Karnaugh）发明。一个逻辑函数的卡诺图就是把该函数最小项表达式中的各最小项相应地填入一个方格图内，方格图称为卡诺图。

卡诺图的构造特点使卡诺图具有一个重要性质：可以从图形上直观地找出相邻最小项，两个相邻最小项可以合并为一个与项并消去一个变量。

卡诺图利用了人类的模式识别能力，减少了大量计算的需要。 它还允许快速识别和消除潜在的 竞态条件.

所需的布尔结果从 真值表 在二维网格上，在卡诺图中，网格是按顺序排列的 格雷码,[1] 并且每个单元位置代表输入条件的一种组合，而每个单元值代表相应的输出值。识别出1或0的最佳组，它们代表 语言的语音典型 原始真值表中的逻辑。[2] 这些术语可以用来编写表示所需逻辑的最简布尔表达式。

卡诺图被用来简化现实世界的逻辑要求，以便它们可以用最少数量的物理逻辑门来实现。一个积和表达式 总是可以使用 与门连接或门，和一个 和积表达式 导致或门连接与门。[3] 卡诺图也可以用来简化软件设计中的逻辑表达式。布尔条件，例如在 条件语句，会变得非常复杂，这使得代码难以读取和维护。一旦最小化，规范的乘积和表达式以及乘积和表达式可以直接使用“与”和“或”逻辑运算符来实现。[4] 至少从中世纪开始，就有了将简单逻辑表达式最小化的图解和机械方法。在20世纪50年代早期，人们开始开发更系统的方法来最小化复杂的表达式，但是直到20世纪80年代中后期，卡诺图才是实践中最常用的方法。[5]

1 例子编辑

卡诺图用于简化布尔代数功能。例如，考虑下面描述的布尔函数 真值表。

Truth table of a function
  A B C D      
0 0 0 0 0 0
1 0 0 0 1 0
2 0 0 1 0 0
3 0 0 1 1 0
4 0 1 0 0 0
5 0 1 0 1 0
6 0 1 1 0 1
7 0 1 1 1 0
8 1 0 0 0 1
9 1 0 0 1 1
10 1 0 1 0 1
11 1 0 1 1 1
12 1 1 0 0 1
13 1 1 0 1 1
14 1 1 1 0 1
15 1 1 1 1 0

下面是使用布尔变量描述非简化布尔代数中相同函数的两种不同符号A, B, C, D和它们的倒置。

  •     这里     是小项要映射的行(即真值表中输出为1的行)。
  •     这里     是maxterm要映射的(即真值表中输出为0的行)。

1.1 卡诺图

环形和平面上的K-map。点表示的珊格是相连的。

K-map创建。该图显示输入ABCD（真值表中最左边的值）的十进制表示，而不是输出值（真值表中最右边的值），因此它不是卡诺图。

在三个维度上，可以将矩形弯曲成圆环。

在上例中，四个输入变量可以以16种不同的方式组合，因此真值表有16行，卡诺图有16个位置。卡诺图因此被排列成4 × 4格网。

行和列索引(显示在卡诺图的顶部和左侧下方)按顺序排列格雷码而不是二进制数字顺序。格雷码确保每对相邻单元格之间只有一个变量发生变化。完整卡诺图的每个单元格都包含一个二进制数字，代表该输入组合的函数输出。

卡诺图构建完成后，它被用来从真值表中寻找一种最简单的可能形式—— 语言的语音典型。卡诺图中相邻的1代表简化表达式的机会。最终表达式的最小项(简称“最小项”)是通过在图中环绕1的组找到的。最小项组必须是矩形的，并且面积必须是2的幂(即1， 2、 4、 8…)。Minterm矩形应该尽可能大，不包含任何0。为了使每个组更大，组可以重叠。以下示例中的最佳分组由绿色、红色和蓝色线标记，红色和绿色组重叠。红色组是2 × 2平方，绿色组是4 × 1个矩形，重叠区域用棕色表示。

单元格通常用速记来表示，它描述了单元格所覆盖的输入的逻辑值。例如， AD 意味着一个覆盖2x2区域的单元A 和 D为真，即上图中编号为13、9、15、11的单元格。另一方面， AD 意味着那些 A是真的D 是假的(也就是说， D 是真的)。

网格是环形连接，这意味着矩形组可以跨越边缘(见图)。最右边的单元格实际上与最左边的单元格“相邻”，即相应的输入值仅相差一位；同样，最上层和最底层的也是如此。因此， AD 可以是一个有效的术语——它在顶部包括单元格12和8，在底部包括单元格10和14——如此 B, D，包括四个角。

1.2 解决办法

此图显示两个K-maps. 函数f（A，B，C，D）的K-map显示为对应于minterms的彩色矩形。 棕色区域是红色2×2正方形和绿色4×1矩形的重叠区域。f相反项K-map显示为灰色矩形，其对应于maxterms。

一旦卡诺图被构造出来，相邻的1被矩形和正方形的盒子连接起来，代数最小项就可以通过检查每个盒子中的变量保持不变来找到。

对于红色分组:

  • A 是相同的，并且在整个框中等于1，因此它应该包含在red minterm的代数表示中。
  • B 不保持相同的状态(从1转换到0)，因此应排除在外。
  • C 不会改变。它总是0，所以应该包括它的补码NOT-C。因此， C 应该包括在内。
  • D 变化，所以它被排除在外。

因此布尔积和表达式中的第一个最小项是AC。

对于绿色分组， A 和 B 保持同样的状态，同时C 和 D 改变。 B是0，必须先求反，然后才能包含它。因此，第二个项是AB。请注意，绿色分组与红色分组重叠是可以接受的。

同样，蓝色分组给出了术语BCD。

每个分组的解决方案被组合在一起:电路的正常形式是   。

因此卡诺图引导了

  

通过仔细应用布尔代数的公理，但是这样做所需的时间随着术语的数量呈指数级增长。

1.3 相反项

相反项，通过将0分组，以同样的方式求解函数的反函数。

覆盖反方向的三个术语都显示为带有不同颜色边框的灰色框:

  • 棕色: A, B
  • 黄金: A, C
  • 蓝色: BCD

这产生了相反的结果:

  

通过使用 德摩根定律，the总和的乘积可以确定:

  

1.4 无关项

这个值 对于ABCD = 1111 被"无关项"取代。 这将完全删除绿色背景的项，并允许红色项更大。 它还允许蓝色相反项移动并变大。

卡诺图还允许真值表包括”的函数的简单最小化无关项“条件。“无关项”条件是输入的组合，设计者不在乎输出是什么。因此，“无关项”条件可以包含在任何矩形组中，也可以排除在任何矩形组之外，无论哪个矩形组更大。它们通常在地图上用破折号或x表示

右边的示例与上面的示例相同，但值为f(1，1，1，1)替换为“无关项”。这允许红色项一直向下扩展，从而完全删除绿色项。

这产生了新的最小方程:

  

请注意，第一个项只是 A，不是 AC。在这种情况下，无关项已经删除了一个项(绿色矩形)；简化另一个(红色的)；并删除了比赛危险(删除黄色项，如以下比赛危险部分所示)。

相反的情况简化如下:

  

2 竞争危害编辑

2.1 淘汰

卡诺图有助于检测和消除 竞态条件.使用卡诺图很容易发现竞争危险，因为在地图上任何一对相邻但不相交的区域之间移动时，都可能存在竞争状况。然而，由于灰色编码的性质， 邻近的 上面有一个特殊的定义——我们实际上是在一个圆环上运动，而不是在一个矩形上，围绕着顶部、底部和侧面。

  • 在这个例子中 超过，存在潜在的竞争条件 C 是1和 D 是0， A 是1，并且 B 从1变为0(从蓝色状态变为绿色状态)。在这种情况下，输出被定义为保持不变为1，但是因为这个转换没有被等式中的特定项覆盖，所以 小故障 (输出瞬间转变为0)存在。
  • 在同一个例子中，还有第二个潜在故障更难发现:什么时候 D 是0和 A 和 B 都是1，C从1变为0(从蓝色状态变为红色状态)。在这种情况下，毛刺从地图的顶部绕到底部。

此图中存在竞争危险。

上图中添加了一致项以避免竞争危险。

故障是否会真正发生取决于实现的物理性质，我们是否需要担心它取决于应用程序。在钟控逻辑中，只要该逻辑及时确定所需值，以满足时序截止时间，就足够了。在我们的例子中，我们不考虑时钟逻辑。

在我们的案例中，一个附加项    将消除潜在的竞争危险，在绿色和蓝色输出状态或蓝色和红色输出状态之间架起桥梁:这在相邻图中显示为黄色区域(从右半部分的底部到顶部环绕)。

项是 多余的 就系统的静态逻辑而言，但这种冗余，或 共识条款，通常是确保无竞争动态性能所必需的。

同样，附加项    必须添加到反方向，以消除另一个潜在的竞争危险。应用德·摩根定律创造了另一个求和表达式的乘积 f，但是有了一个新的因素   。

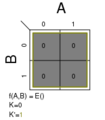
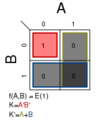
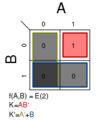
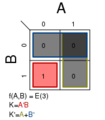
2.2 两变量图示例

以下是所有可能的2个变量，2 × 2的卡诺图。每一个都列出了作为函数的最小项    并且没有竞争危险(看见 )最小方程。minterm被定义为给出映射变量的最小表达式形式的表达式。可以形成所有可能的水平和垂直互连块。这些块的大小必须是2 (1，2，4，8，16，32，...)。这些表达式为要映射的二进制表达式创建最小逻辑变量表达式的最小逻辑映射。这里是所有有一个字段的块。

块可以在图表的底部、顶部、左侧或右侧连接。这甚至可以绕过图表的边缘，实现变量最小化。这是因为每个逻辑变量对应于每个垂直列和水平行。k-map的可视化可以被认为是圆柱形的。左侧和右侧边缘的字段相邻，顶部和底部相邻。四个变量的k-Maps映射必须描述为圆环或圆环形状。k-map的正方形的四个角是相邻的。5个变量和更多变量需要更复杂的映射。

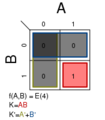
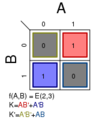
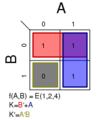
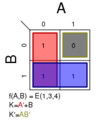
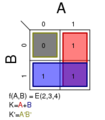
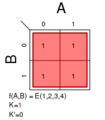
  • Σm(0); K = 0

  • Σm(1); K = A′B′

  • Σm(2); K = AB′

  • Σm(3); K = A′B

  • Σm(4); K = AB

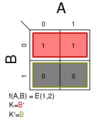
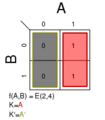
  • Σm(1,2); K = B′

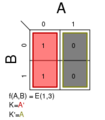
  • Σm(1,3); K = A′

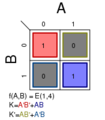
  • Σm(1,4); K = A′B′ + AB

  • Σm(2,3); K = AB′ + A′B

  • Σm(2,4); K = A

  • Σm(3,4); K = B

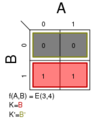
  • Σm(1,2,3); K = A' + B′

  • Σm(1,2,4); K = A + B′

  • Σm(1,3,4); K = A′ + B

  • Σm(2,3,4); K = A + B

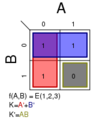
  • Σm(1,2,3,4); K = 1

3 其他图形方法编辑

可选的图形最小化方法包括:

  • 马夸德图 (1881)作者 Allan Marquand (1853-1924)[6][6]
  • 哈佛最小化图表 (1951)作者 Howard H. Aiken 和玛莎·怀特豪斯 哈佛计算实验室[6][7][7][8]
  • Veitch图表 (1952)作者 爱德华·韦奇 (1924-2013)[8][6]
  • 斯沃博达的图形辅助工具(1956年)和 三元映射 经过 antonin Svoboda (1907-1980)[8][9][10][11]
  • handler圆图 (又名 Händler'scher Kreisgraph, Kreisgraph nach Händler, Händler-Kreisgraph, Händler-Diagramm, Minimisierungsgraph[sic])(1958)作者 Wolfgang Hä ndler (1920-1998年)[12][13][14][10][15][16][17][18][19]
  • 图表法(1965年) Herbert Kortum [de] (1907-1979)[20][21][22][23][24][25][26]

参考文献

  • [1]

    ^Wakerly, John F. (1994). Digital Design: Principles & Practices. New Jersey, USA: Prentice Hall. pp. 222, 48–49. ISBN 0-13-211459-3. (NB. The two page sections taken together say that K-maps are labeled with Gray code. The first section says that they are labeled with a code that changes only one bit between entries and the second section says that such a code is called Gray code.).

  • [2]

    ^Belton, David (April 1998). "Karnaugh Maps – Rules of Simplification". Archived from the original on 2017-04-18. Retrieved 2009-05-30..

  • [3]

    ^Dodge, Nathan B. (September 2015). "Simplifying Logic Circuits with Karnaugh Maps" (PDF). The University of Texas at Dallas, Erik Jonsson School of Engineering and Computer Science. Archived (PDF) from the original on 2017-04-18. Retrieved 2017-04-18..

  • [4]

    ^Cook, Aaron. "Using Karnaugh Maps to Simplify Code". Quantum Rarity. Archived from the original on 2017-04-18. Retrieved 2012-10-07..

  • [5]

    ^Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1097. ISBN 1-57955-008-8..

  • [6]

    ^Brown, Frank Markham (2012) [2003, 1990]. Boolean Reasoning - The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-42785-0. [1].

  • [7]

    ^Karnaugh, Maurice (November 1953) [1953-04-23, 1953-03-17]. "The Map Method for Synthesis of Combinational Logic Circuits" (PDF). Transactions of the American Institute of Electrical Engineers part I. 72 (9): 593–599. doi:10.1109/TCE.1953.6371932. Paper 53-217. Archived (PDF) from the original on 2017-04-16. Retrieved 2017-04-16. (NB. Also contains a short review by Samuel H. Caldwell.).

  • [8]

    ^Curtis, H. Allen (1962). A new approach to the design of switching circuits. Bell Laboratories Series. Princeton, New Jersey, USA: D. van Nostrand Company, Inc..

  • [9]

    ^Svoboda, Antonín (1956). Graphical Mechanical Aids for the Synthesis of Relay Circuits. Nachrichtentechnische Fachberichte (NTF), Beihefte der Nachrichtentechnischen Zeitschrift (NTZ). Braunschweig, Germany: Vieweg-Verlag..

  • [10]

    ^Steinbuch, Karl W.; Weber, Wolfgang; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik - Band II - Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (in German). 2 (3 ed.). Berlin, Germany: Springer-Verlag. pp. 25, 62, 96, 122–123, 238. ISBN 3-540-06241-6. LCCN 73-80607.CS1 maint: Unrecognized language (link).

  • [11]

    ^Svoboda, Antonín; White, Donnamaie E. (2016) [1979-08-01]. Advanced Logical Circuit Design Techniques (PDF) (retyped electronic reissue ed.). Garland STPM Press (original issue) / WhitePubs (reissue). ISBN 978-0-8240-7014-4. Archived (PDF) from the original on 2017-04-14. Retrieved 2017-04-15. [2] [3].

  • [12]

    ^Händler, Wolfgang (1958). Ein Minimisierungsverfahren zur Synthese von Schaltkreisen (Minimisierungsgraphen) (Dissertation) (in German). Technische Hochschule Darmstadt. D 17.CS1 maint: Unrecognized language (link) [4] (NB. Although written by a German, the title contains an anglicism; the correct German term would be "Minimierung" instead of "Minimisierung".).

  • [13]

    ^Händler, Wolfgang (2013) [1961]. "Zum Gebrauch von Graphen in der Schaltkreis- und Schaltwerktheorie". In Peschl, Ernst Ferdinand; Unger, Heinz. Colloquium über Schaltkreis- und Schaltwerk-Theorie - Vortragsauszüge vom 26. bis 28. Oktober 1960 in Bonn - Band 3 von Internationale Schriftenreihe zur Numerischen Mathematik [International Series of Numerical Mathematics] (ISNM) (in German). 3. Institut für Angewandte Mathematik, Universität Saarbrücken, Rheinisch-Westfälisches Institut für Instrumentelle Mathematik: Springer Basel AG / Birkhäuser Verlag Basel. pp. 169–198. doi:10.1007/978-3-0348-5770-3. ISBN 978-3-0348-5771-0.CS1 maint: Unrecognized language (link) [5].

  • [14]

    ^Berger, Erich R.; Händler, Wolfgang (1967) [1962]. Steinbuch, Karl W.; Wagner, Siegfried W., eds. Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. pp. 64, 1034–1035, 1036, 1038. LCCN 67-21079. Title No. 1036. […] Übersichtlich ist die Darstellung nach Händler, die sämtliche Punkte, numeriert nach dem Gray-Code […], auf dem Umfeld eines Kreises anordnet. Sie erfordert allerdings sehr viel Platz. […] [Händler's illustration, where all points, numbered according to the Gray code, are arranged on the circumference of a circle, is easily comprehensible. It needs, however, a lot of space.]CS1 maint: Unrecognized language (link).

  • [15]

    ^Hotz, Günter (1974). Schaltkreistheorie [Switching circuit theory]. DeGruyter Lehrbuch (in German). Walter de Gruyter & Co. p. 117. ISBN 3-11-00-2050-5. […] Der Kreisgraph von Händler ist für das Auffinden von Primimplikanten gut brauchbar. Er hat den Nachteil, daß er schwierig zu zeichnen ist. Diesen Nachteil kann man allerdings durch die Verwendung von Schablonen verringern. […] [The circle graph by Händler is well suited to find prime implicants. A disadvantage is that it is difficult to draw. This can be remedied using stencils.]CS1 maint: Unrecognized language (link).

  • [16]

    ^"Informatik Sammlung Erlangen (ISER)" (in German). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Archived from the original on 2017-05-16. Retrieved 2017-04-12.CS1 maint: Unrecognized language (link) (NB. Shows a picture of a Kreisgraph by Händler.).

  • [17]

    ^"Informatik Sammlung Erlangen (ISER) - Impressum" (in German). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Archived from the original on 2012-02-26. Retrieved 2017-04-15.CS1 maint: Unrecognized language (link) (NB. Shows a picture of a Kreisgraph by Händler.).

  • [18]

    ^Zemanek, Heinz (2013) [1990]. "Geschichte der Schaltalgebra" [History of circuit switching algebra]. In Broy, Manfred. Informatik und Mathematik [Computer Sciences and Mathematics] (in German). Springer-Verlag. pp. 43–72. ISBN 9783642766770. Einen Weg besonderer Art, der damals zu wenig beachtet wurde, wies W. Händler in seiner Dissertation […] mit einem Kreisdiagramm. […]CS1 maint: Unrecognized language (link) [6] (NB. Collection of papers at a colloquium held at the Bayerische Akademie der Wissenschaften, 1989-06-12/14, in honor of Friedrich L. Bauer.).

  • [19]

    ^Bauer, Friedrich Ludwig; Wirsing, Martin (March 1991). Elementare Aussagenlogik (in German). Berlin / Heidelberg: Springer-Verlag. pp. 54–56, 71, 112–113, 138–139. ISBN 978-3-540-52974-3. […] handelt es sich um ein Händler-Diagramm […], mit den Würfelecken als Ecken eines 2m-gons. […] Abb. […] zeigt auch Gegenstücke für andere Dimensionen. Durch waagerechte Linien sind dabei Tupel verbunden, die sich nur in der ersten Komponente unterscheiden; durch senkrechte Linien solche, die sich nur in der zweiten Komponente unterscheiden; durch 45°-Linien und 135°-Linien solche, die sich nur in der dritten Komponente unterscheiden usw. Als Nachteil der Händler-Diagramme wird angeführt, daß sie viel Platz beanspruchen. […]CS1 maint: Unrecognized language (link).

  • [20]

    ^Kortum, Herbert (1965). "Minimierung von Kontaktschaltungen durch Kombination von Kürzungsverfahren und Graphenmethoden" [Minimization of contact circuits by combination of reduction procedures and graphical methods]. messen-steuern-regeln (msr) (in German). Verlag Technik [de]. 8 (12): 421–425. ISSN 0026-0347. CODEN MSRGAN.CS1 maint: Unrecognized language (link) [7].

  • [21]

    ^Kortum, Herbert (1966). "Konstruktion und Minimierung von Halbleiterschaltnetzwerken mittels Graphentransformation". messen-steuern-regeln (msr) (in German). Verlag Technik [de]. 9 (1): 9–12. ISSN 0026-0347. CODEN MSRGAN.CS1 maint: Unrecognized language (link).

  • [22]

    ^Kortum, Herbert (1966). "Weitere Bemerkungen zur Minimierung von Schaltnetzwerken mittels Graphenmethoden". messen-steuern-regeln (msr) (in German). Verlag Technik [de]. 9 (3): 96–102. ISSN 0026-0347. CODEN MSRGAN.CS1 maint: Unrecognized language (link).

  • [23]

    ^Kortum, Herbert (1966). "Weitere Bemerkungen zur Behandlung von Schaltnetzwerken mittels Graphen. Konstruktion von vermaschten Netzwerken (Brückenschaltungen)" [Further remarks on treatment of switching networks by means of graphs]. messen-steuern-regeln (msr) (in German). Verlag Technik [de]. 9 (5): 151–157. ISSN 0026-0347. CODEN MSRGAN.CS1 maint: Unrecognized language (link) Kortum, Herbert (1965). "Weitere Bemerkungen zur Behandlung von Schaltnetzwerken mittels Graphen" [Further remarks on treatment of switching networks by means of graphs]. Regelungstechnik (in German). 10. Internationales Wissenschaftliches Kolloquium, Ilmenau. Technische Hochschule. 10 (5): 33–39.CS1 maint: Unrecognized language (link).

  • [24]

    ^Kortum, Herbert (1967). "Über zweckmäßige Anpassung der Graphenstruktur diskreter Systeme an vorgegebene Aufgabenstellungen". messen-steuern-regeln (msr) (in German). Verlag Technik [de]. 10 (6): 208–211. ISSN 0026-0347. CODEN MSRGAN.CS1 maint: Unrecognized language (link).

  • [25]

    ^Kortum, Herbert (1966). "Zur Minimierung von Schaltsystemen" [Minimization of switching circuits]. Wissenschaftliche Zeitschrift der TU Ilmenau (in German). Jena: Technische Hochschule für Elektrotechnik Ilmenau / Forschungsstelle für Meßtechnik und Automatisierung der Deutschen Akademie der Wissenschaften. 12 (2): 181–186.CS1 maint: Unrecognized language (link).

  • [26]

    ^Tafel, Hans Jörg (1971). "4.3.5. Graphenmethode zur Vereinfachung von Schaltfunktionen". Written at RWTH, Aachen, Germany. Einführung in die digitale Datenverarbeitung [Introduction to digital information processing] (in German). Munich, Germany: Carl Hanser Verlag. pp. 98–105, 107–113. ISBN 3-446-10569-7.CS1 maint: Unrecognized language (link).

阅读 8398
版本记录

  • 暂无