The Wayback Machine - https://web.archive.org/web/20221028230610/https://baike.sogou.com/kexue/d10312.htm

AVT统计滤波算法

编辑

AVT统计滤波算法是一种提高从各种来源收集的原始数据质量的方法。它在存在带内噪声的情况下最有效。在这些情况下，AVT相比带通滤波器或任何基于变化的数字滤波，更擅长对数据进行滤波。

当信号/数据具有不同于噪声的频率，并且信号/数据通过噪声的频率辨别被分离/滤波时，传统滤波是有用的。鉴频滤波使用低通、高通和带通滤波来完成，该滤波是指用于这种配置的相对频率滤波标准目标。这些滤波器使用无源和有源组件搭建，有时使用基于快速傅立叶变换的软件算法来实现。

AVT滤波在软件中实现，其内部工作是基于对原始数据的统计分析。

当信号频率/（有用数据分布频率）与噪声频率/（噪声数据分布频率）一致时，就存在带内噪声。在这种情况下，鉴频滤波不起作用，因为噪声和有用信号是无法区分的，此时正是AVT发挥作用之处。为了在这种情况下实现滤波，有几种可用的方法/算法，下面将简要描述。

1 平均算法编辑

  1. 收集n个数据样本
  2. 计算收集数据的平均值
  3. 将结果作为实际数据呈现/记录

2 中值算法编辑

  1. 收集n个数据样本
  2. 按升序或降序对数据进行排序。请注意，顺序并不重要
  3. 选择恰好在n/2位置的数据，并将其作为代表数据样本的最终结果呈现/记录

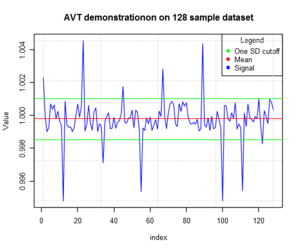
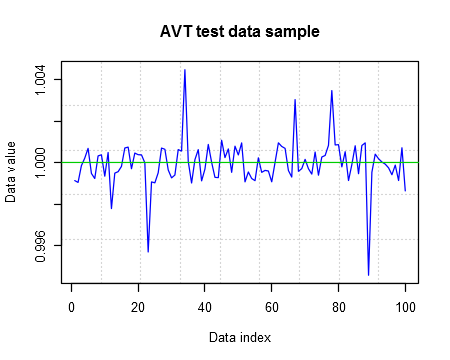
3 AVT算法编辑

AVT内部工作图

AVT算法代表安东尼·瓦尔丹变换及其实现，其实现如下。

  1. 收集n个数据样本
  2. 计算标准偏差和平均值
  3. 丢弃任何大于或小于平均一个标准偏差的数据
  4. 计算剩余数据的平均值
  5. 将结果显示/记录为代表数据样本的实际值

该算法基于振幅鉴别，可以很容易地消除任何与实际信号不同的噪声，否则在统计上不同于信号的1个标准偏差。请注意，这种类型的滤波可用于事先不知道实际环境噪声的情况。

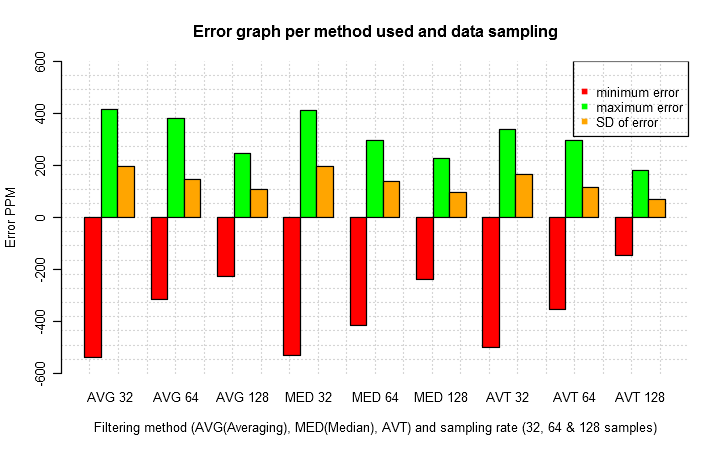
4 过滤算法比较编辑

使用信号值为1且噪声在0.1%和1%水平上增加的系统将简化算法性能的量化。R脚本程序[1] 用于创建添加到信号中的伪随机噪声，并使用几种算法分析滤波结果。详情请参考“用AVT算法降低带内噪声” [2] 文章。该图显示，当使用32、64和128个值的数据样本量时，与中值和平均算法相比，AVT算法提供了最佳结果。注意，此图是通过分析包含10000个值的随机数据数组创建的。下面用图形表示此数据的示例。

AVT algorithm comparison
AVT test data sample

5 AVT算法变体编辑

5.1 级联AVT

在某些情况下，通过级联几段AVT滤波可以获得更好的结果。这将产生奇异的常数值，可用于具有已知稳定特性的设备，如温度计、热敏电阻和其他慢作用传感器。

5.2 逆转AVT

  1. 收集n个数据样本
  2. 计算标准偏差和平均值
  3. 丢弃一个标准偏差平均带内的任何数据
  4. 计算剩余数据的平均值
  5. 将结果作为实际数据呈现/记录

这对于检测接近背景噪声水平的微小信号非常有用。

6 可能的应用和用途编辑

  • 用于行星探测，过滤开普勒（宇宙飞船）的原始数据
  • 从所有其他滤波方法（低通滤波器、高通滤波器、带通滤波器、数字滤波器）失效的声源中滤除噪声
  • 绘图前，对科学数据进行预处理，以便进行数据分析（平滑度），请参见绘图（图形）
  • 用于搜寻外星智能，用于探测/区分来自宇宙背景的外星信号

参考文献

  • [1]

    ^"The R Project for Statistical Computing". r-project.org. Retrieved 2015-01-10..

  • [2]

    ^"Reduce Inband Noise with the AVT Algorithm | Embedded content from Electronic Design". electronicdesign.com. Retrieved 2015-01-10..

阅读 42
版本记录

  • 暂无