HCS聚类算法

聚类分析的目标是基于元素之间的相似性将元素分组为不相交的子集或聚类，使得同一聚类中的元素彼此高度相似（同质性），而来自不同聚类的元素彼此相似性较低（分离性）。相似图是表示元素间相似性的模型之一，它反过来又有助于聚类的生成。为了通过相似性数据构建相似性图，将元素表示为顶点，并且当顶点之间的相似度的值高于某个阈值时，引出顶点对之间的边。

在相似性图中，给定数量的顶点存在的边越多，这样一组顶点彼此之间就越相似。换句话说，如果我们试图通过移除边来断开相似性图，那么在图断开之前我们需要移除的边越多，图中的顶点就越相似。最小割是一组边的最小集合，没有这些边，图将变得不相连。

HCS聚类算法找到所有具有n个顶点的子图，使得这些子图的最小割包含多于n/2条边，并将它们识别为聚类。这种子图被称为高度连通子图（HCS）。单个顶点不被认为是（一个独立的）簇，而是被分组到单例集合S中。

给定相似性图G（V，E），HCS聚类算法将检查它是否已经高度连接，如果是，返回G，否则使用G的最小割将G划分为两个子图H和H’，并递归地在H和H’上运行HCS聚类算法。

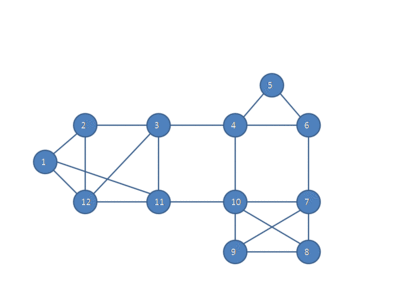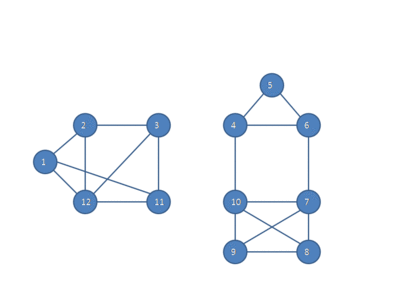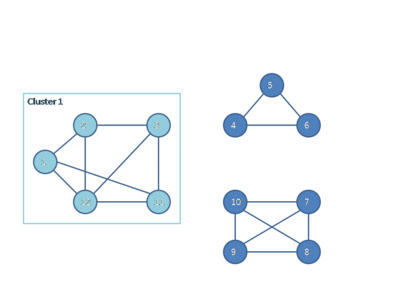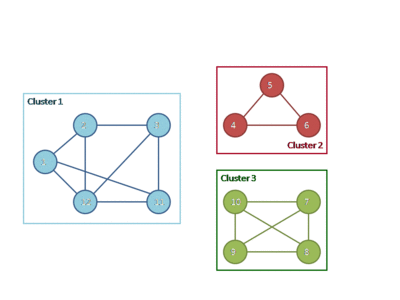
以下动画显示了HCS聚类算法如何将相似性图划分为三个聚类。

1  function HCS(G(V,E))   
2    if G is highly connected
3      then return (G)
4    else
5     (H1,H2,C) ← MINIMUMCUT(G)
6      HCS(H1)
7      HCS(H2)
8    end if
9  end

在图G上找到最小割的步骤是一个子程序，可以用不同的算法来解决这个问题。参见下文，了解使用随机化寻找最小切割的示例算法。

HCS聚类算法的运行时间以N×f（N，m）为界。f（n，m）是在有N个顶点和m条边的图中计算最小割的时间复杂度，N是找到的聚类数。在许多应用中N<<n（N远小于n）

HCS聚类算法产生的聚类具有多种性质，可以证明解的同质性和分离性。

定理1 每个高度连通的图的直径至多为2。

证明：我们知道最小割的边必须大于或等于图的最小度。如果图形G是高度连通的，那么最小割的边必须大于顶点数除以2。所以高度连通图G中的顶点的度数必须大于顶点的一半。因此，对于图G中的任意两个顶点，必须至少有一个公共邻节点，因为它们之间的距离是2。

定理2 （a）高度连通子图中的边数和顶点数的二次方成正比。（b）HCS算法每一次迭代所去除的边数最多是和顶点数成线性的。

证明：（对a）从定理1我们知道每个顶点必须有一半以上的顶点作为邻节点。因此，高度连接子图中的边总数必须至少为（n/2） * n * 1/2，其中我们将每个顶点的所有度数相加，然后除以2。

（对于b）每次迭代，HCS算法将一个包含n个顶点的图分成两个子图，因此这两个分量之间的边数最多为n/2。

定理1和2a为同质性提供了强有力的证明，因为就直径而言，唯一更好的可能性是聚类的每两个顶点由一条边连接，这既过于严格，也是NP难问题。

定理2b还表明了分离性，因为与最终聚类内的二次边数相比，HCS算法的每次迭代移除的边数在底层子图的大小上最多是线性的。

单例采用：初始聚类过程中作为单例留下的元素可以基于与聚类的相似性被聚类“采用”。如果（该顶点与）特定聚类的最大邻节点数量足够大，则可以将其添加到该聚类。

移除低度顶点：当输入图的顶点具有低度时，不值得运行该算法，因为计算量大且信息不丰富。或者，算法的一种改进方案可以是首先移除度数低于特定阈值的所有顶点。

• 基因表达分析^[2] ：合成寡核苷酸与排列有序的cDNA杂交过程中产生每个cDNA克隆体的指纹。在这些指纹上运行HCS算法可以识别对应于同一基因的克隆。

• 质子泵抑制剂网络结构发现^[3] 使用HCS聚类检测质子泵抑制剂中可能具有生物学意义并代表生物学过程的密集子网。
• "聚类算法综述."神经网络，IEEE Transactions ^[4]
• 点击聚类算法^[5] 是HCS算法在加权相似度图上的一种改版，其中权重被赋予为一种喜好的可能。
• 将生物网络划分为具有最大边缘覆盖的高连接集群^[6]

• R 语言文档