五个室拼图

上图：在平面上的失败尝试——没有穿过的墙用红叉表示下图：在圆环上的解——请注意，这条线有一段是沿着圆环的背面不可见的

戈尼斯堡七桥问题与五房间问题的对比。数字表示每个顶点的边数。边数为奇数的顶点用橙色表示。

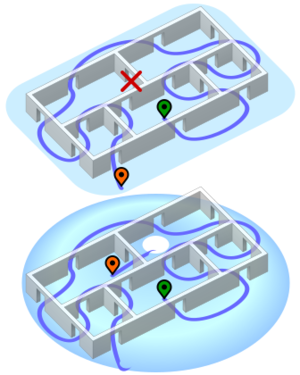
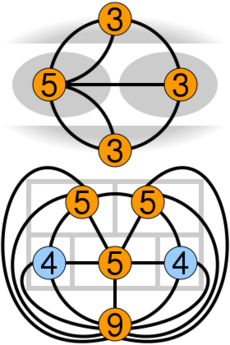
就像柯尼斯堡七桥问题一样，这个问题可以用图的形式来表示，每个房间对应一个顶点(包括房间的外部区域)，如果两个房间之间有一面公共墙，则两个顶点由一条边连接。因为有多对顶点有奇数条边，所以得到的多重图中不包含欧拉路径或欧拉回路，这意味着这个难题无法解决。

通过改变规则，一个相关的难题就可以解决了。例如，通过允许一次穿过一面以上的墙(即通过房间的一角)，或者通过在环面上(类似于甜甜圈)而不是平面上解决难题。

即使没有使用图论，也不难看出五房间问题没有解。首先，必须阐明规则。“房间”和其解的线都必须绘制在普通平面纸张的单面上。其解的线必须是连续的，但可以以任何方式急剧或平滑弯曲，甚至可以越过自身(但不能越过墙壁，因此这通常是被禁止的)。该问题解的线必须恰好穿过每面“墙”一次，其中“穿过”是指从完全被“墙”分隔的两个房间中的一个房间穿过到另一个房间，或者从一个房间穿过到矩形外的区域。这就排除了通过两堵“墙”相交的拐角画线来同时“跨越”两堵墙的可能性。它这也排除了通过将线画在墙面上或沿着墙面“穿过”墙壁但从墙壁的同一侧离开的可能性。有这里有16面“墙”，7个分隔房间分隔的房间和9个在图外的区域分隔的房间。

证明的方法是用反证法来证明的。也就是说，我们就假设存在一个解，并继续探寻解的一些属性。这些属性让我们陷入了一个不可能的境地，因此我们不得不断定我们错了——这个问题终究没有解的。^[3]

想象一下，每个“房间”里都有一个“观察者”。观察者在其进入他的房间的时候可以在他的房间里看到该问题解的线，但其他地方看不到。随着该问题解的线的绘制，他会看到它从一面墙进入他的房间，然后从另一面墙离开。他也可能看到解的线从他的房间开始和/或在他的房间结束。在图外的区域没有观察者，所以共有五个观察者。

首先，考虑一下在左下角和右下角房间的观察者。这些房间都有四面墙。如果该问题解的线从这两个房间中的一个开始，在其中的观察者会看到线穿过墙壁离开。然后它会通过另一面墙回到房间，再通过第三面墙离开。最后，它将通过第四面墙回到房间并结束。如果该问题解的线从其他地方开始，观察者将会看到该问题解的线以某种顺序穿过所有四面墙，进入和离开他的房间分别正好两次。这些都没有任何问题。

但是，请考虑其余三个房间中的观察者。这些房间都有五面墙。如果该问题解的线从这些房间中的一个开始，在其中的观察者将看到线离开(穿过一面墙)，再次进入和离开(另外两面墙)，并再次进入和离开(最后两面墙)。如果该问题解的线从其他地方开始，观察者将看到该问题解的线进入和离开(两堵墙)，第二次进入和离开(另外两堵墙)，最后通过第五堵墙进入并结束(所有五堵墙都已被穿过，因此该线不能再次离开房间)。因此，我们看到，对于有五面墙的房间，该问题解的线必须从这个房间内开始，或者必须在房间内结束。没有其他可能了。在我们的论点中，我们没有说该问题解的线到底穿过了哪些墙，穿过它们的顺序，或者当它在一个特定的房间之外时去了哪里。因此，这些论点适用于所有遵守规则的解。同样，对于有五面墙的房间，该问题解的线必须在房间内开始或结束。

但是，我们有三间有五面墙的房间。该问题解的线有一个起点和一个终点，因此它可以穿过其中两个房间的所有五面墙。然而，由于线已经到达了终点，线不能穿过第三个五墙房间的所有墙壁。因此，在遵守规则的情况下不能画出该问题解的线。