联系

切触形式是奇数维流形上的1度的特殊微分形式；切触变换是坐标的相关变化，在经典力学中具有重要意义。

流形之间的切触经常在奇点理论中进行研究，其中切触的类型被分类为A系列（A₀：相交， A₁：正切， A₂：密切，……）和与球体高度接触的脐或者称D 系列。

在平面中相交于一点 p 的两条曲线：

• 如果曲线有简单的相交（非切线），则为零阶切触。
• 如果两条曲线 相切，则为一阶切触。
• 如果曲线的 曲率相等，则为二阶切触。这种曲线据说是密切的。
• 如果曲率的导数相等，则为三阶切触。
• 如果曲率的二阶导数相等，则为四阶切触。

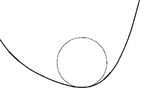
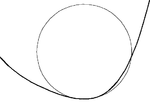
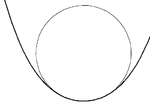
2.1 曲线和圆之间的切触

具有一阶切触（相切的）的圆。

具二阶切触（密切的）的圆。有j

在曲线的顶点处具有三阶切触的圆。

对于光滑平面曲线S上的每一个点 S（t），正好有一个密切圆，其半径是κ（t）的倒数在 t 处的S 的曲率 。当曲率为零（在曲线的拐点处），密切圆是直线。 所有密切圆所在的中心（也称为“曲率中心”）是曲线的渐屈线 。

如果曲率κ'（t）的导数为零，那么密切圆将具有三阶切触，并且曲线被称为具有顶点。渐屈线将在圆心处有一个尖点。曲率的二阶导数的符号决定了曲线具有局部最小或者最大曲率。所有闭合曲线将至少有四个顶点，两个最小值和两个最大值（即四顶点定理）。

一般来说，曲线不会与任何圆有四阶切触。然而，四阶切触一般可以在单参数曲线族中出现，在单参数曲线族中的一条曲线上（随着参数的变化），两个顶点（一个最大值，一个最小值）聚集在一起并湮灭。在这些点上，曲率的二阶导数为零。

2.2 计量经济学中的双切线

在计量经济学中，也可以考虑在曲线上与两个点S（t₁）， S（t₂）有两点切触的圆。这样的圆是双切线 圆。所有双切线圆的中心形成对称集。中轴是对称集的子集。巴西和英国经济学家马里奥·恩里克·西蒙森将这些集合用作表征生物物体形状的方法。