贪心算法

一般来说，贪婪算法有五个组成部分:

1. 一个候选集：从中创建一个解决方案
2. 一个选择函数：用于选择要添加到解决方案中的最佳候选项
3. 一个可行性函数：用于确定候选项是否可以为解决方案做出贡献
4. 一个目标函数：为解决方案或部分解决方案赋值
5. 解决方案函数：它将指示我们何时发现了完整的解决方案

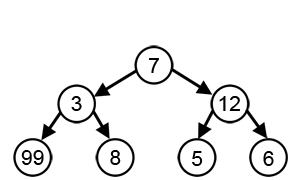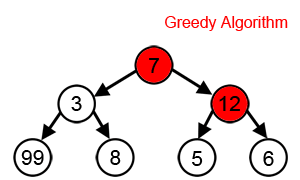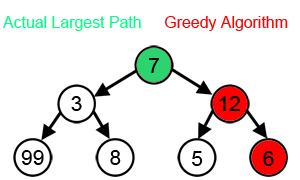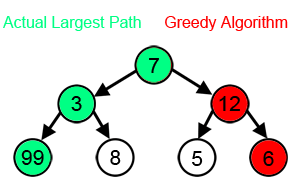
贪婪算法对一些数学问题能够产生很好的解决方案，但对另一些其他数学问题却没有。他们解决的大多数问题都有两个属性:

贪婪选择的属性

我们可以做出目前看来最好的选择，然后解决以后出现的子问题。贪婪算法做出的选择可能取决于迄今为止做出的所有选择，但不取决于未来的选择或子问题的所有解决方案。它反复地做出一个又一个贪婪的选择，把每个给定的问题都简化成一个较小的问题。换句话说，贪婪的算法从不重新考虑它的选择。这也是与动态编程的主要区别，动态编程是详尽的，并且保证能够找到解决方案。在每个阶段之后，动态编程基于前一阶段做出的所有决策做出决策，并且可能会重新考虑前一阶段的算法求解路径。

最优子结构

"如果问题的最优解包含子问题的最优解，则该问题表现出最优子结构."    ^[2]

1.1 失败案例

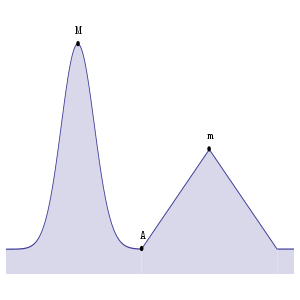
举例说明贪婪算法可能无法达到最优解

从A开始，一个贪婪算法试图通过最大斜率来求最大值，它会在“m”处找到局部最大值，而忽略了“m”处的全局最大值。

贪婪算法以达到最大和为目标，在每一步都会选择看起来是最优的即时选择，所以在第二步会选择12而不是3，不会得到包含99的最优解。

对于许多其他问题，贪婪算法无法产生最优解，甚至可能产生唯一的最坏可能的解。一个例子是上面提到的旅行推销员问题:对于每一个城市数量，都有一个城市之间的距离分配，对于这个分配，最近邻启发式产生了唯一的最坏可能的旅行。^[3]

贪婪算法可以被描述为“短视的”，也可以被描述为“不可恢复的”。它们仅适用于具有“最佳子结构”的问题。尽管如此，对于许多简单的问题，最适合的算法是贪婪算法。但是更需要注意的是，贪婪算法可以用作选择算法，在搜索中对选项进行优先排序，或者分支定界算法。贪婪算法有一些变化:

• 纯贪婪算法
• 正交贪婪算法
• 宽松贪婪算法

贪婪算法在组合优化和理论计算机科学领域有着悠久的研究历史。众所周知，贪婪启发式在许多问题上产生次优结果，^[4] 所以自然的问题是:

• 贪婪算法在哪些问题上表现最佳？
• 对于哪些问题，贪婪算法保证了近似最优的解决方案？
• 对于哪些问题，贪婪算法保证不会产生最优解？

有大量的文献回答了一般类问题，如拟阵，以及特殊问题，如集合覆盖。

3.1 拟阵

拟阵是一种数学结构，它将线性无关的概念从向量空间推广到任意集合。如果一个优化问题具有拟阵结构，那么适当的贪婪算法将使其得到最优解。^[5]

3.2 子模块函数

函数    定义在集合的子集上    叫做 子模型 如果每个    我们有   。

假设有人想找一套    最大化   。贪婪算法，建立一个集合    通过增量地添加的元素    每一步最多产生一个至少为   的集合作为输出。^[6] 也就是说，贪婪在一个常数因子内执行    和最优解一样好。

当对输出施加额外的约束，例如基数约束^[7] ，尽管通常需要对贪婪算法进行细微的改变，但类似的保证也是可以实现的。

3.3 担保的其他问题

贪婪算法提供了强有力的保证但不是最优解的其他问题包括

• 设置封面
• 斯坦纳树问题
• 负载平衡^[8]
• 独立集

许多这些问题都有匹配的下限；即，在最坏的情况下，贪婪算法没有比保证的性能好。

贪婪算法大多(但不总是)无法找到全局最优解，因为它们通常不会对所有数据都进行彻底的操作。他们可能过早地做出某些选择，这妨碍了他们以后找到最优解。例如，所有已知的图着色问题和所有其他NP完全问题的贪婪着色算法都不能始终找到最优解。然而，它们是有用的，因为它们很快就能想出，并且经常给出很好的近似最优解。

如果贪婪算法能够被证明为给定问题类产生全局最优，它通常会成为选择的方法，因为它比其他优化方法(如动态规划)更快。这种贪婪算法的例子是用于寻找最小生成树的克鲁斯卡尔（Kruakal）算法和普林（Prim）算法，以及用于寻找最优霍夫曼树（Huffman trees）的算法。

贪婪算法也出现在网络路由中。使用贪婪路由，消息被转发到离目的地“最近”的相邻节点。节点位置的概念(以及因此的“接近度”)可以由它的物理位置来确定，如在自组织网络使用的地理路由中。在区域路由和分布式哈希表中，位置也可以是完全人工构建的。

• 活动选择问题是这类问题的特征，其目标是选择最大数量的相互不冲突的活动。
• 麦金塔电脑游戏水晶探索的目标是收集水晶，其方式类似于旅行推销员的问题。该游戏有一个演示模式，游戏使用贪婪算法进入每个水晶。人工智能不考虑障碍，所以演示模式经常很快结束。
• 匹配追踪是贪婪算法应用于信号逼近的一个例子。
• 贪婪算法找到了马尔法蒂问题的最优解，即在给定三角形内找到三个不相交的圆，使圆的总面积最大化；据推测，相同的贪婪算法对于任意数量的圆都是最优的。
• 在哈夫曼编码过程中，贪婪算法被用来构造哈夫曼树，在哈夫曼树中找到最优解。
• 在决策树学习中，贪婪算法是常用的，但是它们不能保证找到最优解。
  • 一种流行的这样的算法是决策树构造的ID3算法。
• 迪克斯特拉算法和相关的A*搜索算法是用于图搜索和最短路径搜索的可验证的最优贪婪算法。
  • 搜索是有条件优化的，需要一个不会高估路径成本的“可接受的启发式算法”。
• 克鲁斯卡尔算法和普林算法是构造给定连通图的最小生成树的贪婪算法。他们总是会找到一个最佳的解决方案，而这个解一般情况下可能不是唯一的。