普里姆算法
编辑在计算机科学中,普里姆(也称为Jarník's)算法是一种贪婪算法,它为加权的无向图找到一个最小生成树 。这意味着它找到边的一个子集,能够形成了一个包括所有顶点的树,其中在树中所有边的权重总和最小。该算法通过从任意起始顶点开始一次给树增加一个顶点来操作,在每个步骤中添加从树到另一个顶点的花费最小的可能的连接。
该算法由捷克数学家沃伊茨奇·贾尼克于1930年开发[1]后,后来在1957年被计算机科学家罗伯特·普里姆,以及在1959年被艾兹赫尔·戴克斯特拉[2]重新发现和重新出版[3]。因此,它有时也被称为Jarník算法,[4] 普里姆-jarník算法,[5] 普里姆-迪克斯特拉算法[6]或者DJP算法。[7]
这个问题的其他众所周知的算法包括克鲁斯卡尔算法和 Borůvka's算法。[8]这些算法在一个可能的非连通图中找到最小生成森林;相比之下,普里姆算法最基本的形式只能在连通图中找到最小生成树。然而,为图中的每个连通分量单独运行普里姆算法,也可以用于找到最小生成森林。[9]就渐近时间复杂度而言,这三种算法对于稀疏图来说速度相同,但比其他更复杂的算法慢。[7][6]然而,对于足够密集的图,普里姆算法可以在线性时间内运行,满足或改进其他算法的时间限制。
1 描述编辑
该算法可以非正式地描述为执行以下步骤:
- 从图中任意选择一个顶点,然后用这个顶点初始化一颗树。
- 把这棵树增加一条边:在满足能将树和不在树中的顶点连接起来的所有边中,找到而且具有最小的权重的边,然后把这条边增加到树里面。
- 重复步骤2(直到所有顶点都包含在树中)。
更详细地说,它可以按照下面的伪代码语句实现。
- 在图中把每个顶点 v 都关联一个数C[v] (表示连接"v"的最小花费)和一条边E[v](有着最小花费的连接的边)。要初始化这些值,首先将所有的C[v] 设为 +∞(或者任何比图中最大边权重更大的数值)以及将每条边设为一个特殊的标记值,从而表示"v"和之前的顶点之间没有边连接。
- 初始化一个空的森林"F"和未被包含进"F"的顶点的集合"Q"(初始状态下是所有的顶点)。
- 重复下面的步骤直到Q 为空为止:
- 从 Q 中找到具有最小可能值C[v]的顶点"v"并将其从集合中移出
- 将 v 加入到 F 中,如果E[v] 不是标记值,那么将 E[v] 也加入到 F中
- 在边vw 上进行循环,从而将 v 连接到其他的顶点 w上。. 对于每条这样的边, 如果if w 仍然属于 Q 并且 vw 的权重要比 C[w]小, 那么执行以下步骤:
- 将C[w] 设为边 vw的花费
- 用 E[w] 来指向边 vw。
- 返回 F
如上所述,算法的起始顶点将被任意选择,因为算法主循环的第一次迭代中在Q中将有一组顶点权重相等,当算法将输入图的每个连接部分都构成生成树时,它会自动在F中生成一颗新的树。该算法可以通过设置C[s]小于C的其他任何值(例如,为零),从而修改为可以从任何特定顶点s开始,并且它可以修改为只找到一个生成树,而不是整个生成森林(与非正式描述更加符合),方法是每当遇到标记为没有关联边的另一个顶点时就停止。
算法的不同变体在集合Q的实现方式上互不相同:实现为简单的链表或顶点数组,或更复杂的优先队列数据结构。这种选择导致算法的时间复杂度不同。一般来说,优先级队列会更快找到有着最小的花费的顶点v,但当C[w]的值变化时更新的时间会很长。
2 时间复杂度编辑
普里姆算法的时间复杂度取决于图和按权重排序边的数据结构,这两个都可以使用优先队列来完成。下表显示了典型的选择:
| 最小边权重数据结构 | 时间复杂度(总计) |
|---|---|
| 邻接矩阵,搜索 | |
| 二叉堆和邻接表 | |
| 斐波那契堆和邻接表 |
普里姆有的一种简单实现,是通过使用邻接矩阵或邻接表来进行图表示,并用线性搜索权重数组以找到要添加的最小权重边,这种实现需要 O (|V|2)运行时间。然而,通过使用堆来实现在算法的内部循环中找到最小权重边,可以大大提高运行时间。
第一个改进版本使用堆来存储输入图的所有边,按照它们的权重排序。使得它有着最坏情况下O(|·E·|·log |·E·|)的运行时间。但是利用存储顶点而不存储边的方式可以对它进行进一步地改善。在堆中,应该按照将顶点连接到部分构造的最小生成树(MST)的任何顶点的最小边权重(如果不存在这样的边,则为无穷大)来排序顶点。每次选择顶点v并添加到MST中时,会对在部分MST之外的所有顶点w执行键的逆序排序操作,使得v连接到w,将键对应的值设置为其先前值的最小值和边(v,w)的花费。
使用一个简单的二叉堆数据结构,普里姆算法当前可以在时间 O (|E|log|V|)内运行,其中|E|是边的数量,|V|是顶点的数量。使用更复杂的斐波那契堆,时间复杂度可以减少为为 O (|E|+|V|log|V|),这个方法在当图表足够稠密满足|E|等于 ω (|V|)时渐近更快,并且当|E|至少是 |V| log |V|时,这个方法会只花费线性时间。对于密度更大的图(至少有|V|c 条边,其中c > 1),普里姆算法甚至可以通过简单地使用d-堆代替斐波那契堆,从而在线性时间运行。[10][10]
3 正确性证明编辑
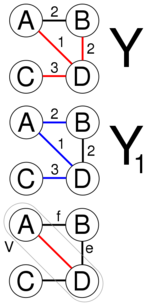
令P为一个加权连通图。在普里姆算法的每次迭代中,都必须找到一条边,将子图中的顶点连接到子图外部的顶点。因为P是连通的,到每个顶点都存在一条路径。普林姆算法的输出Y是一棵树,因为添加到树Y中的边和顶点是连接起来的。令Y1为图P的最小生成树。如果Y1=Y那么Y就是最小生成树。否则,让e是在构建不等于Y1的Y树的过程中添加的第一条边,且V是在边e之前添加的由边连接起来的顶点的集合。那么边e的一个端点属于V,另一个不属于。因为树Y1是图P的生成树,所以树Y1上存在一条路径连接两个端点。当沿着路径行进时,一定会遇到一条边f连接集合V中的一个顶点到一个不在集合V中的顶点。现在,在边e被添加到树中Y的迭代中,边缘f也可以被添加进来,并且如果它的权重小于e,那么将添加它而不是边e,我们得出结论
让树Y2是从树Y1去除边f并添加边e得到的图。很容易能表示出树Y2是连通的,与树Y1具有相同的边数,其边的总权重不大于树的Y1总权重,因此,它也是图P的最小生成树,并且它包含边缘e以及在构造集合V时在它之前添加的所有边。重复上述步骤,我们最终将从图P中获得一个和树Y一样的最小生成树。这表明Y是最小生成树。最小生成树允许子区域的第一子集扩展成为更小的、并假设是最小的子集X。
4 并行算法编辑
普里姆算法的主循环本质上是顺序的,因此是不可并行化的。然而,在中确定不形成循环的最小权重的下一个边是可以通过在可用处理器之间划分顶点和边来并行化的。[11]下面的伪代码语句演示了这一点。
- 给每个处理器分配 一个长度为 的连续顶点集合 。
- 像在顺序算法中一样创建C, E, F, 和Q ,并且与在处理器中划分图一样来划分C, E,从而使得每个处理器都存有它的顶点集合的进入边。令 , 表示在处理器 存储的C, E的那一部分。
- 重复以下步骤直到 Q 为空:
- 在每个处理器上:找到在 [ ] (局部解)中具有最小值的顶点 。
- 在局部解上最小归约 来找到有着最小可能值C[v] (全局解)的顶点v 。
- 广播 被选择的节点到每个处理器上。
- 将v 添加到 F 中,如果E[v] 不是特殊的标记值,那么将 E[v] 也添加到 F中。
- 在每个处理器上:就像在顺序的算法中一样更新 和 。
- 返回 F
该算法通常可以在分布式机器上[11]以及共享内存机器上实现。[12]这个算法也已经在图形处理单元(GPU)上实现。[13]运行时间是 ,假设归约和广播操作可以在 中执行。[11]在共享内存机器中的一个普里姆算法变体,其中普里姆的顺序算法从不同的顶点开始并行运行的机制也被探索过。[14]然而,应该注意到存在更复杂的算法来以更有效的方式解决分布式最小生成树问题。
参考文献
- [1]
^Jarník, V. (1930), "O jistém problému minimálním" [About a certain minimal problem], Práce Moravské Přírodovědecké Společnosti (in 捷克语), 6 (4): 57–63。.
- [2]
^Dijkstra, E. W. (December 1959), "A note on two problems in connexion with graphs" (PDF), Numerische Mathematik, 1 (1): 269–271, CiteSeerX 10.1.1.165.7577, doi:10.1007/BF01386390。.
- [3]
^Prim, R. C. (November 1957), "Shortest connection networks And some generalizations", Bell System Technical Journal, 36 (6): 1389–1401, doi:10.1002/j.1538-7305.1957.tb01515.x。.
- [4]
^Sedgewick, Robert; Wayne, Kevin Daniel (2011), Algorithms (4th ed.), Addison-Wesley, p. 628, ISBN 978-0-321-57351-3。.
- [5]
^Rosen, Kenneth (2011), Discrete Mathematics and Its Applications (7th ed.), McGraw-Hill Science, p. 798。.
- [6]
^Cheriton, David; Tarjan, Robert Endre (1976), "Finding minimum spanning trees", SIAM Journal on Computing, 5 (4): 724–742, doi:10.1137/0205051, MR 0446458。.
- [7]
^Pettie, Seth; Ramachandran, Vijaya (January 2002), "An optimal minimum spanning tree algorithm" (PDF), Journal of the ACM, 49 (1): 16–34, CiteSeerX 10.1.1.110.7670, doi:10.1145/505241.505243, MR 2148431。.
- [8]
^Tarjan, Robert Endre (1983), "Chapter 6. Minimum spanning trees. 6.2. Three classical algorithms", Data Structures and Network Algorithms, CBMS-NSF Regional Conference Series in Applied Mathematics, 44, Society for Industrial and Applied Mathematics, pp. 72–77。.
- [9]
^Kepner, Jeremy; Gilbert, John (2011), Graph Algorithms in the Language of Linear Algebra, Software, Environments, and Tools, 22, Society for Industrial and Applied Mathematics, p. 55, ISBN 9780898719901。.
- [10]
^Tarjan(1983),p . 77..
- [11]
^Grama, Ananth; Gupta, Anshul; Karypis, George; Kumar, Vipin (2003). Introduction to Parallel Computing. pp. 444–446. ISBN 978-0201648652..
- [12]
^Quinn, Michael J.; Deo, Narsingh (1984). "Parallel graph algorithms". ACM Computing Surveys (CSUR) 16.3: 319–348..
- [13]
^Wang, Wei; Huang, Yongzhong; Guo, Shaozhong (2011). "Design and Implementation of GPU-Based Prim's Algorithm". International Journal of Modern Education and Computer Science 3.4..
- [14]
^Setia, Rohit (2009). "A new parallel algorithm for minimum spanning tree problem". Proc. International Conference on High Performance Computing (HiPC)..
暂无