贡献者: addis; JierPeter
简单来说,连续函数定义为:在某个区间内,函数曲线是连续的。例如常见的 $\sin x$,$\exp x$,$x^2$ 都在整个实数域上连续,又例如 $\ln x$ 和 $1/x$ 在区间 $(0, \infty)$ 上连续,$\tan x$ 在所有 $x_n = (1/2 + n)\pi$($n$ 为自然数)处不连续,$1/x$ 在 $x = 0$ 处不连续。但这只是一些简单的情况。在一些情况下这种判断方法则显得不严谨,例如函数
\begin{equation}
f(x) = \left\{\begin{aligned}
& \sin\left(1/x\right) \quad &(x \ne 0)\\
&0 \quad &(x = 0)
\end{aligned}\right. ~.
\end{equation}
在原点处的连续性(不连续)根据这个定义不好判断。所以我们需要一个更严谨的定义。
首先我们要讨论函数在一个点附近是否是连续的。这个概念的思想核心是,在函数曲线的某一点附近 $(x_0, f(x_0))$,无论我们要求 $f(x)$ 有多接近 $f(x_0)$,只要 $x$ 足够靠近 $x_0$,就一定能满足条件。比如说,如果定义函数 $f$ 为当 $x<0$ 的时候,$f(x)=0$,其它时候 $f(x)=1$,那么在 $x=0$ 这一点处 $f$ 就是跳跃的。如果我们要求的接近程度小于 $1$,那么无论 $x$ 多接近 $0$,只要 $x<0$,$f(x)$ 和 $f(0)=1$ 的距离就永远满足不了需要。
准确地描述以上 “连续” 的概念,如下所示:
定义 1 函数在一点的连续性和区间的连续性
函数 $f(x)$ 在某点 $x = x_0$ 处连续的定义是:函数 $f(x)$ 在某点 $x=x_0$ 处连续,当且仅当对于任何精度要求 $\epsilon>0$,我们都可以找到一个对应的范围 $\delta>0$,使得只要 $|x-x_0|<\delta$,就有 $|f(x)-f(x_0)|<\epsilon$。用极限符号来表示,就是:
\begin{equation}
\lim_{x \to x_0} f(x) = f(x_0)~.
\end{equation}
如果一个函数在某区间的所有点都连续,我们就说它在这个区间连续。
注意这里要求 $x$ 从左边和右边趋近于 $x_0$ 时的极限(即左极限和右极限)都成立。
1. 一致连续
以上所定义的连续性是针对一个个点 $x_0$ 而言的,就算函数在每一个点都连续,我们也只能说这个函数是逐点连续的(pointwise continuous)。事实上,还有一种更强的连续性,它着眼于整体的性质,这就是一致连续(uniformly continuous)。它的准确定义如下:
定义 2 一致连续
如果函数 $f(x)$ 在区间 $S$ 上,对于任意精度 $\epsilon>0$,都存在对应的范围 $\delta>0$,使得只要 $|x_1-x_2|<\delta$,那么 $|f(x_1)-f(x_2)|<\epsilon$。
一致连续着眼于整个区间的性质,而不是一个个点。显然,一致连续的函数肯定逐点连续,但是逐点连续的函数不一定一致连续,我们举一个反例。
例 1
例如考虑函数 $f(x)=1/x$,那么在区间 $(0, \infty)$ 上,$f$ 就是逐点连续的,但它并不一致连续;对于同样的精度要求 $\epsilon>0$ 和任何范围 $\delta>0$,只要 $0< x_1<\delta$,那么就总有一个足够小的 $x_2$ 使得 $|f(x_1)-f(x_2)|>\epsilon$,毕竟当 $x_2$ 接近 $0$ 的过程中,$f(x_2)$ 的斜率绝对值会趋近于无穷大。
习题 1 连续但不一致连续的函数
试证明 $1/x$ 在区间 $(0, +\infty]$ 以及 $x^2$ 在 $\mathbb R$ 都是连续的,但不是一致连续的。
定理 1
设 $S$ 是 $\mathbb{R}$ 的一个区间。函数 $f$ 在 $S$ 上逐点连续的充分必要条件是,对于任何开区间 $A\subset \mathbb{R}$,满足 $f(x)\in A$ 的所有 $x$ 构成的集合,是若干开区间的并集。用紧凑的写法来表达就是,$f^{-1}(A)$ 是开区间的并集。
这个定理还可以等价地用闭区间来表达:$f$ 在 $S$ 上逐点连续的充分必要条件是,任何闭区间的逆映射是闭区间的并集。
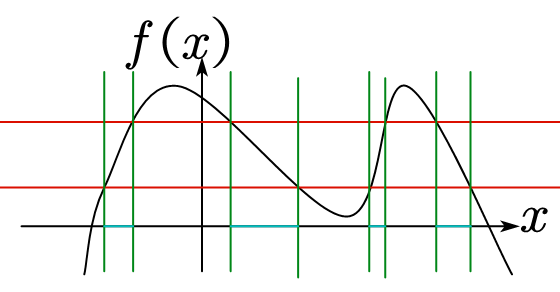
图 1:如图,红色水平线在 $f(X)$ 轴上划分出了一个开/闭区间,绿色垂直线是取反函数的过程,$x$ 轴上的靛蓝色线段就是取反函数的结果。从这个图可以直观地看出
定理 1 的意义。
在实数轴上,开集被定义为任何开区间的并集,而闭集是开集的补集。如果 $S$ 是 $\mathbb{R}$ 的一个子集,那么 $S$ 上的开集被定义为 $\mathbb{R}$ 的开集和 $S$ 的交集。这样一来,定理 1 就可以扩展为:$f$ 在 $S$ 上逐点连续,等价于对于任何开集 $A$,$f^{-1}(A)\cap S$ 是 $S$ 上的开集,等价于对于任何闭集 $B$,$f^{-1}(B)\cap S$ 是 $S$ 上的闭集。
用逆映射来刻画连续性是一个非常好用的方法。
致读者: 小时百科一直以来坚持所有内容免费,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 10 元,我们一个星期内就能脱离亏损, 并保证在接下来的一整年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。