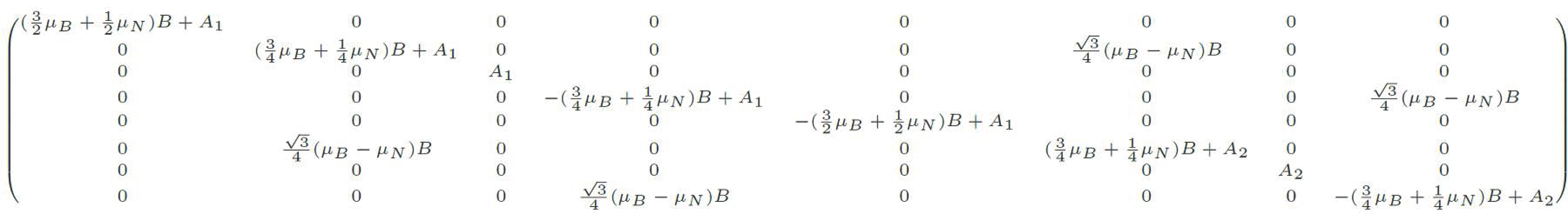贡献者: addis
研究冷原子主要是两方面(其中后者更重要):原子的内部结构,和原子原子之间的相互作用。
首先研究原子内部结构,我们可以先写出单原子的 Hamiltonian,
\begin{equation}
\begin{split}
\hat{H}_{at}=&-\sum_i\left(\frac{\hbar^2\nabla_i^2}{2\mu_i}+V_{ei}({ \boldsymbol{\mathbf{r}} })\right) + \sum_{i< j}V_{ee}({ \boldsymbol{\mathbf{r}} }_i-{ \boldsymbol{\mathbf{r}} }_j)\\
&+\sum_i [\alpha_f { \boldsymbol{\mathbf{S}} }_i\cdot{ \boldsymbol{\mathbf{L}} }_i+\alpha_{hf}({ \boldsymbol{\mathbf{S}} }_i+{ \boldsymbol{\mathbf{L}} }_i)\cdot { \boldsymbol{\mathbf{I}} }_i]~.
\end{split}
\end{equation}
如果只考虑第一项,也就是说每个电子之间是没有相互作用的,得到的是很经典的能级,我们中学就学过。第二项的作用是给了一个修正,当然一般的表达式并不容易写出来,但是我们知道能量的修正可以写成如下形式
\begin{equation}
E = -\frac{\mu\alpha^2}{2\hbar^2(n+\Delta)^2}~,\quad \Delta = \Delta(n,l)~,\quad \alpha = \frac{e^2}{4\pi\varepsilon_0}~.
\end{equation}
除此之外,第二项还能提供一个我们所知的 Hund 规则,单重态 $\psi_1({ \boldsymbol{\mathbf{r}} }_1)\psi_2({ \boldsymbol{\mathbf{r}} }_2)-\psi_1({ \boldsymbol{\mathbf{r}} }_2)\psi_2({ \boldsymbol{\mathbf{r}} }_1)$ 在离的很近的时候波函数是基本没有的,也就是提供了一个 repulsive 的能量;这也就是说三重态相比单重态能量更低。
第三项,正如他的名字所暗示的,包含着精细结构(fine)和超精细结构(hyperfine)
原子物理里面,一个很基本的概念就是 Zeeman 效应,这是实验上观测到,并在后来基于量子理论建立了正确的描述;很通俗而且愚蠢的 Zeeman 项(系数)的解释是:相对的,原子核(带电)绕电子转圈,引发磁场,与电子的自旋相互作用。
\begin{equation}
E\propto -{ \boldsymbol{\mathbf{\mu}} }_s\cdot{ \boldsymbol{\mathbf{B}} }_{\text{eff}}=\frac{Ze^2\mu_0}{8\pi m_0^2 r^3}({ \boldsymbol{\mathbf{S}} \cdot L})~.
\end{equation}
这一项相比与之前大概是 $10^{-3}$ 的量级;而电子整体的角动量与核自旋的相互作用是超精细结构,相比精细结构是 $10^{-3}$ 的量级。
物理学对原子进行分类,主要有三类(实际上有很多更精细的分化,但在冷原子范畴内我们并不关心原子形成的晶体的结构:我们希望在极低温度的情况下,原子仍然能保证不会结晶而是气态;这也是冷原子的密度极低,十分稀薄从而少体散射就适用的一个原因):
碱金属:锂钠钾铷铯钫。$^{2S+1}L_J$ 表示的话,这些原子的基态都是 $^2 S_{1/2}$,价电子都是 $ns^1$,区别主要体现在核自旋上(不同的同位素)。$^{87}\text{Rb}, ^{23}\text{Na}$ 是最常见最爱研究的玻色气体,而 $^{40}\text{K}, ^6 \text{Li}$ 则是最常见的费米气体。Fermion or Boson 主要看核自旋是整数还是半整数。
作为例子看一个问题:
$^{87}{\text{Rb}}, ^6{\text{Li}}$ 在磁场 $ \boldsymbol{\mathbf{B}} = B \hat{\boldsymbol{\mathbf{z}}} $ 中,Hamiltonian 可以写成
\begin{equation}
\hat{H} = B(\mu_B J_z+\mu_N I_z)+\alpha({ \boldsymbol{\mathbf{J}} \cdot I})~.
\end{equation}
这个的处理方法实际上和传统的 $LS$ 耦合基本一样:引入一个新的参数 ${ \boldsymbol{\mathbf{F}} = J+I}$,从而保证
\begin{equation}
{ \boldsymbol{\mathbf{J}} \cdot I} = \frac{1}{2}({ \boldsymbol{\mathbf{F}} }^2 - { \boldsymbol{\mathbf{J}} }^2 - { \boldsymbol{\mathbf{I}} }^2) = \frac{1}{2} (F(F+1) - J(J+1) - I(I+1))~,
\end{equation}
从而能谱就是
\begin{equation}
E = B(\mu_B J_z+\mu_N I_z)+\frac{\alpha}{2} (F(F+1) - J(J+1) - I(I+1))~.
\end{equation}
除此之外,我们还可以看到另外的东西。这个 Hamiltonian 不好解,但是我们可以用 $|F,m_F\rangle$ 来展开,并且把超精细结构的项作为 perturbation 来处理。$^{87}{\text{Rb}}: I = \frac{3}{2};\ ^6{\text{Li}}: I = 1; J = \frac{1}{2}$
对于 $^{87}{\text{Rb}}$ 来说,能够得到的 $F=2,1$。其本征态有两系列
$F=2:|2,0\rangle,|2,\pm1\rangle,|2,\pm2\rangle~,$
$F=1:|1,0\rangle,|1,\pm1\rangle~.$
但是我们知道,$|F,m_F\rangle$ 必须利用 $CG$ 系数知道它实际上是如何被组合成的,才能用我们的 Hamiltonian 计算。
\begin{align}
& \left\lvert 2,2 \right\rangle = \left\lvert \frac{3}{2},\frac{3}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle ~,\\
& \left\lvert 2,1 \right\rangle = \frac{1}{2} \left\lvert \frac{3}{2},\frac{3}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle + \frac{\sqrt{3}}{2} \left\lvert \frac{3}{2},\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle ~,\\
& \left\lvert 2,0 \right\rangle = \frac{\sqrt{2}}{2} \left\lvert \frac{3}{2},\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle + \frac{\sqrt{2}}{2} \left\lvert \frac{3}{2},-\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle ~,\\
& \left\lvert 2,-1 \right\rangle = \frac{1}{2} \left\lvert \frac{3}{2},-\frac{3}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle + \frac{\sqrt{3}}{2} \left\lvert \frac{3}{2},-\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle ~,\\
& \left\lvert 2,-2 \right\rangle = \left\lvert \frac{3}{2},-\frac{3}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle ~,\\
& \left\lvert 1,1 \right\rangle = \frac{\sqrt{3}}{2} \left\lvert \frac{3}{2},\frac{3}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle - \frac{1}{2} \left\lvert \frac{3}{2},\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle ~,\\
& \left\lvert 1,0 \right\rangle = \frac{\sqrt{2}}{2} \left\lvert \frac{3}{2},\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle - \frac{\sqrt{2}}{2} \left\lvert \frac{3}{2},-\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle ~,\\
& \left\lvert 1,-1 \right\rangle = -\frac{\sqrt{3}}{2} \left\lvert \frac{3}{2},-\frac{3}{2} \right\rangle \left\lvert \frac{1}{2},\frac{1}{2} \right\rangle + \frac{1}{2} \left\lvert \frac{3}{2},-\frac{1}{2} \right\rangle \left\lvert \frac{1}{2},-\frac{1}{2} \right\rangle ~.
\end{align}
这样写出来的 Hamiltonian 是一个 $8\times8$ 的矩阵,当然大部分矩阵元都是 0,但是对角项和一些部分也不是 $0$。利用一些技巧,我们知道只有拥有同样的 $m_F$ 的两个态之间才有矩阵元,凭借惊人的毅力,我们把这个矩阵写出来,如图 1 (本人的计算功底很差…如果算错了不要打我1):
图 1:算错的矩阵
\begin{equation} \begin{aligned}
&A_1\equiv\frac{3}{4}\alpha = \frac{\alpha}{2}\left(2\times3 - \frac{3}{2}\times\frac{5}{2} - \frac{1}{2}\times\frac{3}{2}\right)~,\\
&A_2 \equiv -\frac{5}{4}\alpha = \frac{\alpha}{2}\left(1\times2 - \frac{3}{2}\times\frac{5}{2} - \frac{1}{2}\times\frac{3}{2}\right)~.
\end{aligned} \end{equation}
发现,只有在 $|2,1\rangle,|1,1\rangle$ 和 $|2,-1\rangle,|1,-1\rangle$ 之间存在 off-diagonal 成分。相当于我们需要对角化如下两个 $2\times$ 矩阵:
\begin{equation} \begin{aligned}
\left(
\begin{matrix}
\left(\frac{3}{4}\mu_B+\frac{1}{4}\mu_N\right)B+A_1 & \frac{\sqrt{3}}{4}(\mu_B-\mu_N)B\\
\frac{\sqrt{3}}{4}(\mu_B-\mu_N)B & \left(\frac{3}{4}\mu_B+\frac{1}{4}\mu_N\right)B+A_2
\end{matrix}
\right)~,\\
\left(
\begin{matrix}
-\left(\frac{3}{4}\mu_B+\frac{1}{4}\mu_N\right)B+A_1 & \frac{\sqrt{3}}{4}(\mu_B-\mu_N)B\\
\frac{\sqrt{3}}{4}(\mu_B-\mu_N)B & -\left(\frac{3}{4}\mu_B+\frac{1}{4}\mu_N\right)B+A_2
\end{matrix}
\right)~.
\end{aligned} \end{equation}
得到这两部分的本征值分别应该为
\begin{equation}
\lambda_{1,2/1} = -\left(\frac{3}{4}\mu_B-\frac{1}{4}\mu_N\right)B+\frac{A_1+A_2}{2} \pm \sqrt{\frac{1}{4}(A_1-A_2)^2+\frac{3}{4}(\mu_B-\mu_N)^2B^2}~,
\end{equation}
\begin{equation}
\lambda_{-1,2/1} = \left(\frac{3}{4}\mu_B+\frac{1}{4}\mu_N\right)B+\frac{A_1+A_2}{2} \pm \sqrt{\frac{1}{4}(A_1-A_2)^2+\frac{3}{4}(\mu_B-\mu_N)^2B^2}~.
\end{equation}
这两个本征值的行为在 $B$ 非常小和相对大一点的时候有着截然不同的表现。在很小的时候,也就是说 $B\ll|A_1-A_2| / \sqrt{3}(\mu_B-\mu_N)$,我们可以把根号内进行展开,得到
\begin{equation}
\sqrt{\frac{1}{4}(A_1-A_2)^2+\frac{3}{4}(\mu_B-\mu_N)^2B^2} \approx \frac{1}{2}|A_1-A_2| \left(1+\frac{3}{2}\frac{(\mu_B-\mu_N)^2}{(A_1-A_2)^2}B^2 \right) ~.
\end{equation}
得到了一个 Zeeman \text{eff}ect 的二次 shift。而大的磁场下超精细结构 $A_1, A_2$ 很小,几乎忽略,主要修正项都是 $\frac{\sqrt{3}}{2}\Delta\mu B$,是线性的 Zeeman shift。
当然这只是一个关于二次 Zeeman shift 的例子,$^6{\text{Li}}$ 同理,有兴趣的同学可以进行练习。
碱金属原子的另一个特点就是明显的第一激发态的劈裂。第一激发态本身应该是 $L=1$,也就是 $^2P$。但是如果有了 $LS$ 耦合,不同的 $J$ 会有不同的精细结构劈裂。最简单的就是大家都实验过的 $Na$ 黄光双线。当然如果考虑超精细结构还会更进一步分裂,但是那个效应太小不容易观察到。
要注意,在基态和这两个激发态之间的光跃迁是实验上对(冷)原子进行捕捉和操作的基本手段。冷的目的是他们基本没有很大的动能,这样就少去了很多的复杂因素(反冲能量损失、多普勒效应等)。
最后一类有趣的原子就是高自旋原子。不过我并不对这个感兴趣,就先不写简介了。
接下来讨论一下上面提到的光跃迁过程——说白了就是一个原子在偶极作用下的行为。
光引入的附加 Hamiltonian 是:
\begin{equation}
\hat{H}_d = { \boldsymbol{\mathbf{d}} \cdot E} = d_j E_j^0 \cos\left(\omega t-\phi_j\right) ~,
\end{equation}
其中 ${ \boldsymbol{\mathbf{d}} } = \sum_\alpha (-e{ \boldsymbol{\mathbf{r}} }_\alpha)$,代表原子的偶极矩。
比如,我们研究碱金属的问题。相对的,我们研究的是从 $^2S_{1/2}$ 到 $^2P_{3/2},\ ^2P_{1/2}$ 的跃迁。两个激发态可以用 $D_1,D_2$ 表示,能级差是有精细机构带来的;一个数量级上的能量估计是:$\Delta_{sp} \gg \Delta_f \gg \Delta_{hf}$。显然,这里我们可以忽略掉超精细结构。
我们定义投影算符,把态投影到基态或者激发态上。显然这里可以使用
\begin{equation}
\mathcal{P}_g = \frac{{ \boldsymbol{\mathbf{L}} }^2}{2\hbar}~,\quad \mathcal{P}_e = 1 - \mathcal{P}_g~.
\end{equation}
而体系的 Hamiltonian 在无外场的时候则是
\begin{equation}
\hat{H} = \hat{H}_{at}+\hat{H}_d~.
\end{equation}
我们前面分析了,无外场
\begin{equation}
\hat{H}_{at} = E_e\mathcal{P}_e + \frac{A_{f}}{\hbar^2} \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} ~.
\end{equation}
这个解释就是:我们把基态能量扔了,而且不去管那些关于主量子数 $n$ 的细节;在我们需要考虑的范围内,Hamiltonian 就可以写成你在激发态上的成分乘以激发态的能量 $E_e$。显然,这个 Hamiltonian 并不包含在基态和激发态之间的任何 coupling。
我们定义一个算符
\begin{equation}
\mathcal{U}_{rot}(t) = \mathrm{e} ^{- \mathrm{i} \omega t\mathcal{P}_e} = \mathcal{P}_g + \mathcal{P}_e \mathrm{e} ^{- \mathrm{i} \omega t}~.
\end{equation}
这算符相当于做一个 unitary 的变换
2,我们现在看外场怎样变换
\begin{equation}
\hat{H}_d' = \mathcal{U}_{rot} ^\dagger (t)\hat{H}_d \mathcal{U}_{rot}~,
\end{equation}
显然的,我们知道无论基态还是激发态都没有特殊的极化方向,$\langle d_j \rangle = 0$,即
\begin{equation}
\mathcal{P}_g d_j \mathcal{P}_g = \mathcal{P}_e d_j \mathcal{P}_e = 0~.
\end{equation}
而另一方面,$E_j$ 又是外场,不与投影算符 $\mathcal{P}$ 有对易关系。因此,我们很容易的可以进行一步化简:
\begin{equation}
\hat{H}_d' = E_j^0 \cos\left(\phi_j-\omega t\right) (\mathcal{P}_g d_j \mathcal{P}_e \mathrm{e} ^{- \mathrm{i} \omega t} + \mathcal{P}_e \mathrm{e} ^{ \mathrm{i} \omega t} d_j \mathcal{P}_g)~,
\end{equation}
而
\begin{equation}
\cos\left(\phi_j - \omega t\right) = \frac{ \mathrm{e} ^{ \mathrm{i} (\phi_j-\omega t)} + \mathrm{e} ^{- \mathrm{i} (\phi_j-\omega t)}}{2}~.
\end{equation}
定义 $\tilde{E}_j = E_j^0 \mathrm{e} ^{ \mathrm{i} \phi_j}$,我们得到
\begin{equation}
\hat{H}_d' = \frac{1}{2}\left(\tilde{E}_j \mathrm{e} ^{- \mathrm{i} \omega t} + \tilde{E}_j^* \mathrm{e} ^{ \mathrm{i} \omega t}\right) (\mathcal{P}_g d_j \mathcal{P}_e \mathrm{e} ^{- \mathrm{i} \omega t} + \mathcal{P}_e \mathrm{e} ^{ \mathrm{i} \omega t} d_j \mathcal{P}_g)~.
\end{equation}
在近似共振的时候 $\omega\sim\omega_e = E_e/\hbar$,某种程度上可以忽略到以 $\pm 2 \mathrm{i} \omega t$ 做震荡的成分(被称为 Rotating Wave Approximation RWA3),于是我们得到
\begin{equation}
\hat{H}_d' \approx \frac{1}{2}\left(\tilde{E}_j\mathcal{P}_e d_j \mathcal{P}_g + \tilde{E}_j^*\mathcal{P}_g d_j \mathcal{P}_e\right)~.
\end{equation}
因为包含精细结构 $A_f \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} /\hbar^2$ 的项已经很小了,其在这个 Unitary 变换下的变化可以忽略。而另一方面,一个 unitary 的变换,如果是含时的,则会带来一个变化,是由于要保证 Hamiltonian 的定义正确4
\begin{equation}
|\psi\rangle \to \mathcal{U}(t)|\psi\rangle = |\psi'\rangle~,
\end{equation}
\begin{equation}
H'|\psi'\rangle = \mathrm{i} \hbar\frac{d}{dt}|\psi'\rangle = \mathrm{i} \hbar\frac{d \mathcal{U}(t)}{dt}|\psi\rangle + \mathrm{i} \hbar\mathcal{U}(t) \frac{\mathrm{d}}{\mathrm{d}{t}} |\psi\rangle~.
\end{equation}
而 $|\psi\rangle = \mathcal{U} ^\dagger (t)|\psi'\rangle$,故
\begin{equation}
H'|\psi\rangle = \left( \mathrm{i} \hbar\frac{d\mathcal{U}(t)}{dt}\mathcal{U} ^\dagger (t) + \mathcal{U}(t)H\mathcal{U} ^\dagger (t)\right)|\psi'\rangle ~.
\end{equation}
从而
\begin{equation}
H'= \mathrm{i} \hbar\frac{d\mathcal{U}(t)}{dt}\mathcal{U} ^\dagger (t) + \mathcal{U}(t)H\mathcal{U} ^\dagger (t)~,
\end{equation}
\begin{equation}
\hat{H}'_{at} = E_e \mathcal{P}_e - \hbar\omega\mathcal{P}_e + \frac{A_{f}}{\hbar^2} \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} ~.
\end{equation}
我们研究对基态的二阶微扰。微扰理论的基本知识可以参考 Prof Fa, Wang 的讲义,见 Fa Wang5。
能量的修正应该是
\begin{equation}
\Delta E = \langle g|H_d'|g\rangle + \frac{\langle g|H_d'|e\rangle \langle e|H_d'|g\rangle}{0-E_e'}~.
\end{equation}
可以一目了然的看出来,$H_d'$ 这种左边右边有不同的投影算符 $\mathcal{P}$ 的,第一项为 0;而第二项可以简化成
\begin{equation}
\Delta E = - \langle g|H_d'|e\rangle H'^{-1}_{at} \langle e|H_d'|g\rangle~.
\end{equation}
因为这里我们实际上扔了一个算符进去,并不应该写成这样子,而应该写成一个仅对基态有用的有效 Hamiltonian:
\begin{equation}
H_{\text{eff}} = -\mathcal{P}_g H_d' \mathcal{P}_e H'^{-1}_{at} \mathcal{P}_e H_d' \mathcal{P}_g \sim -\mathcal{P}_g H_d' H'^{-1}_{at} H_d' \mathcal{P}_g ~,
\end{equation}
其中近似是由于:我们只希望得到二阶的修正,所以 $H_{at}'$ 基本只作用在激发态上,两个对激发态的投影算符可以忽略了。
来咱们继续,虽然发生了很多令人伤心的事情但是冷原子的学习还是要继续的。
我们定义一个二阶矩阵(算符):
\begin{equation}
\mathcal{D}_{ij} = \mathcal{P}_g d_i \hat{H}_{at}^{-1} d_j \mathcal{P}_g ~.
\end{equation}
这样的话,考虑到
\begin{equation} \begin{aligned}
\hat{H}_{\text{eff}} &= -\mathcal{P}_g \hat{H}_d' \hat{H}'^{-1}_{at} \hat{H}_d' \mathcal{P}_g\\
&= -\frac{1}{4} \mathcal{P}_g \left({\color{red}{\tilde{E}_j\mathcal{P}_e d_j \mathcal{P}_g}} + \tilde{E}_j^*\mathcal{P}_g d_j \mathcal{P}_e\right) \hat{H'}_{at}^{-1} \left(\tilde{E}_i\mathcal{P}_e d_i \mathcal{P}_g + {\color{red}{\tilde{E}_i^*\mathcal{P}_g d_i \mathcal{P}_e}}\right) \mathcal{P}_g~.
\end{aligned} \end{equation}
显然,红色的两项包含诸如 $\mathcal{P}_e\mathcal{P}_g,\ \mathcal{P}_g\mathcal{P}_e$ 这种($\tilde{E}$ 这种外场在这时候和他们都没有对易关系)的,显然 $=0$,所以最后我们有对基态的等效 Hamiltonian
\begin{equation}
\hat{H}_{\text{eff}} = -\frac{1}{4} \mathcal{P}_g \sum_j \tilde{E}_j^*\mathcal{P}_g d_j \mathcal{P}_e \hat{H'}_{at}^{-1} \sum_i \tilde{E}_i\mathcal{P}_e d_i \mathcal{P}_g \mathcal{P}_g ~.
\end{equation}
或者,利用我们刚刚定义的二阶矩阵,我们有
\begin{equation}
\hat{H}_{\text{eff}} = -\frac{1}{4}\sum_{i,j} \tilde{E}_i^* \mathcal{D}_{ij} \tilde{E}_j~.
\end{equation}
可以把这个 $\mathcal{D}_{ij}$ 拆成三个部分:表示 trace 的各项同性矩阵 $\mathcal{D}_{ij}^0 = \frac{1}{3}Tr(\mathcal{D})\delta_{ij}$,全反对称的 $\mathcal{D}_{ij}^1 = \frac{1}{2}(\mathcal{D}_{ij} - \mathcal{D}_{ji})$,和全对称无 trace 的 $\mathcal{D}_{ij}^2 = \frac{1}{2}(\mathcal{D}_{ij} + \mathcal{D}_{ji}) - \mathcal{D}_{ij}^0$,于是
\begin{equation}
\mathcal{D}_{ij} = \mathcal{D}_{ij}^0 + \mathcal{D}_{ij}^1 + \mathcal{D}_{ij}^2~.
\end{equation}
我们接下来分析一下这种效应带来的 splitting,作为我们对于原子—光相互作用的结束。
$ \boldsymbol{\mathbf{1}} $. 极端情况下,可以忽略精细结构,也就是说 $A_f = 0$。这时候 $\mathcal{D}_{ij}$ 就不再是一个很复杂的算符,而是简单地
\begin{equation}
\mathcal{D}_{ij} = \frac{1}{\Delta_e}\mathcal{P}_g d_i d_j \mathcal{P}_g~.
\end{equation}
主要到这里两个到基态的投影算符使得中间的位置算符 $d_j$ 并没有明显的极化效应,所以 $\mathcal{D}_{ij} \propto \delta_{ij}$,$\mathcal{D}_{ij} ^1 = \mathcal{D}_{ij} ^2 = 0$。
而
\begin{equation}
\mathcal{D}_{ij}^0 = \frac{1}{3\Delta_e} \mathcal{P}_g d_j \mathcal{P}_e \mathcal{P}_e d_j \mathcal{P}_g \delta_{ij}= \frac{1}{3\Delta_e} |\mathcal{P}_g d_j \mathcal{P}_e|^2\delta_{ij}\overset{def}{\equiv} -4u_s \delta_{ij}~,
\end{equation}
其中,很显然的可以得到
\begin{equation}
u_s = -\frac{1}{12\Delta_e} |\langle l=0|{ \boldsymbol{\mathbf{d}} }|l = 1\rangle|^2~.
\end{equation}
因此,有效 Hamiltonian 为
\begin{equation}
\hat{H}_{\text{eff}} = u_s { \boldsymbol{\mathbf{E}} }^2~.
\end{equation}
这说明什么呢?这说明没有精细结构的话,光是没有办法改变电子的自旋的(Hamiltonian 里面没有包含自旋与其他参数耦合的项);而且,这种作用并不依赖光的偏振,而仅仅和光的强度有关(${ \boldsymbol{\mathbf{E}} }^2$);利用这点可以很好的进行实验上的光陷阱,从而捕捉原子;而 $\Delta_e$ 实际上与原子的速度有关(Doppler 效应),于是说给激光制冷提供了一个实验的理论指导。
{$ \boldsymbol{\mathbf{2}} $. }考虑精细结构(当然很小的精细结构)的时候的能级分裂
注意到,
\begin{equation}
{\hat H}^{-1} \equiv ({\hat H}_0+\hat{V})^{-1} = {\hat H}_0^{-1} - {\hat H}_0^{-1}\hat{V} {\hat H}^{-1}~,
\end{equation}
我们可以得到
\begin{equation}
\hat{H}_{at} = \frac{1}{\Delta_e}\mathcal{P}_e-\frac{1}{\Delta_e}\frac{A_f}{\hbar^2}{ \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} }\hat{H}_{at}^{-1} ~.
\end{equation}
从而,我们可以分出来和之前一样的 $\mathcal{D}_{ij}$ 部分,和精细结构带来的效应
\begin{equation}
\mathcal{D}_{ij} = \mathcal{P}_g d_i \frac{1}{\Delta_e} d_j \mathcal{P}_g - \alpha \mathcal{P}_g d_i { \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} }d_j\mathcal{P}_g,\quad \alpha \equiv A_f/(\hbar^2\Delta_e)~.
\end{equation}
角动量算符和位置算符有着明显的对易关系:
\begin{equation}
[L_i,d_j] = \mathrm{i} \hbar\epsilon_{ijk}d_k~,
\end{equation}
因此
\begin{equation}
d_i { \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} }d_j = { \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} }d_id_j + [{ \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} }, d_i]d_j~.
\end{equation}
第一项很显然等于 0,因为这是作用在基态上的,而基态的话 $L=0, j = s, { \boldsymbol{\mathbf{L}} \cdot \boldsymbol{\mathbf{S}} } = j(j+1) - s(s+1) = 0$,因此我们有
\begin{equation}
\mathcal{D}_{ij} = -4u_s\delta_{ij} - \mathrm{i} \alpha\hbar\epsilon_{ilm} S_l \mathcal{D}_{mj}~.
\end{equation}
做一级近似,也就是把上面式子的第二项中 $\mathcal{D}_{mj} \sim -4u_s\delta_{ij}$,于是
\begin{equation}
\mathcal{D}_{ij} = -4u_s\delta_{ij} - 4 \mathrm{i} u_s\alpha\hbar\epsilon_{ijl} S_l~.
\end{equation}
注意到,这里面,第一项对能量的贡献是量级 $1/\Delta_e$ 的,而第二项是 $1/\Delta_e^2$。热效应同样也是 $1/\Delta_e^2$,于是没办法在保持这种相互作用的程度而减小热效应。
化简可以得到
\begin{equation}
\hat{H}_{\text{eff}} = u_s|{ \boldsymbol{\mathbf{E}} }|^2 + \mathrm{i} \alpha\hbar u_s ({ \boldsymbol{\mathbf{E}} ^*\times \boldsymbol{\mathbf{E}} )\cdot S}~.
\end{equation}
可以注意到,这样的光会使得自旋的极化。例如,圆偏振,${ \boldsymbol{\mathbf{E}} } = E_0 ({ \boldsymbol{\mathbf{e}} }_x + \mathrm{i} { \boldsymbol{\mathbf{e}} }_y)$,我们会发现
\begin{equation}
{ \boldsymbol{\mathbf{E}} ^*\times E} = 2 \mathrm{i} E_0^2{ \boldsymbol{\mathbf{e}} }_z~.
\end{equation}
不难想象,这在我们将来操作冷原子的时候有很好的应用潜力。
1. ^ 注意:确实发现算错了,但是懒得改,领会精神 orz
2. ^ 实际上这就类似相互作用绘景里面常用的样子给反过来而已
\begin{equation}
U_I = \mathrm{e} ^{ \mathrm{i} \hat{H}_0t/\hbar} = \mathrm{e} ^{ \mathrm{i} \omega_e t\mathcal{P}_e}~.
\end{equation}
适用条件:
- 场几乎共振,能级差 $E_e \sim \hbar \omega$
- 场很弱,具体的话要满足 $E_j d \ll \hbar\omega$
4. ^ 注意:这里我的这个 note 写的比较乱,但是我觉得可以阅读;我也懒得改了。
5. ^ Fa Wang, Summary of Lecture 6: perturbation theory, laserroger: Site Part C, 2nd-order perturbation
6. ^ 这里可以通过这种办法检验:
\begin{equation}
({\hat H}_0^{-1} - {\hat H}_0^{-1}\hat{V} {\hat H}^{-1}) \hat{H} = 1 + {\hat H}_0^{-1} \hat{V} - {\hat H}_0^{-1}\hat{V} = 1~.
\end{equation}
致读者: 小时百科一直以来坚持所有内容免费,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 10 元,我们一个星期内就能脱离亏损, 并保证在接下来的一整年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。