Python 简介与安装

贡献者： addis; 落羽清玄; shizy0808

• 子节 1 Python 简介
• 子节 2 Python 安装

1. Python 简介

1.1.Python 是什么？

• Python 是一门流行的编程语言。由荷兰数学和计算机科学研究学会的吉多·范罗苏姆于 1990 年代初设计。
• Python 是一门解释型编程语言：这意味着开发过程中没有了编译这个环节。类似于 PHP 和 Perl 语言。
• Python 是一门交互式编程语言：这意味着，您可以在一个 Python 提示符 >>> 后直接执行代码。
• Python 是一门面向对象的语言: 这意味着 Python 支持面向对象的风格或代码封装在对象的编程技术。

1.2.Python 可以做什么？

• Web 开发：可以在服务器上使用 Python 来创建 Web 应用程序。
• 软件开发：可用于快速原型设计，也可用于生产就绪的软件开发。
• 数学运算：Python 可用于处理大数据并执行复杂的数学运算。
• 系统脚本：可以与软件一起使用来创建工作流。

1.3.Python 有什么特点？

• 易于学习：Python 有相对较少的关键字，结构简单和一个明确定义的语法。
• 易于阅读：Python 代码定义的更清晰。
• 易于维护：Python 的成功在于它的源代码是相当容易维护的。
• 可嵌入: 你可以将 Python 嵌入到 C/C++程序，让你的程序拥有"脚本化"的能力。
• 广泛的标准库：Python 的最大的优势之一是丰富的库，且跨平台在 UNIX，Windows 和 Mac 兼容很好。
• 可扩展：如果你需要一段运行很快的关键代码，或者是想要编写一些不愿开放的算法，你可以使用 C 或 C++完成那部分程序，然后从你的 Python 程序中调用。

2. Python 安装

　　 Python 已经能够工作在不同平台上。您需要下载适用于您使用平台的二进制代码，然后安装 Python。如果您平台的二进制代码是不可用的，你需要使用 C 编译器手动编译源代码。编译的源代码，功能上有更多的选择性，为 Python 安装提供了更多的灵活性。不过需要注意：太高版本的 Python 部分库是无法安装的（推荐 3.8.6）

2.1.Window 平台安装 Python:

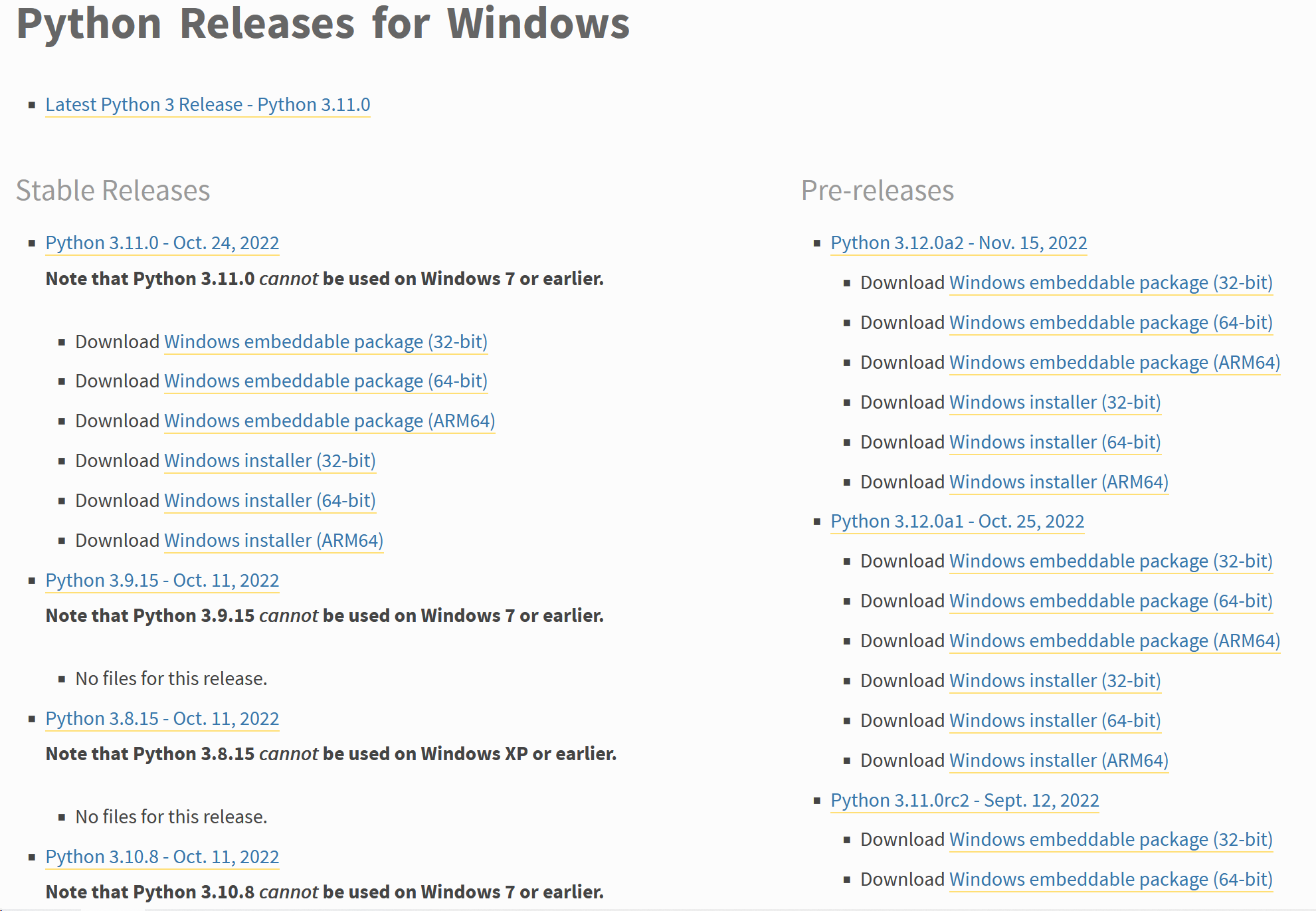
　　 访问 Python 官网关于 Windows 下载，一般就下载 Windows installer，其中 “Stable Releases” 是指稳定版本，推荐下载。

　　 安装以后在开始菜单中搜索程序名如 Python 3.8 (64-bit)，点击后即可打开 Python 命令行。安装包也会自动安装 pip3，可以在 Powershell 或者 cmd 中输入 pip3 --version 查看。

2.2.MAC 平台安装 Python:

　　 MAC 系统都自带有 Python2.7 环境，你可以在链接 Python 官网关于 mac 下载 上下载最新版安装 Python 3.x。你也可以参考源码安装的方式来安装。

2.3.Unix 和 Linux 平台安装 Python:

　　 你可以访问 Python 官网关于 Linux 下载,选择适用于 Unix/Linux 的源码压缩包。

　　 也可以直接用命令行下载

wget https://www.python.org/ftp/python/3.7.6/Python-3.7.6.tgz

　　 创建安装目录（你想放哪就放哪）

mkdir -p /usr/local/python3

　　 解压

tar -zxvf Python-3.7.6.tgz

　　 编译安装

# gcc 环境、zlib 库和 readline-devel 包
yum -y install gcc
yum -y install zlib*
yum install readline-devel
# 配置
cd Python-3.7.6
./configure --prefix=/usr/local/python3
# 编译安装
make && make install

　　 建立软链接

ln -s /usr/local/python3/bin/python3.7 /usr/bin/python3
ln -s /usr/local/python3/bin/pip3.7 /usr/bin/pip3

　　 测试安装

# 返回 Python 3.7.6（版本）
python3 --version
# 命令行输出
python3
......
print("你好")