贡献者: addis; jiangnan
1. 二维分布函数
我们以打靶为例来引入二元概率分布函数,以及在直角坐标系和极坐标系中如何分析各种平均值。我们在靶上建立 $x$-$y$ 直角坐标系,类比一维概率分布函数的定义,二维概率分布可以用一个二元函数表示为 $f(x, y)$,也叫概率密度(probability density)。子弹落在一个长方形区域内(令 $x \in [x_1, x_2]$,$y \in [y_1, y_2]$)的概率可以用二重积分表示
\begin{equation}
P = \int_{y_1}^{y_2} \int_{x_1}^{x_2} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
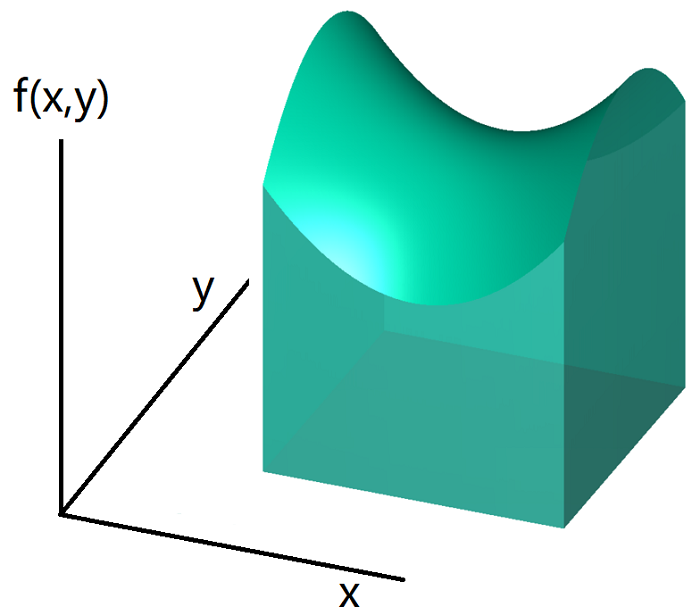
从几何上理解,$f(x, y)$ 可以看作一张三维空间中的曲面,而这个二重积分则表示曲面和 $x$-$y$ 平面之间的一个体积(
图 1 )。
图 1:$f(x, y)$ 曲面下的体积
类比一维情况,概率归一化条件为
\begin{equation}
\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} = 1~.
\end{equation}
由于概率的量纲是 1,$f(x, y)$ 的国际单位量纲就是 $ \,\mathrm{m^{-2}} $,即面积的倒数。
2. 平均值
类比式 10 ,离散情况下,令 $P_i$ 是 $(x_i, y_i)$ 出现的概率,函数 $g(x,y)$ 的平均值为
\begin{equation}
\left\langle g \right\rangle = \sum_{i=1}^N g(x_i, y_i) P_i~.
\end{equation}
拓展到连续的情况,类比
式 11 ,$g(x, y)$ 的平均值可以定义为
\begin{equation}
\left\langle g \right\rangle = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x, y) f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
例如位置矢量的 $x$ 和 $y$ 分量平均值分别为
\begin{equation}
\left\langle x \right\rangle = \iint x f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~,
\end{equation}
\begin{equation}
\left\langle y \right\rangle = \iint y f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
以上两式也可以用位置矢量 $ \boldsymbol{\mathbf{r}} $ 表示为(这时 $ \boldsymbol{\mathbf{g}} $ 的函数值是矢量)
\begin{equation}
\left\langle \boldsymbol{\mathbf{r}} \right\rangle = \iint \boldsymbol{\mathbf{r}} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~,
\end{equation}
点 $(x,y)$ 到原点距离的距离 $r$ 的平均值
\begin{equation}
\left\langle r \right\rangle = \iint \sqrt{x^2 + y^2} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
注意区分该式和
式 7 式的意义,平均位置和平均距离是两个不同的概念:如果 $f(x, y)$ 是关于原点中心对称的函数,则平均位置为 $(0, 0)$,而平均距离不为零。
距离平方 $r^2$ 的平均值
\begin{equation}
\left\langle r^2 \right\rangle = \iint (x^2 + y^2) f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
3. 概率分布的极坐标表示
除了直角坐标系外,我们也可以使用极坐标 表示分布函数,记为1 $f(r, \theta)$,那么概率归一化条件变为
\begin{equation}
\int_0^\infty \int_{0}^{2\pi} f(r, \theta)\,\, r \,\mathrm{d}{\theta} \,\mathrm{d}{r} = 1~,
\end{equation}
函数 $g(r, \theta)$ 的平均值变为
\begin{equation}
\left\langle g \right\rangle = \int_0^\infty \int_{0}^{2\pi} g(r, \theta) f(r, \theta)\,\, r \,\mathrm{d}{\theta} \,\mathrm{d}{r} ~.
\end{equation}
例如
式 9 变为
\begin{equation}
\left\langle r^2 \right\rangle = \int_0^\infty \int_{0}^{2\pi} r^2 f(r, \theta)\,\, r \,\mathrm{d}{\theta} \,\mathrm{d}{r}
= \int_0^\infty \int_{0}^{2\pi} r^3 f(r, \theta) \,\mathrm{d}{\theta} \,\mathrm{d}{r} ~.
\end{equation}
4. 圆对称分布
继续打靶的例子,我们接下来讨论圆对称的概率分布(在三维情况下叫做球对称),即 $f(r, \theta)$ 的值只和 $r$ 有关而与 $\theta$ 无关的情况。为了书写方便可记 $f(r) \equiv f(r, \theta)$。归一化条件式 10 化简为(先完成关于 $\theta$ 积分得 $2\pi$)
\begin{equation}
2\pi \int_0^\infty r f(r) \,\mathrm{d}{r} = 1~.
\end{equation}
一个容易混淆的概念是,$f(r)$ 并不是变量 $r$ 的概率分布函数。也就是说 $\int_a^b f(r) \,\mathrm{d}{r} $ 并不是子弹落在圆环 $r \in [a, b]$ 内的概率。若将 $r$ 的概率分布函数记为 $F(r)$,子弹落在圆环中的概率应该是
\begin{equation}
P_{ab} = \int_a^b F(r) \,\mathrm{d}{r} = \int_a^b 2\pi r f(r) \,\mathrm{d}{r} ~.
\end{equation}
由于两个定积分在任何区间都相等,两个被积函数必须相等,即
\begin{equation}
F(r) = 2\pi r f(r)~.
\end{equation}
这时以上的平均值也可以得到进一步化简,例如
式 12 变为
\begin{equation}
\left\langle r^2 \right\rangle = \int_0^\infty r^2 F(r) \,\mathrm{d}{r}
= 2\pi \int_0^\infty r^3 f(r) \,\mathrm{d}{r} ~.
\end{equation}
5. 多随机变量的函数的分布
我们在前面已经知道定义在随机变量 X、Y 上的函数 $g(x,y)$ 的平均值 $\bar{g}$ 如何计算,但实际上如果关注每次 $g(x,y)$ 的值,我们会发现 $g(x,y)$ 也满足一定的概率分布,那如何求解这个概率分布呢?我们以二元随机变量的几个例子为例说明。首先我们引入分布函数这个概念
定义 1 分布函数与边缘分布函数
对于一个随机变量 X,我们定义分布函数为 $F(\alpha)=P(x\leq \alpha) = \int_{-\infty}^{\alpha} f(x)dx$。对于一个二维连续随机变量(X,Y),其边缘分布函数有两个,X 的边缘分布函数 $F_X(x)$ 与 Y 的边缘分布函数 $F_Y(y)$,定义为
\begin{align}
F_X(x) = \int_{-\infty}^{+\infty} dy^\prime \int_{-\infty}^{x} dx^\prime f(x^\prime,y^\prime)\\~
F_Y(y) = \int_{-\infty}^{+\infty} dx^\prime \int_{-\infty}^y dy^\prime f(x^\prime,y^\prime)~
\end{align}
类似地我们可以定义边缘概率密度函数 $f_X(x) = \frac{dF_X(x)}{dx}$,$f_Y(y) = \frac{dF_Y(y)}{dy}$。
例 1
我们定义随机变量 $Z=X+Y$,求 $Z$ 的分布的概率密度函数,这时我们要先去求 $Z$ 的分布函数,$F_Z(\alpha)=P(z\leq \alpha) = P(x+y\leq \alpha)$,而 $P(x+y\leq \alpha) = \int_{-\infty}^{+\infty}dx \int_{-\infty}^{\alpha-x} dy f(x,y)$,当给定二元分布函数的概率密度 $f(x,y)$ 后,$F_Z(\alpha)$ 即可积分算出。继而通过 $f_Z(z) = \frac{d F_Z(z)}{dz}$ 即可求得。
1. ^ 在数学上,该式两边是两个不同的二元函数,应该使用不同的函数名如 $g(r, \theta) = f(x, y)$,但在一些物理教材中,我们有时为了方便不区分函数名,直接把 $g(r, \theta)$ 写成 $f(r, \theta)$。
致读者: 小时百科一直以来坚持所有内容免费,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 10 元,我们一个星期内就能脱离亏损, 并保证在接下来的一整年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。